5.3 轴对称与坐标变化 第2课时 课件(共12张PPT)
文档属性
| 名称 | 5.3 轴对称与坐标变化 第2课时 课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
点P(a,b)关于X 轴对称的点的坐标是:
关于Y 轴对称的点的坐标是:
关于原点对称的点的坐标是:
(a,-b)
(-a,b)
(-a,-b)
学习目标
1.在同一直角坐标系,感受图形上点的横、纵坐标的变化与图形的轴对称之间的关系.
2.经历图形的坐标变化与图形的轴对称之间的关系的探索过程,发展形象思维能力和数形结合意识.
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
对应点 的坐标又有什么特点?
纵坐标相同,横坐标互为相反数
其它对应的点也有这个特点吗?
探 究
同样具有
(2,6)
(-2,6)
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
在平面直角坐标系中依次连接下列各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0),你得到一个什么图案?
y
x
两个图形关于y轴对称
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
一条小鱼
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
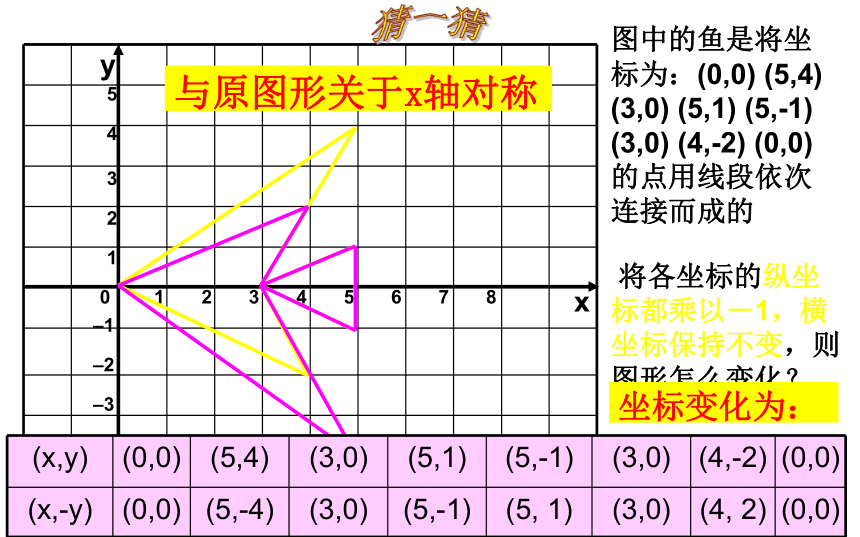
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
y
x
与原图形关于x轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
在坐标系中作一个图形关于x轴或y轴的对称图形,需作
出这个图形的顶点关于x轴或y轴的_______,然后_____连接这
些_______.
将一个图形各顶点的横坐标乘以-1,纵坐标不变,那么得到的
图形与原图形关于__轴对称.
将一个图形各顶点的纵坐标乘以-1,横坐标不变,那么得到的
图形与原图形关于__轴对称.
对称点
顺次
对称点
y
x
在坐标系中作一个图形关于x轴或y轴的对称图形
【例2】在如图所示的坐标系中,作出四边形ABCD关于x轴对称的四边形A′B′C′D′.
【解题探究】1.关于x轴对称的两个点的坐标有什么关系?
提示:横坐标相同,纵坐标互为相反数.
2.在坐标系中,作出四边形A′B′C′D′的关键是什么?
提示:确定A′,B′,C′,D′的位置.
3.A′,B′,C′,D′的坐标分别为________,_______,
_______,________.
(-2,1)
(1,3)
(4,1)
(1,-1)
4.在坐标系中描出A′,B′,C′和D′四个点,并顺次连接这四个点,得四边形A′B′C′D′即为四边形ABCD关于x轴的对称图形.作图如图所示:
【规律总结】
在坐标系中作轴对称图形的“四步法”
1.确定原图形中各个顶点的坐标.
2.根据对称点的坐标关系确定对称点的坐标;
3.在坐标系中描出各个对称点.
4.顺次连接这些对称点,即得原图形的轴对称图形.
点P(a,b)关于X 轴对称的点的坐标是:
关于Y 轴对称的点的坐标是:
关于原点对称的点的坐标是:
(a,-b)
(-a,b)
(-a,-b)
学习目标
1.在同一直角坐标系,感受图形上点的横、纵坐标的变化与图形的轴对称之间的关系.
2.经历图形的坐标变化与图形的轴对称之间的关系的探索过程,发展形象思维能力和数形结合意识.
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
对应点 的坐标又有什么特点?
纵坐标相同,横坐标互为相反数
其它对应的点也有这个特点吗?
探 究
同样具有
(2,6)
(-2,6)
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
在平面直角坐标系中依次连接下列各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0),你得到一个什么图案?
y
x
两个图形关于y轴对称
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
一条小鱼
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
y
x
与原图形关于x轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
在坐标系中作一个图形关于x轴或y轴的对称图形,需作
出这个图形的顶点关于x轴或y轴的_______,然后_____连接这
些_______.
将一个图形各顶点的横坐标乘以-1,纵坐标不变,那么得到的
图形与原图形关于__轴对称.
将一个图形各顶点的纵坐标乘以-1,横坐标不变,那么得到的
图形与原图形关于__轴对称.
对称点
顺次
对称点
y
x
在坐标系中作一个图形关于x轴或y轴的对称图形
【例2】在如图所示的坐标系中,作出四边形ABCD关于x轴对称的四边形A′B′C′D′.
【解题探究】1.关于x轴对称的两个点的坐标有什么关系?
提示:横坐标相同,纵坐标互为相反数.
2.在坐标系中,作出四边形A′B′C′D′的关键是什么?
提示:确定A′,B′,C′,D′的位置.
3.A′,B′,C′,D′的坐标分别为________,_______,
_______,________.
(-2,1)
(1,3)
(4,1)
(1,-1)
4.在坐标系中描出A′,B′,C′和D′四个点,并顺次连接这四个点,得四边形A′B′C′D′即为四边形ABCD关于x轴的对称图形.作图如图所示:
【规律总结】
在坐标系中作轴对称图形的“四步法”
1.确定原图形中各个顶点的坐标.
2.根据对称点的坐标关系确定对称点的坐标;
3.在坐标系中描出各个对称点.
4.顺次连接这些对称点,即得原图形的轴对称图形.
