第二十章:数据的分析练习题2021-2022学年内蒙古八年级下学期人教版数学期末试题选编 含解析
文档属性
| 名称 | 第二十章:数据的分析练习题2021-2022学年内蒙古八年级下学期人教版数学期末试题选编 含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 549.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 10:46:37 | ||
图片预览


文档简介
第二十章:数据的分析 练习题
一、单选题
1.(2022春·内蒙古鄂尔多斯·八年级统考期末)某校“啦啦操”兴趣小组共有50名学生,她们的年龄分布如下表:
年龄/岁 12 13 14 15
人数 5 23 ■ ■
由于表格污损,14岁、15岁人数看不清,则下列关于年龄的统计量可以确定的是( ).
A.平均数、众数 B.众数、中位数 C.平均数、中位数 D.中位数、方差
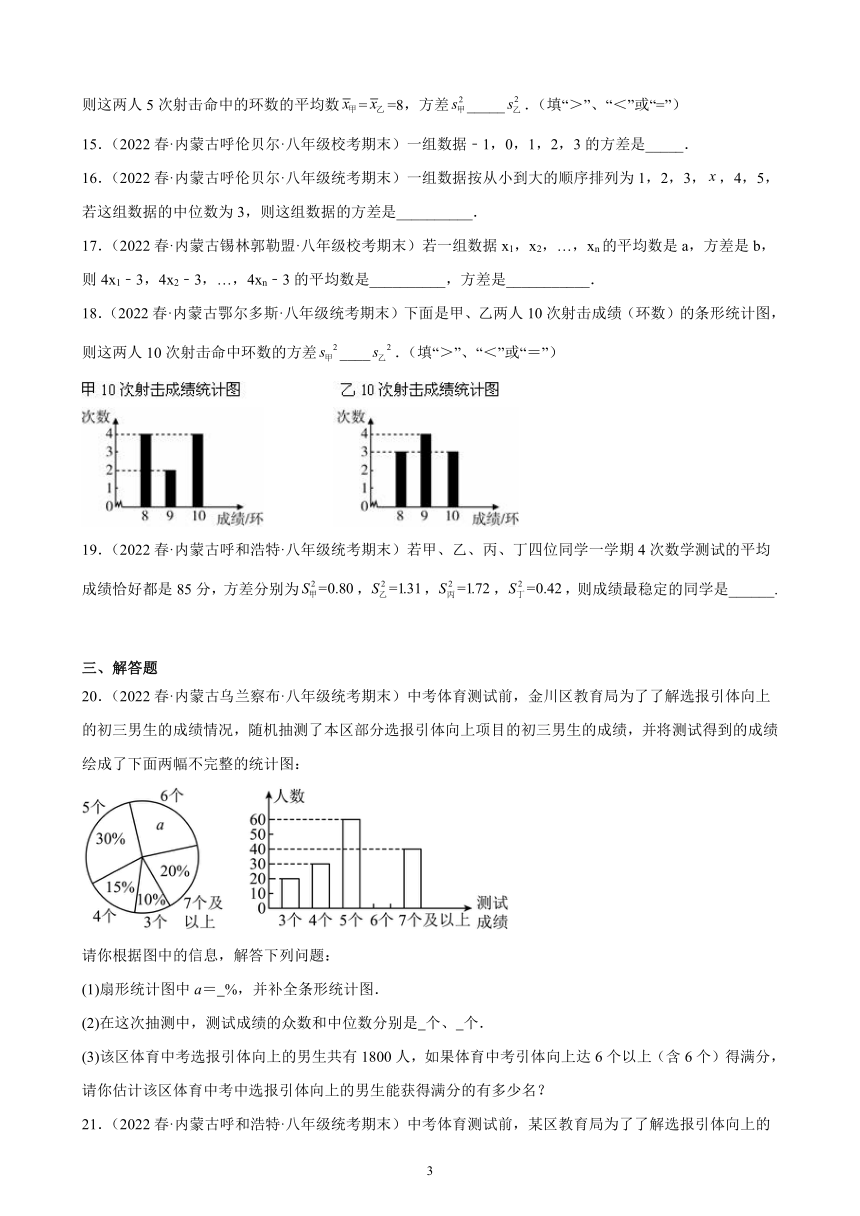
2.(2022春·内蒙古呼伦贝尔·八年级统考期末)某校七年级1班50名同学在“森林草原防灭火”知识竞赛中的成绩如表所示:
成绩 60 70 80 90 100
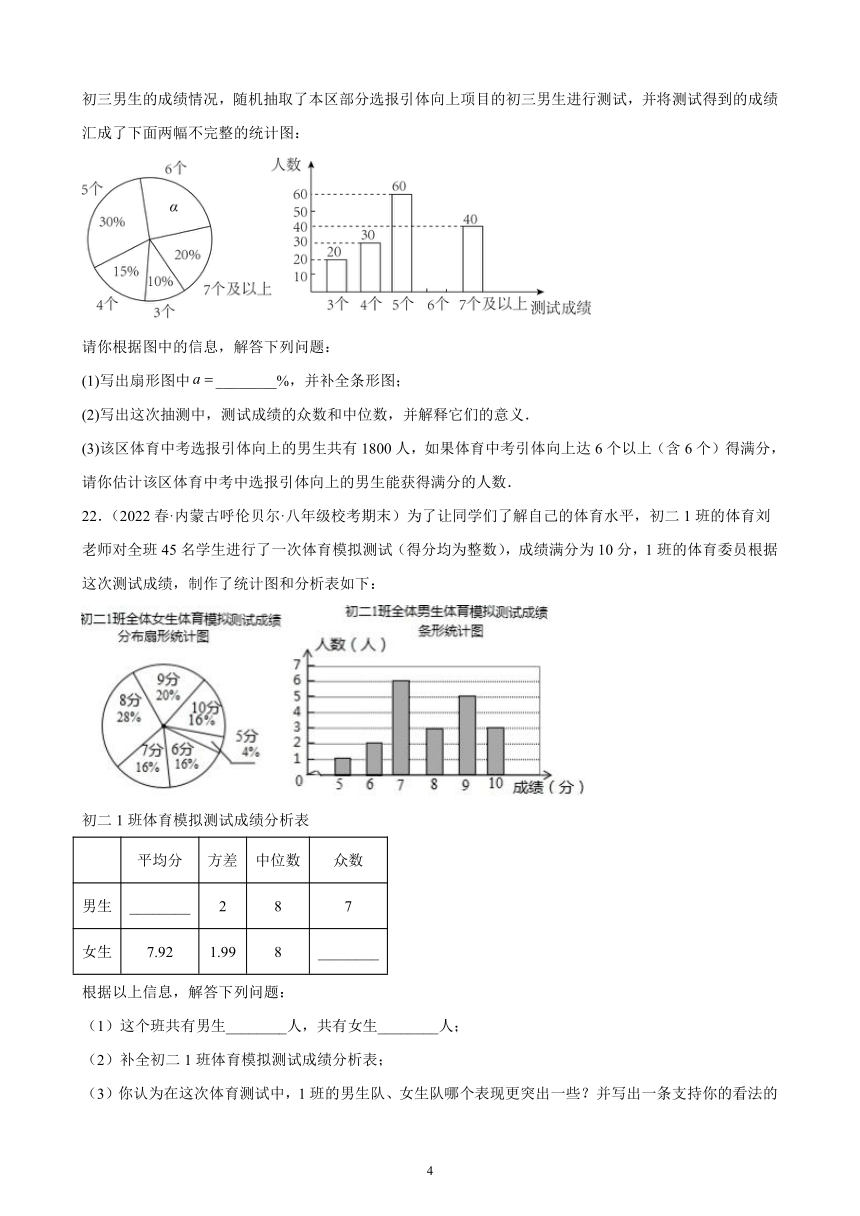
人数 3 9 13 16 9
则这个班学生成绩的众数、中位数分别是( )
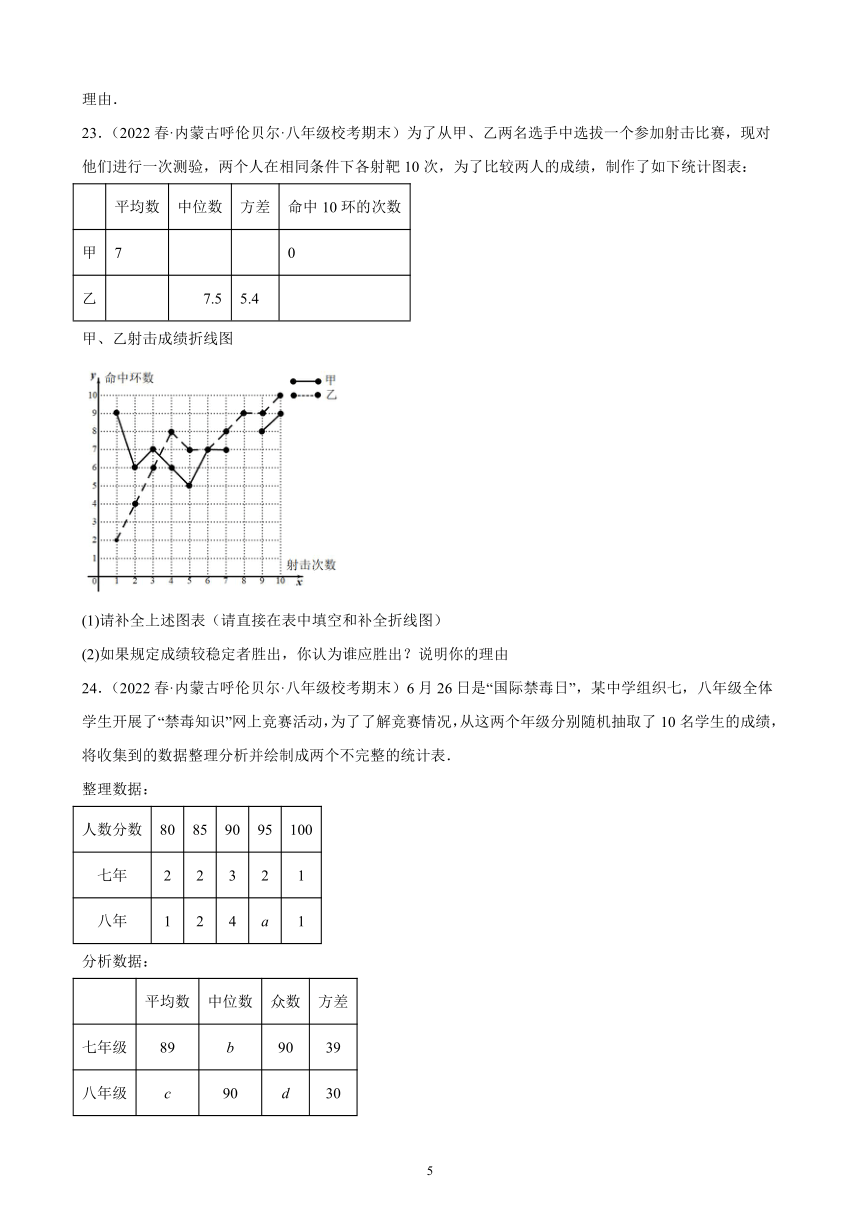
A.90,80 B.16,85 C.16,24.5 D.90,85
3.(2022春·内蒙古通辽·八年级校考期末)如果你和其余6人进入了八年级速算比赛的总决赛,你想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的( )
A.平均数 B.众数 C.中位数 D.方差
4.(2022春·内蒙古呼伦贝尔·八年级校考期末)在暑假到来之前,某机构向八年级学生推荐了A,B,C三条游学线路,现对全级学生喜欢哪一条游学线路作调查,以决定最终的游学线路,下面的统计量中最值得关注的是( )
A.方差 B.平均数 C.中位数 D.众数
5.(2022春·内蒙古呼伦贝尔·八年级校考期末)某商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如表所示
型号 22 22.5 23 23.5 24 24.5 25
数量(双) 2 6 11 15 7 3 4
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A.平均数 B.方差 C.中位数 D.众数
6.(2022春·内蒙古巴彦淖尔·八年级统考期末)一组数据的方差可以用式子表示,则式子中的数字50所表示的意义是( )
A.这组数据的个数 B.这组数据的平均数
C.这组数据的众数 D.这组数据的中位数
7.(2022春·内蒙古呼伦贝尔·八年级校考期末)已知一组数据的方差计算公式为:,由公式提供的信息,则下列说法错误的是( )
A.中位数是3 B.众数是3 C.平均数是3.5 D.方差是0.5
8.(2022春·内蒙古锡林郭勒盟·八年级校考期末)小明同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数 B.方差 C.中位数 D.众数
9.(2022春·内蒙古乌兰察布·八年级统考期末)某校举行课间操比赛,甲、乙两个班各选出20名学生参加比赛,两个班参赛学生的平均身高都为1.65m,其方差分别是S甲2=3.8,S乙2=3.4,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
二、填空题
10.(2022春·内蒙古呼伦贝尔·八年级校考期末)某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=7∶3的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是___________分.
11.(2022春·内蒙古呼伦贝尔·八年级校考期末)已知一组数据x1,x2,x3,x4,x5的平均数是2,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是_____.
12.(2022春·内蒙古巴彦淖尔·八年级统考期末)若一组数据2,3,x,5,7的众数为7,则这组数据的中位数为_________.
13.(2022春·内蒙古乌兰察布·八年级统考期末)已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是______.
14.(2022春·内蒙古呼伦贝尔·八年级统考期末)甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
15.(2022春·内蒙古呼伦贝尔·八年级校考期末)一组数据﹣1,0,1,2,3的方差是_____.
16.(2022春·内蒙古呼伦贝尔·八年级统考期末)一组数据按从小到大的顺序排列为1,2,3,,4,5,若这组数据的中位数为3,则这组数据的方差是__________.
17.(2022春·内蒙古锡林郭勒盟·八年级校考期末)若一组数据x1,x2,…,xn的平均数是a,方差是b,则4x1﹣3,4x2﹣3,…,4xn﹣3的平均数是__________,方差是___________.
18.(2022春·内蒙古鄂尔多斯·八年级统考期末)下面是甲、乙两人10次射击成绩(环数)的条形统计图,则这两人10次射击命中环数的方差____.(填“>”、“<”或“=”)
19.(2022春·内蒙古呼和浩特·八年级统考期末)若甲、乙、丙、丁四位同学一学期4次数学测试的平均成绩恰好都是85分,方差分别为,,,,则成绩最稳定的同学是______.
三、解答题
20.(2022春·内蒙古乌兰察布·八年级统考期末)中考体育测试前,金川区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)扇形统计图中a= %,并补全条形统计图.
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、 个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
21.(2022春·内蒙古呼和浩特·八年级统考期末)中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生进行测试,并将测试得到的成绩汇成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中________%,并补全条形图;
(2)写出这次抽测中,测试成绩的众数和中位数,并解释它们的意义.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的人数.
22.(2022春·内蒙古呼伦贝尔·八年级校考期末)为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
初二1班体育模拟测试成绩分析表
平均分 方差 中位数 众数
男生 ________ 2 8 7
女生 7.92 1.99 8 ________
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由.
23.(2022春·内蒙古呼伦贝尔·八年级校考期末)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 7.5 5.4
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由
24.(2022春·内蒙古呼伦贝尔·八年级校考期末)6月26日是“国际禁毒日”,某中学组织七,八年级全体学生开展了“禁毒知识”网上竞赛活动,为了了解竞赛情况,从这两个年级分别随机抽取了10名学生的成绩,将收集到的数据整理分析并绘制成两个不完整的统计表.
整理数据:
人数分数 80 85 90 95 100
七年 2 2 3 2 1
八年 1 2 4 a 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 c 90 d 30
(1)______;______;______;______;
(2)该校七、八年级学生共有600人,本次竞赛成绩不低于90分为“优秀”估计这两个年级达到成绩“优秀”的学生共有多少人?
25.(2022春·内蒙古鄂尔多斯·八年级统考期末)某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)___________,___________;
(2)从方差的角度看,___________种西瓜的得分较稳定(填“甲”或“乙”);
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
26.(2022春·内蒙古呼伦贝尔·八年级校考期末)学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明第2次的成绩为: 秒;
(2)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
参考答案:
1.B
【分析】根据众数、中位数的定义进行判断即可.
【详解】解:由题意可知,“啦啦操”兴趣小组共有50人,中位数是从小到大排列后处在第25、26位学生年龄的平均数,而12岁的学生有5人,13岁的学生有23人,因此从小到大排列后,处在第25、26位的两个学生都是13岁,因此中位数是13岁,不受14岁、15岁人数的影响;因为13岁的学生有23人,而12岁的学生有5人,14岁、15岁的学生共有22人,因此众数是13岁.
故选:B.
【点睛】本题主要考查了中位数和众数的知识,正确掌握众数和中位数的定义是解题的关键.
2.D
【分析】根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按从小到大依次排列,处于中间位置的两个数的平均数即为中位数.
【详解】解:90分的有16人,人数最多,故众数为90分;
处于中间位置的数为第25、26两个数,为80和90,
∴中位数为=85分.
故选:D.
【点睛】本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
3.C
【分析】根据题意可得:由中位数的概念,可知7人成绩的中位数是第4名的成绩.参赛选手要想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】解:由于总共有7个人,第4位选手的成绩是中位数,要判断是否进入前3名,
故应知道自己的成绩和中位数.
故选:C.
【点睛】本题考查的是中位数的含义,以及利用中位数作判断,理解中位数的含义是解本题的关键.
4.D
【详解】由于众数是数据中出现次数最多的数,
故全级学生喜欢的游学线路最值得关注的应该是统计调查数据的众数,
故选D.
5.D
【分析】根据众数的定义:一组数据中出现次数最多的数值,即可得解.
【详解】根据题意,销量最大,即为众数,故答案为D.
【点睛】此题主要考查对众数的理解运用,熟练掌握,即可解题.
6.B
【分析】根据方差公式的特点进行解答即可.
【详解】解:方差的定义:一般地设n个数据,x1,x2,…x的平均数为,则方差S2[(x1)2+(x2)2+…+(x)2],
所以50是这组数据的平均数.
故答案选:B
【点睛】此题考查了方差,熟练掌握方差的计算公式是解题的关键,一般地设n个数据,x1,x2,…x的平均数为,则方差S2[(x1)2+(x2)2+…+(x)2].
7.C
【分析】根据已知的方差计算公式得出这组数据为2、3、3、4,再根据中位数,众数,平均数以及方差的概念求解即可.
【详解】由题意可知这组数据为2、3、3、4、所以中位数为,故选项A不符题意.
众数为3,故选B不符合题意.
平均数为,故选项C符合题意.
方差为,故选项D不符题意,
故选C.
【点睛】本题主要考查方差,样本容量,中位数,众数及平均数的定义,掌握方差的计算公式是解题的关键.
8.C
【分析】利用平均数、中位数、方差和标准差的定义对各选项进行判断.
【详解】解:这组数据的平均数、方差和标准差都与第5个数有关,而这组数据的中位数为36与46的平均数,与第5个数无关.
故选:C.
【点睛】本题考查了方差:它也描述了数据对平均数的离散程度.也考查了中位数、平均数和众数的概念,解题的关键是熟练掌握平均数、中位数、方差和标准差的定义.
9.B
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定
【详解】S甲2=3.8,S乙2=3.4,
∴S甲2>S乙2,
∴参赛学生身高比较整齐的班级是乙班,
故选B.
【点睛】此题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
10.87
【分析】根据加权平均数的求法,求出该竞聘教师的最后成绩是多少即可.
【详解】解:∵(90×7+80×3)÷(7+3)
=870÷10
=87(分)
∴该竞聘教师的最后成绩是87分.
故答案为:87.
【点睛】此题主要考查了加权平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.
11.4
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.先求数据x1,x2,x3,x4,x5的和,然后再用平均数的定义求新数据的平均数.
【详解】一组数据x1,x2,x3,x4,x5的平均数是2,有(x1+x2+x3+x4+x5)=2,
那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数是(3x1-2+3x2-2+3x3-2+3x4-2+3x5-2)=4.
故答案是:4.
【点睛】考查的是样本平均数的求法及运用,解题关键是记熟公式:.
12.5
【分析】根据众数的定义可得x的值,再依据中位数的定义即可得答案.
【详解】解:∵数据2,3,x,5,7的众数为7,
∴,
把这组数据从小到大排列为:2、3、5、7、7,
则中位数为5.
故答案为:5.
【点睛】本题考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.众数是数据中出现最多的一个数.
13.2.5
【分析】先根据众数是一组数据中出现次数最多的数据,求得x,再由中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
【详解】解:∵3与2都重复出现两次,众数是2,
∴x=2,
从小到大排列此数据为:1,2,2,2,3,3,5,7.
处在第4、5位的数分别是2,3,(2+3)÷2=2.5.
故答案为:2.5.
【点睛】本题主要考查了中位数和众数的定义,解题的关键在于能够熟练掌握中位数和众数的定义.
14.>
【分析】根据甲乙的数据利用方差的计算公式即可求解.
【详解】解:S2甲=[(7-8)2+(9 8)2+(8 8)2+(6 8)2+(10 8)2)]=2,
S2乙=[(7-8)2+(8 8)2+(9 8)2+(8 8)2+(8 8)2)]=0.4,
∴S2甲>S2乙.
故答案为:>.
【点睛】本题考查了方差的应用,解题的关键是熟练掌握方差的计算公式即可解决问题.
15.2
【详解】这组数据的平均数为:(-1+1+0+2+3)÷5=1,所以方差=[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2.
16.
【详解】试题分析:根据中位数的求法可知=3,解得x=3,因此这组数的平均数为=,所以方差为s==.
考点:数据的分析
17. 4a﹣3 16b.
【详解】∵x1、x2…xn的平均数是a,
∴(x1、x2…xn)÷n=a
∴(4x1-3,4x2-3…4xn-3)÷4=4×a-3=4a-3,
∵x1、x2…xn的方差是b,
∴4x1-3,4x2-3…4xn-3的方差是4×4×b=16b.
答案是:4a-3;16b.
【点睛】本题考查平均数和方差的变换特点,若在原来数据前乘以同一个数,平均数也乘以同一个数,而方差要乘以这个数的平方,在数据上同加或减同一个数,方差不变.
18.>
【分析】先分别求出各自的平均数,再根据方差公式求出方差,即可作出比较.
【详解】甲的平均数
则
乙的平均数
则
所以
【点睛】本题属于基础应用题,只需学生熟练掌握方差的求法,即可完成.
19.丁
【分析】根据方差越大越不稳定,方差越小越稳定解答即可.
【详解】∵1.72>1.31>0.80>0.42,
∴丁同学的成绩最稳定.
故答案为丁.
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
20.(1)25,图见解析
(2)5,5
(3)810名
【分析】(1)用1减去其他天数所占的百分比即可得到a的值,用360°乘以它所占的百分比,即可求出该扇形所对圆心角的度数;
(2)根据众数与中位数的定义求解即可;
(3)先求出样本中得满分的学生所占的百分比,再乘以1800即可.
【详解】(1)解:扇形统计图中a=1-30%-15%-10%-20%=25%,
设引体向上6个的学生有x人,由题意得
,解得x=50.
条形统计图补充如下:
故答案为:5;
(2)解:由条形图可知,引体向上5个的学生有60人,人数最多,所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,故中位数为(5+5)÷2=5.
故答案为:5,5.
(3)解:(名).
答:估计该区体育中考选报引体向上的男生能获得满分的同学有810名.
【点睛】本题考查了众数与中位数的意义.一组数据中出现次数最多的数据叫做众数;将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.也考查了条形统计图、扇形统计图与用样本估计总体.
21.(1)25,见解析
(2)众数是5,中位数是5;众数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多;中位数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多
(3)810名
【分析】(1)根据扇形统计图可以求得a的值,根据扇形统计图和条形统计图可以得到做6个的学生数,从而可以将条形图;
(2)根据众数与中位数的定义求解即可;
(3)先求出样本中得满分的学生所占的百分比,再乘以1800即可.
(1)
解:扇形统计图中,
设引体向上6个的学生有x人,
由题意得
解得.
条形统计图补充如下:
答案为:25;
(2)
解:由条形图可知,引体向上5个的学生有60人,人数最多,所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,故中位数为
众数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多;
中位数表示的意义:这次的抽样调查中,说明一半初三男生引体向上的成绩大于等于5个,另一半初三男生引体向上的成绩小于等于5个;
(3)
解:(名).
答:估计该区体育中考选报引体向上的男生能获得满分的同学有810名.
【点睛】本题为统计题,考查众数与中位数的意义.一组数据中出现次数最多的数据叫做众数;将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.也考查了条形统计图、扇形统计图与用样本估计总体.
22.(1)20、25;(2)见解析;(3)见解析
【分析】(1)由条形图可得男生总人数,总人数减去男生人数可得女生人数;
(2)根据平均数和众数定义可得;
(3)可根据众数比较得出答案.
【详解】解:(1)这个班共有男生人,共有女生人,
故答案为:20、25;
(2)甲的平均分为,女生的众数为8,
补全表格如下:
平均分 方差 中位数 众数
男生 7.9 2 8 7
女生 7.92 1.99 8 8
(3)从众数看,女生队的众数高于男生队的众数,所以女生队表现更突出.
【点睛】本题主要考查平均数、众数及条形图、扇形图,根据统计图得出解题所需数据,并熟练掌握平均数和众数的定义是解题的关键.
23.(1)见解析
(2)甲胜出,方差小,见解析
【分析】(1)分别利用中位数以及方差和平均数求法得出即可;
(2)根据(1)计算出的甲乙两人的方差,比较大小即可做出判断.
(1)
根据折线统计图得:
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:×(2+4+6+8+7+7+8+9+9+10)=7(环),
甲的射击成绩为9,6,7,6,5,7,7,?,8,9,平均数为7环,
则甲第八环成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),
所以甲的10次成绩为:9,6,7,6,5,7,7,6,8,9,
把这些数从小到大排列为5,6,6,6,7,7,7,8,9,9,
则中位数是:=7(环),
甲的方差为:;
乙命中10环的次数为1.
补统计表如下:
平均数 中位数 方差 命中10环的次数
甲 7 7 1.6 0
乙 7 7.5 5.4 1
补全折线统计图如下:
(2)
由甲的方差小于乙的方差,甲比较稳定,故甲胜出.
【点睛】此题考查了折线统计图,中位数,方差,平均数,以及统计表,掌握相关统计量的计算方法是解本题的关键.
24.(1);;;
(2)估计这两个年级达到成绩“优秀”的学生共有390人
【分析】(1)根据提供数据确定八年级95分的人数,利用众数中位数及平均数分别确定其他未知数即可.
(2)用样本的平均数估计总体的平均数即可.
【详解】(1)八年级95分的有10-1-2-4-1=2(人),故a=2,
七年级的中位数为,故b=90,
八年级的平均数为,故,
八年级中90分的最多,故,
故答案为:2,90,90,90;
(2)(人),
答:估计这两个年级达到成绩优秀的学生共有390人.
【点睛】本题考查了中位数,众数,平均数等统计基础知识,明确相关统计量表示的意义及相关计算是解题的关键.
25.(1)a=88,b=90;(2)乙;(3)见解析
【分析】(1)根据中位数、众数的意义求解即可;
(2)根据数据大小波动情况,直观可得答案;
(3)从方差、中位数、众数的比较得出答案.
【详解】解:(1)甲品种西瓜测评得分从小到大排列处在中间位置的一个数是88,所以中位数是88,即a=88,
将乙品种西瓜的测评得分出现次数最多的是90分,因此众数是90,即b=90,
故答案为:a=88,b=90;
(2)由甲、乙两种西瓜的测评得分的大小波动情况,直观可得S乙2<S甲2,
故答案为:乙;
(3)小明认为甲种西瓜的品质较好些,是因为甲的得分众数比乙的得分众数高;小军认为乙种西瓜的品质较好些,是因为乙的得分方差小和得分中位数比甲的高.
【点睛】本题考查统计表,中位数、众数、平均数,理解中位数、众数、平均数的意义和计算方法是正确解答的前提.
26.(1)13.4;
(2)13.3,13.3,0.02;
(3)选择张明参加比赛,理由见解析.
【分析】(1)根据统计图给出的数据可直接得出答案;
(2)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(3)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:根据统计图可知,张明第2次的成绩为13.4秒,
故答案为:13.4;
(2)张明成绩的平均数为:=13.3(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(3)选择张明参加比赛,因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
【点睛】本题考查了平均数,中位数,方差的意义.平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
一、单选题
1.(2022春·内蒙古鄂尔多斯·八年级统考期末)某校“啦啦操”兴趣小组共有50名学生,她们的年龄分布如下表:
年龄/岁 12 13 14 15
人数 5 23 ■ ■
由于表格污损,14岁、15岁人数看不清,则下列关于年龄的统计量可以确定的是( ).
A.平均数、众数 B.众数、中位数 C.平均数、中位数 D.中位数、方差
2.(2022春·内蒙古呼伦贝尔·八年级统考期末)某校七年级1班50名同学在“森林草原防灭火”知识竞赛中的成绩如表所示:
成绩 60 70 80 90 100
人数 3 9 13 16 9
则这个班学生成绩的众数、中位数分别是( )
A.90,80 B.16,85 C.16,24.5 D.90,85
3.(2022春·内蒙古通辽·八年级校考期末)如果你和其余6人进入了八年级速算比赛的总决赛,你想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的( )
A.平均数 B.众数 C.中位数 D.方差
4.(2022春·内蒙古呼伦贝尔·八年级校考期末)在暑假到来之前,某机构向八年级学生推荐了A,B,C三条游学线路,现对全级学生喜欢哪一条游学线路作调查,以决定最终的游学线路,下面的统计量中最值得关注的是( )
A.方差 B.平均数 C.中位数 D.众数
5.(2022春·内蒙古呼伦贝尔·八年级校考期末)某商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如表所示
型号 22 22.5 23 23.5 24 24.5 25
数量(双) 2 6 11 15 7 3 4
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A.平均数 B.方差 C.中位数 D.众数
6.(2022春·内蒙古巴彦淖尔·八年级统考期末)一组数据的方差可以用式子表示,则式子中的数字50所表示的意义是( )
A.这组数据的个数 B.这组数据的平均数
C.这组数据的众数 D.这组数据的中位数
7.(2022春·内蒙古呼伦贝尔·八年级校考期末)已知一组数据的方差计算公式为:,由公式提供的信息,则下列说法错误的是( )
A.中位数是3 B.众数是3 C.平均数是3.5 D.方差是0.5
8.(2022春·内蒙古锡林郭勒盟·八年级校考期末)小明同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数 B.方差 C.中位数 D.众数
9.(2022春·内蒙古乌兰察布·八年级统考期末)某校举行课间操比赛,甲、乙两个班各选出20名学生参加比赛,两个班参赛学生的平均身高都为1.65m,其方差分别是S甲2=3.8,S乙2=3.4,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
二、填空题
10.(2022春·内蒙古呼伦贝尔·八年级校考期末)某学校要招聘一名教师,分笔试和面试两次考试,笔试、面试和最后得分的满分均为100分,竞聘教师的最后得分按笔试成绩:面试成绩=7∶3的比例计算.在这次招聘考试中,某竞聘教师的笔试成绩为90分,面试成绩为80分,则该竞聘教师的最后成绩是___________分.
11.(2022春·内蒙古呼伦贝尔·八年级校考期末)已知一组数据x1,x2,x3,x4,x5的平均数是2,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是_____.
12.(2022春·内蒙古巴彦淖尔·八年级统考期末)若一组数据2,3,x,5,7的众数为7,则这组数据的中位数为_________.
13.(2022春·内蒙古乌兰察布·八年级统考期末)已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是______.
14.(2022春·内蒙古呼伦贝尔·八年级统考期末)甲、乙两人5次射击命中的环数如下:
甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数==8,方差_____.(填“>”、“<”或“=”)
15.(2022春·内蒙古呼伦贝尔·八年级校考期末)一组数据﹣1,0,1,2,3的方差是_____.
16.(2022春·内蒙古呼伦贝尔·八年级统考期末)一组数据按从小到大的顺序排列为1,2,3,,4,5,若这组数据的中位数为3,则这组数据的方差是__________.
17.(2022春·内蒙古锡林郭勒盟·八年级校考期末)若一组数据x1,x2,…,xn的平均数是a,方差是b,则4x1﹣3,4x2﹣3,…,4xn﹣3的平均数是__________,方差是___________.
18.(2022春·内蒙古鄂尔多斯·八年级统考期末)下面是甲、乙两人10次射击成绩(环数)的条形统计图,则这两人10次射击命中环数的方差____.(填“>”、“<”或“=”)
19.(2022春·内蒙古呼和浩特·八年级统考期末)若甲、乙、丙、丁四位同学一学期4次数学测试的平均成绩恰好都是85分,方差分别为,,,,则成绩最稳定的同学是______.
三、解答题
20.(2022春·内蒙古乌兰察布·八年级统考期末)中考体育测试前,金川区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)扇形统计图中a= %,并补全条形统计图.
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、 个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
21.(2022春·内蒙古呼和浩特·八年级统考期末)中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生进行测试,并将测试得到的成绩汇成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中________%,并补全条形图;
(2)写出这次抽测中,测试成绩的众数和中位数,并解释它们的意义.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的人数.
22.(2022春·内蒙古呼伦贝尔·八年级校考期末)为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
初二1班体育模拟测试成绩分析表
平均分 方差 中位数 众数
男生 ________ 2 8 7
女生 7.92 1.99 8 ________
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由.
23.(2022春·内蒙古呼伦贝尔·八年级校考期末)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 7.5 5.4
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由
24.(2022春·内蒙古呼伦贝尔·八年级校考期末)6月26日是“国际禁毒日”,某中学组织七,八年级全体学生开展了“禁毒知识”网上竞赛活动,为了了解竞赛情况,从这两个年级分别随机抽取了10名学生的成绩,将收集到的数据整理分析并绘制成两个不完整的统计表.
整理数据:
人数分数 80 85 90 95 100
七年 2 2 3 2 1
八年 1 2 4 a 1
分析数据:
平均数 中位数 众数 方差
七年级 89 b 90 39
八年级 c 90 d 30
(1)______;______;______;______;
(2)该校七、八年级学生共有600人,本次竞赛成绩不低于90分为“优秀”估计这两个年级达到成绩“优秀”的学生共有多少人?
25.(2022春·内蒙古鄂尔多斯·八年级统考期末)某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)___________,___________;
(2)从方差的角度看,___________种西瓜的得分较稳定(填“甲”或“乙”);
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
26.(2022春·内蒙古呼伦贝尔·八年级校考期末)学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明第2次的成绩为: 秒;
(2)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
参考答案:
1.B
【分析】根据众数、中位数的定义进行判断即可.
【详解】解:由题意可知,“啦啦操”兴趣小组共有50人,中位数是从小到大排列后处在第25、26位学生年龄的平均数,而12岁的学生有5人,13岁的学生有23人,因此从小到大排列后,处在第25、26位的两个学生都是13岁,因此中位数是13岁,不受14岁、15岁人数的影响;因为13岁的学生有23人,而12岁的学生有5人,14岁、15岁的学生共有22人,因此众数是13岁.
故选:B.
【点睛】本题主要考查了中位数和众数的知识,正确掌握众数和中位数的定义是解题的关键.
2.D
【分析】根据众数的定义,找到该组数据中出现次数最多的数即为众数;根据中位数定义,将该组数据按从小到大依次排列,处于中间位置的两个数的平均数即为中位数.
【详解】解:90分的有16人,人数最多,故众数为90分;
处于中间位置的数为第25、26两个数,为80和90,
∴中位数为=85分.
故选:D.
【点睛】本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
3.C
【分析】根据题意可得:由中位数的概念,可知7人成绩的中位数是第4名的成绩.参赛选手要想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】解:由于总共有7个人,第4位选手的成绩是中位数,要判断是否进入前3名,
故应知道自己的成绩和中位数.
故选:C.
【点睛】本题考查的是中位数的含义,以及利用中位数作判断,理解中位数的含义是解本题的关键.
4.D
【详解】由于众数是数据中出现次数最多的数,
故全级学生喜欢的游学线路最值得关注的应该是统计调查数据的众数,
故选D.
5.D
【分析】根据众数的定义:一组数据中出现次数最多的数值,即可得解.
【详解】根据题意,销量最大,即为众数,故答案为D.
【点睛】此题主要考查对众数的理解运用,熟练掌握,即可解题.
6.B
【分析】根据方差公式的特点进行解答即可.
【详解】解:方差的定义:一般地设n个数据,x1,x2,…x的平均数为,则方差S2[(x1)2+(x2)2+…+(x)2],
所以50是这组数据的平均数.
故答案选:B
【点睛】此题考查了方差,熟练掌握方差的计算公式是解题的关键,一般地设n个数据,x1,x2,…x的平均数为,则方差S2[(x1)2+(x2)2+…+(x)2].
7.C
【分析】根据已知的方差计算公式得出这组数据为2、3、3、4,再根据中位数,众数,平均数以及方差的概念求解即可.
【详解】由题意可知这组数据为2、3、3、4、所以中位数为,故选项A不符题意.
众数为3,故选B不符合题意.
平均数为,故选项C符合题意.
方差为,故选项D不符题意,
故选C.
【点睛】本题主要考查方差,样本容量,中位数,众数及平均数的定义,掌握方差的计算公式是解题的关键.
8.C
【分析】利用平均数、中位数、方差和标准差的定义对各选项进行判断.
【详解】解:这组数据的平均数、方差和标准差都与第5个数有关,而这组数据的中位数为36与46的平均数,与第5个数无关.
故选:C.
【点睛】本题考查了方差:它也描述了数据对平均数的离散程度.也考查了中位数、平均数和众数的概念,解题的关键是熟练掌握平均数、中位数、方差和标准差的定义.
9.B
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定
【详解】S甲2=3.8,S乙2=3.4,
∴S甲2>S乙2,
∴参赛学生身高比较整齐的班级是乙班,
故选B.
【点睛】此题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
10.87
【分析】根据加权平均数的求法,求出该竞聘教师的最后成绩是多少即可.
【详解】解:∵(90×7+80×3)÷(7+3)
=870÷10
=87(分)
∴该竞聘教师的最后成绩是87分.
故答案为:87.
【点睛】此题主要考查了加权平均数的含义和求法,要熟练掌握,解答此题的关键是要明确:数据的权能够反映数据的相对“重要程度”,要突出某个数据,只需要给它较大的“权”,权的差异对结果会产生直接的影响.
11.4
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.先求数据x1,x2,x3,x4,x5的和,然后再用平均数的定义求新数据的平均数.
【详解】一组数据x1,x2,x3,x4,x5的平均数是2,有(x1+x2+x3+x4+x5)=2,
那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数是(3x1-2+3x2-2+3x3-2+3x4-2+3x5-2)=4.
故答案是:4.
【点睛】考查的是样本平均数的求法及运用,解题关键是记熟公式:.
12.5
【分析】根据众数的定义可得x的值,再依据中位数的定义即可得答案.
【详解】解:∵数据2,3,x,5,7的众数为7,
∴,
把这组数据从小到大排列为:2、3、5、7、7,
则中位数为5.
故答案为:5.
【点睛】本题考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.众数是数据中出现最多的一个数.
13.2.5
【分析】先根据众数是一组数据中出现次数最多的数据,求得x,再由中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
【详解】解:∵3与2都重复出现两次,众数是2,
∴x=2,
从小到大排列此数据为:1,2,2,2,3,3,5,7.
处在第4、5位的数分别是2,3,(2+3)÷2=2.5.
故答案为:2.5.
【点睛】本题主要考查了中位数和众数的定义,解题的关键在于能够熟练掌握中位数和众数的定义.
14.>
【分析】根据甲乙的数据利用方差的计算公式即可求解.
【详解】解:S2甲=[(7-8)2+(9 8)2+(8 8)2+(6 8)2+(10 8)2)]=2,
S2乙=[(7-8)2+(8 8)2+(9 8)2+(8 8)2+(8 8)2)]=0.4,
∴S2甲>S2乙.
故答案为:>.
【点睛】本题考查了方差的应用,解题的关键是熟练掌握方差的计算公式即可解决问题.
15.2
【详解】这组数据的平均数为:(-1+1+0+2+3)÷5=1,所以方差=[(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2.
16.
【详解】试题分析:根据中位数的求法可知=3,解得x=3,因此这组数的平均数为=,所以方差为s==.
考点:数据的分析
17. 4a﹣3 16b.
【详解】∵x1、x2…xn的平均数是a,
∴(x1、x2…xn)÷n=a
∴(4x1-3,4x2-3…4xn-3)÷4=4×a-3=4a-3,
∵x1、x2…xn的方差是b,
∴4x1-3,4x2-3…4xn-3的方差是4×4×b=16b.
答案是:4a-3;16b.
【点睛】本题考查平均数和方差的变换特点,若在原来数据前乘以同一个数,平均数也乘以同一个数,而方差要乘以这个数的平方,在数据上同加或减同一个数,方差不变.
18.>
【分析】先分别求出各自的平均数,再根据方差公式求出方差,即可作出比较.
【详解】甲的平均数
则
乙的平均数
则
所以
【点睛】本题属于基础应用题,只需学生熟练掌握方差的求法,即可完成.
19.丁
【分析】根据方差越大越不稳定,方差越小越稳定解答即可.
【详解】∵1.72>1.31>0.80>0.42,
∴丁同学的成绩最稳定.
故答案为丁.
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
20.(1)25,图见解析
(2)5,5
(3)810名
【分析】(1)用1减去其他天数所占的百分比即可得到a的值,用360°乘以它所占的百分比,即可求出该扇形所对圆心角的度数;
(2)根据众数与中位数的定义求解即可;
(3)先求出样本中得满分的学生所占的百分比,再乘以1800即可.
【详解】(1)解:扇形统计图中a=1-30%-15%-10%-20%=25%,
设引体向上6个的学生有x人,由题意得
,解得x=50.
条形统计图补充如下:
故答案为:5;
(2)解:由条形图可知,引体向上5个的学生有60人,人数最多,所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,故中位数为(5+5)÷2=5.
故答案为:5,5.
(3)解:(名).
答:估计该区体育中考选报引体向上的男生能获得满分的同学有810名.
【点睛】本题考查了众数与中位数的意义.一组数据中出现次数最多的数据叫做众数;将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.也考查了条形统计图、扇形统计图与用样本估计总体.
21.(1)25,见解析
(2)众数是5,中位数是5;众数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多;中位数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多
(3)810名
【分析】(1)根据扇形统计图可以求得a的值,根据扇形统计图和条形统计图可以得到做6个的学生数,从而可以将条形图;
(2)根据众数与中位数的定义求解即可;
(3)先求出样本中得满分的学生所占的百分比,再乘以1800即可.
(1)
解:扇形统计图中,
设引体向上6个的学生有x人,
由题意得
解得.
条形统计图补充如下:
答案为:25;
(2)
解:由条形图可知,引体向上5个的学生有60人,人数最多,所以众数是5;
共200名同学,排序后第100名与第101名同学的成绩都是5个,故中位数为
众数表示的意义:这次的抽样调查中,说明初三男生引体向上的成绩集中在5个的人数最多;
中位数表示的意义:这次的抽样调查中,说明一半初三男生引体向上的成绩大于等于5个,另一半初三男生引体向上的成绩小于等于5个;
(3)
解:(名).
答:估计该区体育中考选报引体向上的男生能获得满分的同学有810名.
【点睛】本题为统计题,考查众数与中位数的意义.一组数据中出现次数最多的数据叫做众数;将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数.也考查了条形统计图、扇形统计图与用样本估计总体.
22.(1)20、25;(2)见解析;(3)见解析
【分析】(1)由条形图可得男生总人数,总人数减去男生人数可得女生人数;
(2)根据平均数和众数定义可得;
(3)可根据众数比较得出答案.
【详解】解:(1)这个班共有男生人,共有女生人,
故答案为:20、25;
(2)甲的平均分为,女生的众数为8,
补全表格如下:
平均分 方差 中位数 众数
男生 7.9 2 8 7
女生 7.92 1.99 8 8
(3)从众数看,女生队的众数高于男生队的众数,所以女生队表现更突出.
【点睛】本题主要考查平均数、众数及条形图、扇形图,根据统计图得出解题所需数据,并熟练掌握平均数和众数的定义是解题的关键.
23.(1)见解析
(2)甲胜出,方差小,见解析
【分析】(1)分别利用中位数以及方差和平均数求法得出即可;
(2)根据(1)计算出的甲乙两人的方差,比较大小即可做出判断.
(1)
根据折线统计图得:
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:×(2+4+6+8+7+7+8+9+9+10)=7(环),
甲的射击成绩为9,6,7,6,5,7,7,?,8,9,平均数为7环,
则甲第八环成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),
所以甲的10次成绩为:9,6,7,6,5,7,7,6,8,9,
把这些数从小到大排列为5,6,6,6,7,7,7,8,9,9,
则中位数是:=7(环),
甲的方差为:;
乙命中10环的次数为1.
补统计表如下:
平均数 中位数 方差 命中10环的次数
甲 7 7 1.6 0
乙 7 7.5 5.4 1
补全折线统计图如下:
(2)
由甲的方差小于乙的方差,甲比较稳定,故甲胜出.
【点睛】此题考查了折线统计图,中位数,方差,平均数,以及统计表,掌握相关统计量的计算方法是解本题的关键.
24.(1);;;
(2)估计这两个年级达到成绩“优秀”的学生共有390人
【分析】(1)根据提供数据确定八年级95分的人数,利用众数中位数及平均数分别确定其他未知数即可.
(2)用样本的平均数估计总体的平均数即可.
【详解】(1)八年级95分的有10-1-2-4-1=2(人),故a=2,
七年级的中位数为,故b=90,
八年级的平均数为,故,
八年级中90分的最多,故,
故答案为:2,90,90,90;
(2)(人),
答:估计这两个年级达到成绩优秀的学生共有390人.
【点睛】本题考查了中位数,众数,平均数等统计基础知识,明确相关统计量表示的意义及相关计算是解题的关键.
25.(1)a=88,b=90;(2)乙;(3)见解析
【分析】(1)根据中位数、众数的意义求解即可;
(2)根据数据大小波动情况,直观可得答案;
(3)从方差、中位数、众数的比较得出答案.
【详解】解:(1)甲品种西瓜测评得分从小到大排列处在中间位置的一个数是88,所以中位数是88,即a=88,
将乙品种西瓜的测评得分出现次数最多的是90分,因此众数是90,即b=90,
故答案为:a=88,b=90;
(2)由甲、乙两种西瓜的测评得分的大小波动情况,直观可得S乙2<S甲2,
故答案为:乙;
(3)小明认为甲种西瓜的品质较好些,是因为甲的得分众数比乙的得分众数高;小军认为乙种西瓜的品质较好些,是因为乙的得分方差小和得分中位数比甲的高.
【点睛】本题考查统计表,中位数、众数、平均数,理解中位数、众数、平均数的意义和计算方法是正确解答的前提.
26.(1)13.4;
(2)13.3,13.3,0.02;
(3)选择张明参加比赛,理由见解析.
【分析】(1)根据统计图给出的数据可直接得出答案;
(2)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(3)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:根据统计图可知,张明第2次的成绩为13.4秒,
故答案为:13.4;
(2)张明成绩的平均数为:=13.3(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(3)选择张明参加比赛,因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
【点睛】本题考查了平均数,中位数,方差的意义.平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
