北师大版七年级下册 4.4用尺规作三角形基础练习 含答案
文档属性
| 名称 | 北师大版七年级下册 4.4用尺规作三角形基础练习 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 11:20:31 | ||
图片预览



文档简介
4.4用尺规作三角形 基础练习
一、单选题
1.已知线段,,,求作:,使,,.下面的作图顺序正确的是( )
①以点为圆心,以为半径画弧,以点为圆心,以为半径画弧,两弧交于点;
②作线段等于;
③连接,,则就是所求作图形.
A.①②③ B.③②① C.②①③ D.②③①
2.尺规作图是指( )
A.用直尺规范作图 B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图 D.直尺和圆规是作图工具
3.根据下列条件能画出唯一确定的的是( )
A. B.
C. D.
4.尺规作图的画图工具是( )
A.刻度尺、圆规 B.三角板和量角器
C.直尺和量角器 D.没有刻度的直尺和圆规
5.利用尺规作图,不能作出唯一的三角形的是( )
A.已知两边及夹角 B.已知两角及夹边
C.已知两边及一边的对角 D.已知三边
6.下列条件能作出唯一的三角形的是( )
A.AB=3cm,∠B=30° B.∠A=30°,∠B=60°
C.AB=2cm,BC=3cm,AC=5cm D.AB=4cm,BC=3cm,AC=5cm
7.根据以下条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角 利用尺规作图能用尺规作出唯一的三角形有( )
A.①② B.①③ C.①②③ D.①②④
8.用直尺和圆规作两个全等三角形,如图,能得到△COD≌△C'O'D'的依据是( )
A.SAA B.SSS C.ASA D.AAS
9.在△ABC中,AB=AC,∠A=80°,进行如下操作:
①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E、F;
②分别以E、F为圆心,以大于EF长为半径作弧,两弧交于点M;
③作射线BM交AC于点D,
则∠BDC的度数为( ).
A.100° B.65° C.75° D.105°
10.下列各条件不能作出唯一直角三角形的是( )
A.已知两直角边 B.已知两锐角
C.已知一直角边和它们所对的锐角 D.已知斜边和一直角边
二、填空题
11.在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角已知:∠AOB, 求作:∠A′OB′,使:∠A′OB′=∠AOB
小易同学作法如下:
①作射线O′A′;②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D; ③以点O′为圆心,以OC长为半径作弧,交O′A于C ④以点C′圆心,以CD为半径作弧,交③中所画弧于D′; ⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.
老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
12.如图,以A、B两点为其中两个顶点作位置不同的等边三角形,最多可以作出_____个.
13.已知线段a,b,c,求作,使.
①以点B为圆心,c的长为半径画弧;
②连接;
③作;
④以点C为圆心,b的长为半径画弧,两弧交于点A.
作法的合理顺序是__________.
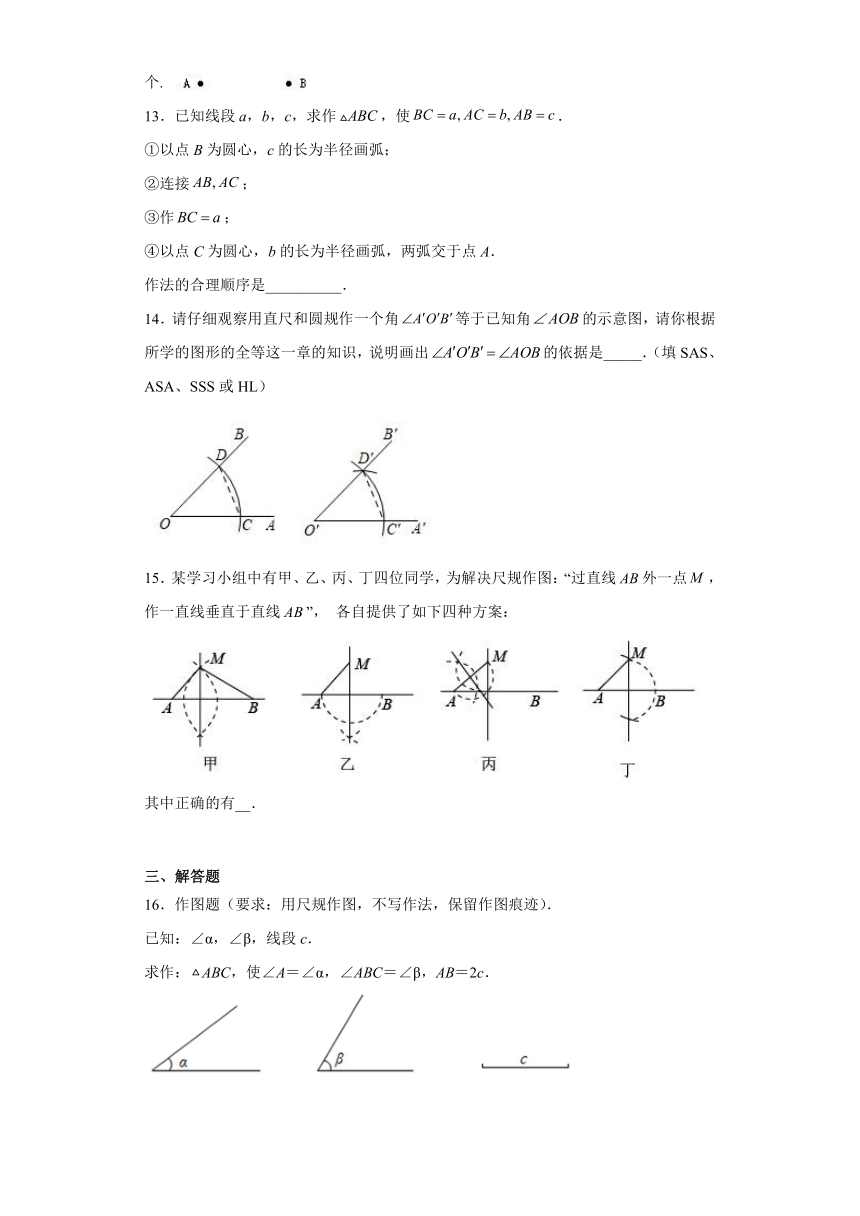
14.请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的图形的全等这一章的知识,说明画出的依据是_____.(填SAS、ASA、SSS或HL)
15.某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线外一点,作一直线垂直于直线”, 各自提供了如下四种方案:
其中正确的有__.
三、解答题
16.作图题(要求:用尺规作图,不写作法,保留作图痕迹).
已知:∠α,∠β,线段c.
求作:ABC,使∠A=∠α,∠ABC=∠β,AB=2c.
17.已知:直线l和l外一点P.
求作:直线l的垂线,使它经过点P.
作法:
①在直线l上任取两点A、B;
②分别以点A、B为圆心,AP,BP长为半径作弧,在直线l下方两弧交于点C;
③作直线PC.
所以直线PC为所求作的垂线.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AP、AC、BP、BC.
∵AP=AC,BP=BC,AB=AB,
∴△APB≌△ACB( )(填推理依据).
∴∠PAB=∠CAB,
∴PC⊥AB( )(填推理依据).
18.如图, 已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两个内角的夹边等于a.
19.如图,已知△ABC中,AB=2,BC=4
(1)画出△ABC的高AD和CE;
(2)若AD=,求CE的长.
20.如图,小明不慎将一块三角形模具打碎为三块,请利用学过的知识画出一个与原来三角形模具一样的三角形.
参考答案
1.C
2.C
3.C
4.D
5.C
6.D
7.C
8.B
9.D
10.B
11.SSS(三角形全等或全等三角形的对应角相等)
12.2
13.③①④②
14.
15.甲、乙、丙
16.解:△ABC即为所求作的三角形.
17.解:(1)
(2)SSS,等腰三角形三线合一
18.解:如图,
如图,△ABC即为所求.
19.解:(1)过点A作AD⊥CB,交CB延长线于点D,过点C作CE⊥AB,交AB延长线于点E,则AD、CE即为所求,如图所示:
(2)∵S△ABC=×AD×BC=AB×CE,
∴××4=×2×CE,
∴CE=3.
20.解:如图所示:△ABC与原来三角形模具一样.
.
一、单选题
1.已知线段,,,求作:,使,,.下面的作图顺序正确的是( )
①以点为圆心,以为半径画弧,以点为圆心,以为半径画弧,两弧交于点;
②作线段等于;
③连接,,则就是所求作图形.
A.①②③ B.③②① C.②①③ D.②③①
2.尺规作图是指( )
A.用直尺规范作图 B.用刻度尺和圆规作图
C.用没有刻度的直尺和圆规作图 D.直尺和圆规是作图工具
3.根据下列条件能画出唯一确定的的是( )
A. B.
C. D.
4.尺规作图的画图工具是( )
A.刻度尺、圆规 B.三角板和量角器
C.直尺和量角器 D.没有刻度的直尺和圆规
5.利用尺规作图,不能作出唯一的三角形的是( )
A.已知两边及夹角 B.已知两角及夹边
C.已知两边及一边的对角 D.已知三边
6.下列条件能作出唯一的三角形的是( )
A.AB=3cm,∠B=30° B.∠A=30°,∠B=60°
C.AB=2cm,BC=3cm,AC=5cm D.AB=4cm,BC=3cm,AC=5cm
7.根据以下条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角 利用尺规作图能用尺规作出唯一的三角形有( )
A.①② B.①③ C.①②③ D.①②④
8.用直尺和圆规作两个全等三角形,如图,能得到△COD≌△C'O'D'的依据是( )
A.SAA B.SSS C.ASA D.AAS
9.在△ABC中,AB=AC,∠A=80°,进行如下操作:
①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E、F;
②分别以E、F为圆心,以大于EF长为半径作弧,两弧交于点M;
③作射线BM交AC于点D,
则∠BDC的度数为( ).
A.100° B.65° C.75° D.105°
10.下列各条件不能作出唯一直角三角形的是( )
A.已知两直角边 B.已知两锐角
C.已知一直角边和它们所对的锐角 D.已知斜边和一直角边
二、填空题
11.在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角已知:∠AOB, 求作:∠A′OB′,使:∠A′OB′=∠AOB
小易同学作法如下:
①作射线O′A′;②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D; ③以点O′为圆心,以OC长为半径作弧,交O′A于C ④以点C′圆心,以CD为半径作弧,交③中所画弧于D′; ⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.
老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
12.如图,以A、B两点为其中两个顶点作位置不同的等边三角形,最多可以作出_____个.
13.已知线段a,b,c,求作,使.
①以点B为圆心,c的长为半径画弧;
②连接;
③作;
④以点C为圆心,b的长为半径画弧,两弧交于点A.
作法的合理顺序是__________.
14.请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的图形的全等这一章的知识,说明画出的依据是_____.(填SAS、ASA、SSS或HL)
15.某学习小组中有甲、乙、丙、丁四位同学,为解决尺规作图:“过直线外一点,作一直线垂直于直线”, 各自提供了如下四种方案:
其中正确的有__.
三、解答题
16.作图题(要求:用尺规作图,不写作法,保留作图痕迹).
已知:∠α,∠β,线段c.
求作:ABC,使∠A=∠α,∠ABC=∠β,AB=2c.
17.已知:直线l和l外一点P.
求作:直线l的垂线,使它经过点P.
作法:
①在直线l上任取两点A、B;
②分别以点A、B为圆心,AP,BP长为半径作弧,在直线l下方两弧交于点C;
③作直线PC.
所以直线PC为所求作的垂线.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AP、AC、BP、BC.
∵AP=AC,BP=BC,AB=AB,
∴△APB≌△ACB( )(填推理依据).
∴∠PAB=∠CAB,
∴PC⊥AB( )(填推理依据).
18.如图, 已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两个内角的夹边等于a.
19.如图,已知△ABC中,AB=2,BC=4
(1)画出△ABC的高AD和CE;
(2)若AD=,求CE的长.
20.如图,小明不慎将一块三角形模具打碎为三块,请利用学过的知识画出一个与原来三角形模具一样的三角形.
参考答案
1.C
2.C
3.C
4.D
5.C
6.D
7.C
8.B
9.D
10.B
11.SSS(三角形全等或全等三角形的对应角相等)
12.2
13.③①④②
14.
15.甲、乙、丙
16.解:△ABC即为所求作的三角形.
17.解:(1)
(2)SSS,等腰三角形三线合一
18.解:如图,
如图,△ABC即为所求.
19.解:(1)过点A作AD⊥CB,交CB延长线于点D,过点C作CE⊥AB,交AB延长线于点E,则AD、CE即为所求,如图所示:
(2)∵S△ABC=×AD×BC=AB×CE,
∴××4=×2×CE,
∴CE=3.
20.解:如图所示:△ABC与原来三角形模具一样.
.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
