2023年中考数学复习:一次函数(含答案)
文档属性
| 名称 | 2023年中考数学复习:一次函数(含答案) | 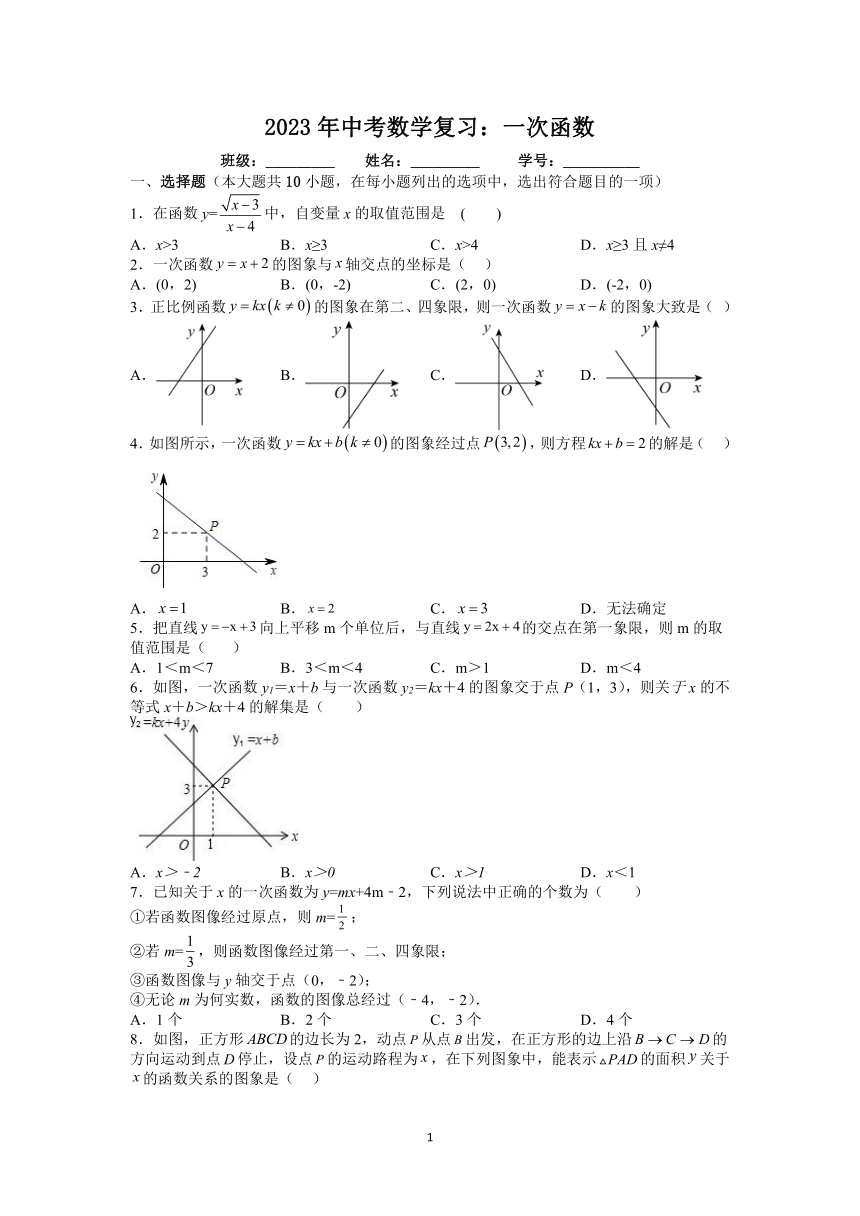 | |
| 格式 | zip | ||
| 文件大小 | 447.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 11:58:49 | ||
图片预览





文档简介
2023年中考数学复习:一次函数
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.在函数y=中,自变量x的取值范围是 ( )
A.x>3 B.x≥3 C.x>4 D.x≥3且x≠4
2.一次函数的图象与轴交点的坐标是( )
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
3.正比例函数的图象在第二、四象限,则一次函数的图象大致是( )
A. B. C. D.
4.如图所示,一次函数的图象经过点,则方程的解是( )
A. B. C. D.无法确定
5.把直线向上平移m个单位后,与直线的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
6.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>﹣2 B.x>0 C.x>1 D.x<1
7.已知关于x的一次函数为y=mx+4m﹣2,下列说法中正确的个数为( )
①若函数图像经过原点,则m=;
②若m=,则函数图像经过第一、二、四象限;
③函数图像与y轴交于点(0,﹣2);
④无论m为何实数,函数的图像总经过(﹣4,﹣2).
A.1个 B.2个 C.3个 D.4个
8.如图,正方形的边长为2,动点从点出发,在正方形的边上沿的方向运动到点停止,设点的运动路程为,在下列图象中,能表示的面积关于的函数关系的图象是( )
A. B. C. D.
9.若直线经过点,经过点,且与关于轴对称,则与的交点坐标为( )
A. B. C. D.
10.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A.4 B.8 C.16 D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知函数是关于x的一次函数,则______.
12.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是_____.
13.如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为_______.
14.根据如图所示的程序计算函数值,若输入x的值1.5,则输出的y值为 __.
15.若方程组无解,则图象不经过第________象限.
16.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是___.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.已知一次函数.
(1)求证:点在该函数图象上;
(2)若该函数图象向上平移2个单位后过点,求k的值;
(3)若,点在函数图象上,且,请比较与的大小,并说明理由.
18.如图,在平面直角坐标系xOy中,直线:与y轴交于点Q,且与直线:相交于点P,其中点P纵坐标为1.
(1)求点P的坐标及的值;
(2)求△PQO的面积;
(3)直接写出不等式的解集.
19.习近平总书记对实施乡村振兴战略作出重要指示强调:实施乡村振兴战略,是党的十九大作出的重大决策部署,是新时代做好“三农”工作的总抓手.为了发展特色产业,红旗村花费4000元集中采购了种树苗500株,种树苗400株,已知种树苗单价是种树苗单价的1.25倍.
(1)求、两种树苗的单价分别是多少元?
(2)红旗村决定再购买同样的树苗100株用于补充栽种,其中种树苗不多于25株,在单价不变,总费用不超过480元的情况下,共有几种购买方案?哪种方案费用最低?最低费用是多少元?
20.A,B两地相距,甲、乙两人分别开车从A地出发前往B地,其中甲先出发,如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题:
(1)填空:甲的速度为___________;
(2)分别求出与x之间的函数解析式;
(3)求出点C的坐标,并写点C的实际意义.
21.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.
22.如图,在平面直角坐标系xOy中,已知直线AB:y=x+4交x轴于点A,交y轴于点B.直线CD:y=-x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,请直接写出点P坐标并求出所有符合条件的点E的坐标;若不存在,请说明理由.
答案:
1.D 2.D 3.A 4.C 5.C 6.C 7.B 8.D 9.B 10.C 11.-2
12.x=2 13.﹣4≤m≤4 14. 15.二 16.12
17.(1)令,得,
∴点在函数图象上;
(2)一次函数图象向上平移2个单位得,
将代入得:,
解得;
(3),理由如下:
∵,
∴y随x的增大而减小,
∵点在图象上,且,
∴.
18(1)解:把y=1代入y=-x得,-x=1,
解得x=-2,
∴点P的坐标为(-2,1),
把P点的坐标代入y=x+a得,1=-2+a,
解得a=3;
(2)解:∵直线l1:y=x+3与y轴交于点Q,
∴Q(0,3),
∴OQ=3,
∴S△POQ=×3×2=3;
(3)解:由图象可知,不等式 x≤x+a的解集是x≥-2.
19.(1)解:设种树苗的单价是x元,则B种树苗的单价是1.25x元,根据题意得:
,
解得:,
∴1.25x=5,
答:种树苗的单价是4元,则B种树苗的单价是5元;
(2)解:设购买种树苗a棵,则购买B种树苗(100-a)棵,其中a为正整数,根据题意得:
,
解得:,
∵a为正整数,
∴a取20,21,22,23,24,25,
∴有6种购买方案,
设总费用为w元,
∴,
∵-1<0,
∴w随a的增大而减小,
∴当a=25时,w最小,最小值为475,
此时100-a=75,
答:有6种购买方案,购买种树苗,25棵,购买B种树苗75棵费用最低,最低费用是475元.
20.(1)解:观察图象,由甲先出发可知甲从A地到B地用了,
∵A,B两地相距,
∴甲的速度为,
故答案为:60;
(2)解:设与x之间的函数解析式为,
将点,代入得,
解得,
∴与x之间的函数解析式为,
同理,设与x之间的函数解析式为,
将点,代入得,
解得,
∴与x之间的函数解析式为;
(3)解:将与x之间的函数解析式联立得,
,
解得,
∴点C的坐标为,
点C的实际意义为:甲出发时,乙追上甲,此时两人距A地.
21.解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E,
∴∠CAD+∠DCA=90°,
∵∠BAC=90°,
∴∠CAD+∠BAE=90°,
∴∠BAE=∠ACD,
在和中,
,
∴≌(AAS),
∴CD=AE,AD=BE,
∵A(2,0)、B(3,3),
∴OA=2,OE=BE=3,
∴CD=AE=1,OD=AD﹣OA=1,
∴C的坐标是(﹣1,1);
(2)如图,作BE⊥x轴于E,
设直线BC的解析式为y=kx+b,
∵B点的坐标为(3,3),C点的坐标是(﹣1,1),
∴,
解得,,
∴直线BC的解析式为y=x+,
当x=0时,y=,
∴OM=,
∴的面积=梯形MOEB的面积﹣的面积﹣的面积
=×(+3)×3﹣×2×﹣×1×3
=;
(3)如图,作M关于x轴的对称点(0,﹣),连接B,交x轴于点P,此时PB+PM=PB+P=B的值最小,
设直线B的解析式为y=mx+n,
则,
解得,,
∴直线B的解析式为y=x﹣,
点P在x轴上,当y=0时,x=1,
∴点P的坐标为(1,0).
22.解:(1)∵点B是直线AB:y=x+4与y轴的交点坐标,
∴B(0,4),
∵点D是直线CD:y=-x-1与y轴的交点坐标,
∴D(0,-1);
(2)如图1,
∵直线AB与CD相交于M,
∴
①-②可得:x+5=0,
∴x=-5,
把x=-5代入②可得:y=,
∴M坐标为(-5,),
∵B(0,4),D(0,-1),
∴BD=5,
∵点P在射线MD上,
当P在MD的延长线上时,x≥0,
S=S△BDM+S△BDP=×5(5+x)= ,
当P在线段MD上时,-5<x<0,
S=S△BDM-S△BDP=×5(5+x)=,
∴S=( x>-5)
(3)如图,
由(2)知,S=,
当S=20时,=20,
∴x=3,
∴P(3,-2),
①当BP是对角线时,取BP的中点G,连接MG并延长取一点E'使GE'=GM,
设E'(m,n),
∵B(0,4),P(3,-2),
∴BP的中点坐标为(,1),
∵M(-5, ),
∴,
∴m=8,n=,
∴E'(8,),
②当AB为对角线时,同①的方法得,E(-8,),
③当MP为对角线时,同①的方法得,E''(-2,-),
即:满足条件的点E的坐标为(8,)、(-8, )、(-2,-).
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.在函数y=中,自变量x的取值范围是 ( )
A.x>3 B.x≥3 C.x>4 D.x≥3且x≠4
2.一次函数的图象与轴交点的坐标是( )
A.(0,2) B.(0,-2) C.(2,0) D.(-2,0)
3.正比例函数的图象在第二、四象限,则一次函数的图象大致是( )
A. B. C. D.
4.如图所示,一次函数的图象经过点,则方程的解是( )
A. B. C. D.无法确定
5.把直线向上平移m个单位后,与直线的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
6.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>﹣2 B.x>0 C.x>1 D.x<1
7.已知关于x的一次函数为y=mx+4m﹣2,下列说法中正确的个数为( )
①若函数图像经过原点,则m=;
②若m=,则函数图像经过第一、二、四象限;
③函数图像与y轴交于点(0,﹣2);
④无论m为何实数,函数的图像总经过(﹣4,﹣2).
A.1个 B.2个 C.3个 D.4个
8.如图,正方形的边长为2,动点从点出发,在正方形的边上沿的方向运动到点停止,设点的运动路程为,在下列图象中,能表示的面积关于的函数关系的图象是( )
A. B. C. D.
9.若直线经过点,经过点,且与关于轴对称,则与的交点坐标为( )
A. B. C. D.
10.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A.4 B.8 C.16 D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.已知函数是关于x的一次函数,则______.
12.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是_____.
13.如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为_______.
14.根据如图所示的程序计算函数值,若输入x的值1.5,则输出的y值为 __.
15.若方程组无解,则图象不经过第________象限.
16.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是___.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.已知一次函数.
(1)求证:点在该函数图象上;
(2)若该函数图象向上平移2个单位后过点,求k的值;
(3)若,点在函数图象上,且,请比较与的大小,并说明理由.
18.如图,在平面直角坐标系xOy中,直线:与y轴交于点Q,且与直线:相交于点P,其中点P纵坐标为1.
(1)求点P的坐标及的值;
(2)求△PQO的面积;
(3)直接写出不等式的解集.
19.习近平总书记对实施乡村振兴战略作出重要指示强调:实施乡村振兴战略,是党的十九大作出的重大决策部署,是新时代做好“三农”工作的总抓手.为了发展特色产业,红旗村花费4000元集中采购了种树苗500株,种树苗400株,已知种树苗单价是种树苗单价的1.25倍.
(1)求、两种树苗的单价分别是多少元?
(2)红旗村决定再购买同样的树苗100株用于补充栽种,其中种树苗不多于25株,在单价不变,总费用不超过480元的情况下,共有几种购买方案?哪种方案费用最低?最低费用是多少元?
20.A,B两地相距,甲、乙两人分别开车从A地出发前往B地,其中甲先出发,如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题:
(1)填空:甲的速度为___________;
(2)分别求出与x之间的函数解析式;
(3)求出点C的坐标,并写点C的实际意义.
21.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,
(1)求点C的坐标;
(2)连接AM,求△AMB的面积;
(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.
22.如图,在平面直角坐标系xOy中,已知直线AB:y=x+4交x轴于点A,交y轴于点B.直线CD:y=-x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,请直接写出点P坐标并求出所有符合条件的点E的坐标;若不存在,请说明理由.
答案:
1.D 2.D 3.A 4.C 5.C 6.C 7.B 8.D 9.B 10.C 11.-2
12.x=2 13.﹣4≤m≤4 14. 15.二 16.12
17.(1)令,得,
∴点在函数图象上;
(2)一次函数图象向上平移2个单位得,
将代入得:,
解得;
(3),理由如下:
∵,
∴y随x的增大而减小,
∵点在图象上,且,
∴.
18(1)解:把y=1代入y=-x得,-x=1,
解得x=-2,
∴点P的坐标为(-2,1),
把P点的坐标代入y=x+a得,1=-2+a,
解得a=3;
(2)解:∵直线l1:y=x+3与y轴交于点Q,
∴Q(0,3),
∴OQ=3,
∴S△POQ=×3×2=3;
(3)解:由图象可知,不等式 x≤x+a的解集是x≥-2.
19.(1)解:设种树苗的单价是x元,则B种树苗的单价是1.25x元,根据题意得:
,
解得:,
∴1.25x=5,
答:种树苗的单价是4元,则B种树苗的单价是5元;
(2)解:设购买种树苗a棵,则购买B种树苗(100-a)棵,其中a为正整数,根据题意得:
,
解得:,
∵a为正整数,
∴a取20,21,22,23,24,25,
∴有6种购买方案,
设总费用为w元,
∴,
∵-1<0,
∴w随a的增大而减小,
∴当a=25时,w最小,最小值为475,
此时100-a=75,
答:有6种购买方案,购买种树苗,25棵,购买B种树苗75棵费用最低,最低费用是475元.
20.(1)解:观察图象,由甲先出发可知甲从A地到B地用了,
∵A,B两地相距,
∴甲的速度为,
故答案为:60;
(2)解:设与x之间的函数解析式为,
将点,代入得,
解得,
∴与x之间的函数解析式为,
同理,设与x之间的函数解析式为,
将点,代入得,
解得,
∴与x之间的函数解析式为;
(3)解:将与x之间的函数解析式联立得,
,
解得,
∴点C的坐标为,
点C的实际意义为:甲出发时,乙追上甲,此时两人距A地.
21.解:(1)如图,作CD⊥x轴于D,BE⊥x轴于E,
∴∠CAD+∠DCA=90°,
∵∠BAC=90°,
∴∠CAD+∠BAE=90°,
∴∠BAE=∠ACD,
在和中,
,
∴≌(AAS),
∴CD=AE,AD=BE,
∵A(2,0)、B(3,3),
∴OA=2,OE=BE=3,
∴CD=AE=1,OD=AD﹣OA=1,
∴C的坐标是(﹣1,1);
(2)如图,作BE⊥x轴于E,
设直线BC的解析式为y=kx+b,
∵B点的坐标为(3,3),C点的坐标是(﹣1,1),
∴,
解得,,
∴直线BC的解析式为y=x+,
当x=0时,y=,
∴OM=,
∴的面积=梯形MOEB的面积﹣的面积﹣的面积
=×(+3)×3﹣×2×﹣×1×3
=;
(3)如图,作M关于x轴的对称点(0,﹣),连接B,交x轴于点P,此时PB+PM=PB+P=B的值最小,
设直线B的解析式为y=mx+n,
则,
解得,,
∴直线B的解析式为y=x﹣,
点P在x轴上,当y=0时,x=1,
∴点P的坐标为(1,0).
22.解:(1)∵点B是直线AB:y=x+4与y轴的交点坐标,
∴B(0,4),
∵点D是直线CD:y=-x-1与y轴的交点坐标,
∴D(0,-1);
(2)如图1,
∵直线AB与CD相交于M,
∴
①-②可得:x+5=0,
∴x=-5,
把x=-5代入②可得:y=,
∴M坐标为(-5,),
∵B(0,4),D(0,-1),
∴BD=5,
∵点P在射线MD上,
当P在MD的延长线上时,x≥0,
S=S△BDM+S△BDP=×5(5+x)= ,
当P在线段MD上时,-5<x<0,
S=S△BDM-S△BDP=×5(5+x)=,
∴S=( x>-5)
(3)如图,
由(2)知,S=,
当S=20时,=20,
∴x=3,
∴P(3,-2),
①当BP是对角线时,取BP的中点G,连接MG并延长取一点E'使GE'=GM,
设E'(m,n),
∵B(0,4),P(3,-2),
∴BP的中点坐标为(,1),
∵M(-5, ),
∴,
∴m=8,n=,
∴E'(8,),
②当AB为对角线时,同①的方法得,E(-8,),
③当MP为对角线时,同①的方法得,E''(-2,-),
即:满足条件的点E的坐标为(8,)、(-8, )、(-2,-).
同课章节目录
