四川省成都市名校2022-2023学年高二下学期期中考试数学(文)试题(PDF版含答案)
文档属性
| 名称 | 四川省成都市名校2022-2023学年高二下学期期中考试数学(文)试题(PDF版含答案) | 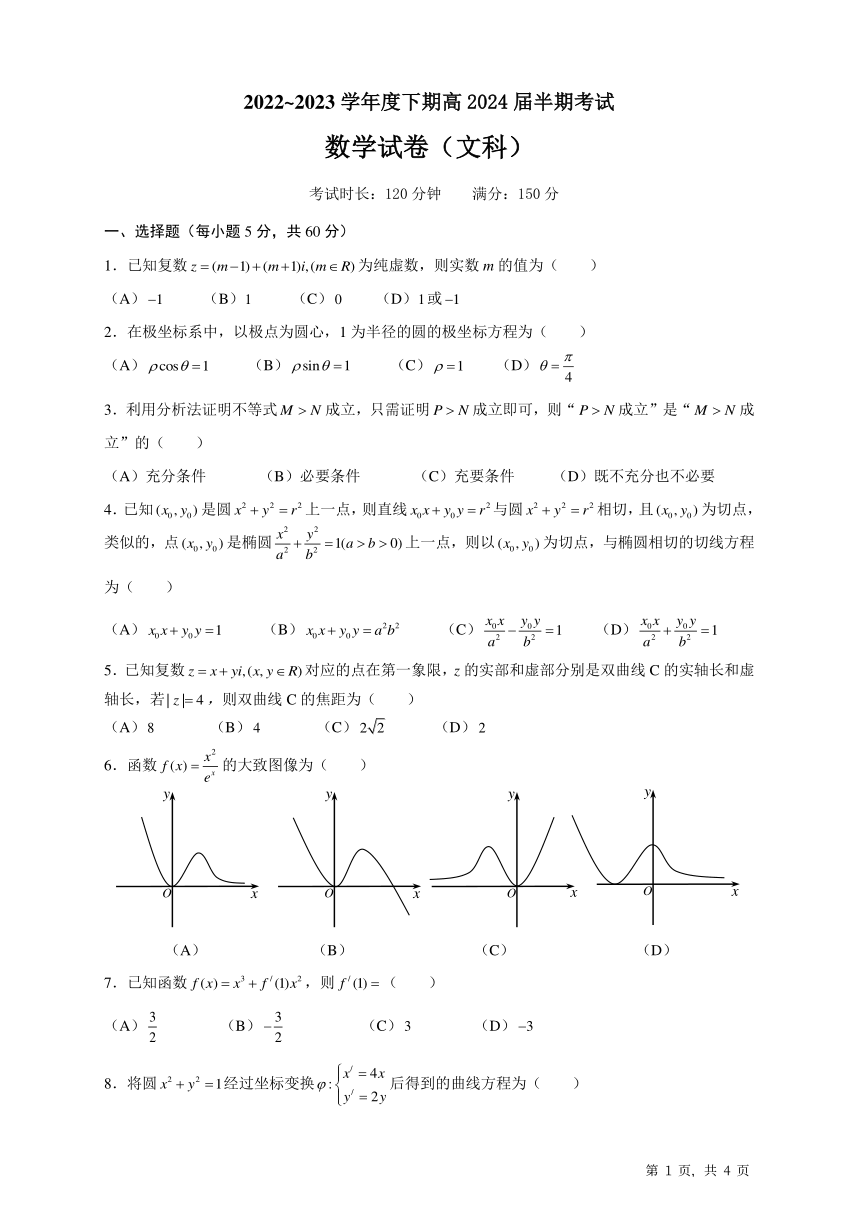 | |
| 格式 | |||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 22:00:40 | ||
图片预览




文档简介
2022~2023 学年度下期高 2024 届半期考试
数学试卷(文科)
考试时长:120分钟 满分:150分
一、选择题(每小题 5 分,共 60 分)
1.已知复数 z (m 1) (m 1)i, (m R)为纯虚数,则实数 m 的值为( )
(A) 1 (B)1 (C) 0 (D)1或 1
2.在极坐标系中,以极点为圆心,1 为半径的圆的极坐标方程为( )
(A) cos 1 (B) sin 1 (C) 1 (D)
4
3.利用分析法证明不等式M N 成立,只需证明 P N 成立即可,则“ P N 成立”是“M N 成
立”的( )
(A)充分条件 (B)必要条件 (C)充要条件 (D)既不充分也不必要
4.已知 (x 是圆 20 , y0 ) x y
2 r2 上一点,则直线 x0x y
2 与圆 2 2
0 y r x y r
2 相切,且 (x , y ) 为切点,0 0
x2 y2
类似的,点 (x0 , y 是椭圆0 ) 1(a b 0)上一点,则以 (x0 , y ) 为切点,与椭圆相切的切线方程 2 2 0a b
为( )
x x y y x x y y
(A) x0x y y 1 (B)0 x0x y y a
2b2 (C) 0 0 1 (D) 0 00 1
a2 b2 a2 b2
5.已知复数 z x yi, (x, y R)对应的点在第一象限,z 的实部和虚部分别是双曲线 C 的实轴长和虚
轴长,若 | z | 4 ,则双曲线 C 的焦距为( )
(A)8 (B) 4 (C) 2 2 (D) 2
x2
6.函数 f (x) 的大致图像为( )
ex
y y y y
O x O x O x O x
(A) (B) (C) (D)
7.已知函数 f (x) x3 f / (1)x2 ,则 f / (1) ( )
3 3
(A) (B) (C)3 (D) 3
2 2
x / 4x
8.将圆 x2 y2 1经过坐标变换 : 后得到的曲线方程为( )
/
y 2y
第 1 页,共 4 页
第 2 页,共 4 页
三、解答题(共 70 分)
17.(本小题 10 分)已知曲线 C 的极坐标方程为 2 4 cos 3,A, B 是曲线 C 上不同的两点,且
OA 2OB,其中O 为极点.
(Ⅰ)求曲线 C 的直角坐标方程;
(Ⅱ)求点 B 的极径.
18.(本小题 12 分)某企业生产的某种乳制品的蛋白质含量 x(%)与生产成本 y(元)之间的数据
如下表:
x 0 0.69 1.39 1.79 2.40 2.56 2.94
y 19 32 40 44 52 53 54
已知生产成本 y 与产品蛋白质含量 x 之间具有线性相关关系.
(Ⅰ)求生产成本 y 关于蛋白质含量 x 的回归方程;
(Ⅱ)根据(Ⅰ)的结果,若公司准备将生产成本提高到 60至 70 元,则判断生产的乳制品蛋
白质含量的取值范围.(精确到小数点后两位)
n
(xi x)(yi y)
参考公式:b i 1 .
n
(xi x)
2
i 1
7 7
参考数据: x 1.68, (xi x)
2 6.79, (xi x)(yi y) 81.41.
i 1 i 1
19.(本小题 12 分)函数 f (x) ex (x2 ax a) .
(Ⅰ)若 x 1是函数 f (x)的极值点,求 a 的值,并判断 x 1是极大值点还是极小值点;
(Ⅱ)求函数 f (x)的单调区间.
第 3 页,共 4 页
20.(本小题 12 分)在四棱锥 P ABCD 中,底面 ABCD 为矩形, PAB 为边长为 2 的正三角形,且
平面 PAB 平面 ABCD,E 为线段 AD 的中点,PE 与平面 ABCD 所成角为 45 .
(Ⅰ)证明: EP EC ;
(Ⅱ)求证:平面 PCE 平面 PBC . P
F
B C
A E D
21.(本小题 12 分)已知过点 (0,2)的直线与抛物线 x2 4y 相交于 A, B 两点,M 为线段 AB 的中点,
过 M 作 x 轴的垂线与抛物线交于点 N.
(1)若抛物线在 N 点处的切线的斜率等于 2,求直线 AB 的方程;
(2)设 D(0,11) ,求 DAB 与 NAB面积之差的最大值.
1 1
22.(本小题 12 分)函数 f (x) ln x ax2 (a 2)x a 3,其中 a 1.
2 2
(Ⅰ)若函数 f (x)在区间[x1, x2 ]上单调递减,求 x2 x 的最大值; 1
(Ⅱ)曲线 C: y f (x)在 (1,1) 处的切线为 l ,若直线 l 与曲线 C 有且仅有一个公共点,求 a 满足的
条件.
第 4 页,共 4 页
2022~2023 学年度下期高 2024 届半期考试
数学试卷(文科)(参考答案)
一、选择题(每小题 5分,共 60分)
BCADB ADCDB AC
二、填空题(每小题 5 分,共 20 分)
13. i 14. 2 3 15. (0,+ ) 16.①③④
三、解答题(共 70 分)
17.解:(Ⅰ)由 2 = x2 + y2 , cos = x, ……………2 分
得: x2 + y2 = 4x 3 ,
所以曲线 C 的直角坐标方程为 (x 2)2 + y2 =1, ……………5 分
(Ⅱ)设 B( , ) ,则由题意可知 A(2 , ) ,
4
2 = 8 cos 3
将 A,B 坐标代入方程 2 = 4 cos 3得: ,
2
= 4 cos 3
2 6 4 2 2 = 3,得 = , ……………8 分
2
6
B 的极径为 . ……………10 分
2
18.解:(Ⅰ)由题中数据可得 y = 42, ……………2分
设生产成本 y 关于蛋白质含量 x 的回归方程为 y = b x + a ,
7
(xi x)(yi y) 81.41
b = i=1 = =11.99, ……………4分
7 6.79
(xi x)
2
i=1
a = y b x = 42 11.99 1.68 = 21.86 ,
所以回归方程为 y =11.99x + 21.86, ……………6分
(Ⅱ)当 y = 60 时,由(1)得11.99x + 21.86 = 60.
解得 x 3.18, ……………8分
当 y = 70 时,由(1)得11.99x + 21.86 = 70.
解得 x 4.02 , ……………10分
所以生产的乳制品蛋白质含量的取值范围为[3.18,4.02] . ……………12分
19.解:(Ⅰ) f / (x) = ex (x2 ax a + 2x a) = ex (x + 2)(x a),
x =1是函数 f (x) 的极值点,
y = kx + 2
联立 x
2 4kx 8 = 0 , x + x = 4k, x x = 8, …………2 分
2 1 2 1 2
x = 4y
N (2k,k 2 ) , …………3 分
x2 x
函数 y = 的导函数为 y / = ,
4 2
2k
所以抛物线在 N 点处的切线的斜率为 ,
2
2k
= 2,即 k =1
2
l ; …………5 分 AB : y = x+ 2
(2)由(1)问可得 | AB |= 1+ k 2 16k 2 +32 ,
| k 2 + 2 |
点 N (2k, k 2 ) 到直线 AB 的距离为 ,
1+ k 2
9
点 D(0,11)到直线 AB 的距离为 ,
1+ k 2
S = S S =18 k 2 + 2 2 k 2 + 2 (k 2 + 2) , …………8 分 DAB NAB
令 t = k 2 + 2 2 ,
S =18t 2t3 ,令函数 f (t) =18t 2t3
f / (t) =18 6t 2 = 6(3 t 2 ),
所以函数 f (t)在区间[ 2, 3]上递增,在 [ 3,+ )上递减,
t = 3,即 k = 1时, DAB 与 NAB面积之差取得最大值12 3 .…………12 分
2
22.解:(Ⅰ) f /
1 ax (a + 2)x +1
(x) = + ax (a + 2) = ,
x x
= (a + 2)2 4a = a2 + 4 0 ,且 a 1,
ax2 (a + 2)x +1= 0 在 (0,+ ) 上有两个不同的根 x1, x , 2
据题可得 ax2 (a + 2)x +1 0 的解集为[x1, x , 2 ]
2 1
x1 + x2 =1+ , x1x2 = ,
a a
4
x2 x1 = (x + x
2
1 2 ) 4x1x2 = 1+ 5
a2
所以 x x 的最大值为2 1 5 .
(Ⅱ) f / (1) = 1,
所以直线 l : y = x+ 2,
又直线 l 与曲线 C 有且仅有一个公共点,
1 1
ln x + ax2 (a + 2)x + a +3 = x + 2 在 (0,+ ) 上有唯一根 x =1
2 2
1 1
令函数 g(x) = ln x + ax2 (a +1)x + a +1,
2 2
1 ax2/ (a +1)x +1 (x 1)(ax 1)g (x) = + ax (a +1) = = ,
x x x
当 a =1时,函数 g(x)在 (0,+ ) 上单调递增,且 g(1) = 0,满足条件,
1 1
当 a 1时,函数 g(x)在 (0, ) 上单调递增,在 ( ,1)上单调递减,在 (1,+ )上单调递增,
a a
1
当 x → 0时, g(x) → ,所以 x0 (0, ) ,使 g(x ) = 0,所以不满足条件, 0
a
综上得 a 满足的条件为 a =1.
数学试卷(文科)
考试时长:120分钟 满分:150分
一、选择题(每小题 5 分,共 60 分)
1.已知复数 z (m 1) (m 1)i, (m R)为纯虚数,则实数 m 的值为( )
(A) 1 (B)1 (C) 0 (D)1或 1
2.在极坐标系中,以极点为圆心,1 为半径的圆的极坐标方程为( )
(A) cos 1 (B) sin 1 (C) 1 (D)
4
3.利用分析法证明不等式M N 成立,只需证明 P N 成立即可,则“ P N 成立”是“M N 成
立”的( )
(A)充分条件 (B)必要条件 (C)充要条件 (D)既不充分也不必要
4.已知 (x 是圆 20 , y0 ) x y
2 r2 上一点,则直线 x0x y
2 与圆 2 2
0 y r x y r
2 相切,且 (x , y ) 为切点,0 0
x2 y2
类似的,点 (x0 , y 是椭圆0 ) 1(a b 0)上一点,则以 (x0 , y ) 为切点,与椭圆相切的切线方程 2 2 0a b
为( )
x x y y x x y y
(A) x0x y y 1 (B)0 x0x y y a
2b2 (C) 0 0 1 (D) 0 00 1
a2 b2 a2 b2
5.已知复数 z x yi, (x, y R)对应的点在第一象限,z 的实部和虚部分别是双曲线 C 的实轴长和虚
轴长,若 | z | 4 ,则双曲线 C 的焦距为( )
(A)8 (B) 4 (C) 2 2 (D) 2
x2
6.函数 f (x) 的大致图像为( )
ex
y y y y
O x O x O x O x
(A) (B) (C) (D)
7.已知函数 f (x) x3 f / (1)x2 ,则 f / (1) ( )
3 3
(A) (B) (C)3 (D) 3
2 2
x / 4x
8.将圆 x2 y2 1经过坐标变换 : 后得到的曲线方程为( )
/
y 2y
第 1 页,共 4 页
第 2 页,共 4 页
三、解答题(共 70 分)
17.(本小题 10 分)已知曲线 C 的极坐标方程为 2 4 cos 3,A, B 是曲线 C 上不同的两点,且
OA 2OB,其中O 为极点.
(Ⅰ)求曲线 C 的直角坐标方程;
(Ⅱ)求点 B 的极径.
18.(本小题 12 分)某企业生产的某种乳制品的蛋白质含量 x(%)与生产成本 y(元)之间的数据
如下表:
x 0 0.69 1.39 1.79 2.40 2.56 2.94
y 19 32 40 44 52 53 54
已知生产成本 y 与产品蛋白质含量 x 之间具有线性相关关系.
(Ⅰ)求生产成本 y 关于蛋白质含量 x 的回归方程;
(Ⅱ)根据(Ⅰ)的结果,若公司准备将生产成本提高到 60至 70 元,则判断生产的乳制品蛋
白质含量的取值范围.(精确到小数点后两位)
n
(xi x)(yi y)
参考公式:b i 1 .
n
(xi x)
2
i 1
7 7
参考数据: x 1.68, (xi x)
2 6.79, (xi x)(yi y) 81.41.
i 1 i 1
19.(本小题 12 分)函数 f (x) ex (x2 ax a) .
(Ⅰ)若 x 1是函数 f (x)的极值点,求 a 的值,并判断 x 1是极大值点还是极小值点;
(Ⅱ)求函数 f (x)的单调区间.
第 3 页,共 4 页
20.(本小题 12 分)在四棱锥 P ABCD 中,底面 ABCD 为矩形, PAB 为边长为 2 的正三角形,且
平面 PAB 平面 ABCD,E 为线段 AD 的中点,PE 与平面 ABCD 所成角为 45 .
(Ⅰ)证明: EP EC ;
(Ⅱ)求证:平面 PCE 平面 PBC . P
F
B C
A E D
21.(本小题 12 分)已知过点 (0,2)的直线与抛物线 x2 4y 相交于 A, B 两点,M 为线段 AB 的中点,
过 M 作 x 轴的垂线与抛物线交于点 N.
(1)若抛物线在 N 点处的切线的斜率等于 2,求直线 AB 的方程;
(2)设 D(0,11) ,求 DAB 与 NAB面积之差的最大值.
1 1
22.(本小题 12 分)函数 f (x) ln x ax2 (a 2)x a 3,其中 a 1.
2 2
(Ⅰ)若函数 f (x)在区间[x1, x2 ]上单调递减,求 x2 x 的最大值; 1
(Ⅱ)曲线 C: y f (x)在 (1,1) 处的切线为 l ,若直线 l 与曲线 C 有且仅有一个公共点,求 a 满足的
条件.
第 4 页,共 4 页
2022~2023 学年度下期高 2024 届半期考试
数学试卷(文科)(参考答案)
一、选择题(每小题 5分,共 60分)
BCADB ADCDB AC
二、填空题(每小题 5 分,共 20 分)
13. i 14. 2 3 15. (0,+ ) 16.①③④
三、解答题(共 70 分)
17.解:(Ⅰ)由 2 = x2 + y2 , cos = x, ……………2 分
得: x2 + y2 = 4x 3 ,
所以曲线 C 的直角坐标方程为 (x 2)2 + y2 =1, ……………5 分
(Ⅱ)设 B( , ) ,则由题意可知 A(2 , ) ,
4
2 = 8 cos 3
将 A,B 坐标代入方程 2 = 4 cos 3得: ,
2
= 4 cos 3
2 6 4 2 2 = 3,得 = , ……………8 分
2
6
B 的极径为 . ……………10 分
2
18.解:(Ⅰ)由题中数据可得 y = 42, ……………2分
设生产成本 y 关于蛋白质含量 x 的回归方程为 y = b x + a ,
7
(xi x)(yi y) 81.41
b = i=1 = =11.99, ……………4分
7 6.79
(xi x)
2
i=1
a = y b x = 42 11.99 1.68 = 21.86 ,
所以回归方程为 y =11.99x + 21.86, ……………6分
(Ⅱ)当 y = 60 时,由(1)得11.99x + 21.86 = 60.
解得 x 3.18, ……………8分
当 y = 70 时,由(1)得11.99x + 21.86 = 70.
解得 x 4.02 , ……………10分
所以生产的乳制品蛋白质含量的取值范围为[3.18,4.02] . ……………12分
19.解:(Ⅰ) f / (x) = ex (x2 ax a + 2x a) = ex (x + 2)(x a),
x =1是函数 f (x) 的极值点,
y = kx + 2
联立 x
2 4kx 8 = 0 , x + x = 4k, x x = 8, …………2 分
2 1 2 1 2
x = 4y
N (2k,k 2 ) , …………3 分
x2 x
函数 y = 的导函数为 y / = ,
4 2
2k
所以抛物线在 N 点处的切线的斜率为 ,
2
2k
= 2,即 k =1
2
l ; …………5 分 AB : y = x+ 2
(2)由(1)问可得 | AB |= 1+ k 2 16k 2 +32 ,
| k 2 + 2 |
点 N (2k, k 2 ) 到直线 AB 的距离为 ,
1+ k 2
9
点 D(0,11)到直线 AB 的距离为 ,
1+ k 2
S = S S =18 k 2 + 2 2 k 2 + 2 (k 2 + 2) , …………8 分 DAB NAB
令 t = k 2 + 2 2 ,
S =18t 2t3 ,令函数 f (t) =18t 2t3
f / (t) =18 6t 2 = 6(3 t 2 ),
所以函数 f (t)在区间[ 2, 3]上递增,在 [ 3,+ )上递减,
t = 3,即 k = 1时, DAB 与 NAB面积之差取得最大值12 3 .…………12 分
2
22.解:(Ⅰ) f /
1 ax (a + 2)x +1
(x) = + ax (a + 2) = ,
x x
= (a + 2)2 4a = a2 + 4 0 ,且 a 1,
ax2 (a + 2)x +1= 0 在 (0,+ ) 上有两个不同的根 x1, x , 2
据题可得 ax2 (a + 2)x +1 0 的解集为[x1, x , 2 ]
2 1
x1 + x2 =1+ , x1x2 = ,
a a
4
x2 x1 = (x + x
2
1 2 ) 4x1x2 = 1+ 5
a2
所以 x x 的最大值为2 1 5 .
(Ⅱ) f / (1) = 1,
所以直线 l : y = x+ 2,
又直线 l 与曲线 C 有且仅有一个公共点,
1 1
ln x + ax2 (a + 2)x + a +3 = x + 2 在 (0,+ ) 上有唯一根 x =1
2 2
1 1
令函数 g(x) = ln x + ax2 (a +1)x + a +1,
2 2
1 ax2/ (a +1)x +1 (x 1)(ax 1)g (x) = + ax (a +1) = = ,
x x x
当 a =1时,函数 g(x)在 (0,+ ) 上单调递增,且 g(1) = 0,满足条件,
1 1
当 a 1时,函数 g(x)在 (0, ) 上单调递增,在 ( ,1)上单调递减,在 (1,+ )上单调递增,
a a
1
当 x → 0时, g(x) → ,所以 x0 (0, ) ,使 g(x ) = 0,所以不满足条件, 0
a
综上得 a 满足的条件为 a =1.
同课章节目录
