【2023中考二轮复习】直角三角形的存在性问题专题探究(含解析)
文档属性
| 名称 | 【2023中考二轮复习】直角三角形的存在性问题专题探究(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 14:53:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年中考复习存在性问题系列
直角三角形的存在性问题专题探究
直角三角形存在性问题主要是已知直角三角形的一边(即直角三角形的两个点确定),求解第三点。这类问题主要是和动点问题结合在一起,主要在于考查学生的探寻能力和分类研究的推理能力,也是近几年来各市地对学生能力提高方面的一个考查。
解题攻略
构造直角三角形的一般思路:
构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆.
动点产生的直角三角形的一般解法,以三角形ABC为直角三角形为例
代数法
(1)列出A、B、C的坐标,动点用参数表示;
(2)列出线段AB、AC、BC长度的平方;
(3)分类列方程:①,②,③;
2、几何法
(1)两线一圆得坐标
①若∠A为直角,过点A作AB的垂线,与x轴的交点即为所求点C;
②若∠B为直角,过点B作AB的垂线,与x轴的交点即为所求点C;
③若∠C为直角,以AB为直径作圆,与x轴的交点即为所求点C.(直径所对的圆周角为直角)
重点还是如何求得点坐标,求法相同,以为例:
(2)构造三垂直
利用到一线等三角之K字(90°)类型和母子相似型类型,尝试建构相应的相似来进行处理;
构造三垂直步骤:
第一步:过直角顶点作一条水平或竖直的直线;
第二步:过另外两端点向该直线作垂线,即可得三垂直相似.
(3)利用对应边成比例求线段,必要时可设未知数列方程求解
3、解析法
两条直线互相垂直的条件,即k1k2 =-1来解决.
解题类型及其思路
当直角三角形存在时可从三个角度进行分析研究:
当动点在直线上运动时,常用的方法是① ,②三角形相似,③勾股定理;(2)当动点在曲线上运动时,情况分类如下,第一当已知点处作直角的方法① ,②三角形相似,③勾股定理;第二是当动点处作直角的方法:寻找特殊角。
典例剖析
1.动点在直线上运动
例1.如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
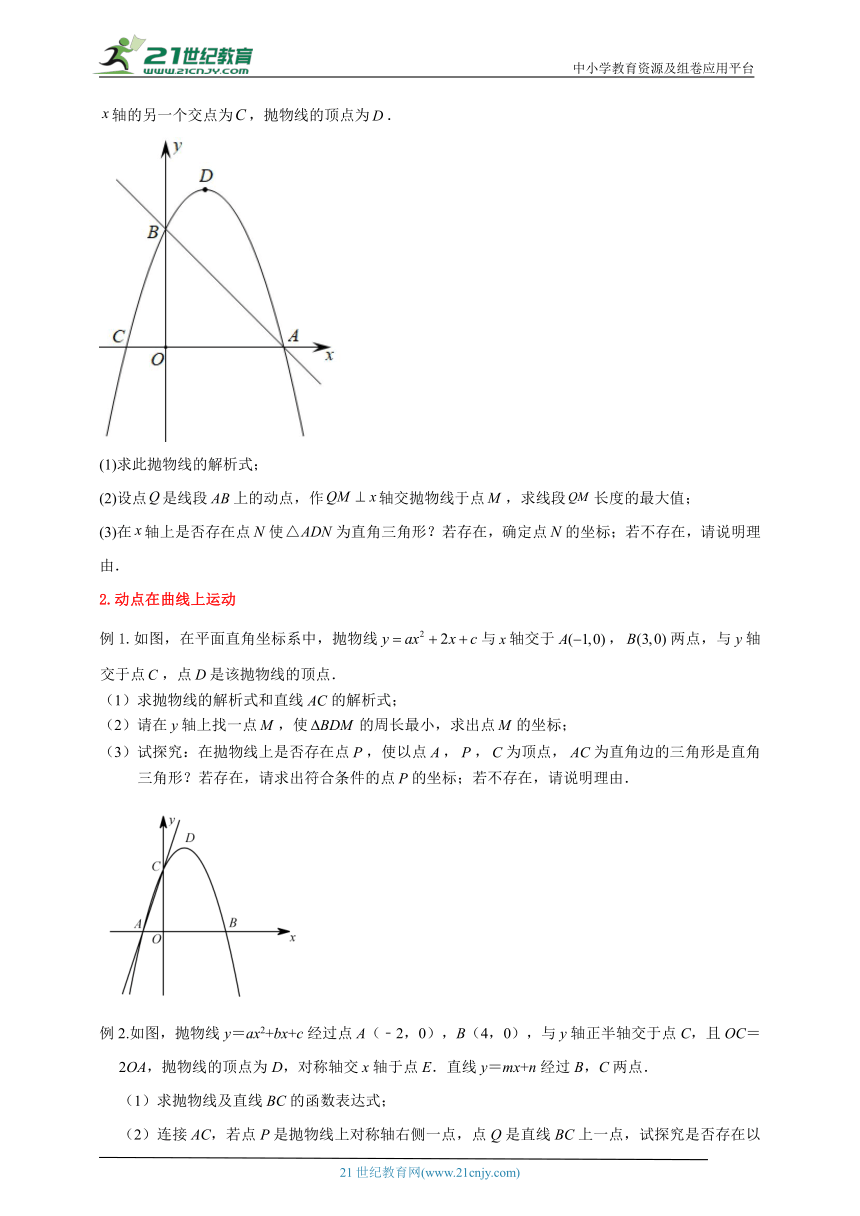
例2.已知,如图,抛物线经过直线与坐标轴的两个交点,,此抛物线与轴的另一个交点为,抛物线的顶点为.
(1)求此抛物线的解析式;
(2)设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值;
(3)在轴上是否存在点使为直角三角形?若存在,确定点的坐标;若不存在,请说明理由.
2.动点在曲线上运动
例1.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的解析式和直线的解析式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在拋物线上是否存在点,使以点,,为顶点,为直角边的三角形是直角三角形?若存在,请求出符合条件的点的坐标;若不存在,请说明理由.
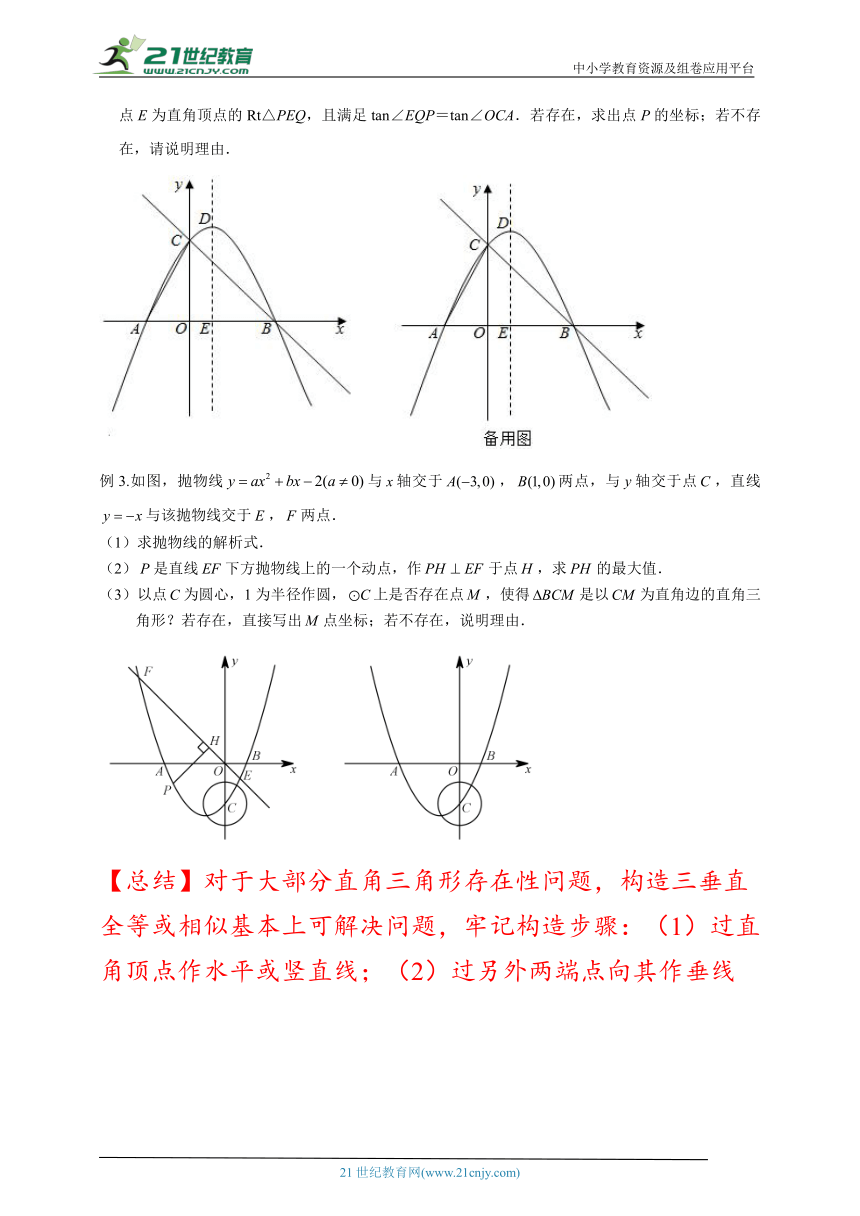
例2.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是否存在以点E为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.
例3.如图,抛物线与轴交于,两点,与轴交于点,直线与该抛物线交于,两点.
(1)求抛物线的解析式.
(2)是直线下方抛物线上的一个动点,作于点,求的最大值.
(3)以点为圆心,1为半径作圆,上是否存在点,使得是以为直角边的直角三角形?若存在,直接写出点坐标;若不存在,说明理由.
【总结】对于大部分直角三角形存在性问题,构造三垂直全等或相似基本上可解决问题,牢记构造步骤:(1)过直角顶点作水平或竖直线;(2)过另外两端点向其作垂线
2023年中考复习存在性问题系列
直角三角形的存在性问题专题探究(解析版)
典例剖析
1.动点在直线上运动
例1.如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)∵抛物线y=ax2+bx+3过点A(3,0),B(﹣1,0),
∴ 解得:,
∴这条抛物线对应的函数表达式为y=﹣x2+2x+3.
(2)用勾股定理
在y轴上存在点P,使得△PAM为直角三角形.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4),
∴AM2=(3﹣1)2+42=20,
设点P坐标为(0,p),
∴AP2=32+p2=9+p2,MP2=12+(4﹣p)2=17﹣8p+p2,
①若∠PAM=90°,则AM2+AP2=MP2,
∴20+9+p2=17﹣8p+p2,
解得:p=﹣,
∴P(0,﹣).
②若∠APM=90°,则AP2+MP2=AM2,
∴9+p2+17﹣8p+p2=20,
解得:p1=1,p2=3,
∴P(0,1)或(0,3).
③若∠AMP=90°,则AM2+MP2=AP2,
∴20+17﹣8p+p2=9+p2,
解得:p=,
∴P(0,).
综上所述,点P坐标为(0,﹣)或(0,1)或(0,3)或(0,)时,△PAM为直角三角形.
例2.已知,如图,抛物线经过直线与坐标轴的两个交点,,此抛物线与轴的另一个交点为,抛物线的顶点为.
(1)求此抛物线的解析式;
(2)设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值;
(3)在轴上是否存在点使为直角三角形?若存在,确定点的坐标;若不存在,请说明理由.
(1)解:∵直线与坐标轴的两个交点,,
∴,,
∵抛物线经过直线与坐标轴的两个交点,,
∴根据题意可得方程:
∴,
∴二次函数的解析式为:.
(2)解:∵点经过抛物线
∴设点,
∵是线段上的动点,
∴,
∴
∴的最大值为.
用相似三角形解
解:①当时,如图所示
∵时,
∴,
∵,
∴,
∵,,
∴,
②当时,则,
∴,
∴,
∵,
即,
解得:
∵,
∴,
综上所述点的坐标为:或
【点睛】本题考查了二次函数的应用,掌握二次函数的性质,待定系数法,熟记数轴上两点之间的距离公式运用相似三角形知识是解题的关键.
2.动点在曲线上运动
例1.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的解析式和直线的解析式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在拋物线上是否存在点,使以点,,为顶点,为直角边的三角形是直角三角形?若存在,请求出符合条件的点的坐标;若不存在,请说明理由.
解:(1)抛物线:,直线AC:y=3x+3;
(2)看图,M点坐标为(0,3)与C点重合了.
(3)考虑到AC为直角边,故分别过A、C作AC的垂线,与抛物线交点即为所求P点,
有如下两种情况,
先求过A点所作垂线得到的点P:
设P点坐标为,
则PM=m+1,AM=,
易证△PMA∽△ANC,且AN=3,CN=1,
∴,解得:,(舍),
故第1个P点坐标为;
再求过点C所作垂线得到的点P:
,CN=m,
,解得:,(舍),
故第2个P点坐标为.
综上所述,P点坐标为或.
例2.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是否存在以点E为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)由点A的坐标知,OA=2,
∵OC=2OA=4,故点C的坐标为(0,4),
将点A、B、C的坐标代入抛物线表达式得:,解得,
故抛物线的表达式为y=﹣x+x+4;
将点B、C的坐标代入一次函数表达式得:,解得,
故直线BC的表达式为y=﹣x+4;
(2)存在,理由:
设点P的坐标为(m,﹣m2+m+4)、点Q的坐标为(t,﹣t+4),
①当点Q在点P的左侧时,
如图2,过点P、Q分别作x轴的垂线,垂足分别为N、M,
由题意得:∠PEQ=90°,
∴∠PEN+∠QEM=90°,
∵∠EQM+∠QEM=90°,
∴∠PEN=∠EQM,
∴∠QME=∠ENP=90°,
∴△QME∽△ENP,
∴=tan∠EQP=tan∠OCA===,
则PN=﹣m2+m+4,ME=1﹣t,EN=m﹣1,QM=﹣t+4,
∴==,
解得m=±(舍去负值),
当m=时,﹣m2+m+4=,
故点P的坐标为(,).
②当点Q在点P的右侧时,
分别过点P、Q作抛物线对称轴的垂线,垂足分别为N、M,
则MQ=t﹣1,ME=t﹣4,NE=﹣m2+m+4、PN=m﹣1,
同理可得:△QME∽△ENP,
∴=tan∠PQE=2,
即,
解得m=(舍去负值),
故m=,
故点P的坐标为(,),
故点P的坐标为(,)或(,).
例3.如图,抛物线与轴交于,两点,与轴交于点,直线与该抛物线交于,两点.
(1)求抛物线的解析式.
(2)是直线下方抛物线上的一个动点,作于点,求的最大值.
(3)以点为圆心,1为半径作圆,上是否存在点,使得是以为直角边的直角三角形?若存在,直接写出点坐标;若不存在,说明理由.
解(1);
(2)过点P作x轴的垂线交EF于点Q,所谓PH最大,即PQ最大,易解.
(3)CM为直角边,故点C可能为直角顶点,点M也可能为直角顶点.
①当为直角时,如图:
:不难求得CF=1,BF=2,
∴,又,
可得:,.
故坐标为;
同理可求坐标为.
②当∠BMC为直角时,如图:
:不难发现CM=1,BC=,∴,
即△MEC∽△BFM,且相似比为1:2,
设EC=a,EM=b,则FM=2a,BF=2b,
由图可知:,解得:.
故点的坐标为.
至于坐标,显然.
综上所述,M点坐标为或或或
【总结】对于大部分直角三角形存在性问题,构造三垂直全等或相似基本上可解决问题,牢记构造步骤:(1)过直角顶点作水平或竖直线;(2)过另外两端点向其作垂线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023年中考复习存在性问题系列
直角三角形的存在性问题专题探究
直角三角形存在性问题主要是已知直角三角形的一边(即直角三角形的两个点确定),求解第三点。这类问题主要是和动点问题结合在一起,主要在于考查学生的探寻能力和分类研究的推理能力,也是近几年来各市地对学生能力提高方面的一个考查。
解题攻略
构造直角三角形的一般思路:
构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆.
动点产生的直角三角形的一般解法,以三角形ABC为直角三角形为例
代数法
(1)列出A、B、C的坐标,动点用参数表示;
(2)列出线段AB、AC、BC长度的平方;
(3)分类列方程:①,②,③;
2、几何法
(1)两线一圆得坐标
①若∠A为直角,过点A作AB的垂线,与x轴的交点即为所求点C;
②若∠B为直角,过点B作AB的垂线,与x轴的交点即为所求点C;
③若∠C为直角,以AB为直径作圆,与x轴的交点即为所求点C.(直径所对的圆周角为直角)
重点还是如何求得点坐标,求法相同,以为例:
(2)构造三垂直
利用到一线等三角之K字(90°)类型和母子相似型类型,尝试建构相应的相似来进行处理;
构造三垂直步骤:
第一步:过直角顶点作一条水平或竖直的直线;
第二步:过另外两端点向该直线作垂线,即可得三垂直相似.
(3)利用对应边成比例求线段,必要时可设未知数列方程求解
3、解析法
两条直线互相垂直的条件,即k1k2 =-1来解决.
解题类型及其思路
当直角三角形存在时可从三个角度进行分析研究:
当动点在直线上运动时,常用的方法是① ,②三角形相似,③勾股定理;(2)当动点在曲线上运动时,情况分类如下,第一当已知点处作直角的方法① ,②三角形相似,③勾股定理;第二是当动点处作直角的方法:寻找特殊角。
典例剖析
1.动点在直线上运动
例1.如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
例2.已知,如图,抛物线经过直线与坐标轴的两个交点,,此抛物线与轴的另一个交点为,抛物线的顶点为.
(1)求此抛物线的解析式;
(2)设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值;
(3)在轴上是否存在点使为直角三角形?若存在,确定点的坐标;若不存在,请说明理由.
2.动点在曲线上运动
例1.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的解析式和直线的解析式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在拋物线上是否存在点,使以点,,为顶点,为直角边的三角形是直角三角形?若存在,请求出符合条件的点的坐标;若不存在,请说明理由.
例2.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是否存在以点E为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.
例3.如图,抛物线与轴交于,两点,与轴交于点,直线与该抛物线交于,两点.
(1)求抛物线的解析式.
(2)是直线下方抛物线上的一个动点,作于点,求的最大值.
(3)以点为圆心,1为半径作圆,上是否存在点,使得是以为直角边的直角三角形?若存在,直接写出点坐标;若不存在,说明理由.
【总结】对于大部分直角三角形存在性问题,构造三垂直全等或相似基本上可解决问题,牢记构造步骤:(1)过直角顶点作水平或竖直线;(2)过另外两端点向其作垂线
2023年中考复习存在性问题系列
直角三角形的存在性问题专题探究(解析版)
典例剖析
1.动点在直线上运动
例1.如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)∵抛物线y=ax2+bx+3过点A(3,0),B(﹣1,0),
∴ 解得:,
∴这条抛物线对应的函数表达式为y=﹣x2+2x+3.
(2)用勾股定理
在y轴上存在点P,使得△PAM为直角三角形.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4),
∴AM2=(3﹣1)2+42=20,
设点P坐标为(0,p),
∴AP2=32+p2=9+p2,MP2=12+(4﹣p)2=17﹣8p+p2,
①若∠PAM=90°,则AM2+AP2=MP2,
∴20+9+p2=17﹣8p+p2,
解得:p=﹣,
∴P(0,﹣).
②若∠APM=90°,则AP2+MP2=AM2,
∴9+p2+17﹣8p+p2=20,
解得:p1=1,p2=3,
∴P(0,1)或(0,3).
③若∠AMP=90°,则AM2+MP2=AP2,
∴20+17﹣8p+p2=9+p2,
解得:p=,
∴P(0,).
综上所述,点P坐标为(0,﹣)或(0,1)或(0,3)或(0,)时,△PAM为直角三角形.
例2.已知,如图,抛物线经过直线与坐标轴的两个交点,,此抛物线与轴的另一个交点为,抛物线的顶点为.
(1)求此抛物线的解析式;
(2)设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值;
(3)在轴上是否存在点使为直角三角形?若存在,确定点的坐标;若不存在,请说明理由.
(1)解:∵直线与坐标轴的两个交点,,
∴,,
∵抛物线经过直线与坐标轴的两个交点,,
∴根据题意可得方程:
∴,
∴二次函数的解析式为:.
(2)解:∵点经过抛物线
∴设点,
∵是线段上的动点,
∴,
∴
∴的最大值为.
用相似三角形解
解:①当时,如图所示
∵时,
∴,
∵,
∴,
∵,,
∴,
②当时,则,
∴,
∴,
∵,
即,
解得:
∵,
∴,
综上所述点的坐标为:或
【点睛】本题考查了二次函数的应用,掌握二次函数的性质,待定系数法,熟记数轴上两点之间的距离公式运用相似三角形知识是解题的关键.
2.动点在曲线上运动
例1.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的解析式和直线的解析式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在拋物线上是否存在点,使以点,,为顶点,为直角边的三角形是直角三角形?若存在,请求出符合条件的点的坐标;若不存在,请说明理由.
解:(1)抛物线:,直线AC:y=3x+3;
(2)看图,M点坐标为(0,3)与C点重合了.
(3)考虑到AC为直角边,故分别过A、C作AC的垂线,与抛物线交点即为所求P点,
有如下两种情况,
先求过A点所作垂线得到的点P:
设P点坐标为,
则PM=m+1,AM=,
易证△PMA∽△ANC,且AN=3,CN=1,
∴,解得:,(舍),
故第1个P点坐标为;
再求过点C所作垂线得到的点P:
,CN=m,
,解得:,(舍),
故第2个P点坐标为.
综上所述,P点坐标为或.
例2.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是否存在以点E为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)由点A的坐标知,OA=2,
∵OC=2OA=4,故点C的坐标为(0,4),
将点A、B、C的坐标代入抛物线表达式得:,解得,
故抛物线的表达式为y=﹣x+x+4;
将点B、C的坐标代入一次函数表达式得:,解得,
故直线BC的表达式为y=﹣x+4;
(2)存在,理由:
设点P的坐标为(m,﹣m2+m+4)、点Q的坐标为(t,﹣t+4),
①当点Q在点P的左侧时,
如图2,过点P、Q分别作x轴的垂线,垂足分别为N、M,
由题意得:∠PEQ=90°,
∴∠PEN+∠QEM=90°,
∵∠EQM+∠QEM=90°,
∴∠PEN=∠EQM,
∴∠QME=∠ENP=90°,
∴△QME∽△ENP,
∴=tan∠EQP=tan∠OCA===,
则PN=﹣m2+m+4,ME=1﹣t,EN=m﹣1,QM=﹣t+4,
∴==,
解得m=±(舍去负值),
当m=时,﹣m2+m+4=,
故点P的坐标为(,).
②当点Q在点P的右侧时,
分别过点P、Q作抛物线对称轴的垂线,垂足分别为N、M,
则MQ=t﹣1,ME=t﹣4,NE=﹣m2+m+4、PN=m﹣1,
同理可得:△QME∽△ENP,
∴=tan∠PQE=2,
即,
解得m=(舍去负值),
故m=,
故点P的坐标为(,),
故点P的坐标为(,)或(,).
例3.如图,抛物线与轴交于,两点,与轴交于点,直线与该抛物线交于,两点.
(1)求抛物线的解析式.
(2)是直线下方抛物线上的一个动点,作于点,求的最大值.
(3)以点为圆心,1为半径作圆,上是否存在点,使得是以为直角边的直角三角形?若存在,直接写出点坐标;若不存在,说明理由.
解(1);
(2)过点P作x轴的垂线交EF于点Q,所谓PH最大,即PQ最大,易解.
(3)CM为直角边,故点C可能为直角顶点,点M也可能为直角顶点.
①当为直角时,如图:
:不难求得CF=1,BF=2,
∴,又,
可得:,.
故坐标为;
同理可求坐标为.
②当∠BMC为直角时,如图:
:不难发现CM=1,BC=,∴,
即△MEC∽△BFM,且相似比为1:2,
设EC=a,EM=b,则FM=2a,BF=2b,
由图可知:,解得:.
故点的坐标为.
至于坐标,显然.
综上所述,M点坐标为或或或
【总结】对于大部分直角三角形存在性问题,构造三垂直全等或相似基本上可解决问题,牢记构造步骤:(1)过直角顶点作水平或竖直线;(2)过另外两端点向其作垂线
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
