9.3.1用相同的正多边形铺设地面 课件(共30张PPT)
文档属性
| 名称 | 9.3.1用相同的正多边形铺设地面 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
9.3.1用相同的正多边形铺设地面
华师大版 七年级 下册
教学目标
教学目标:1.通过用相同的正多边形拼地板的活动,巩固多边形的内角和
与外角和公式.
2.通过“拼地板”和相关计算,使学生从中发现能拼成一个不
留空隙,又不重叠的平面图形的关键是几个多边形的内角
和相加要等于360°.
教学重点:通过用相同的正多边形拼地板活动,巩固多边形的内角和与外角和公式.教学难点:探索用各种正多边形拼地板的过程和原理.
新知导入
情境引入
图片欣赏
思考:
用同一种正多边形铺地板,哪些能密铺不留空隙呢
铺地板的学问
新知讲解
合作学习
新课探索
围绕某一顶点铺满地面
既不留下一丝空白,又不相互重叠这叫做“平面镶嵌”“密铺”或者“满铺”.
用同一种正多边形铺地板,哪些能密铺不留空隙呢
探索
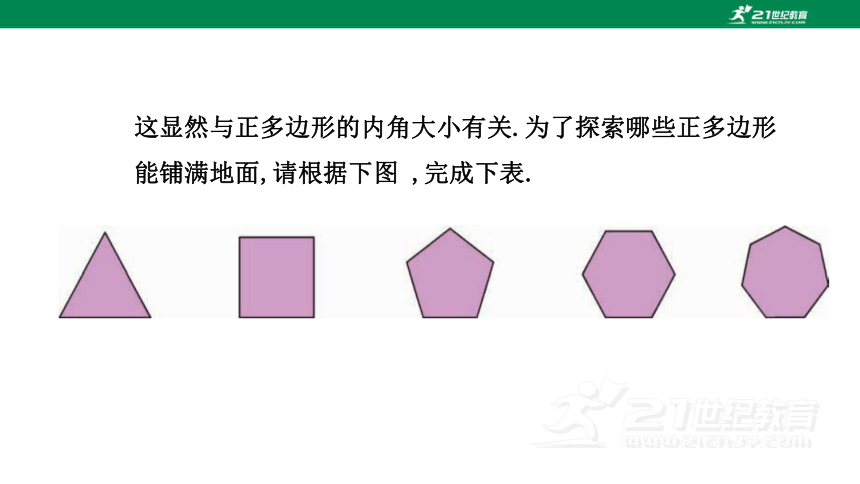
这显然与正多边形的内角大小有关.
这显然与正多边形的内角大小有关.为了探索哪些正多边形能铺满地面,请根据下图 ,完成下表.
正多边形的边数 3 4 5 6 7 … n
正多边形的内角和 180° 360° …
每个内角的度数 60° 90° …
108°
720°
540°
1080°
(n-2) · 180°
120°
135°
60°
60°
60°
60°
60°
60°
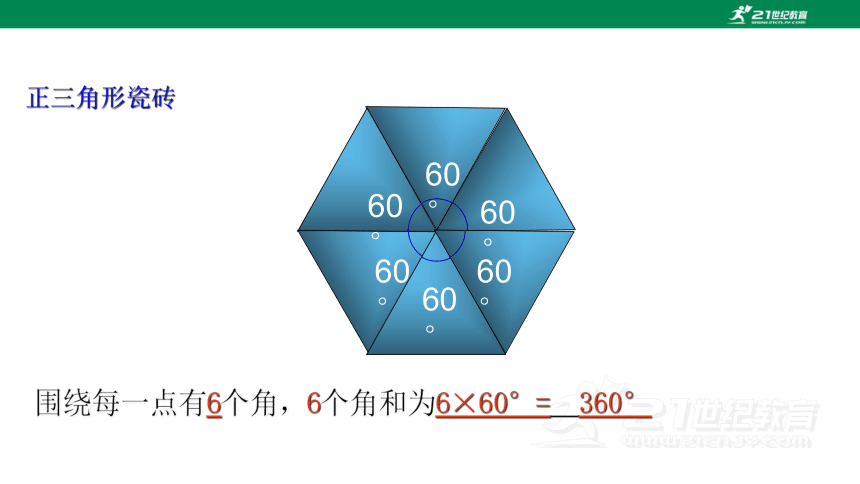
正三角形瓷砖
围绕每一点有6个角,6个角和为6×60°= 360°
90°
90°
90°
90°
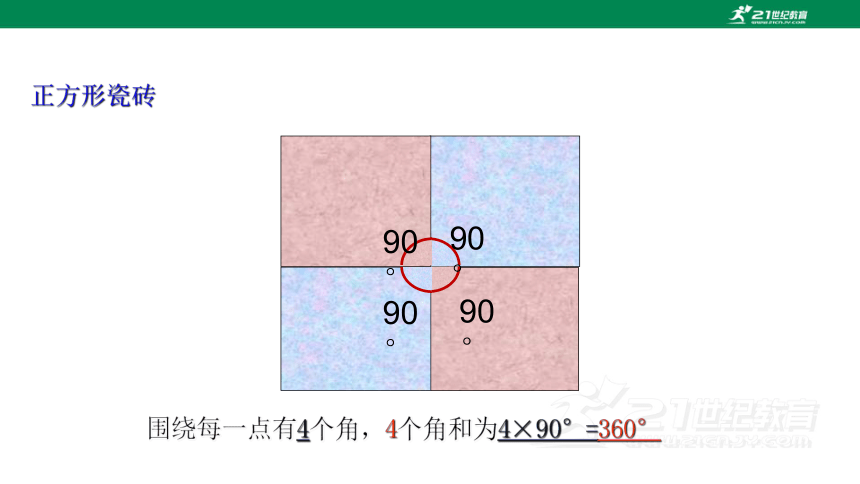
正方形瓷砖
围绕每一点有4个角,4个角和为4×90°=360°
108°
108°
108°
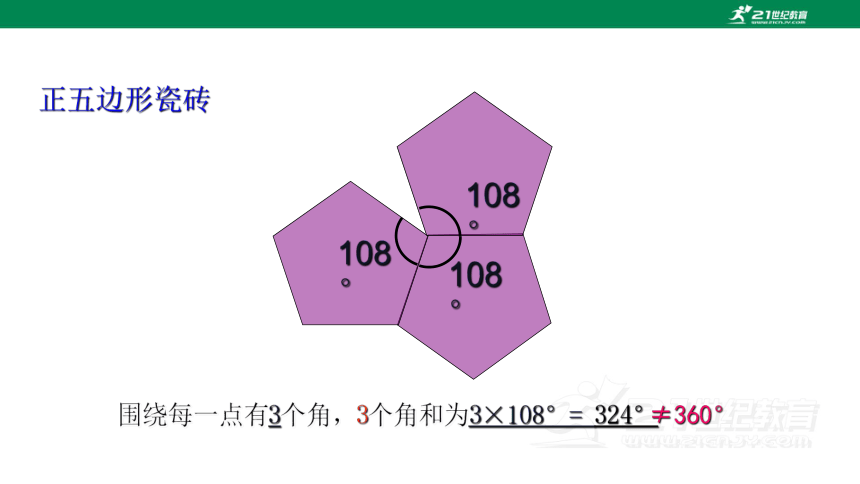
正五边形瓷砖
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
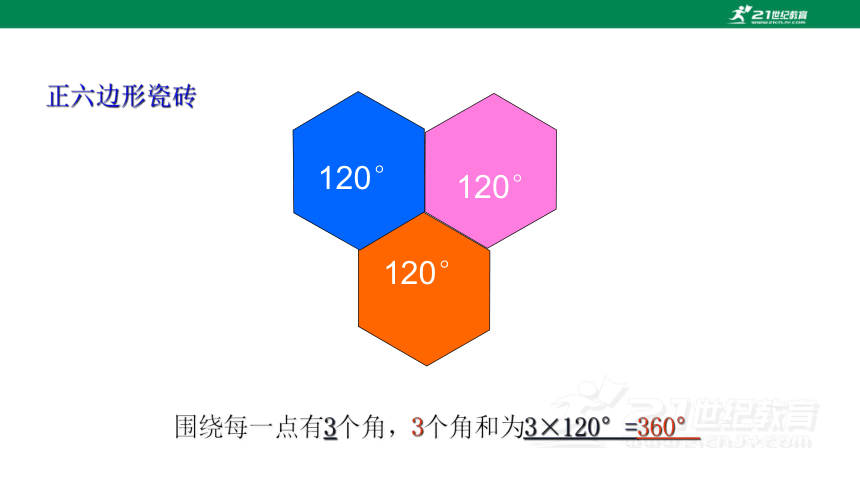
120°
120°
120°
正六边形瓷砖
围绕每一点有3个角,3个角和为3×120°=360°
正七边形正八边形呢?
想一想,为什么?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7≈128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
思考:
为什么有的正多边形能铺满地面,有的却不行呢?
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
提炼概念
能用同一种正多边形拼地板的正多边形有正三角形、正方形、正六边形.
小结:
典例精讲
例:如图所示的地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无隙的地面?
(2)像这样铺设地面,能否全用正十边形的材料?为什么?
解:(1)每个顶点周围有6个正三角形的内角,恰好可以组成一个周角.
(2)不能.
理由:因为正十边形的任意几个内角都不能组成一个周角,所以不能全用正十边形的材料.
归纳概念
用平面图形把一个平面既无______又不_________全部覆盖.
重叠
能铺满地面的多边形,围绕同一点的内角和为360°.
镶嵌
1.镶嵌定义:
2.(一般)镶嵌满足的条件:
3.正多边形镶嵌满足的条件:
正多边形的一个内角能整除360°.
缝隙
(1)能,因为四边形四个内角和为3600,将四边形四个内角
绕一点可围成一个周角.
(2)能,因为三角形三个内角的和为180°(将三角形三
个不同的内角绕一点可围成一个平角),六个内角
的和为3600 (六个内角 可围成一个周角).
(一般)镶嵌
任意一种三角形,任意一种四边形都能镶嵌.
课堂练习
1、 下列正多边形地砖中,用同一种正多边形地砖不能铺满地面的是( )
A. 正三角形 B. 正四边形 C. 正六边形 D. 正八边形
D
2、我们知道正五边形不能进行平面镶嵌,若将三个完全相同的正五边形按如图所示的方式拼接在一起,那么图中∠1的度数是( )
A. 18° B. 30° C. 36° D. 54°
C
3、 用一种正多边形能进行平面铺设的条件是( )
A. 内角都是整数度数
B. 边数是 3 的整数倍
C. 内角整除 180°
D. 内角整除 360°
D
4、已知一个正多边形的内角的度数比与其相邻的外角的度数大140°.
(1)求这个正多边形的内角与外角的度数
(2)直接写出这个正多边形的边数
(3)只用这个正多边形若干个,能否镶嵌并说明理由.
解:(1)正多边形的内角的度数为160°,外角的度数为20°
(2)18
(3)不能.
理由: ∵正多边形的内角为160°,不能整除360°,
∴不能镶嵌.
5、铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
课堂总结
用相同的正多边形铺设地面
围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
9.3.1用相同的正多边形铺设地面
华师大版 七年级 下册
教学目标
教学目标:1.通过用相同的正多边形拼地板的活动,巩固多边形的内角和
与外角和公式.
2.通过“拼地板”和相关计算,使学生从中发现能拼成一个不
留空隙,又不重叠的平面图形的关键是几个多边形的内角
和相加要等于360°.
教学重点:通过用相同的正多边形拼地板活动,巩固多边形的内角和与外角和公式.教学难点:探索用各种正多边形拼地板的过程和原理.
新知导入
情境引入
图片欣赏
思考:
用同一种正多边形铺地板,哪些能密铺不留空隙呢
铺地板的学问
新知讲解
合作学习
新课探索
围绕某一顶点铺满地面
既不留下一丝空白,又不相互重叠这叫做“平面镶嵌”“密铺”或者“满铺”.
用同一种正多边形铺地板,哪些能密铺不留空隙呢
探索
这显然与正多边形的内角大小有关.
这显然与正多边形的内角大小有关.为了探索哪些正多边形能铺满地面,请根据下图 ,完成下表.
正多边形的边数 3 4 5 6 7 … n
正多边形的内角和 180° 360° …
每个内角的度数 60° 90° …
108°
720°
540°
1080°
(n-2) · 180°
120°
135°
60°
60°
60°
60°
60°
60°
正三角形瓷砖
围绕每一点有6个角,6个角和为6×60°= 360°
90°
90°
90°
90°
正方形瓷砖
围绕每一点有4个角,4个角和为4×90°=360°
108°
108°
108°
正五边形瓷砖
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
120°
120°
120°
正六边形瓷砖
围绕每一点有3个角,3个角和为3×120°=360°
正七边形正八边形呢?
想一想,为什么?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7≈128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
思考:
为什么有的正多边形能铺满地面,有的却不行呢?
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
提炼概念
能用同一种正多边形拼地板的正多边形有正三角形、正方形、正六边形.
小结:
典例精讲
例:如图所示的地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无隙的地面?
(2)像这样铺设地面,能否全用正十边形的材料?为什么?
解:(1)每个顶点周围有6个正三角形的内角,恰好可以组成一个周角.
(2)不能.
理由:因为正十边形的任意几个内角都不能组成一个周角,所以不能全用正十边形的材料.
归纳概念
用平面图形把一个平面既无______又不_________全部覆盖.
重叠
能铺满地面的多边形,围绕同一点的内角和为360°.
镶嵌
1.镶嵌定义:
2.(一般)镶嵌满足的条件:
3.正多边形镶嵌满足的条件:
正多边形的一个内角能整除360°.
缝隙
(1)能,因为四边形四个内角和为3600,将四边形四个内角
绕一点可围成一个周角.
(2)能,因为三角形三个内角的和为180°(将三角形三
个不同的内角绕一点可围成一个平角),六个内角
的和为3600 (六个内角 可围成一个周角).
(一般)镶嵌
任意一种三角形,任意一种四边形都能镶嵌.
课堂练习
1、 下列正多边形地砖中,用同一种正多边形地砖不能铺满地面的是( )
A. 正三角形 B. 正四边形 C. 正六边形 D. 正八边形
D
2、我们知道正五边形不能进行平面镶嵌,若将三个完全相同的正五边形按如图所示的方式拼接在一起,那么图中∠1的度数是( )
A. 18° B. 30° C. 36° D. 54°
C
3、 用一种正多边形能进行平面铺设的条件是( )
A. 内角都是整数度数
B. 边数是 3 的整数倍
C. 内角整除 180°
D. 内角整除 360°
D
4、已知一个正多边形的内角的度数比与其相邻的外角的度数大140°.
(1)求这个正多边形的内角与外角的度数
(2)直接写出这个正多边形的边数
(3)只用这个正多边形若干个,能否镶嵌并说明理由.
解:(1)正多边形的内角的度数为160°,外角的度数为20°
(2)18
(3)不能.
理由: ∵正多边形的内角为160°,不能整除360°,
∴不能镶嵌.
5、铺设一间长 6 m、宽 3.5 m 的客厅地面需要同样规格的正方形地板砖,现有“40 cm×40 cm”“30 cm×30 cm”“50 cm×50 cm”和“60 cm×60 cm”的地板砖,请你设计一下,要想全部铺满,不锯破且不留一点空隙,选哪一种规格?为什么?需要多少块?
解:选“50 cm×50 cm”规格的.
理由:∵6 m =600c m,3.5 m = 350 cm,
600,350 都是 50 的倍数,
∴选“50 cm×5 0cm”规格的.
需要 7×12 = 84(块).
课堂总结
用相同的正多边形铺设地面
围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
