数学人教A版(2019)必修第二册8.5.3平面与平面平行 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.5.3平面与平面平行 课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 526.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 06:39:56 | ||
图片预览






文档简介
(共15张PPT)
8.5.3 平面与平面平行
人教A版2019高中数学必修第二册
8.5 空间直线、平面的平行
学习目标
1.理解并掌握平面与平面平行的判定定理,明确定理中“相交”两字的重要性.
2.理解并能证明平面与平面平行的性质定理.
3.能利用平面与平面平行的判定定理和性质定理解决有关平行的问题
(1)平行
(2)相交
1.平面与平面有几种位置关系?分别是什么?
2.平面与平面平行的定义?
定义:如果两个平面没有公共点就称这两个平面平行
如何判定平面与平面平行?
复习回顾
【情境导入】
上海世界博览会的中国国家馆被永久保留.中国国家馆表达了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化的精神与气质,展馆共分三层.
【问题1】展馆的每两层所在的平面什么关系?【问题2】上层面上任一直线状物体与下层地面有何位置关系?【问题3】上下两层所在的平面与侧墙所在平面分别相交,它们的交线是什么位置关系?
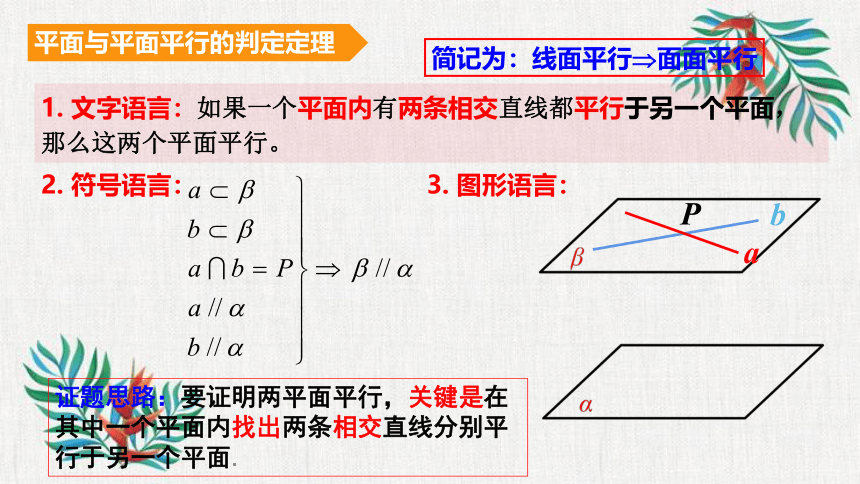
1. 文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
2. 符号语言:
3. 图形语言:
a
b
P
证题思路:要证明两平面平行,关键是在其中一个平面内找出两条相交直线分别平行于另一个平面.
平面与平面平行的判定定理
简记为:线面平行 面面平行
例题1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
探究一、平面与平面平行的判定
【变式】如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
如图,由棱柱的性质知,B1C1∥BC,B1C1=BC.又D、E分别为BC,B1C1的中点,所以C1E∥DB,C1E=DB,则四边形C1DBE为平行四边形,因此EB∥C1D.又C1D 平面ADC1,EB 平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1∥BD,EB1=BD,所以四边形EDBB1为平行四边形,则ED∥B1B,ED=B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED∥A1A,ED=A1A,则四边形EDAA1为平行四边形,所以A1E∥AD.又A1E 平面ADC1,AD 平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1,A1E 平面A1EB,EB 平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.
【归纳总结】证明面面平行的方法
(1)定义法:两个平面没有公共点;
(2)判定定理:一个平面内的两条相交直线分别平行于另一个平面;
(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β;
(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.
【练习】
如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,点M,N,Q分别在PA,BD,PD上,且PM︰MA=BN︰ND=PQ︰QD,求证:平面MNQ∥平面PBC.
[解析] ∵在三角形PBD中,BN︰ND=PQ︰QD,∴QN∥PB,∴QN∥平面PBC,同理PM︰MA=PQ︰QD,∴MQ∥AD.又底面ABCD是平行四边形,则AD∥BC,∴MQ∥BC,∴MQ∥平面PBC.而MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,∴平面MNQ∥平面PBC.
1. 文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
2. 符号语言:
3. 图形语言:
平面与平面平行的性质定理
简述为:面面平行 线线平行
例题2 求证:夹在两个平行平面间的平行线段相等.
已知:如图,α∥β,AB∥CD,A∈α,C∈α,B∈β,D∈β,
求证:AB=CD
夹在两个平行平面间的所有平行线段相等.
探究二、平面与平面平行的性质
【变式】如图,两条异面直线AB,CD与三个平行平面α,β,γ分别相交于A,E,B及C,F,D,又AD,BC与平面β的交点为H,G.求证:四边形EHFG为平行四边形.
【归纳总结】利用平面与平面平行的性质定理解题的步骤
【练习】
如图所示,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.
[证明] 因为D,E分别是PA,PB的中点,所以DE∥AB.又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC.同理DF∥平面ABC,且DE∩DF=D,所以平面DEF∥平面ABC.又平面PCM∩平面DEF=NF,平面PCM∩平面ABC=CM,所以NF∥CM.
面面平行
判定
性质
线线平行
线面平行
判定
性质
性质
1.知识内容
转化
空间
平面
无限
有限
面面平行
线面平行
线线平行
2.数学思想
课堂小结
8.5.3 平面与平面平行
人教A版2019高中数学必修第二册
8.5 空间直线、平面的平行
学习目标
1.理解并掌握平面与平面平行的判定定理,明确定理中“相交”两字的重要性.
2.理解并能证明平面与平面平行的性质定理.
3.能利用平面与平面平行的判定定理和性质定理解决有关平行的问题
(1)平行
(2)相交
1.平面与平面有几种位置关系?分别是什么?
2.平面与平面平行的定义?
定义:如果两个平面没有公共点就称这两个平面平行
如何判定平面与平面平行?
复习回顾
【情境导入】
上海世界博览会的中国国家馆被永久保留.中国国家馆表达了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化的精神与气质,展馆共分三层.
【问题1】展馆的每两层所在的平面什么关系?【问题2】上层面上任一直线状物体与下层地面有何位置关系?【问题3】上下两层所在的平面与侧墙所在平面分别相交,它们的交线是什么位置关系?
1. 文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
2. 符号语言:
3. 图形语言:
a
b
P
证题思路:要证明两平面平行,关键是在其中一个平面内找出两条相交直线分别平行于另一个平面.
平面与平面平行的判定定理
简记为:线面平行 面面平行
例题1 如图,已知正方体ABCD-A1B1C1D1.
求证:平面AB1D1//平面BC1D.
探究一、平面与平面平行的判定
【变式】如图所示,在三棱柱ABC-A1B1C1中,点D,E分别是BC与B1C1的中点.求证:平面A1EB∥平面ADC1.
如图,由棱柱的性质知,B1C1∥BC,B1C1=BC.又D、E分别为BC,B1C1的中点,所以C1E∥DB,C1E=DB,则四边形C1DBE为平行四边形,因此EB∥C1D.又C1D 平面ADC1,EB 平面ADC1,所以EB∥平面ADC1.连接DE,同理,EB1∥BD,EB1=BD,所以四边形EDBB1为平行四边形,则ED∥B1B,ED=B1B.因为B1B∥A1A,B1B=A1A(棱柱的性质),所以ED∥A1A,ED=A1A,则四边形EDAA1为平行四边形,所以A1E∥AD.又A1E 平面ADC1,AD 平面ADC1,所以A1E∥平面ADC1.由A1E∥平面ADC1,EB∥平面ADC1,A1E 平面A1EB,EB 平面A1EB,且A1E∩EB=E,所以平面A1EB∥平面ADC1.
【归纳总结】证明面面平行的方法
(1)定义法:两个平面没有公共点;
(2)判定定理:一个平面内的两条相交直线分别平行于另一个平面;
(3)转化为线线平行:平面α内的两条相交直线与平面β内的两条相交直线分别平行,则α∥β;
(4)利用平行平面的传递性:若α∥β,β∥γ,则α∥γ.
【练习】
如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,点M,N,Q分别在PA,BD,PD上,且PM︰MA=BN︰ND=PQ︰QD,求证:平面MNQ∥平面PBC.
[解析] ∵在三角形PBD中,BN︰ND=PQ︰QD,∴QN∥PB,∴QN∥平面PBC,同理PM︰MA=PQ︰QD,∴MQ∥AD.又底面ABCD是平行四边形,则AD∥BC,∴MQ∥BC,∴MQ∥平面PBC.而MQ∩NQ=Q,MQ 平面MNQ,NQ 平面MNQ,∴平面MNQ∥平面PBC.
1. 文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
2. 符号语言:
3. 图形语言:
平面与平面平行的性质定理
简述为:面面平行 线线平行
例题2 求证:夹在两个平行平面间的平行线段相等.
已知:如图,α∥β,AB∥CD,A∈α,C∈α,B∈β,D∈β,
求证:AB=CD
夹在两个平行平面间的所有平行线段相等.
探究二、平面与平面平行的性质
【变式】如图,两条异面直线AB,CD与三个平行平面α,β,γ分别相交于A,E,B及C,F,D,又AD,BC与平面β的交点为H,G.求证:四边形EHFG为平行四边形.
【归纳总结】利用平面与平面平行的性质定理解题的步骤
【练习】
如图所示,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.
[证明] 因为D,E分别是PA,PB的中点,所以DE∥AB.又DE 平面ABC,AB 平面ABC,所以DE∥平面ABC.同理DF∥平面ABC,且DE∩DF=D,所以平面DEF∥平面ABC.又平面PCM∩平面DEF=NF,平面PCM∩平面ABC=CM,所以NF∥CM.
面面平行
判定
性质
线线平行
线面平行
判定
性质
性质
1.知识内容
转化
空间
平面
无限
有限
面面平行
线面平行
线线平行
2.数学思想
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
