物理人教版(2019)必修第二册8.2重力势能(共25张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.2重力势能(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 831.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-22 10:04:14 | ||
图片预览







文档简介
(共25张PPT)
重力势能
新课导入
雪崩
2002年9月21日上午,俄罗斯高加索北奥塞梯地区的一个村庄发生雪崩,造成至少100人失踪。
陨石坑
美国内华达州亚利桑那
美国内华达州亚利桑那陨石坑。这个陨石坑是5万年前,一颗直径约为30~50米的铁质流星撞击地面的结果。这颗流星重约50万千克、速度达到20千米/秒,爆炸力相当于2000万千克梯恩梯(TNT),超过美国轰炸日本广岛那颗原子弹的一千倍。爆炸在地面上产生了一个直径约1245米,平均深度达180米的大坑。据说,坑中可以安放下20个足球场,四周的看台则能容纳200多万观众。
几个概念
力:物体之间的相互作用。
重力:物体由于地球的吸引而受到的力
势能:相互作用的物体凭借其位置而具有的
能量。
一个新的概念——重力势能
重力势能:
物体由于被举高而具有的能叫做重力势能。
物体的高度发生变化时,重力要做功:物体被举
高时,重力做负功;物体下降时,重力做正功。
因此,认识这种势能,不能脱离对重力做功的研究。
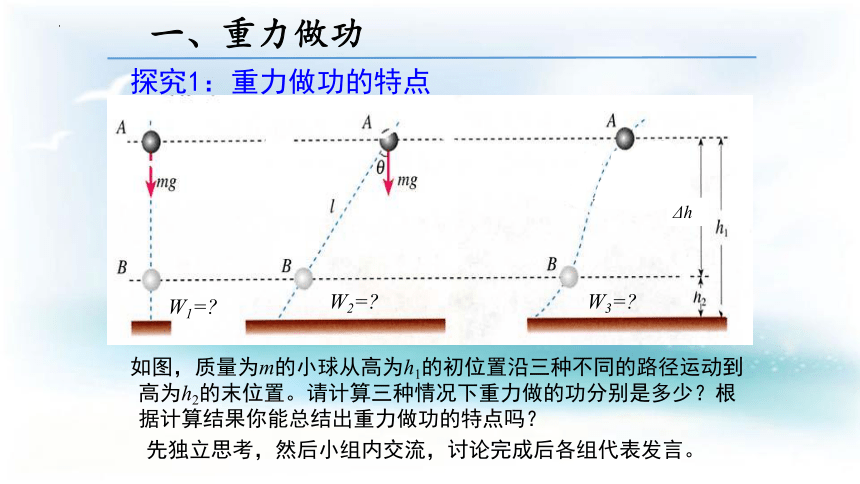
一、重力做功
Δh
如图,质量为m的小球从高为h1的初位置沿三种不同的路径运动到高为h2的末位置。请计算三种情况下重力做的功分别是多少?根据计算结果你能总结出重力做功的特点吗?
先独立思考,然后小组内交流,讨论完成后各组代表发言。
W1=
W2=
W3=
探究1:重力做功的特点
一、重力做功
类型3
类型2
类型1
B
B
Δh1
Δh2
Δh3
h
h1
h2
A
mg
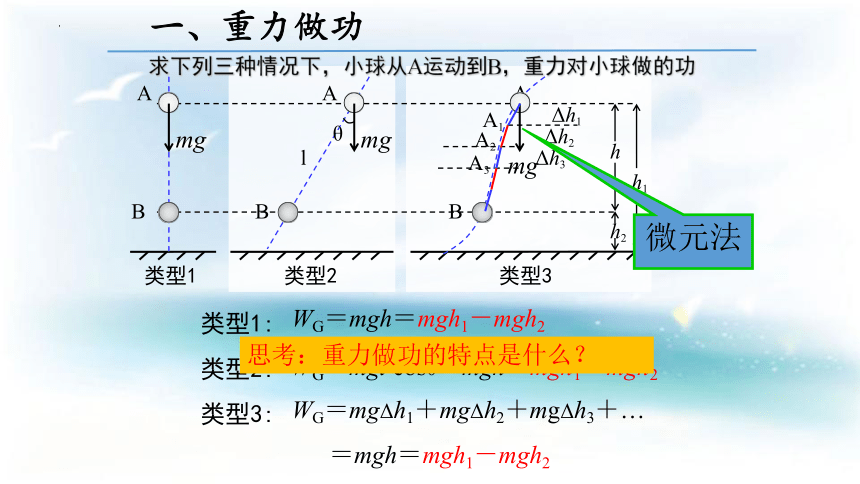
类型1:
类型2:
类型3:
A1
A2
A3
WG=mgh=mgh1-mgh2
WG=mgl cosθ=mgh=mgh1-mgh2
WG=mgΔh1+mgΔh2+mgΔh3+…
=mgh=mgh1-mgh2
l
B
θ
mg
A
A
mg
求下列三种情况下,小球从A运动到B,重力对小球做的功
微元法
思考:重力做功的特点是什么?
可见物体在从A运动到B的过程中无论是直线还是曲线重力做功:
只跟它的起点和终点的位置(高度差)有关,与物体运动的路径无关。
即:WG = mgΔh
可见,重力做的功等于“mgh”这个量的变化,在物理学中, “mgh”是一个由特殊意义的物理量,就用这个物理量表示物体的重力势能。
二、重力势能
1、定义:物体由于被举高而具有的能叫做重力势能。标量,状态量。
2、重力势能的表达式: Ep = mgh
m — 物体的质量,单位:千克(kg)
g — 重力加速度,单位:米/秒2(m/s2)
h —物体的高度,单位:米(m)
Ep — 物体的重力势能,单位:焦(J)
即:物体的重力势能等于物体的重量和它的高度的乘积.
三、重力做功与重力势能的变化关系
WG = Ep1 - Ep2
重力做功WG (正、负) 重力势能EP (增加、减少) 重力做功和重力势能变化的关系
物体 上升
物体 下降
物体克服重力做的功等于重力势能的增加
重力做的功等于重力势能的减少
负功
正功
增加
减少
四、重力势能的相对性
因为高度是一个相对量,所以重力势能也是一个相对量,因此,重力势能具有相对性。要确定物体在某位置处的重力势能,必须选定一个参考平面——零势能面。
在零势能面上方的物体的高度是正值,重力势能也是正值;
在零势能面下方的物体的高度是负值,重力势能也是负值。
势能是状态量、标量。+、–表示大小,不代表方向。
参考平面的选取是任意的,选取哪个平面做参考平面,可视问题的方便而定,通常选地面为参考面。
五、重力势能的系统性
重力势能属于物体和地球组成的系统 。
必须指出的是,重力势能跟重力做功密切相关,而重力是地球与物体之间的相互作用力。也就是说,倘若没有地球,就谈不上重力。所以,严格说来,重力势能是地球与物体所组成的这个物体“系统”所共有的,而不是地球上的物体单独具有的。
平常所说的“物体”的重力势能,只是一种习惯简化的说法。
参考平面 小球在A点重力势能 小球在B点重力势能 下落过程小球重力做功 下落过程小球重力势能变化量
桌面
地面
6J
10J
-4J
0
10J
10J
-10J
-10J
h1
h2
A
B
WG和△EP与参考平面的选择无关。
△Ep的绝对性
民法典:第一千二百五十四条规定:禁止从建筑物中抛掷物品。
例1: 如图,质量0.5kg的小球,从桌面以上h1=1.2m的A点落到地面的B点,桌面高h2=0.8m.请按要求填写下表。(g=9.8m/s2)
h1
h2
A
B
参考 平面 小球在A点重力势能 小球在B点重力势能 下落过程小球重力做功 下落过程小球重力势能变化
桌面
地面
选取不同的参考平面,物体的重力势能的数值不同
对一个确定的过程,WG和△EP与参考面的选择无关
5.88J
-3.92J
9.8J
9.8J
9.8J
0
9.8J
9.8J
例2:质量为 0. 5 kg 的钢球,在离地面10 m 高处自由下落 1 s 后,它的重力势能减少了多少?当它自由下落到地面时,钢球获得的动能多大?
解:以地面为零势能面,E0 = 0 。钢球自由下落 1 s ,下落的高度为
根据重力做功和重力势能之间的关系,可知重力势能减少量为
根据动能定理 ,钢球自由下落到地面时获得的动能为
弹性势能
这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。
弹性势能
1.概念:
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
2.对弹性势能的理解:
(1)系统性:弹性势能是发生弹性形变的物体上所有质点因相对位置改变和发生弹力作用而具有的能量,因此弹性势能具有系统性。
(2)相对性:弹性势能的大小与选定的零势能位置有关,对于弹簧,一般规定弹簧处于原长为其零势能的位置。
弹性势能
4. 弹性势能与弹力做功的关系
(1)弹力做正功时,弹性势能减小。
(2)弹力做负功时,弹性势能增大。
(3)弹力做功与弹性势能变化的关系为W弹 = -△EP。
3. 弹性势能跟弹性形变的大小有关,还跟弹簧的劲度系数有关。
巩固训练
(多选)关于弹性势能,下列说法中正确的是( )
A. 任何发生弹性形变的物体,都具有弹性势能
B. 任何具有弹性势能的物体,一定发生了弹性形变
C. 物体只要发生形变,就一定具有弹性势能
D. 弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关
AB
课堂小结
一、重力做的功
1.表达式:
2.只跟它的 有关,而跟物体运动的 无关。
1.表达式:
2.国际单位:
焦耳,简称焦,符号是J
3.重力做的功与重力势能的关系:
二、重力势能
起点和终点的位置
路径
课堂小结
三、重力势能的相对性
1.参考平面
2.重力势能的相对性
3.重力势能的绝对性
4.重力势能的系统性
1.概念:
四、弹性势能
2.弹性势能跟 有关,还跟弹簧的 有关。
3.弹力做功与弹性势能变化的关系为 。
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
弹性形变的大小
劲度系数
W弹 = -△EP
1、选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能改变量( )
A、都具有不同的数值
B、都具有相同的数值
C、前者具有相同的数值,后者具有不同的数值
D、前者具有不同的数值,后者具有相同的数值
练习:
D
2、起重机以5m/s2的加速度将质量为1t的物体匀减速地沿竖直方向提升高度10m,则起重机钢索的拉力对物体做的功为多少?物体克服重力做功为多少?物体的重力势能变化了多少?
3、一个质量为50kg的女孩从山脚到山顶走了60m 之后,她的重力势能增加了9800J,求山的高度。
重力势能
新课导入
雪崩
2002年9月21日上午,俄罗斯高加索北奥塞梯地区的一个村庄发生雪崩,造成至少100人失踪。
陨石坑
美国内华达州亚利桑那
美国内华达州亚利桑那陨石坑。这个陨石坑是5万年前,一颗直径约为30~50米的铁质流星撞击地面的结果。这颗流星重约50万千克、速度达到20千米/秒,爆炸力相当于2000万千克梯恩梯(TNT),超过美国轰炸日本广岛那颗原子弹的一千倍。爆炸在地面上产生了一个直径约1245米,平均深度达180米的大坑。据说,坑中可以安放下20个足球场,四周的看台则能容纳200多万观众。
几个概念
力:物体之间的相互作用。
重力:物体由于地球的吸引而受到的力
势能:相互作用的物体凭借其位置而具有的
能量。
一个新的概念——重力势能
重力势能:
物体由于被举高而具有的能叫做重力势能。
物体的高度发生变化时,重力要做功:物体被举
高时,重力做负功;物体下降时,重力做正功。
因此,认识这种势能,不能脱离对重力做功的研究。
一、重力做功
Δh
如图,质量为m的小球从高为h1的初位置沿三种不同的路径运动到高为h2的末位置。请计算三种情况下重力做的功分别是多少?根据计算结果你能总结出重力做功的特点吗?
先独立思考,然后小组内交流,讨论完成后各组代表发言。
W1=
W2=
W3=
探究1:重力做功的特点
一、重力做功
类型3
类型2
类型1
B
B
Δh1
Δh2
Δh3
h
h1
h2
A
mg
类型1:
类型2:
类型3:
A1
A2
A3
WG=mgh=mgh1-mgh2
WG=mgl cosθ=mgh=mgh1-mgh2
WG=mgΔh1+mgΔh2+mgΔh3+…
=mgh=mgh1-mgh2
l
B
θ
mg
A
A
mg
求下列三种情况下,小球从A运动到B,重力对小球做的功
微元法
思考:重力做功的特点是什么?
可见物体在从A运动到B的过程中无论是直线还是曲线重力做功:
只跟它的起点和终点的位置(高度差)有关,与物体运动的路径无关。
即:WG = mgΔh
可见,重力做的功等于“mgh”这个量的变化,在物理学中, “mgh”是一个由特殊意义的物理量,就用这个物理量表示物体的重力势能。
二、重力势能
1、定义:物体由于被举高而具有的能叫做重力势能。标量,状态量。
2、重力势能的表达式: Ep = mgh
m — 物体的质量,单位:千克(kg)
g — 重力加速度,单位:米/秒2(m/s2)
h —物体的高度,单位:米(m)
Ep — 物体的重力势能,单位:焦(J)
即:物体的重力势能等于物体的重量和它的高度的乘积.
三、重力做功与重力势能的变化关系
WG = Ep1 - Ep2
重力做功WG (正、负) 重力势能EP (增加、减少) 重力做功和重力势能变化的关系
物体 上升
物体 下降
物体克服重力做的功等于重力势能的增加
重力做的功等于重力势能的减少
负功
正功
增加
减少
四、重力势能的相对性
因为高度是一个相对量,所以重力势能也是一个相对量,因此,重力势能具有相对性。要确定物体在某位置处的重力势能,必须选定一个参考平面——零势能面。
在零势能面上方的物体的高度是正值,重力势能也是正值;
在零势能面下方的物体的高度是负值,重力势能也是负值。
势能是状态量、标量。+、–表示大小,不代表方向。
参考平面的选取是任意的,选取哪个平面做参考平面,可视问题的方便而定,通常选地面为参考面。
五、重力势能的系统性
重力势能属于物体和地球组成的系统 。
必须指出的是,重力势能跟重力做功密切相关,而重力是地球与物体之间的相互作用力。也就是说,倘若没有地球,就谈不上重力。所以,严格说来,重力势能是地球与物体所组成的这个物体“系统”所共有的,而不是地球上的物体单独具有的。
平常所说的“物体”的重力势能,只是一种习惯简化的说法。
参考平面 小球在A点重力势能 小球在B点重力势能 下落过程小球重力做功 下落过程小球重力势能变化量
桌面
地面
6J
10J
-4J
0
10J
10J
-10J
-10J
h1
h2
A
B
WG和△EP与参考平面的选择无关。
△Ep的绝对性
民法典:第一千二百五十四条规定:禁止从建筑物中抛掷物品。
例1: 如图,质量0.5kg的小球,从桌面以上h1=1.2m的A点落到地面的B点,桌面高h2=0.8m.请按要求填写下表。(g=9.8m/s2)
h1
h2
A
B
参考 平面 小球在A点重力势能 小球在B点重力势能 下落过程小球重力做功 下落过程小球重力势能变化
桌面
地面
选取不同的参考平面,物体的重力势能的数值不同
对一个确定的过程,WG和△EP与参考面的选择无关
5.88J
-3.92J
9.8J
9.8J
9.8J
0
9.8J
9.8J
例2:质量为 0. 5 kg 的钢球,在离地面10 m 高处自由下落 1 s 后,它的重力势能减少了多少?当它自由下落到地面时,钢球获得的动能多大?
解:以地面为零势能面,E0 = 0 。钢球自由下落 1 s ,下落的高度为
根据重力做功和重力势能之间的关系,可知重力势能减少量为
根据动能定理 ,钢球自由下落到地面时获得的动能为
弹性势能
这些物体都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。
弹性势能
1.概念:
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
2.对弹性势能的理解:
(1)系统性:弹性势能是发生弹性形变的物体上所有质点因相对位置改变和发生弹力作用而具有的能量,因此弹性势能具有系统性。
(2)相对性:弹性势能的大小与选定的零势能位置有关,对于弹簧,一般规定弹簧处于原长为其零势能的位置。
弹性势能
4. 弹性势能与弹力做功的关系
(1)弹力做正功时,弹性势能减小。
(2)弹力做负功时,弹性势能增大。
(3)弹力做功与弹性势能变化的关系为W弹 = -△EP。
3. 弹性势能跟弹性形变的大小有关,还跟弹簧的劲度系数有关。
巩固训练
(多选)关于弹性势能,下列说法中正确的是( )
A. 任何发生弹性形变的物体,都具有弹性势能
B. 任何具有弹性势能的物体,一定发生了弹性形变
C. 物体只要发生形变,就一定具有弹性势能
D. 弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关
AB
课堂小结
一、重力做的功
1.表达式:
2.只跟它的 有关,而跟物体运动的 无关。
1.表达式:
2.国际单位:
焦耳,简称焦,符号是J
3.重力做的功与重力势能的关系:
二、重力势能
起点和终点的位置
路径
课堂小结
三、重力势能的相对性
1.参考平面
2.重力势能的相对性
3.重力势能的绝对性
4.重力势能的系统性
1.概念:
四、弹性势能
2.弹性势能跟 有关,还跟弹簧的 有关。
3.弹力做功与弹性势能变化的关系为 。
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
弹性形变的大小
劲度系数
W弹 = -△EP
1、选择不同的水平面作为参考平面,物体在某一位置的重力势能和某一过程中重力势能改变量( )
A、都具有不同的数值
B、都具有相同的数值
C、前者具有相同的数值,后者具有不同的数值
D、前者具有不同的数值,后者具有相同的数值
练习:
D
2、起重机以5m/s2的加速度将质量为1t的物体匀减速地沿竖直方向提升高度10m,则起重机钢索的拉力对物体做的功为多少?物体克服重力做功为多少?物体的重力势能变化了多少?
3、一个质量为50kg的女孩从山脚到山顶走了60m 之后,她的重力势能增加了9800J,求山的高度。
