第七章:平面直角坐标系练习题(含解析)2021-2022学年山东省七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第七章:平面直角坐标系练习题(含解析)2021-2022学年山东省七年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 16:57:55 | ||
图片预览



文档简介
第七章:平面直角坐标系 练习题
一、单选题
1.(2022春·山东聊城·七年级统考期末)2021年6月17日神舟十二号飞船于在甘肃酒泉发射升空,在太空驻留90天后于9月14日返回地球,下列描述能确定飞船着陆位置的是( )
A.内蒙古中部
B.酒泉卫星发射中心东南方向处
C.东经
D.北纬
2.(2022春·山东菏泽·七年级统考期末)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )
A. B. C. D.
3.(2022春·山东临沂·七年级统考期末)在平面直角坐标系中,点B(2,3)到x轴的距离为( )
A.3 B.2 C.-3 D.-2
4.(2022春·山东滨州·七年级统考期末)已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·山东德州·七年级统考期末)下列语句正确的是( ).
A.在平面直角坐标系中,与表示两个不同的点
B.平行于轴的直线上所有点的横坐标都相同
C.若点在轴上,则
D.点到轴的距离为3
6.(2022春·山东聊城·七年级统考期末)在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
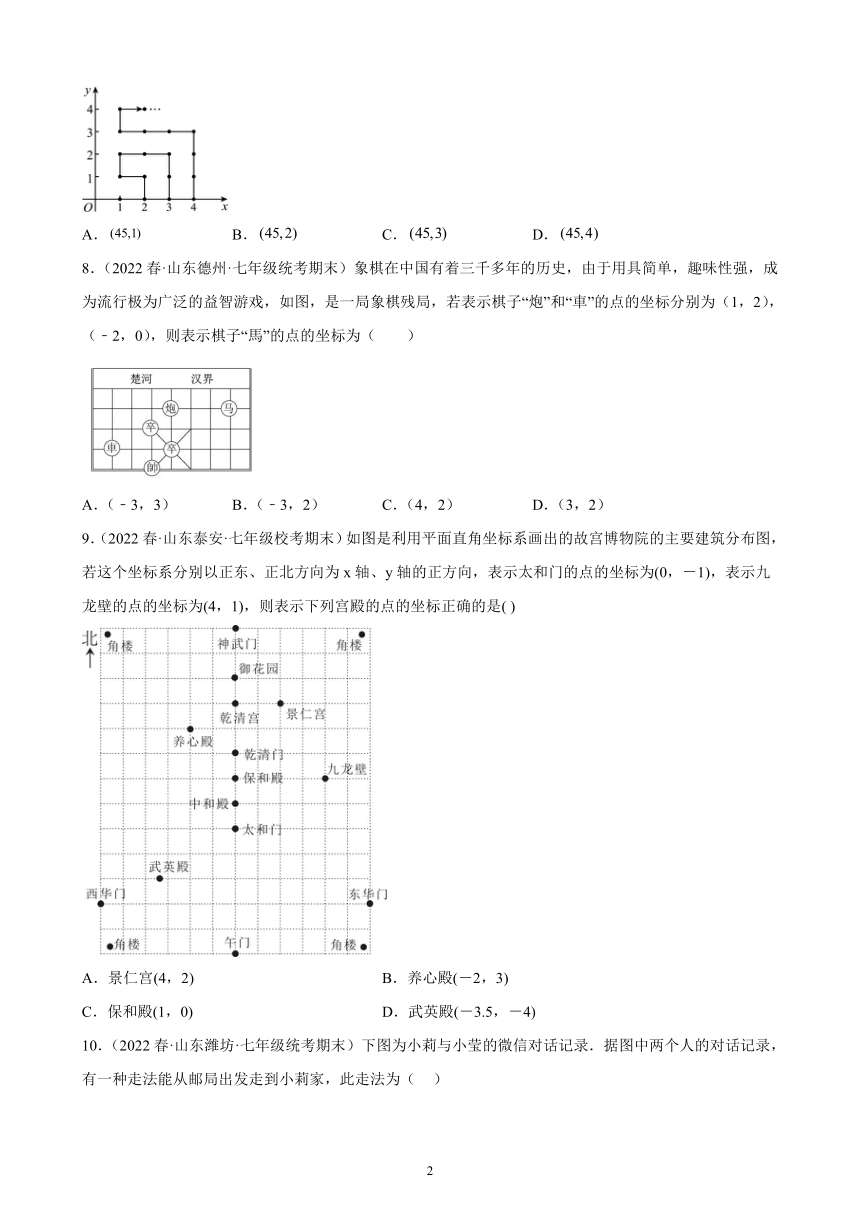
7.(2022春·山东济宁·七年级统考期末)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2022个点的坐标为( )
A. B. C. D.
8.(2022春·山东德州·七年级统考期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,是一局象棋残局,若表示棋子“炮”和“車”的点的坐标分别为(1,2),(﹣2,0),则表示棋子“馬”的点的坐标为( )
A.(﹣3,3) B.(﹣3,2) C.(4,2) D.(3,2)
9.(2022春·山东泰安·七年级校考期末)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2) B.养心殿(-2,3)
C.保和殿(1,0) D.武英殿(-3.5,-4)
10.(2022春·山东潍坊·七年级统考期末)下图为小莉与小莹的微信对话记录.据图中两个人的对话记录,有一种走法能从邮局出发走到小莉家,此走法为( )
A.向北直走400米,再向东直走300米 B.向北直走500米,再向西直走100米
C.向北直走100米,再向西直走500米 D.向北直走200米,再向东直走300米
11.(2022春·山东临沂·七年级统考期末)在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
12.(2022春·山东临沂·七年级统考期末)将某图形的各点的纵坐标减去2,横坐标加上1,可将该图形( )
A.横向向左平移2个单位,纵向向上平移2个单位
B.横向向左平移1个单位,纵向向下平移2个单位
C.横向向右平移1个单位,纵向向上平移2个单位
D.横向向右平移1个单位,纵向向下平移2个单位
13.(2022春·山东滨州·七年级统考期末)线段是由线段平移得到的,点的对应点为,则的对应点B的坐标为( ).
A. B. C. D.
二、填空题
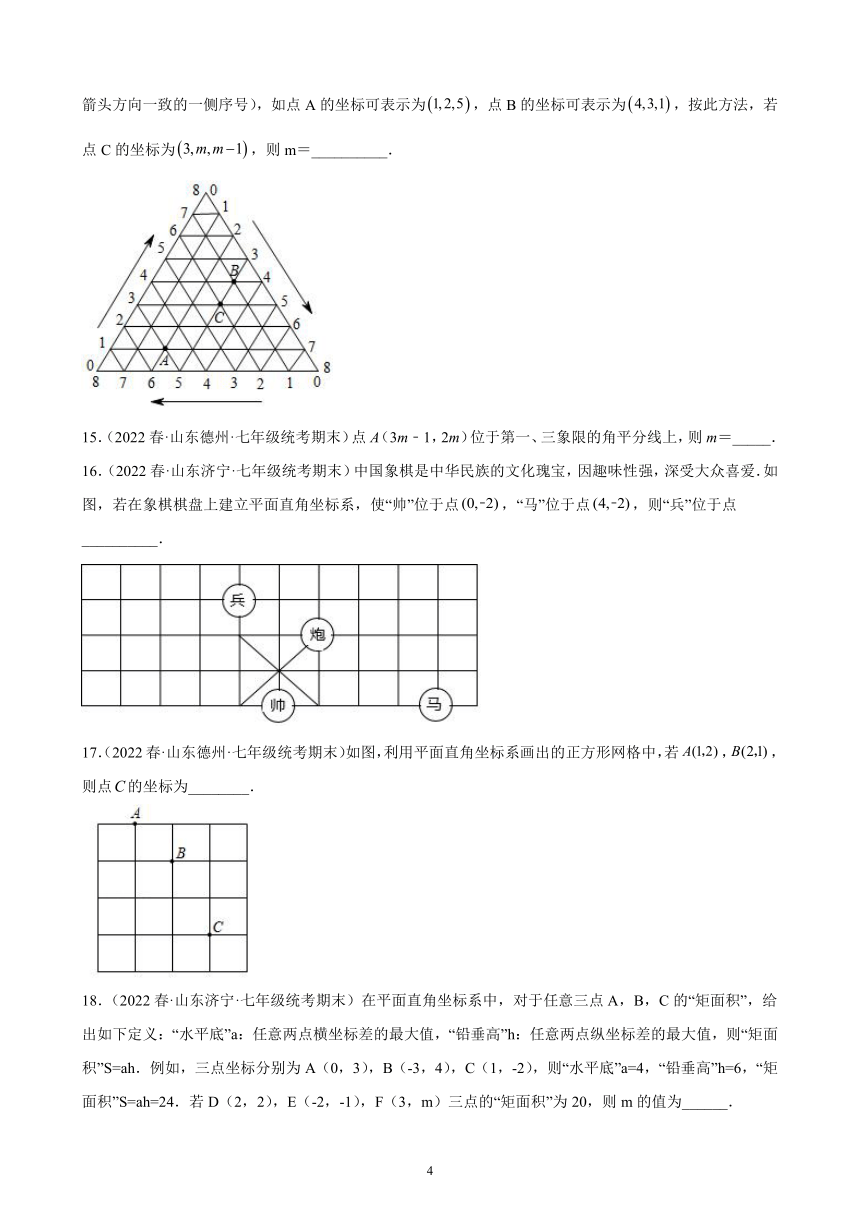
14.(2022春·山东德州·七年级统考期末)如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号),如点A的坐标可表示为,点B的坐标可表示为,按此方法,若点C的坐标为,则m=__________.
15.(2022春·山东德州·七年级统考期末)点A(3m﹣1,2m)位于第一、三象限的角平分线上,则m=_____.
16.(2022春·山东济宁·七年级统考期末)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于点__________.
17.(2022春·山东德州·七年级统考期末)如图,利用平面直角坐标系画出的正方形网格中,若,,则点的坐标为________.
18.(2022春·山东济宁·七年级统考期末)在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
19.(2022春·山东德州·七年级统考期末)如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是_____.
20.(2022春·山东聊城·七年级统考期末)如图,雷达探测器测得A,B,C三个目标,如果A,B的位置分别表示为(4,60°),(2,210°).则目标C的位置表示为______.
21.(2022春·山东济宁·七年级统考期末)如图,已知Rt△ABC的边BC在x轴上,,且A(1,2),B(-2,0)若将△ABC平移,使点B落在点A处,则点C的对应点的坐标为___________
三、解答题
22.(2022春·山东滨州·七年级统考期末)已知平面直角坐标系中有一点.
(1)若点M到x轴的距离为1,请求出点M的坐标.
(2)若点),且轴,求线段的长度.
23.(2022春·山东济宁·七年级统考期末)如图①,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由.
(3)若过作交轴于,且,分别平分,,如图②,求的度数.
24.(2022春·山东菏泽·七年级统考期末)在平面直角坐标系中,已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.
(1)点P在过A(2,-5)点,且与x轴平行的直线上;
(2)点P到两坐标轴的距离相等;
25.(2022春·山东临沂·七年级统考期末)如图,、经过某种变换得到的图形,点与点,点与点,点与点分别是对应点.
(1)分别写出点与点,点与点,点与点的坐标,并说说对应点的坐标有哪些特征;
(2)若点与点也是通过上述变换得到的对应点,求、的值.
26.(2022春·山东聊城·七年级统考期末)如图是某市火车站及周围的平面示意图,已知超市的坐标是,市场的坐标是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出体育场、火车站和文化宫的坐标;
(3)准备在处建汽车站,在处建花坛,请你标出汽车站和花坛的位置.
27.(2022春·山东济宁·七年级统考期末)在平面直角坐标系中,的三个顶点坐标分别是.
(1)画出;
(2)将平移,使点A平移到原点O,画出平移后的图形并写出点B和点C的对应点坐标.
28.(2022春·山东德州·七年级统考期末)在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)在平面直角坐标系中画出;
(2)平移,使点A与点重合,写出点、点平移后的所得点的坐标,并描述这个平移过程.
(3)求的面积
29.(2022春·山东滨州·七年级统考期末)如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
参考答案:
1.B
【分析】根据坐标确定位置需要两个数据解答.
【详解】解:酒泉卫星发射中心东南方向1000km处能确定位置.
故选:B.
【点睛】本题考查了确定位置,理解确定位置需要两个数据是解题的关键.
2.D
【分析】根据点到坐标轴的距离及点所在的象限解答即可.
【详解】解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:D.
【点睛】此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
3.A
【分析】根据点的纵坐标的绝对值是点到x轴的距离即可得答案.
【详解】解:在平面直角坐标系中,点(2,3)到x轴的距离为3.
故选:A.
【点睛】本题考查了点的坐标,熟练掌握点的纵坐标的绝对值是点到x轴的距离是解题的关键.
4.C
【分析】根据直线ABx轴可得点A、B的纵坐标相等可求出a的值,根据点P在x轴的负半轴上,得到b<0,然后判断点M的横坐标与纵坐标的正负即可解答.
【详解】解:∵直线ABx轴,
∴2a+2=4,解得:a=1,
∵点P在x轴的负半轴上,
∴b<0,
∴b-a=b-1<0,a-2=1-2=-1<0,
.点M在第三象限.
故选:C.
【点睛】本题主要考查了坐标与图形性质,根据直线ABx轴可得点A,B的纵坐标相等是解答本题的关键.
5.A
【分析】根据平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点逐一判断即可得.
【详解】A.在平面直角坐标系中, ( 3,5) 与 (5, 3) 表示两个不同的点,此选项正确,符合题意;
B.平行于 x 轴的直线上所有点的纵坐标都相同,此选项错误,不符合题意;
C.若点 P(a,b) 在 y 轴上,则a=0 ,此选项错误,不符合题意;
D.点 P( 3,4) 到 x 轴的距离为4,此选项错误,不符合题意;
故选:A.
【点睛】本题主要考查坐标与图形的性质,解题的关键是掌握平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点.
6.D
【分析】分类讨论:当C点在y轴上,设C(0,t),根据三角形面积公式得到 |t﹣3| 2=6,当C点在x轴上,设C(m,0),根据三角形面积公式得到|m+2| 3=6,然后分别解绝对值方程求出t和m即可得到C点坐标.
【详解】解:分两种情况:
①当C点在y轴上,设C(0,t),
∵三角形ABC的面积为6,
∴ |t﹣3| 2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9),
②当C点在x轴上,设C(m,0),
∵三角形ABC的面积为6,
∴ |m+2| 3=6,
解得m=2或﹣6.
∴C点坐标为(2,0),(﹣6,0),
综上所述,C点有4个.
故选:D.
【点睛】此题重点考查学生对平面直角坐标系上的点的应用,掌握平面直角坐标系的点的性质是解题的关键.
7.C
【分析】以正方形最外边上的点为准考虑,点的总个数等于最右下角的点横坐标n的平方,且横坐标n为奇数时最后一个点在x轴上,n为偶数时,最后一个点坐标为(1,n-1),求出与2022最接近的平方数为2025,然后根据上述规律写出第2022个点的坐标即可.
【详解】解:由图形可知,图中各点分别组成了正方形点阵,每个正方形点阵的整点数量依次为最右下角点横坐标的平方,且当正方形最右下角点的横坐标为奇数时,这个点可以看做按照运动方向到达x轴,当正方形最右下角点的横坐标为偶数时,这个点可以看作按照运动方向离开x轴,
∵452=2025,
∴第2025个点在x轴上坐标为(45,0),
则第2022个点坐标为(45,3),
故答案为:C.
【点睛】本题考查了点的坐标,观察出点的个数与横坐标存在平方关系是解题的关键,解答时除了注意点坐标的变化外,还要注意点的运动方向.
8.C
【分析】根据棋子“炮”和“車”的点坐标,推断出原点位置,进而可得出“馬”的点的坐标.
【详解】解:如图所示,根据“車”的点坐标为,可知轴在“車”所在的横线上,
又根据“炮”的点坐标,可推出原点坐标如图所示,
进而可知“馬”的点的坐标为.
故选:C.
【点睛】本题综合考查点的坐标位置的确定.解答本题的关键是由“炮”和“車”的点坐标确定出原点的坐标.
9.B
【详解】试题分析:本题考查了点的坐标问题,解题关键是找出原点的位置,然后根据平面直角坐标系的特点找出各个选项的正确坐标,即根据太和门的点的坐标为(0,-1),可得中和殿为原点(0,0),保和殿为(0,1),景仁宫(2,4),养心殿(-2,3),武英殿(-3.5,-3),所以只有B正确,故选B.
考点:点的坐标
10.B
【分析】根据对话画出图形,进而得出从邮局出发走到晓莉家的路线.
【详解】解:如图所示:从邮局出发走到晓莉家应:向北直走500米,再向西直走100米.
故选:B.
【点睛】此题主要考查了坐标确定位置,根据题意画出图形是解题关键.
11.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
12.D
【分析】利用平移变换的性质判断即可.
【详解】解:将某图形的各点的纵坐标减去2,横坐标加上1,可将该图形横向向右平移1个单位,纵向向下平移2个单位,
故选:D.
【点睛】本题考查平移变换的性质,解题的关键是理解平移变换的性质.
13.D
【分析】由于线段CD是由线段AB平移得到的,而点A(﹣1,4)的对应点为C(4,7),比较它们的坐标发现横坐标增加5,纵坐标增加3,利用此规律即可求出点D的对应点B的坐标.
【详解】解:∵线段CD是由线段AB平移得到的,
而点A(﹣1,4)的对应点为C(4,7),
∴由A平移到C点的横坐标增加5,纵坐标增加3,
则点D(-4,1)的对应点B的坐标为(﹣4-5, 1-3),即,
故选:D.
【点睛】本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
14.3
【分析】根据题目中定义的新坐标系中点坐标的表示方法,求出点C坐标,即可得到结果.
【详解】解:根据题意,点C的坐标应该是,
∴.
故答案是:3.
【点睛】本题考查新定义,解题的关键是理解题目中新定义的坐标系中点坐标的表示方法.
15.1
【分析】根据第一、三象限角平分线上点的坐标特征得到得3m﹣1=2m,然后解关于m的一次方程即可.
【详解】解:∵点A(3m﹣1,2m)在第一、三象限的角平分线上,
∴3m﹣1=2m,
解得:m=1.
故答案为:1
【点睛】此题考查象限及点的坐标的有关性质,解题关键在于掌握其定义列出方程.
16.
【分析】直接利用“帅”位于点,可得原点的位置,进而得出“兵”的坐标.
【详解】解:如图所示:可得原点位置,则“兵”位于.
故答案为.
【点睛】本题考查了直角坐标系、点的坐标,解题的关键是确定坐标系的原点的位置.
17.
【分析】根据A、B两点坐标找到原点坐标即可解答;
【详解】解:由,,可得平面直角坐标系如下图:
∴C点坐标(3,-1),
【点睛】本题考查了平面直角坐标系,掌握坐标的定义是解题关键.
18.或3
【分析】根据矩面积的定义表示出水平底”a和铅垂高“h,利用分类讨论对其铅垂高“h进行讨论,从而列出关于m的方程,解出方程即可求解.
【详解】∵D(2,2),E(-2,-1),F(3,m)
∴“水平底”a=3-(-2)=5
“铅垂高“h=3或|1+m|或|2-m|
①当h=3时,三点的“矩面积”S=5×3=15≠20,不合题意;
②当h=|1+m|时,三点的“矩面积”S=5×|1+m|=20,
解得:m=3或m=-5(舍去);
③当h=|2-m|时,三点的“矩面积”S=5×|2-m|=20,
解得:m=-2或m=6(舍去);
综上:m=3或-2
故答案为:3或-2
【点睛】本题考查坐标与图形的性质,解答本题的关键是明确题目中的新定义,利用新定义解答问题.
19.(2,-1).
【详解】试题分析:如图,根据A(-2,1)和B(-2,-3)确定平面直角坐标系,然后根据点C在坐标系中的位置确定点C的坐标为(2,-1).
考点:根据点的坐标确定平面直角坐标系.
20.(5,150°)
【分析】根据题意可得:圆圈数表示有序数对的第一个数,度数表示有序数对的第二个数,可得答案.
【详解】解:∵A,B的位置分别表示为(4,60°),(2,210°).
∴目标C的位置表示为(5,150°).
故答案为:(5,150°)
【点睛】本题考查了坐标确定位置,根据题意得到圆圈数表示有序数对的第一个数,度数表示有序数对的第二个数是解题关键.
21.(4,2)
【分析】根据A、B两点的坐标可得坐标的变化规律为横坐标加3,纵坐标加2,再把C点的坐标横坐标加3,纵坐标加2,即可求解.
【详解】解:∵将△ABC平移,使点B落在点A处,点A(1,2),B(﹣2,0),
∴坐标的变化规律为横坐标加3,纵坐标加2,
∵C(1,0),
∴点C的对应点的坐标为是(1+3,0+2),即(4,2).
故答案为:(4,2).
【点睛】本题考查了坐标系中的点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移过程中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
22.(1)当m=-1时,点M的坐标为(-2,1);当m=-2时,点M的坐标为(-3,-1);
(2)8
【分析】(1)根据点M到x轴的距离为1,得到,求出m即可;
(2)根据MN// x轴,得到2m+3=-1,求出点M的坐标,即可求出MN的长度.
【详解】(1)∵点M(m-1,2m+3),点M到x轴的距离为1,
∴,
解得,m=-1或m=-2,
当m=-1时,点M的坐标为(-2,1),
当m=-2时,点M的坐标为(-3,-1);
(2)∵点M(m-1,2m+3),点N(5,-1)且MN// x轴,
∴2m+3=-1,
解得:m=-2,
故点M的坐标为(-3,-1).
所以MN=5-(-3)=5+3=8.
【点睛】此题考查了点到坐标轴的距离,与坐标轴平行的直线上点的坐标特点,掌握并理解点的坐标与位置是解题的关键.
23.(1)16;(2)存在,或;(3).
【分析】(1)先根据偶次方的非负性、算术平方根的非负性可求出a、b的值,从而可得AB、BC的长,然后根据直角三角形的面积公式即可得;
(2)设点P的坐标为,从而可得,再根据点C的坐标可得PQ边上的高,然后利用三角形的面积公式可得一个关于m的绝对值方程,解方程即可得;
(3)如图(见解析),先根据平行线的判定与性质可得,,再根据角平分线的定义、角的和差可得,然后根据直角三角形的两锐角互余、等量代换即可得.
【详解】(1),
,
解得,
,
轴,
,
三角形的面积为;
(2)存在,求解过程如下:
设点P的坐标为,
,
,
,
三角形的PQ边上的高为4,
,
解得或,
故点P的坐标为或;
(3)如图,过点E作,
,
,
,
,
,分别平分,,
,
,
又轴轴,
,
.
【点睛】本题考查了偶次方的非负性、算术平方根的非负性、平行线的判定与性质、点坐标等知识点,较难的是题(3),通过作辅助线,利用到平行线的判定与性质是解题关键.
24.(1)(-4,-5).
(2)(-6,-6)或(2,-2)
【分析】(1)根据平行于x轴的直线上的点的纵坐标都相等列方程求解即可;
(2)点P到两坐标轴的距离相等,分两种情况讨论,即2m+4=m-1或2m+4+m-1=0,分别求出m的值,再求解P点坐标即可.
【详解】(1)由题意得,m-1=-5,解得m=-4,
∴2m+4=-4,则点P的坐标为(-4,-5).
(2)由题意得,2m+4=m-1或2m+4+m-1=0,解得m=-5或m=-1,
∴2m+4=-6,m-1=-6或2m +4=2,m-1=-2,
则点P的坐标为(-6,-6)或(2,-2).
【点睛】本题考查了平面直角坐标系中点的坐标的特征规律,熟练掌握知识点是解题的关键.
25.(1);;;特征:对应点的坐标的横纵坐标各互为相反数.(2).
【分析】(1)由图所示即可求出.
(2)根据(1)坐标的特征可得到关系、方程,解方程即可求出、的值.
【详解】(1)由图可得:;;,
由对应的的坐标可得:对应点的坐标的横纵坐标各互为相反数.
(2)由(1)中点的坐标特征可得,
点与点的横纵坐标互为相反数,
∴,
解得:.
【点睛】此题考查了坐标系中关于原点对称的点的坐标特点,解题的关键是熟练掌握坐标系中关于原点对称的点的坐标特点.
26.(1)作图见解析
(2)体育场的坐标是,火车站的坐标是,文化宫的坐标是;
(3)作图见解析
【分析】(1)根据超市的坐标与市场的坐标确定平面直角坐标系即可,如图1;
(2)在坐标系中确定点的坐标即可;
(3)根据坐标找出在直角坐标系中的位置描点即可,如图2.
(1)
解:根据超市的坐标是( 2,4),市场的坐标是(1,3),建立平面直角坐标系,如图1,
(2)
解:观察平面直角坐标系可知体育场、火车站和文化宫的坐标分别为:、和.
(3)
解:如图2,( 3, 2)在第三象限,建汽车站在第三象限如图,(2, 1)在第四象限,花坛在第四象限如图,
【点睛】本题考查了平面直角坐标系,坐标系描点,点坐标,有序数对表示位置.解题的关键在于熟练掌握平面直角坐标系.
27.(1)画图见解析;
(2)画图见解析,,
【分析】(1)根据即可画出;
(2)先画出平移后的,再写出点B1和点C1的坐标即可.
【详解】(1)解:如图所示:即为所求.
(2)解:平移后的如图所示:
此时,
【点睛】本题考查了作图-平移变换,掌握平移的性质是解决本题的关键.
28.(1)见解析
(2);;将向下平移4个单位,再向左平移2个单位得到新的三角形(答案不唯一)
(3)
【分析】(1)根据坐标,,描点,连接即可得;
(2)根据点A的平移方式确定的平移方式,从而得到点、点平移后的所得点的坐标和平移过程的描述;
(3)用长方形面积减去小三角形的面积即可得到的面积.
【详解】(1)如图,即为所求;
(2)由图可知,
点B平移后对应的坐标为:;点C平移后对应的坐标为:;
平移方式:将向下平移4个单位,再向左平移2个单位得到新的三角形(或将向左平移2个单位,再向下平移4个单位得到新的三角形;或将沿AO方向平移个单位长度得到新的三角形;答案不唯一);
(3).
【点睛】本题考查了坐标与图形中的描点、平移、求三角形的面积,熟练掌握点平移的坐标特征是本题的关键.
29.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
一、单选题
1.(2022春·山东聊城·七年级统考期末)2021年6月17日神舟十二号飞船于在甘肃酒泉发射升空,在太空驻留90天后于9月14日返回地球,下列描述能确定飞船着陆位置的是( )
A.内蒙古中部
B.酒泉卫星发射中心东南方向处
C.东经
D.北纬
2.(2022春·山东菏泽·七年级统考期末)在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )
A. B. C. D.
3.(2022春·山东临沂·七年级统考期末)在平面直角坐标系中,点B(2,3)到x轴的距离为( )
A.3 B.2 C.-3 D.-2
4.(2022春·山东滨州·七年级统考期末)已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·山东德州·七年级统考期末)下列语句正确的是( ).
A.在平面直角坐标系中,与表示两个不同的点
B.平行于轴的直线上所有点的横坐标都相同
C.若点在轴上,则
D.点到轴的距离为3
6.(2022春·山东聊城·七年级统考期末)在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )
A.1个 B.2个 C.3个 D.4个
7.(2022春·山东济宁·七年级统考期末)如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2022个点的坐标为( )
A. B. C. D.
8.(2022春·山东德州·七年级统考期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,是一局象棋残局,若表示棋子“炮”和“車”的点的坐标分别为(1,2),(﹣2,0),则表示棋子“馬”的点的坐标为( )
A.(﹣3,3) B.(﹣3,2) C.(4,2) D.(3,2)
9.(2022春·山东泰安·七年级校考期末)如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2) B.养心殿(-2,3)
C.保和殿(1,0) D.武英殿(-3.5,-4)
10.(2022春·山东潍坊·七年级统考期末)下图为小莉与小莹的微信对话记录.据图中两个人的对话记录,有一种走法能从邮局出发走到小莉家,此走法为( )
A.向北直走400米,再向东直走300米 B.向北直走500米,再向西直走100米
C.向北直走100米,再向西直走500米 D.向北直走200米,再向东直走300米
11.(2022春·山东临沂·七年级统考期末)在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
12.(2022春·山东临沂·七年级统考期末)将某图形的各点的纵坐标减去2,横坐标加上1,可将该图形( )
A.横向向左平移2个单位,纵向向上平移2个单位
B.横向向左平移1个单位,纵向向下平移2个单位
C.横向向右平移1个单位,纵向向上平移2个单位
D.横向向右平移1个单位,纵向向下平移2个单位
13.(2022春·山东滨州·七年级统考期末)线段是由线段平移得到的,点的对应点为,则的对应点B的坐标为( ).
A. B. C. D.
二、填空题
14.(2022春·山东德州·七年级统考期末)如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号),如点A的坐标可表示为,点B的坐标可表示为,按此方法,若点C的坐标为,则m=__________.
15.(2022春·山东德州·七年级统考期末)点A(3m﹣1,2m)位于第一、三象限的角平分线上,则m=_____.
16.(2022春·山东济宁·七年级统考期末)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于点__________.
17.(2022春·山东德州·七年级统考期末)如图,利用平面直角坐标系画出的正方形网格中,若,,则点的坐标为________.
18.(2022春·山东济宁·七年级统考期末)在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
19.(2022春·山东德州·七年级统考期末)如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是_____.
20.(2022春·山东聊城·七年级统考期末)如图,雷达探测器测得A,B,C三个目标,如果A,B的位置分别表示为(4,60°),(2,210°).则目标C的位置表示为______.
21.(2022春·山东济宁·七年级统考期末)如图,已知Rt△ABC的边BC在x轴上,,且A(1,2),B(-2,0)若将△ABC平移,使点B落在点A处,则点C的对应点的坐标为___________
三、解答题
22.(2022春·山东滨州·七年级统考期末)已知平面直角坐标系中有一点.
(1)若点M到x轴的距离为1,请求出点M的坐标.
(2)若点),且轴,求线段的长度.
23.(2022春·山东济宁·七年级统考期末)如图①,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由.
(3)若过作交轴于,且,分别平分,,如图②,求的度数.
24.(2022春·山东菏泽·七年级统考期末)在平面直角坐标系中,已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.
(1)点P在过A(2,-5)点,且与x轴平行的直线上;
(2)点P到两坐标轴的距离相等;
25.(2022春·山东临沂·七年级统考期末)如图,、经过某种变换得到的图形,点与点,点与点,点与点分别是对应点.
(1)分别写出点与点,点与点,点与点的坐标,并说说对应点的坐标有哪些特征;
(2)若点与点也是通过上述变换得到的对应点,求、的值.
26.(2022春·山东聊城·七年级统考期末)如图是某市火车站及周围的平面示意图,已知超市的坐标是,市场的坐标是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出体育场、火车站和文化宫的坐标;
(3)准备在处建汽车站,在处建花坛,请你标出汽车站和花坛的位置.
27.(2022春·山东济宁·七年级统考期末)在平面直角坐标系中,的三个顶点坐标分别是.
(1)画出;
(2)将平移,使点A平移到原点O,画出平移后的图形并写出点B和点C的对应点坐标.
28.(2022春·山东德州·七年级统考期末)在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)在平面直角坐标系中画出;
(2)平移,使点A与点重合,写出点、点平移后的所得点的坐标,并描述这个平移过程.
(3)求的面积
29.(2022春·山东滨州·七年级统考期末)如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
参考答案:
1.B
【分析】根据坐标确定位置需要两个数据解答.
【详解】解:酒泉卫星发射中心东南方向1000km处能确定位置.
故选:B.
【点睛】本题考查了确定位置,理解确定位置需要两个数据是解题的关键.
2.D
【分析】根据点到坐标轴的距离及点所在的象限解答即可.
【详解】解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:D.
【点睛】此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
3.A
【分析】根据点的纵坐标的绝对值是点到x轴的距离即可得答案.
【详解】解:在平面直角坐标系中,点(2,3)到x轴的距离为3.
故选:A.
【点睛】本题考查了点的坐标,熟练掌握点的纵坐标的绝对值是点到x轴的距离是解题的关键.
4.C
【分析】根据直线ABx轴可得点A、B的纵坐标相等可求出a的值,根据点P在x轴的负半轴上,得到b<0,然后判断点M的横坐标与纵坐标的正负即可解答.
【详解】解:∵直线ABx轴,
∴2a+2=4,解得:a=1,
∵点P在x轴的负半轴上,
∴b<0,
∴b-a=b-1<0,a-2=1-2=-1<0,
.点M在第三象限.
故选:C.
【点睛】本题主要考查了坐标与图形性质,根据直线ABx轴可得点A,B的纵坐标相等是解答本题的关键.
5.A
【分析】根据平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点逐一判断即可得.
【详解】A.在平面直角坐标系中, ( 3,5) 与 (5, 3) 表示两个不同的点,此选项正确,符合题意;
B.平行于 x 轴的直线上所有点的纵坐标都相同,此选项错误,不符合题意;
C.若点 P(a,b) 在 y 轴上,则a=0 ,此选项错误,不符合题意;
D.点 P( 3,4) 到 x 轴的距离为4,此选项错误,不符合题意;
故选:A.
【点睛】本题主要考查坐标与图形的性质,解题的关键是掌握平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点.
6.D
【分析】分类讨论:当C点在y轴上,设C(0,t),根据三角形面积公式得到 |t﹣3| 2=6,当C点在x轴上,设C(m,0),根据三角形面积公式得到|m+2| 3=6,然后分别解绝对值方程求出t和m即可得到C点坐标.
【详解】解:分两种情况:
①当C点在y轴上,设C(0,t),
∵三角形ABC的面积为6,
∴ |t﹣3| 2=6,
解得t=9或﹣3.
∴C点坐标为(0,﹣3),(0,9),
②当C点在x轴上,设C(m,0),
∵三角形ABC的面积为6,
∴ |m+2| 3=6,
解得m=2或﹣6.
∴C点坐标为(2,0),(﹣6,0),
综上所述,C点有4个.
故选:D.
【点睛】此题重点考查学生对平面直角坐标系上的点的应用,掌握平面直角坐标系的点的性质是解题的关键.
7.C
【分析】以正方形最外边上的点为准考虑,点的总个数等于最右下角的点横坐标n的平方,且横坐标n为奇数时最后一个点在x轴上,n为偶数时,最后一个点坐标为(1,n-1),求出与2022最接近的平方数为2025,然后根据上述规律写出第2022个点的坐标即可.
【详解】解:由图形可知,图中各点分别组成了正方形点阵,每个正方形点阵的整点数量依次为最右下角点横坐标的平方,且当正方形最右下角点的横坐标为奇数时,这个点可以看做按照运动方向到达x轴,当正方形最右下角点的横坐标为偶数时,这个点可以看作按照运动方向离开x轴,
∵452=2025,
∴第2025个点在x轴上坐标为(45,0),
则第2022个点坐标为(45,3),
故答案为:C.
【点睛】本题考查了点的坐标,观察出点的个数与横坐标存在平方关系是解题的关键,解答时除了注意点坐标的变化外,还要注意点的运动方向.
8.C
【分析】根据棋子“炮”和“車”的点坐标,推断出原点位置,进而可得出“馬”的点的坐标.
【详解】解:如图所示,根据“車”的点坐标为,可知轴在“車”所在的横线上,
又根据“炮”的点坐标,可推出原点坐标如图所示,
进而可知“馬”的点的坐标为.
故选:C.
【点睛】本题综合考查点的坐标位置的确定.解答本题的关键是由“炮”和“車”的点坐标确定出原点的坐标.
9.B
【详解】试题分析:本题考查了点的坐标问题,解题关键是找出原点的位置,然后根据平面直角坐标系的特点找出各个选项的正确坐标,即根据太和门的点的坐标为(0,-1),可得中和殿为原点(0,0),保和殿为(0,1),景仁宫(2,4),养心殿(-2,3),武英殿(-3.5,-3),所以只有B正确,故选B.
考点:点的坐标
10.B
【分析】根据对话画出图形,进而得出从邮局出发走到晓莉家的路线.
【详解】解:如图所示:从邮局出发走到晓莉家应:向北直走500米,再向西直走100米.
故选:B.
【点睛】此题主要考查了坐标确定位置,根据题意画出图形是解题关键.
11.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
12.D
【分析】利用平移变换的性质判断即可.
【详解】解:将某图形的各点的纵坐标减去2,横坐标加上1,可将该图形横向向右平移1个单位,纵向向下平移2个单位,
故选:D.
【点睛】本题考查平移变换的性质,解题的关键是理解平移变换的性质.
13.D
【分析】由于线段CD是由线段AB平移得到的,而点A(﹣1,4)的对应点为C(4,7),比较它们的坐标发现横坐标增加5,纵坐标增加3,利用此规律即可求出点D的对应点B的坐标.
【详解】解:∵线段CD是由线段AB平移得到的,
而点A(﹣1,4)的对应点为C(4,7),
∴由A平移到C点的横坐标增加5,纵坐标增加3,
则点D(-4,1)的对应点B的坐标为(﹣4-5, 1-3),即,
故选:D.
【点睛】本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
14.3
【分析】根据题目中定义的新坐标系中点坐标的表示方法,求出点C坐标,即可得到结果.
【详解】解:根据题意,点C的坐标应该是,
∴.
故答案是:3.
【点睛】本题考查新定义,解题的关键是理解题目中新定义的坐标系中点坐标的表示方法.
15.1
【分析】根据第一、三象限角平分线上点的坐标特征得到得3m﹣1=2m,然后解关于m的一次方程即可.
【详解】解:∵点A(3m﹣1,2m)在第一、三象限的角平分线上,
∴3m﹣1=2m,
解得:m=1.
故答案为:1
【点睛】此题考查象限及点的坐标的有关性质,解题关键在于掌握其定义列出方程.
16.
【分析】直接利用“帅”位于点,可得原点的位置,进而得出“兵”的坐标.
【详解】解:如图所示:可得原点位置,则“兵”位于.
故答案为.
【点睛】本题考查了直角坐标系、点的坐标,解题的关键是确定坐标系的原点的位置.
17.
【分析】根据A、B两点坐标找到原点坐标即可解答;
【详解】解:由,,可得平面直角坐标系如下图:
∴C点坐标(3,-1),
【点睛】本题考查了平面直角坐标系,掌握坐标的定义是解题关键.
18.或3
【分析】根据矩面积的定义表示出水平底”a和铅垂高“h,利用分类讨论对其铅垂高“h进行讨论,从而列出关于m的方程,解出方程即可求解.
【详解】∵D(2,2),E(-2,-1),F(3,m)
∴“水平底”a=3-(-2)=5
“铅垂高“h=3或|1+m|或|2-m|
①当h=3时,三点的“矩面积”S=5×3=15≠20,不合题意;
②当h=|1+m|时,三点的“矩面积”S=5×|1+m|=20,
解得:m=3或m=-5(舍去);
③当h=|2-m|时,三点的“矩面积”S=5×|2-m|=20,
解得:m=-2或m=6(舍去);
综上:m=3或-2
故答案为:3或-2
【点睛】本题考查坐标与图形的性质,解答本题的关键是明确题目中的新定义,利用新定义解答问题.
19.(2,-1).
【详解】试题分析:如图,根据A(-2,1)和B(-2,-3)确定平面直角坐标系,然后根据点C在坐标系中的位置确定点C的坐标为(2,-1).
考点:根据点的坐标确定平面直角坐标系.
20.(5,150°)
【分析】根据题意可得:圆圈数表示有序数对的第一个数,度数表示有序数对的第二个数,可得答案.
【详解】解:∵A,B的位置分别表示为(4,60°),(2,210°).
∴目标C的位置表示为(5,150°).
故答案为:(5,150°)
【点睛】本题考查了坐标确定位置,根据题意得到圆圈数表示有序数对的第一个数,度数表示有序数对的第二个数是解题关键.
21.(4,2)
【分析】根据A、B两点的坐标可得坐标的变化规律为横坐标加3,纵坐标加2,再把C点的坐标横坐标加3,纵坐标加2,即可求解.
【详解】解:∵将△ABC平移,使点B落在点A处,点A(1,2),B(﹣2,0),
∴坐标的变化规律为横坐标加3,纵坐标加2,
∵C(1,0),
∴点C的对应点的坐标为是(1+3,0+2),即(4,2).
故答案为:(4,2).
【点睛】本题考查了坐标系中的点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移过程中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
22.(1)当m=-1时,点M的坐标为(-2,1);当m=-2时,点M的坐标为(-3,-1);
(2)8
【分析】(1)根据点M到x轴的距离为1,得到,求出m即可;
(2)根据MN// x轴,得到2m+3=-1,求出点M的坐标,即可求出MN的长度.
【详解】(1)∵点M(m-1,2m+3),点M到x轴的距离为1,
∴,
解得,m=-1或m=-2,
当m=-1时,点M的坐标为(-2,1),
当m=-2时,点M的坐标为(-3,-1);
(2)∵点M(m-1,2m+3),点N(5,-1)且MN// x轴,
∴2m+3=-1,
解得:m=-2,
故点M的坐标为(-3,-1).
所以MN=5-(-3)=5+3=8.
【点睛】此题考查了点到坐标轴的距离,与坐标轴平行的直线上点的坐标特点,掌握并理解点的坐标与位置是解题的关键.
23.(1)16;(2)存在,或;(3).
【分析】(1)先根据偶次方的非负性、算术平方根的非负性可求出a、b的值,从而可得AB、BC的长,然后根据直角三角形的面积公式即可得;
(2)设点P的坐标为,从而可得,再根据点C的坐标可得PQ边上的高,然后利用三角形的面积公式可得一个关于m的绝对值方程,解方程即可得;
(3)如图(见解析),先根据平行线的判定与性质可得,,再根据角平分线的定义、角的和差可得,然后根据直角三角形的两锐角互余、等量代换即可得.
【详解】(1),
,
解得,
,
轴,
,
三角形的面积为;
(2)存在,求解过程如下:
设点P的坐标为,
,
,
,
三角形的PQ边上的高为4,
,
解得或,
故点P的坐标为或;
(3)如图,过点E作,
,
,
,
,
,分别平分,,
,
,
又轴轴,
,
.
【点睛】本题考查了偶次方的非负性、算术平方根的非负性、平行线的判定与性质、点坐标等知识点,较难的是题(3),通过作辅助线,利用到平行线的判定与性质是解题关键.
24.(1)(-4,-5).
(2)(-6,-6)或(2,-2)
【分析】(1)根据平行于x轴的直线上的点的纵坐标都相等列方程求解即可;
(2)点P到两坐标轴的距离相等,分两种情况讨论,即2m+4=m-1或2m+4+m-1=0,分别求出m的值,再求解P点坐标即可.
【详解】(1)由题意得,m-1=-5,解得m=-4,
∴2m+4=-4,则点P的坐标为(-4,-5).
(2)由题意得,2m+4=m-1或2m+4+m-1=0,解得m=-5或m=-1,
∴2m+4=-6,m-1=-6或2m +4=2,m-1=-2,
则点P的坐标为(-6,-6)或(2,-2).
【点睛】本题考查了平面直角坐标系中点的坐标的特征规律,熟练掌握知识点是解题的关键.
25.(1);;;特征:对应点的坐标的横纵坐标各互为相反数.(2).
【分析】(1)由图所示即可求出.
(2)根据(1)坐标的特征可得到关系、方程,解方程即可求出、的值.
【详解】(1)由图可得:;;,
由对应的的坐标可得:对应点的坐标的横纵坐标各互为相反数.
(2)由(1)中点的坐标特征可得,
点与点的横纵坐标互为相反数,
∴,
解得:.
【点睛】此题考查了坐标系中关于原点对称的点的坐标特点,解题的关键是熟练掌握坐标系中关于原点对称的点的坐标特点.
26.(1)作图见解析
(2)体育场的坐标是,火车站的坐标是,文化宫的坐标是;
(3)作图见解析
【分析】(1)根据超市的坐标与市场的坐标确定平面直角坐标系即可,如图1;
(2)在坐标系中确定点的坐标即可;
(3)根据坐标找出在直角坐标系中的位置描点即可,如图2.
(1)
解:根据超市的坐标是( 2,4),市场的坐标是(1,3),建立平面直角坐标系,如图1,
(2)
解:观察平面直角坐标系可知体育场、火车站和文化宫的坐标分别为:、和.
(3)
解:如图2,( 3, 2)在第三象限,建汽车站在第三象限如图,(2, 1)在第四象限,花坛在第四象限如图,
【点睛】本题考查了平面直角坐标系,坐标系描点,点坐标,有序数对表示位置.解题的关键在于熟练掌握平面直角坐标系.
27.(1)画图见解析;
(2)画图见解析,,
【分析】(1)根据即可画出;
(2)先画出平移后的,再写出点B1和点C1的坐标即可.
【详解】(1)解:如图所示:即为所求.
(2)解:平移后的如图所示:
此时,
【点睛】本题考查了作图-平移变换,掌握平移的性质是解决本题的关键.
28.(1)见解析
(2);;将向下平移4个单位,再向左平移2个单位得到新的三角形(答案不唯一)
(3)
【分析】(1)根据坐标,,描点,连接即可得;
(2)根据点A的平移方式确定的平移方式,从而得到点、点平移后的所得点的坐标和平移过程的描述;
(3)用长方形面积减去小三角形的面积即可得到的面积.
【详解】(1)如图,即为所求;
(2)由图可知,
点B平移后对应的坐标为:;点C平移后对应的坐标为:;
平移方式:将向下平移4个单位,再向左平移2个单位得到新的三角形(或将向左平移2个单位,再向下平移4个单位得到新的三角形;或将沿AO方向平移个单位长度得到新的三角形;答案不唯一);
(3).
【点睛】本题考查了坐标与图形中的描点、平移、求三角形的面积,熟练掌握点平移的坐标特征是本题的关键.
29.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
