第19章+四边形-矩形的性质课件+2022--2023学年沪科版八年级下册数学 21张PPT
文档属性
| 名称 | 第19章+四边形-矩形的性质课件+2022--2023学年沪科版八年级下册数学 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 19:36:42 | ||
图片预览




文档简介
(共21张PPT)
19.3
矩形性质
理解矩形的概念,知道矩形与平行四边形的区别与联系.
会证明矩形的性质,会用矩形的性质解决简单的问题.
学习目标
思考
矩形跟我们前面学行四边形有什么关系?
思考
由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
因为矩形是平行四边形,所以它具有平行四边形的所有性质
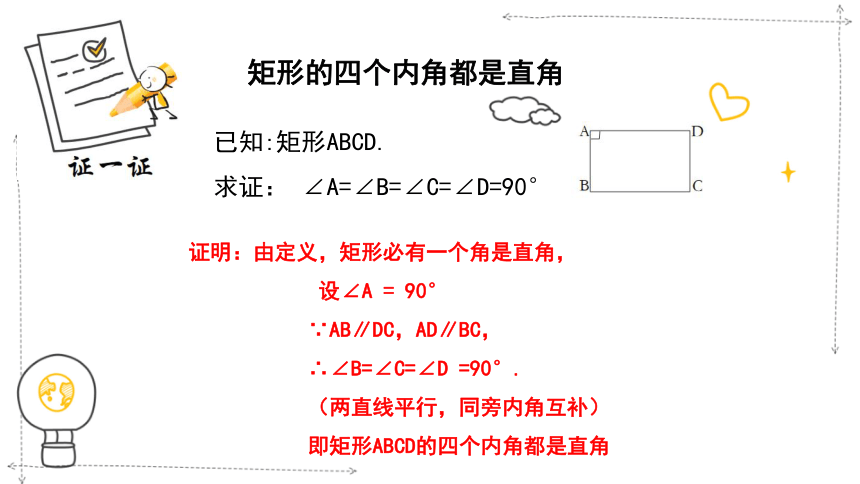
矩形的四个内角都是直角
已知:矩形ABCD.
求证: ∠A=∠B=∠C=∠D=90°
证明:由定义,矩形必有一个角是直角,
设∠A = 90°
∵AB∥DC,AD∥BC,
∴∠B=∠C=∠D =90°.
(两直线平行,同旁内角互补)
即矩形ABCD的四个内角都是直角
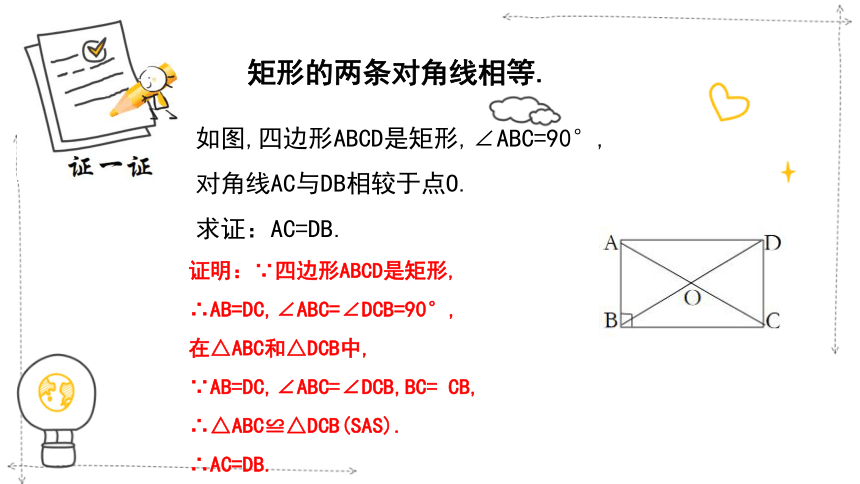
矩形的两条对角线相等.
如图,四边形ABCD是矩形,∠ABC=90°,
对角线AC与DB相较于点O.
求证:AC=DB.
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
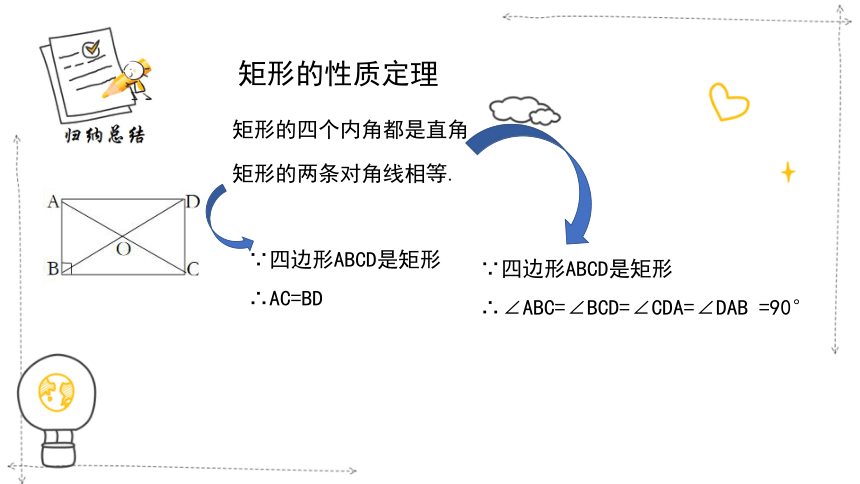
矩形的性质定理
矩形的四个内角都是直角
矩形的两条对角线相等.
∵四边形ABCD是矩形
∴AC=BD
∵四边形ABCD是矩形
∴∠ABC=∠BCD=∠CDA=∠DAB =90°
类比思考 探究性质
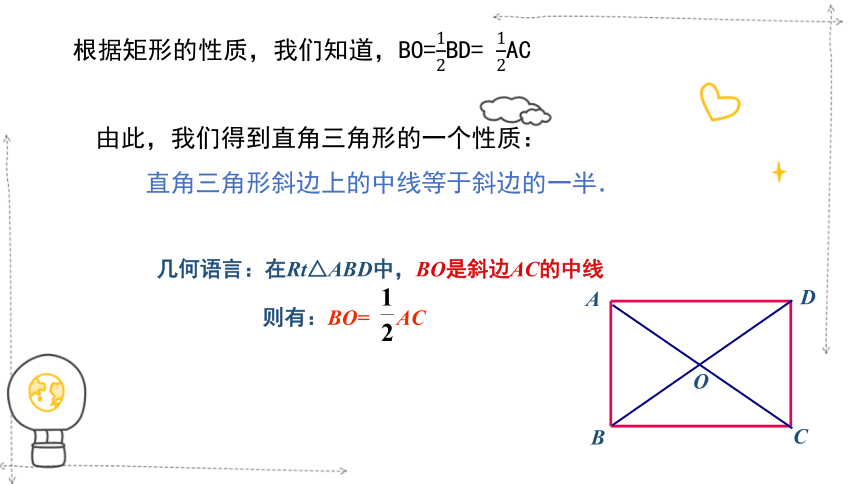
根据矩形的性质,我们知道,BO=BD= AC
由此,我们得到直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
几何语言:在Rt△ABD中,BO是斜边AC的中线
则有:BO= AC
A
B
C
D
O
类比思考 探究性质
三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗 请说明理由.
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
典例精讲
例1 矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=4cm,求矩形的两条对角线的长.
解:∵四边形ABCD是矩形
∴AC=BD,AO=CO=BO=DO
∵∠AOD=120°
∴∠AOB=60°
∴△AOB是等边三角形
∴AO=BO=AB=4cm
∴AC=BD=2OA=8(cm)
即矩形ABCD对角线的长为8cm.
例2 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC
典例精讲
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°
又∵DE=DE,
∴△DFE≌△DCE(AAS),
∴DF=DC.
典例精讲
例3 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED=DE·AB= ×5×4=10.
矩形的折叠问题常与勾股定理结合考查。
挑战自我
1.如图,在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
C
挑战自我
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
挑战自我
3.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
挑战自我
4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(1)证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
挑战自我
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.
(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC= ==
∴四边形ABED的面积= ×(4+8)×=24.
挑战自我
5.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,∴PE+PF= .
课堂小结
谈谈你的收获。
感谢您的聆听!
19.3
矩形性质
理解矩形的概念,知道矩形与平行四边形的区别与联系.
会证明矩形的性质,会用矩形的性质解决简单的问题.
学习目标
思考
矩形跟我们前面学行四边形有什么关系?
思考
由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
因为矩形是平行四边形,所以它具有平行四边形的所有性质
矩形的四个内角都是直角
已知:矩形ABCD.
求证: ∠A=∠B=∠C=∠D=90°
证明:由定义,矩形必有一个角是直角,
设∠A = 90°
∵AB∥DC,AD∥BC,
∴∠B=∠C=∠D =90°.
(两直线平行,同旁内角互补)
即矩形ABCD的四个内角都是直角
矩形的两条对角线相等.
如图,四边形ABCD是矩形,∠ABC=90°,
对角线AC与DB相较于点O.
求证:AC=DB.
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB(SAS).
∴AC=DB.
矩形的性质定理
矩形的四个内角都是直角
矩形的两条对角线相等.
∵四边形ABCD是矩形
∴AC=BD
∵四边形ABCD是矩形
∴∠ABC=∠BCD=∠CDA=∠DAB =90°
类比思考 探究性质
根据矩形的性质,我们知道,BO=BD= AC
由此,我们得到直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
几何语言:在Rt△ABD中,BO是斜边AC的中线
则有:BO= AC
A
B
C
D
O
类比思考 探究性质
三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗 请说明理由.
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
典例精讲
例1 矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=4cm,求矩形的两条对角线的长.
解:∵四边形ABCD是矩形
∴AC=BD,AO=CO=BO=DO
∵∠AOD=120°
∴∠AOB=60°
∴△AOB是等边三角形
∴AO=BO=AB=4cm
∴AC=BD=2OA=8(cm)
即矩形ABCD对角线的长为8cm.
例2 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC
典例精讲
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE,
∴∠DFE=∠C=90°
又∵DE=DE,
∴△DFE≌△DCE(AAS),
∴DF=DC.
典例精讲
例3 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED=DE·AB= ×5×4=10.
矩形的折叠问题常与勾股定理结合考查。
挑战自我
1.如图,在矩形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
C
挑战自我
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
挑战自我
3.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
挑战自我
4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(1)证明:∵四边形ABCD是矩形,
∴AC= BD, AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
挑战自我
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.
(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC= ==
∴四边形ABED的面积= ×(4+8)×=24.
挑战自我
5.如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值.
解:连接OP.
∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OC=OB,
S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD= ×6×8=12.
在Rt△BAD中,由勾股定理得BD=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴ AO·PE+ DO·PF=12,即5PE+5PF=24,∴PE+PF= .
课堂小结
谈谈你的收获。
感谢您的聆听!
