第七章:平面直角坐标系练习题2021-2022学年山西省七年级下学期人教版数学期末试题选编 含解析
文档属性
| 名称 | 第七章:平面直角坐标系练习题2021-2022学年山西省七年级下学期人教版数学期末试题选编 含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 19:53:05 | ||
图片预览



文档简介
第七章:平面直角坐标系 练习题
一、单选题
1.(2022春·山西忻州·七年级统考期末)家长会前,四个孩子分别向家长描述自己在班里的座位,家长能准确找到自己孩子座位的是( )
A.小明说他坐在第1排 B.小白说他坐在第3列 C.小清说她坐在第2排第5列 D.小楚说他的座位靠窗
2.(2022春·山西忻州·七年级统考期末)已知A点的坐标为(3,a+3),B点的坐标为(a,4),AB∥x轴,则线段AB的长为( )
A.5 B.4 C.3 D.2
3.(2022春·山西吕梁·七年级统考期末)若点A(,)在第二、四象限的平分线上,则点A的坐标为( )
A.(5,-5) B.(-5,-5) C.(5,5) D.(-5,5)
4.(2022春·山西朔州·七年级统考期末)如图的坐标平面上有原点与、、、四点.若有一直线通过点且与轴垂直,则也会通过下列哪一点?( )
A. B. C. D.
5.(2022春·山西临汾·七年级统考期末)下列四个点中,在平面直角坐标系内位于轴上的点是( )
A.(0,2022) B.(2022,0) C.(2022,2) D.(-2,-2022)
6.(2022春·山西临汾·七年级统考期末)在平面直角坐标系的第四象限内有一点,到轴的距离为4,到轴的距离为5,则点的坐标为( )
A. B. C. D.
7.(2022春·山西大同·七年级统考期末)在平面直角坐标系中,点A的坐标是(3a﹣9,a﹣2),则下列说法正确的是( )
A.当点A在x轴上时,a=3 B.当点A在y轴上时,a=2
C.当a>3时,点A在第一象限 D.当a<2时,点A在第二象限
8.(2022春·山西吕梁·七年级统考期末)中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用表示“炮”的位置,表示“士”的位置,那么“将”的位置应表示为( )
A. B. C. D.
9.(2022春·山西吕梁·七年级统考期末)在平面直角坐标系中,点在第四象限,且,将点A向左平移3个单位长度后得到点,则点的坐标是( )
A. B. C. D.
10.(2022春·山西忻州·七年级统考期末)点向下平移2个单位长度,得到的点的坐标是( )
A. B. C. D.
二、填空题
11.(2022春·山西忻州·七年级统考期末)已知P点坐标为(4-a,3a+9),且点P在轴上,则点P的坐标是______.
12.(2022春·山西忻州·七年级统考期末)如图,直角坐标平面xoy内,动点P按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),…按这样的运动规律,动点P第2022次运动到点的坐标是_____.
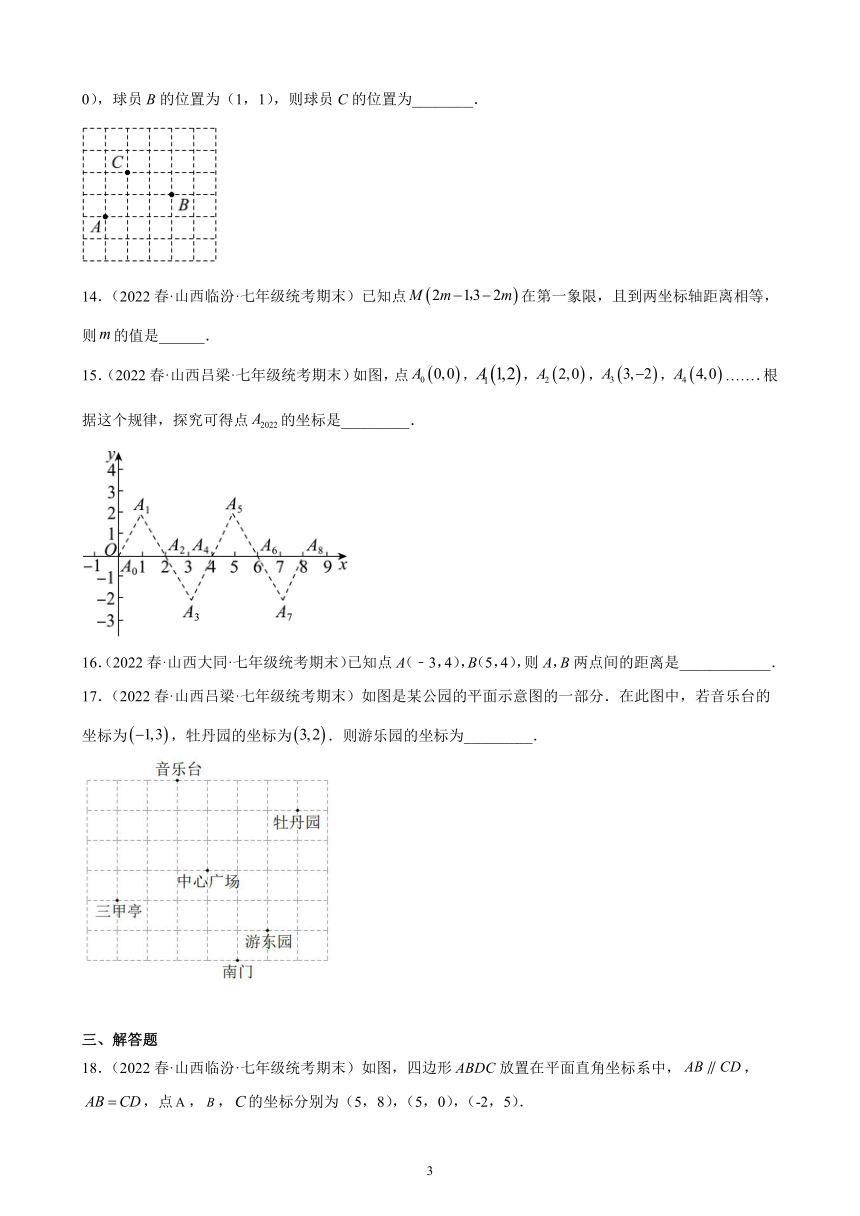
13.(2022春·山西吕梁·七年级统考期末)如图是一足球场的半场平面示意图,已知球员A的位置为(-2,0),球员B的位置为(1,1),则球员C的位置为________.
14.(2022春·山西临汾·七年级统考期末)已知点在第一象限,且到两坐标轴距离相等,则的值是______.
15.(2022春·山西吕梁·七年级统考期末)如图,点,,,,…….根据这个规律,探究可得点的坐标是_________.
16.(2022春·山西大同·七年级统考期末)已知点A(﹣3,4),B(5,4),则A,B两点间的距离是____________.
17.(2022春·山西吕梁·七年级统考期末)如图是某公园的平面示意图的一部分.在此图中,若音乐台的坐标为,牡丹园的坐标为.则游乐园的坐标为_________.
三、解答题
18.(2022春·山西临汾·七年级统考期末)如图,四边形放置在平面直角坐标系中,,,点,,的坐标分别为(5,8),(5,0),(-2,5).
(1)与轴的位置关系是______(填“平行”或“相交”),点的坐标为______;
(2)是线段上一动点,则距离的最小值______,距离最小时,点的坐标是______;
(3),分别是线段,上的动点,从出发向点运动,速度为每秒个单位长度,从出发向点运动,速度为每秒个单位长度,若两点同时出发,几秒后、两点距离恰好为?
19.(2022春·山西吕梁·七年级统考期末)平面直角坐标系是由原点重合且互相垂直的两条数轴构成的,它是沟通代数与几何的桥梁,是非常重要的数学工具.
(1)最早引入坐标系,用代数方法研究几何图形的数学家是( )
A.祖冲之 B.刘徽 C.笛卡尔 D.欧几里得
(2)在数学活动课上,老师与同学们一起探究如下问题:
在平面直角坐标系中的位置如图,已知点的坐标为.把向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的.
①写出点的坐标_________,的坐标_________;
②在轴上找一点,使的面积等于3,求满足条件的点的坐标;
③在解决问题②时用到的数学思想是__________________(填一个即可)
20.(2022春·山西忻州·七年级统考期末)如图,在平面直角坐标系中,已知△ABC中,点A坐标为(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)写出点C的坐标( , )
(2)在y轴上是否存在点P,使得S△POB=S△ABC,若存在,求出点P的坐标;若不存在;
(3)把点C往上平移3个单位得到点H,画射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探索∠BMA、∠HBM、∠MAC之间的数量关系,并证明你的结论.
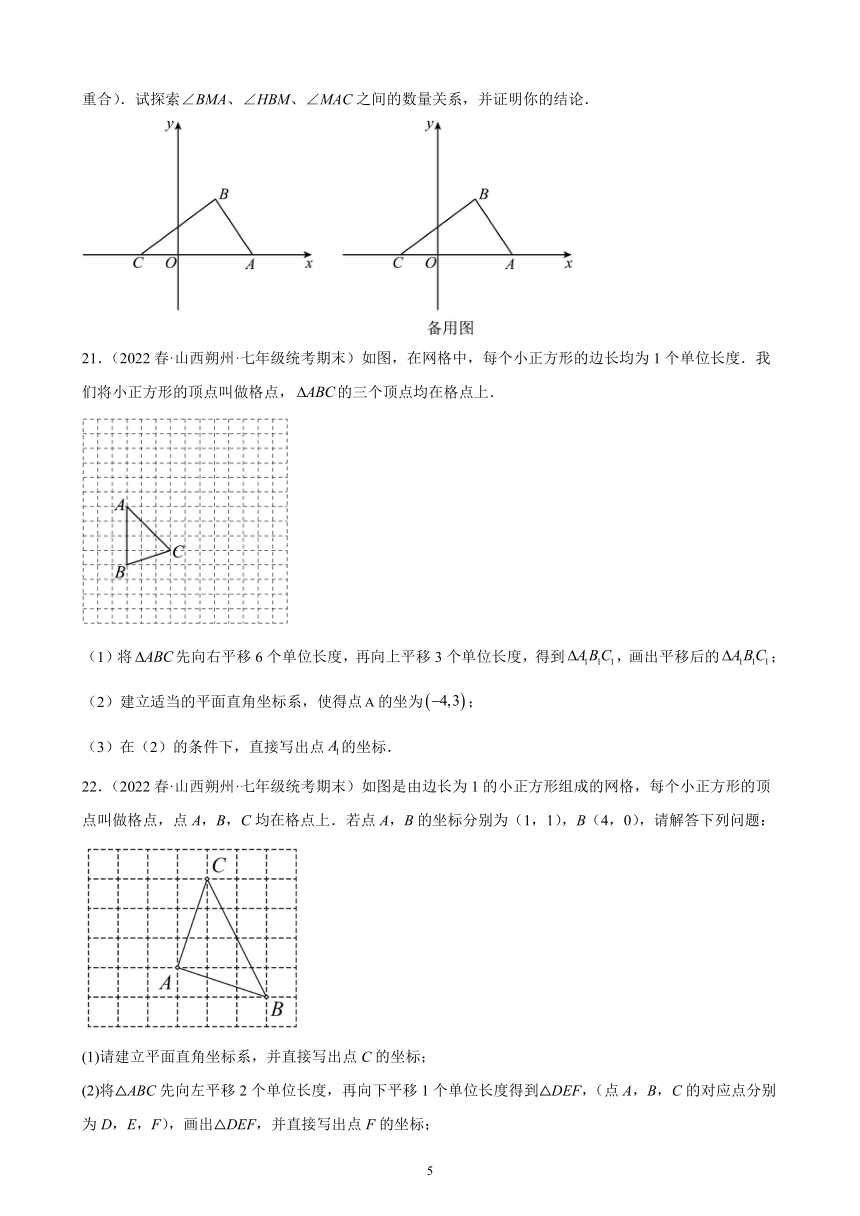
21.(2022春·山西朔州·七年级统考期末)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,的三个顶点均在格点上.
(1)将先向右平移6个单位长度,再向上平移3个单位长度,得到,画出平移后的;
(2)建立适当的平面直角坐标系,使得点的坐为;
(3)在(2)的条件下,直接写出点的坐标.
22.(2022春·山西朔州·七年级统考期末)如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点A,B,C均在格点上.若点A,B的坐标分别为(1,1),B(4,0),请解答下列问题:
(1)请建立平面直角坐标系,并直接写出点C的坐标;
(2)将△ABC先向左平移2个单位长度,再向下平移1个单位长度得到△DEF,(点A,B,C的对应点分别为D,E,F),画出△DEF,并直接写出点F的坐标;
(3)直接写出(2)中四边形DBCF的面积为________.
23.(2022春·山西大同·七年级统考期末)如图,在平面直角坐标系中,三角形ABC的三个顶点都在网格的格点上,其中点C的坐标为(1,2).
(1)点A的坐标为____________,点B的坐标为____________;
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',请画出平移后的三角形A'B'C',并写出点A',B',C'的坐标.
24.(2022春·山西大同·七年级统考期末)综合与探究
在平面直角坐标系中,点A在第四象限,将线段AO平移至线段BC的位置,点A的对应点是点B,点O的对应点是点C.
(1)如图①,点A的坐标是(2,﹣3),点B的坐标是(﹣3,0),连接OC.若在y轴上存在一点P,使得三角形COP的面积是三角形OBC的面积的2倍,求点P的坐标.
(2)如图②,当点C在y轴的正半轴上,点D在y轴的负半轴上,且∠ADB=90°时,试猜想∠CBD与∠OAD的数量关系,并说明理由.
25.(2022春·山西吕梁·七年级统考期末)如图,已知A(-2,0),C(1,4),点B在轴的正半轴上,已知△ABC的面积为10.
(1)求点B的坐标,并画出△ABC;
(2)将△ABC先向右平移3个单位长度,再向下平移5个单位长度,画出平移后的,并写出,,的坐标.
26.(2022春·山西吕梁·七年级统考期末)如图,平面直角坐标中,三角形的三个顶点坐标分别为,,.
(1)将三角形先向右平移4个单位,再向下平移2个单位,在平面直角坐标系中画出平移后的三角形;
(2)直接写出三角形的面积为_________.
参考答案:
1.C
【分析】直接利用坐标确定位置需要两个量,进而分析得出答案.
【详解】解:A.小明说他坐在第1排,无法确定座位位置,故此选项不合题意;
B.小白说他坐在第3列,无法确定座位位置,故此选项不合题意;
C.小清说她坐在第2排第5列,可以确定座位位置,故此选项符合题意;
D.小楚说他的座位靠窗,无法确定座位位置,故此选项不合题意;
故选:C.
【点睛】本题主要考查了坐标确定位置,掌握具体位置确定需两个量是解题关键.
2.D
【分析】先根据轴,求出a的值,再求出AB的长即可.
【详解】∵轴,
∴a+3=4,
解得a=1.
∴点A(3,4),点B(1,4),
∴AB=3-1=2.
故选:D.
【点睛】本题主要考查了平面直角坐标系内点的特征,根据轴求出a值是解题的关键.
3.A
【分析】根据二、四象限角平分线上的点横坐标与纵坐标互为相反数列得关于m的方程求得m的值,进而确定A的坐标.
【详解】解:∵A(3+m,m-7)在第二、四象限的平分线上,
∴(3+m)+(m-7)=0,解得m=2,
∴3+m=5,m-7=-5,
∴A的坐标为(5,-5).
故选:A.
【点睛】本题主要考查了点的坐标、解一元一次方程等知识点,根据二、四象限角平分线上的点横坐标与纵坐标互为相反数列出关于m的方程是解本答题的关键.
4.D
【分析】直接利用点的坐标,正确结合坐标系分析即可.
【详解】解:如图所示:有一直线通过点且与轴垂直,故也会通过点.
故选D.
【点睛】本题主要考查点的坐标,正确结合平面直角坐标系分析是解题关键.
5.B
【分析】根据点在x轴上的坐标特点解答即可.
【详解】选项A在轴上,故本选项不符合题意;
选项B 在轴上,故本选项符合题意;
选项C 在第一象限,故本选项不符合题意;
选项D在第三象限,故本选项不符合题意;
故选:.
【点睛】本题考查了点的坐标.解题的关键是明确在x轴上的点的坐标特点:纵坐标为0.
6.B
【分析】根据点到坐标轴的距离及点所在的象限解答即可.
【详解】解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x>0,y<0,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:B.
【点睛】此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
7.C
【分析】根据x轴、y轴上点、第一象限以及第二象限点得坐标特征即可解答.
【详解】解:A.当点A在x轴上时,,解得,错误;
B.当点A在y轴上时,,解得,错误;
C.当时,,所以点A在第一象限,正确;
D.当时,,所以点A在第三象限,错误.
故答案为C.
【点睛】本题主要考查了x轴、y轴上点、第一象限以及第二象限点得坐标特征,掌握直角坐标系内点得特征成为解答本题的关键.
8.C
【分析】根据平移变化与坐标变化规律:横坐标,右移加,左移减;纵坐标,上移加,下移减,即得答案.
【详解】∵“士”向左移动1个单位,向上移动1个单位到达“将”的位置,
∴“将”的位置的坐标为(-2-1,-1+1),即(-3,1).
故选:C.
【点睛】本题考查了坐标的平移,熟练掌握坐标平移的方法是解题的关键.
9.C
【分析】先根据A点所处象限及绝对值定义求出它的坐标,再根据平面直角坐标系内点的平移规律求解即可.
【详解】解:∵点在第四象限,
∴x>0,y<0,
∵,
∴x=2,y=-3,
∵将点A向左平移3个单位长度后得到点,
∴,
故选:C.
【点睛】本题考查了平面直角坐标系内点的坐标特点、点的平移规律等知识点,解题关键是掌握平移过程中点的坐标的变化规律:横坐标“左减右加”,纵坐标“上加下减”.
10.A
【分析】利用点的平移和点的坐标的变化规律进行计算即可.
【详解】解:点M(2,4)向下平移2个单位长度,得到的点的坐标是(2,4-2),
即(2,2),
故选:A.
【点睛】此题主要考查了坐标与图形的变化--平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
11.(7,0)
【分析】根据x轴上点的纵坐标为0列方程求出,再求解即可.
【详解】∵P点坐标为(4-a,3a+9),且点P在轴上,
∴,
解得,
,
所以,点P的坐标为(7,0).
故答案为:(7,0).
【点睛】本题考查了点的坐标,熟记轴上点的纵坐标为0是解题的关键.
12.(2021,0)
【分析】由图中点的坐标可得:每4次运动为一个循环组循环,并且每一个循环组向右运动4个单位,用2022除以4,再由商和余数的情况确定运动后点的坐标.
【详解】由图中点的坐标可得:每4次运动为一个循环组循环,并且每一个循环组向右运动4个单位,
∵2022÷4=505余2,
∴第2022次运动为第505循环组的第2次运动,
横坐标为,纵坐标为0,
∴点P运动第2022次的坐标为(2021,0).
故答案为:(2021,0).
【点睛】考查了点的坐标规律,解题关键是观察点的坐标变化,并寻找规律.
13.(-1,2)
【分析】先根据点A,点B的坐标建立直角坐标系,再确定点C的坐标即可.
【详解】根据点A(-2,0),点B(1,1),以点A所在的直线为x轴,点A右侧2个单位长度竖直方向为y轴建立直角坐标系,如图所示.
所以点C的坐标是(-1,2).
故答案为:(-1,2).
【点睛】本题主要考查了平面直角坐标系内点的坐标,建立适当的直角坐标系是解题的关键.
14.1
【分析】直接利用点在第一象限横纵坐标都大于0,再由到两坐标轴的距离相等得出等式求出答案.
【详解】解:在第一象限,且到两坐标轴的距离相等,
,
解得:.
故答案为:.
【点睛】本题主要考查了点到坐标轴的距离,根据到两坐标轴的距离相等列出方程是解题的关键.
15.
【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是2、0、-2、0、2、0、-2、…,四个一循环,继而求得答案.
【详解】解:观察图形可知, 点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)…的横坐标依次是1、2、3、4、…、n,
纵坐标依次是2、0、-2、0、2、0、-2、…,
四个一循环, 2022÷4=505…2,
故点A2022坐标是(2022,0).
故答案为:(2022,0).
【点睛】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解此题的关键是根据图形得出规律.
16.8
【分析】根据两点的纵坐标相同,因此线段轴,计算点的横坐标的差即可求出A,B两点间的距离.
【详解】解:∵A(﹣3,4),B(5,4),
∴轴,
∴,
故答案为:8.
【点睛】本题考查平面上两点之间的距离,根据两点的坐标的特点进行求解是解题的关键.
17.
【分析】先根据音乐台的坐标和牡丹园的坐标建立平面直角坐标系,再结合坐标系可得答案.
【详解】解:根据题意建立平面直角坐标系,如下图:
∴游乐园的坐标为.
故答案为:
【点睛】本题主要考查坐标确定位置,解题的关键是根据已知点的坐标建立平面直角坐标系.
18.(1)平行,(-2,-3)
(2)7,(5,-5)
(3)经过秒时,,两点的距离为
【分析】(1)由A,两点横坐标相同可判断轴,根据,从而求得点坐标;
(2)当时,之间的距离最小,进一步求得结果;
(3)当点,两点的纵坐标相同时,,进一步求得结果.
【详解】(1)解:,
,两点的横坐标相同,
轴,
轴轴,
轴,
,,,
,
,
点,
故答案为:平行,;
(2)当时,d最小,此时,
此时点的横坐标和点A的横坐标相同,纵坐标与点的纵坐标相同,
,
故答案为,;
(3)当,之间距离等于时,点和点的纵坐标相同,
,
,
经过秒时,,两点的距离为.
【点睛】本题考查了平面直角坐标系中点的坐标特点与线段的位置之间关系等知识,解决问题的关键是根据点的坐标来确定线段之间的关系.
19.(1)C
(2)①(0,3),(3,0);②或;③分类讨论(答案不唯一);
【分析】(1)根据数学的历史知识判断即可;
(2)分别作出点A、B、C平移后的坐标,再连接相应顶点;①根据坐标的定义写出坐标即可;②根据坐标特征可得的底边上的高为3,求得底边的长,再分别讨论点D在左边和右边即可;③根据②的解答方法判断即可;
【详解】(1)解:最早引入坐标系,用代数方法研究几何图形的数学家是:笛卡尔;
故选: C.
(2)解:如图,点A、B、C分别向下平移1个单位长度,再向右平移2个单位长度得到点A1、B1、C1,连接相应顶点则即为所求;
①由图象可得的坐标,的坐标;
故答案为:(0,3),(3,0);
② ∵D点在x轴上,的面积等于3,的坐标,
∴底边上的高为3,
∴的长度为2,
∵的坐标,
∴当点D在左边时,D点坐标为(1,0),当点D在右边时,D点坐标为(5,0);
③∵根据点D在点左边和右边分别讨论,
∴利用了分类讨论的思想;
故答案为:分类讨论(答案不唯一).
【点睛】本题考查了平面直角坐标系,坐标的定义,坐标的规律等知识;根据D点位置分类讨论是解题关键.
20.(1)-2,0;(2)存在,(0,6)或(0,-6);(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM,证明见解析
【分析】(1)根据坐标轴上,两点间的距离的计算方法,即可得出结论;
(2)先求出△ABC的面积,进而求出△BOP的面积,最后用三角形的面积公式,建立方程,求解,即可得出结论;
(3)先判断出BH∥x轴,再分两种情况,利用平行线的性质和三角形的外角的性质,即得出结论.
【详解】解:(1),,
,
故答案为:-2,0;
(2)如图1,,,
,
,
,
设,
,
,
,
或;
(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM.
证明:由平移知,H(-2,3),
∵B(2,3),
∴BH∥x轴,
①当点M在线段CH上时,如图2,
过点M作MG∥x轴,
∴∠AMG=∠MAC,
∵BH∥x轴,MG∥x轴,
∴BH∥MG,
∴∠BMG=∠HBM,
∴∠BMA=∠AMG+∠BMG=∠MAC+∠MBH;
②当点M在CH的延长线上时,如图3,
记AM与BH的交点为N,
∵BH∥x轴,
∴∠MNH=∠MAC,
∵∠MNH是△BMN的外角,
∴∠MNH=∠BMA+∠HBM,
∴∠MAC=∠BMA+∠HBM,
即∠BMA=∠MAC+∠MAC或∠MAC=∠BMA+∠HBM.
【点睛】此题是几何变换综合题,主要考查了平移的性质,三角形的面积公式,平行线的性质,三角形的外角的性质,作出辅助线是解本题的关键.
21.(1)见解析;(2)见解析;(3)的坐标为.
【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)利用A点坐标画出直角坐标系;
(3)利用第二象限点的坐标特征写出点A1的坐标.
【详解】解:(1)如图,为所作;
(2)如上图所示;
(3)点的坐标为.
【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
22.(1)建立平面直角坐标系见解析;C(2,4);
(2)作图见解析
(3)12.5
【分析】(1)根据A,B两点坐标,画出平面直角坐标系即可;
(2)利用平移变换的性质分别作出A,B, C的对应点D,E, F即可;
(3)把四边形面积看成矩形面积减去周围特殊图形的面积即可.
【详解】(1)平面直角坐标系如图所示:
C(2,4);
(2)如图, DEF即为所求,
F(0,3);
(3)四边形DBCF的面积,
故答案为:12.5.
【点睛】本题考查作图-平移变换,求四边形的面积等知识,解题的关键是掌握平移变换的性质,学会利用割补法求四边形面积.
23.(1)
(2)见解析,
【分析】(1)根据点的坐标的表示方法写出A、B点的坐标;
(2)利用点平移的坐标变换规律写出A′、B′、C′的坐标,然后描点即可得到三角形三角形A'B'C'.
(1)
解:根据图可知A点的坐标、B点的坐标 ;
故答案为:(2,﹣1),(4,3)
(2)
解:如图,三角形即为所求,
从图中可知、、.
【点睛】本题考查了作图﹣平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
24.(1)或
(2),理由见解析
【分析】(1)根据平移的性质求出点C的坐标,然后根据的面积是的面积的2倍列式求出OP,即可得到点P的坐标;
(2)过点D作,根据平移的性质和平行线的性质求出,,作差即可得出结论.
(1)
解:∵线段平移至线段的位置,点A的坐标是,点B的坐标是,
∴点C的坐标是,
如图,过点C作轴于点H,轴于点F.
∴.
∵点B的坐标为,
∴,
∵的面积是的面积的2倍,
∴,即,
∴.
∴点P的坐标是或;
(2)
.
理由:如图,过点D作.
∴,
由平移得:,
∴,
∴,
∴,
∵,
∴.
【点睛】本题主要考查了平移的性质,平行线的性质,坐标与图形性质,熟练掌握平移的性质是解题的关键.
25.(1)B(3,0),图见解析
(2)图见解析,,,
【分析】(1)先根据三角形ABC的面积求出AB的长,再根据A点坐标结合B在x正半轴上求出B点坐标,然后顺次连接A、B、C即可;
(2)先根据平移方式求出A、B、C对应点的坐标,然后画出平移后的图形即可.
(1)
解:∵△ABC的面积为10,
∴,
∴AB=5,
∵A(-2,0),点B在轴的正半轴上,
∴B(3,0),
如图所示△ABC为所求的图形;
(2)
解:如图为所求的图形;
∵将△ABC先向右平移3个单位长度,再向下平移5个单位长度得到,A(-2,0),B(3,0),C(1,4),
∴,,.
【点睛】本题主要考查了坐标与图形,画平移图形,熟知相关知识是解题的关键.
26.(1)见解析
(2)5
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点,,即可;
(2)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(1)
如图,三角形'即为所求;
(2)
三角形的面积=3×42×22×31×4=5.
故答案为:5.
【点睛】本题考查作图﹣平移变换,三角形的面积等知识,解题的关键是掌握平移变换的性质,学会用割补法求三角形面积.
一、单选题
1.(2022春·山西忻州·七年级统考期末)家长会前,四个孩子分别向家长描述自己在班里的座位,家长能准确找到自己孩子座位的是( )
A.小明说他坐在第1排 B.小白说他坐在第3列 C.小清说她坐在第2排第5列 D.小楚说他的座位靠窗
2.(2022春·山西忻州·七年级统考期末)已知A点的坐标为(3,a+3),B点的坐标为(a,4),AB∥x轴,则线段AB的长为( )
A.5 B.4 C.3 D.2
3.(2022春·山西吕梁·七年级统考期末)若点A(,)在第二、四象限的平分线上,则点A的坐标为( )
A.(5,-5) B.(-5,-5) C.(5,5) D.(-5,5)
4.(2022春·山西朔州·七年级统考期末)如图的坐标平面上有原点与、、、四点.若有一直线通过点且与轴垂直,则也会通过下列哪一点?( )
A. B. C. D.
5.(2022春·山西临汾·七年级统考期末)下列四个点中,在平面直角坐标系内位于轴上的点是( )
A.(0,2022) B.(2022,0) C.(2022,2) D.(-2,-2022)
6.(2022春·山西临汾·七年级统考期末)在平面直角坐标系的第四象限内有一点,到轴的距离为4,到轴的距离为5,则点的坐标为( )
A. B. C. D.
7.(2022春·山西大同·七年级统考期末)在平面直角坐标系中,点A的坐标是(3a﹣9,a﹣2),则下列说法正确的是( )
A.当点A在x轴上时,a=3 B.当点A在y轴上时,a=2
C.当a>3时,点A在第一象限 D.当a<2时,点A在第二象限
8.(2022春·山西吕梁·七年级统考期末)中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用表示“炮”的位置,表示“士”的位置,那么“将”的位置应表示为( )
A. B. C. D.
9.(2022春·山西吕梁·七年级统考期末)在平面直角坐标系中,点在第四象限,且,将点A向左平移3个单位长度后得到点,则点的坐标是( )
A. B. C. D.
10.(2022春·山西忻州·七年级统考期末)点向下平移2个单位长度,得到的点的坐标是( )
A. B. C. D.
二、填空题
11.(2022春·山西忻州·七年级统考期末)已知P点坐标为(4-a,3a+9),且点P在轴上,则点P的坐标是______.
12.(2022春·山西忻州·七年级统考期末)如图,直角坐标平面xoy内,动点P按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),…按这样的运动规律,动点P第2022次运动到点的坐标是_____.
13.(2022春·山西吕梁·七年级统考期末)如图是一足球场的半场平面示意图,已知球员A的位置为(-2,0),球员B的位置为(1,1),则球员C的位置为________.
14.(2022春·山西临汾·七年级统考期末)已知点在第一象限,且到两坐标轴距离相等,则的值是______.
15.(2022春·山西吕梁·七年级统考期末)如图,点,,,,…….根据这个规律,探究可得点的坐标是_________.
16.(2022春·山西大同·七年级统考期末)已知点A(﹣3,4),B(5,4),则A,B两点间的距离是____________.
17.(2022春·山西吕梁·七年级统考期末)如图是某公园的平面示意图的一部分.在此图中,若音乐台的坐标为,牡丹园的坐标为.则游乐园的坐标为_________.
三、解答题
18.(2022春·山西临汾·七年级统考期末)如图,四边形放置在平面直角坐标系中,,,点,,的坐标分别为(5,8),(5,0),(-2,5).
(1)与轴的位置关系是______(填“平行”或“相交”),点的坐标为______;
(2)是线段上一动点,则距离的最小值______,距离最小时,点的坐标是______;
(3),分别是线段,上的动点,从出发向点运动,速度为每秒个单位长度,从出发向点运动,速度为每秒个单位长度,若两点同时出发,几秒后、两点距离恰好为?
19.(2022春·山西吕梁·七年级统考期末)平面直角坐标系是由原点重合且互相垂直的两条数轴构成的,它是沟通代数与几何的桥梁,是非常重要的数学工具.
(1)最早引入坐标系,用代数方法研究几何图形的数学家是( )
A.祖冲之 B.刘徽 C.笛卡尔 D.欧几里得
(2)在数学活动课上,老师与同学们一起探究如下问题:
在平面直角坐标系中的位置如图,已知点的坐标为.把向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的.
①写出点的坐标_________,的坐标_________;
②在轴上找一点,使的面积等于3,求满足条件的点的坐标;
③在解决问题②时用到的数学思想是__________________(填一个即可)
20.(2022春·山西忻州·七年级统考期末)如图,在平面直角坐标系中,已知△ABC中,点A坐标为(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)写出点C的坐标( , )
(2)在y轴上是否存在点P,使得S△POB=S△ABC,若存在,求出点P的坐标;若不存在;
(3)把点C往上平移3个单位得到点H,画射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探索∠BMA、∠HBM、∠MAC之间的数量关系,并证明你的结论.
21.(2022春·山西朔州·七年级统考期末)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,的三个顶点均在格点上.
(1)将先向右平移6个单位长度,再向上平移3个单位长度,得到,画出平移后的;
(2)建立适当的平面直角坐标系,使得点的坐为;
(3)在(2)的条件下,直接写出点的坐标.
22.(2022春·山西朔州·七年级统考期末)如图是由边长为1的小正方形组成的网格,每个小正方形的顶点叫做格点,点A,B,C均在格点上.若点A,B的坐标分别为(1,1),B(4,0),请解答下列问题:
(1)请建立平面直角坐标系,并直接写出点C的坐标;
(2)将△ABC先向左平移2个单位长度,再向下平移1个单位长度得到△DEF,(点A,B,C的对应点分别为D,E,F),画出△DEF,并直接写出点F的坐标;
(3)直接写出(2)中四边形DBCF的面积为________.
23.(2022春·山西大同·七年级统考期末)如图,在平面直角坐标系中,三角形ABC的三个顶点都在网格的格点上,其中点C的坐标为(1,2).
(1)点A的坐标为____________,点B的坐标为____________;
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',请画出平移后的三角形A'B'C',并写出点A',B',C'的坐标.
24.(2022春·山西大同·七年级统考期末)综合与探究
在平面直角坐标系中,点A在第四象限,将线段AO平移至线段BC的位置,点A的对应点是点B,点O的对应点是点C.
(1)如图①,点A的坐标是(2,﹣3),点B的坐标是(﹣3,0),连接OC.若在y轴上存在一点P,使得三角形COP的面积是三角形OBC的面积的2倍,求点P的坐标.
(2)如图②,当点C在y轴的正半轴上,点D在y轴的负半轴上,且∠ADB=90°时,试猜想∠CBD与∠OAD的数量关系,并说明理由.
25.(2022春·山西吕梁·七年级统考期末)如图,已知A(-2,0),C(1,4),点B在轴的正半轴上,已知△ABC的面积为10.
(1)求点B的坐标,并画出△ABC;
(2)将△ABC先向右平移3个单位长度,再向下平移5个单位长度,画出平移后的,并写出,,的坐标.
26.(2022春·山西吕梁·七年级统考期末)如图,平面直角坐标中,三角形的三个顶点坐标分别为,,.
(1)将三角形先向右平移4个单位,再向下平移2个单位,在平面直角坐标系中画出平移后的三角形;
(2)直接写出三角形的面积为_________.
参考答案:
1.C
【分析】直接利用坐标确定位置需要两个量,进而分析得出答案.
【详解】解:A.小明说他坐在第1排,无法确定座位位置,故此选项不合题意;
B.小白说他坐在第3列,无法确定座位位置,故此选项不合题意;
C.小清说她坐在第2排第5列,可以确定座位位置,故此选项符合题意;
D.小楚说他的座位靠窗,无法确定座位位置,故此选项不合题意;
故选:C.
【点睛】本题主要考查了坐标确定位置,掌握具体位置确定需两个量是解题关键.
2.D
【分析】先根据轴,求出a的值,再求出AB的长即可.
【详解】∵轴,
∴a+3=4,
解得a=1.
∴点A(3,4),点B(1,4),
∴AB=3-1=2.
故选:D.
【点睛】本题主要考查了平面直角坐标系内点的特征,根据轴求出a值是解题的关键.
3.A
【分析】根据二、四象限角平分线上的点横坐标与纵坐标互为相反数列得关于m的方程求得m的值,进而确定A的坐标.
【详解】解:∵A(3+m,m-7)在第二、四象限的平分线上,
∴(3+m)+(m-7)=0,解得m=2,
∴3+m=5,m-7=-5,
∴A的坐标为(5,-5).
故选:A.
【点睛】本题主要考查了点的坐标、解一元一次方程等知识点,根据二、四象限角平分线上的点横坐标与纵坐标互为相反数列出关于m的方程是解本答题的关键.
4.D
【分析】直接利用点的坐标,正确结合坐标系分析即可.
【详解】解:如图所示:有一直线通过点且与轴垂直,故也会通过点.
故选D.
【点睛】本题主要考查点的坐标,正确结合平面直角坐标系分析是解题关键.
5.B
【分析】根据点在x轴上的坐标特点解答即可.
【详解】选项A在轴上,故本选项不符合题意;
选项B 在轴上,故本选项符合题意;
选项C 在第一象限,故本选项不符合题意;
选项D在第三象限,故本选项不符合题意;
故选:.
【点睛】本题考查了点的坐标.解题的关键是明确在x轴上的点的坐标特点:纵坐标为0.
6.B
【分析】根据点到坐标轴的距离及点所在的象限解答即可.
【详解】解:设点M的坐标为(x,y),
∵点M到x轴的距离为4,
∴,
∴,
∵点M到y轴的距离为5,
∴,
∴,
∵点M在第四象限内,
∴x>0,y<0,
∴x=5,y=-4,
即点M的坐标为(5,-4).
故选:B.
【点睛】此题考查平面直角坐标系中的点到坐标轴的距离,象限内点的坐标的符号特点等,其中要牢记第四象限内的点的坐标符号特点为(+,-).
7.C
【分析】根据x轴、y轴上点、第一象限以及第二象限点得坐标特征即可解答.
【详解】解:A.当点A在x轴上时,,解得,错误;
B.当点A在y轴上时,,解得,错误;
C.当时,,所以点A在第一象限,正确;
D.当时,,所以点A在第三象限,错误.
故答案为C.
【点睛】本题主要考查了x轴、y轴上点、第一象限以及第二象限点得坐标特征,掌握直角坐标系内点得特征成为解答本题的关键.
8.C
【分析】根据平移变化与坐标变化规律:横坐标,右移加,左移减;纵坐标,上移加,下移减,即得答案.
【详解】∵“士”向左移动1个单位,向上移动1个单位到达“将”的位置,
∴“将”的位置的坐标为(-2-1,-1+1),即(-3,1).
故选:C.
【点睛】本题考查了坐标的平移,熟练掌握坐标平移的方法是解题的关键.
9.C
【分析】先根据A点所处象限及绝对值定义求出它的坐标,再根据平面直角坐标系内点的平移规律求解即可.
【详解】解:∵点在第四象限,
∴x>0,y<0,
∵,
∴x=2,y=-3,
∵将点A向左平移3个单位长度后得到点,
∴,
故选:C.
【点睛】本题考查了平面直角坐标系内点的坐标特点、点的平移规律等知识点,解题关键是掌握平移过程中点的坐标的变化规律:横坐标“左减右加”,纵坐标“上加下减”.
10.A
【分析】利用点的平移和点的坐标的变化规律进行计算即可.
【详解】解:点M(2,4)向下平移2个单位长度,得到的点的坐标是(2,4-2),
即(2,2),
故选:A.
【点睛】此题主要考查了坐标与图形的变化--平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
11.(7,0)
【分析】根据x轴上点的纵坐标为0列方程求出,再求解即可.
【详解】∵P点坐标为(4-a,3a+9),且点P在轴上,
∴,
解得,
,
所以,点P的坐标为(7,0).
故答案为:(7,0).
【点睛】本题考查了点的坐标,熟记轴上点的纵坐标为0是解题的关键.
12.(2021,0)
【分析】由图中点的坐标可得:每4次运动为一个循环组循环,并且每一个循环组向右运动4个单位,用2022除以4,再由商和余数的情况确定运动后点的坐标.
【详解】由图中点的坐标可得:每4次运动为一个循环组循环,并且每一个循环组向右运动4个单位,
∵2022÷4=505余2,
∴第2022次运动为第505循环组的第2次运动,
横坐标为,纵坐标为0,
∴点P运动第2022次的坐标为(2021,0).
故答案为:(2021,0).
【点睛】考查了点的坐标规律,解题关键是观察点的坐标变化,并寻找规律.
13.(-1,2)
【分析】先根据点A,点B的坐标建立直角坐标系,再确定点C的坐标即可.
【详解】根据点A(-2,0),点B(1,1),以点A所在的直线为x轴,点A右侧2个单位长度竖直方向为y轴建立直角坐标系,如图所示.
所以点C的坐标是(-1,2).
故答案为:(-1,2).
【点睛】本题主要考查了平面直角坐标系内点的坐标,建立适当的直角坐标系是解题的关键.
14.1
【分析】直接利用点在第一象限横纵坐标都大于0,再由到两坐标轴的距离相等得出等式求出答案.
【详解】解:在第一象限,且到两坐标轴的距离相等,
,
解得:.
故答案为:.
【点睛】本题主要考查了点到坐标轴的距离,根据到两坐标轴的距离相等列出方程是解题的关键.
15.
【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是2、0、-2、0、2、0、-2、…,四个一循环,继而求得答案.
【详解】解:观察图形可知, 点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)…的横坐标依次是1、2、3、4、…、n,
纵坐标依次是2、0、-2、0、2、0、-2、…,
四个一循环, 2022÷4=505…2,
故点A2022坐标是(2022,0).
故答案为:(2022,0).
【点睛】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解此题的关键是根据图形得出规律.
16.8
【分析】根据两点的纵坐标相同,因此线段轴,计算点的横坐标的差即可求出A,B两点间的距离.
【详解】解:∵A(﹣3,4),B(5,4),
∴轴,
∴,
故答案为:8.
【点睛】本题考查平面上两点之间的距离,根据两点的坐标的特点进行求解是解题的关键.
17.
【分析】先根据音乐台的坐标和牡丹园的坐标建立平面直角坐标系,再结合坐标系可得答案.
【详解】解:根据题意建立平面直角坐标系,如下图:
∴游乐园的坐标为.
故答案为:
【点睛】本题主要考查坐标确定位置,解题的关键是根据已知点的坐标建立平面直角坐标系.
18.(1)平行,(-2,-3)
(2)7,(5,-5)
(3)经过秒时,,两点的距离为
【分析】(1)由A,两点横坐标相同可判断轴,根据,从而求得点坐标;
(2)当时,之间的距离最小,进一步求得结果;
(3)当点,两点的纵坐标相同时,,进一步求得结果.
【详解】(1)解:,
,两点的横坐标相同,
轴,
轴轴,
轴,
,,,
,
,
点,
故答案为:平行,;
(2)当时,d最小,此时,
此时点的横坐标和点A的横坐标相同,纵坐标与点的纵坐标相同,
,
故答案为,;
(3)当,之间距离等于时,点和点的纵坐标相同,
,
,
经过秒时,,两点的距离为.
【点睛】本题考查了平面直角坐标系中点的坐标特点与线段的位置之间关系等知识,解决问题的关键是根据点的坐标来确定线段之间的关系.
19.(1)C
(2)①(0,3),(3,0);②或;③分类讨论(答案不唯一);
【分析】(1)根据数学的历史知识判断即可;
(2)分别作出点A、B、C平移后的坐标,再连接相应顶点;①根据坐标的定义写出坐标即可;②根据坐标特征可得的底边上的高为3,求得底边的长,再分别讨论点D在左边和右边即可;③根据②的解答方法判断即可;
【详解】(1)解:最早引入坐标系,用代数方法研究几何图形的数学家是:笛卡尔;
故选: C.
(2)解:如图,点A、B、C分别向下平移1个单位长度,再向右平移2个单位长度得到点A1、B1、C1,连接相应顶点则即为所求;
①由图象可得的坐标,的坐标;
故答案为:(0,3),(3,0);
② ∵D点在x轴上,的面积等于3,的坐标,
∴底边上的高为3,
∴的长度为2,
∵的坐标,
∴当点D在左边时,D点坐标为(1,0),当点D在右边时,D点坐标为(5,0);
③∵根据点D在点左边和右边分别讨论,
∴利用了分类讨论的思想;
故答案为:分类讨论(答案不唯一).
【点睛】本题考查了平面直角坐标系,坐标的定义,坐标的规律等知识;根据D点位置分类讨论是解题关键.
20.(1)-2,0;(2)存在,(0,6)或(0,-6);(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM,证明见解析
【分析】(1)根据坐标轴上,两点间的距离的计算方法,即可得出结论;
(2)先求出△ABC的面积,进而求出△BOP的面积,最后用三角形的面积公式,建立方程,求解,即可得出结论;
(3)先判断出BH∥x轴,再分两种情况,利用平行线的性质和三角形的外角的性质,即得出结论.
【详解】解:(1),,
,
故答案为:-2,0;
(2)如图1,,,
,
,
,
设,
,
,
,
或;
(3)∠BMA=∠MAC+∠MBH或∠MAC=∠BMA+∠HBM.
证明:由平移知,H(-2,3),
∵B(2,3),
∴BH∥x轴,
①当点M在线段CH上时,如图2,
过点M作MG∥x轴,
∴∠AMG=∠MAC,
∵BH∥x轴,MG∥x轴,
∴BH∥MG,
∴∠BMG=∠HBM,
∴∠BMA=∠AMG+∠BMG=∠MAC+∠MBH;
②当点M在CH的延长线上时,如图3,
记AM与BH的交点为N,
∵BH∥x轴,
∴∠MNH=∠MAC,
∵∠MNH是△BMN的外角,
∴∠MNH=∠BMA+∠HBM,
∴∠MAC=∠BMA+∠HBM,
即∠BMA=∠MAC+∠MAC或∠MAC=∠BMA+∠HBM.
【点睛】此题是几何变换综合题,主要考查了平移的性质,三角形的面积公式,平行线的性质,三角形的外角的性质,作出辅助线是解本题的关键.
21.(1)见解析;(2)见解析;(3)的坐标为.
【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)利用A点坐标画出直角坐标系;
(3)利用第二象限点的坐标特征写出点A1的坐标.
【详解】解:(1)如图,为所作;
(2)如上图所示;
(3)点的坐标为.
【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
22.(1)建立平面直角坐标系见解析;C(2,4);
(2)作图见解析
(3)12.5
【分析】(1)根据A,B两点坐标,画出平面直角坐标系即可;
(2)利用平移变换的性质分别作出A,B, C的对应点D,E, F即可;
(3)把四边形面积看成矩形面积减去周围特殊图形的面积即可.
【详解】(1)平面直角坐标系如图所示:
C(2,4);
(2)如图, DEF即为所求,
F(0,3);
(3)四边形DBCF的面积,
故答案为:12.5.
【点睛】本题考查作图-平移变换,求四边形的面积等知识,解题的关键是掌握平移变换的性质,学会利用割补法求四边形面积.
23.(1)
(2)见解析,
【分析】(1)根据点的坐标的表示方法写出A、B点的坐标;
(2)利用点平移的坐标变换规律写出A′、B′、C′的坐标,然后描点即可得到三角形三角形A'B'C'.
(1)
解:根据图可知A点的坐标、B点的坐标 ;
故答案为:(2,﹣1),(4,3)
(2)
解:如图,三角形即为所求,
从图中可知、、.
【点睛】本题考查了作图﹣平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
24.(1)或
(2),理由见解析
【分析】(1)根据平移的性质求出点C的坐标,然后根据的面积是的面积的2倍列式求出OP,即可得到点P的坐标;
(2)过点D作,根据平移的性质和平行线的性质求出,,作差即可得出结论.
(1)
解:∵线段平移至线段的位置,点A的坐标是,点B的坐标是,
∴点C的坐标是,
如图,过点C作轴于点H,轴于点F.
∴.
∵点B的坐标为,
∴,
∵的面积是的面积的2倍,
∴,即,
∴.
∴点P的坐标是或;
(2)
.
理由:如图,过点D作.
∴,
由平移得:,
∴,
∴,
∴,
∵,
∴.
【点睛】本题主要考查了平移的性质,平行线的性质,坐标与图形性质,熟练掌握平移的性质是解题的关键.
25.(1)B(3,0),图见解析
(2)图见解析,,,
【分析】(1)先根据三角形ABC的面积求出AB的长,再根据A点坐标结合B在x正半轴上求出B点坐标,然后顺次连接A、B、C即可;
(2)先根据平移方式求出A、B、C对应点的坐标,然后画出平移后的图形即可.
(1)
解:∵△ABC的面积为10,
∴,
∴AB=5,
∵A(-2,0),点B在轴的正半轴上,
∴B(3,0),
如图所示△ABC为所求的图形;
(2)
解:如图为所求的图形;
∵将△ABC先向右平移3个单位长度,再向下平移5个单位长度得到,A(-2,0),B(3,0),C(1,4),
∴,,.
【点睛】本题主要考查了坐标与图形,画平移图形,熟知相关知识是解题的关键.
26.(1)见解析
(2)5
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点,,即可;
(2)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可.
(1)
如图,三角形'即为所求;
(2)
三角形的面积=3×42×22×31×4=5.
故答案为:5.
【点睛】本题考查作图﹣平移变换,三角形的面积等知识,解题的关键是掌握平移变换的性质,学会用割补法求三角形面积.
