直线与圆的位置关系[下学期]
文档属性
| 名称 | 直线与圆的位置关系[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 465.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-10-16 09:28:00 | ||
图片预览



文档简介
课件21张PPT。6.2 直线与圆的位置关系
临海中学 赵玲琴圣诞节快乐学习目标能利用d 与 r的大小关系判断直线与圆的位置关系;
能利用直线与圆的位置关系得到d 与 r的大小关系;
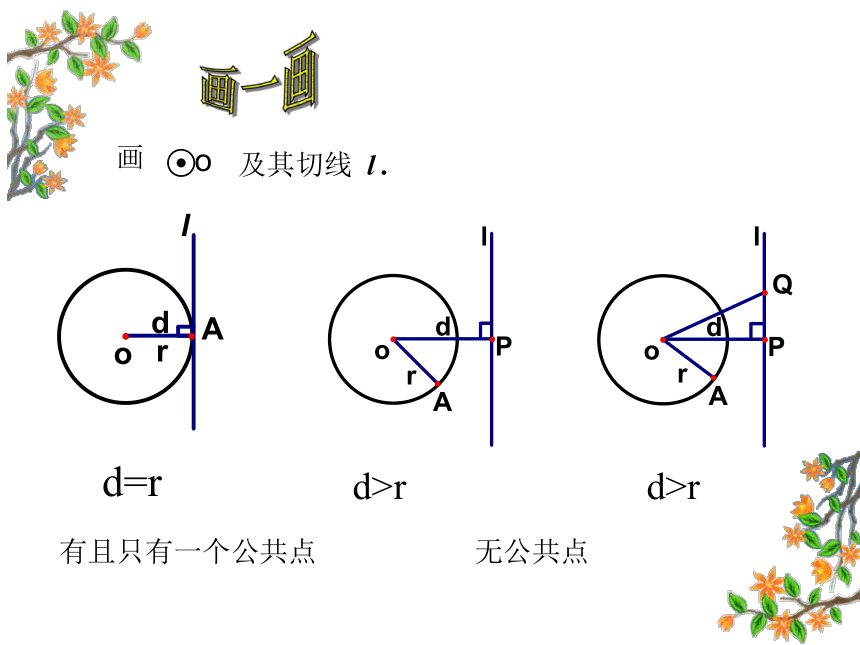
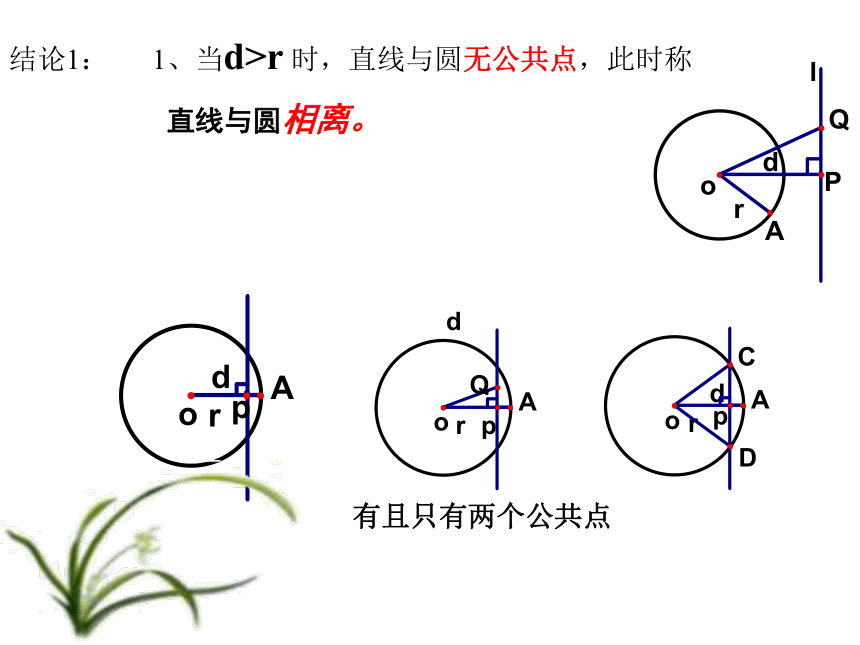
能进一步利用d=r证明直线是圆的切线.画一画 画及其切线 l . 有且只有一个公共点 d=rd>rd>r无公共点 有两个公共点结论1: 1、当d>r 时,直线与圆无公共点,此时称
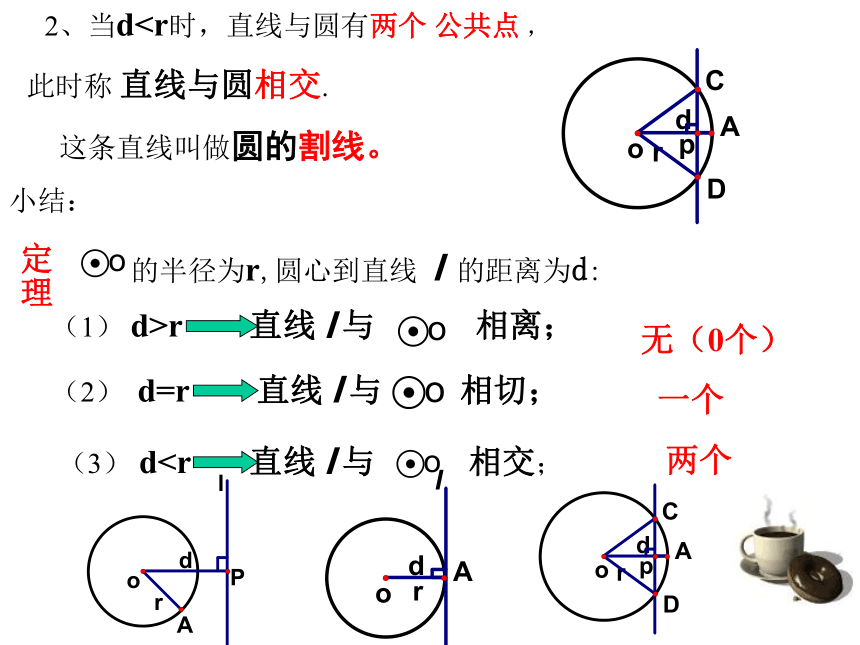
直线与圆相离。有且只有两个公共点 2、当d此时称 直线与圆相交. 这条直线叫做圆的割线。小结: 的半径为r,圆心到直线 l 的距离为d:
(1) d>r 直线 与 相离; 无(0个)
一个
两个
(2) d=r 直线 与相切;(3) d =2 , = ; ( )
13 = 12 ; ( )
= , = ; ( )dddddrrrrr 相切 相离 相交 相离看谁答得对?试一试反过来,(1) 直线 与 相离 d>r (2) 直线 与 相切 d=r (3) 直线 与 相交 dr 直线 与 相离(2) d=r 直线 与 相切(3) d(1) 2cm,(2)3cm, (3) 6cm,那么直线与圆的
位置关系分别为:
(1) 2cm ( )
(2) 3cm ( )
(3) 6cm ( ) 相交 相切 相离 3.已知 的半径 r=3cm ,当直线与圆心的距离 d 取什么范围?有
(1)相离 (2) 相切 (3) 相交 d=3
d>3看谁答得快?0 d<3比一比4. 在ΔABC中,AB=5cm,BC=4cm,AC=3cm.(1) 以C为圆心,2cm长为半径画 ,则 与AB-----相离 (2) 以C为圆心,画 与AB相切,此时 的半径是---2.4cm (3) 以A为圆心, 3cm长为半径画 ,此时 的切线是---切点是--直线BC 点C看谁画得好比一比5. 已知 的半径 r=7cm ,直线 ,且 与
相切,圆心O到 的距离为9cm,求 和 的距离。 解:分两种情况。
(1)当 , 在圆心同侧时,
和 的距离= 9 –7=2 (cm) (2) 当 , 在圆心两侧时,
和 的距离=9+7 =16cm答: 和 的距离是2cm或16cm。 则直线a, 直线b都是所求作的直线。6、已知 和直线 ,作直线 与 相切,并使 例 如图,点P为 的角平分线上的一点, 与BC相切.
求证: 与AB相切。(1) 证明切线有哪几种方法?分析: (2) 本题具备了哪个条件? (3) 应选择哪种方法? (4)怎样证明?证明:设 的半径为 r ,点P到BC,AB的距离分别为 , .点P在 的角平分线上 与BC相切rr与直线相切.1 有公共点,连接;
2 无公共点,作垂线段。无公共点方法2作垂线段证一证如图,AB,AC是两个同心圆中大圆的弦,AB=AC,且AB为小圆的切线, 求证: AC与小圆相切.证明: 设小圆的半径为 r,点o到AB,AC 的距离 分别为 , . 是AB的弦心距
是AC的弦心距 AB=AC AB是小圆的切线 rrAC与小圆相切1证一证2、如图,分别过 的直径AB的两个端点作直线CD的垂线,且AC+BD=AB.
求证:CD是 的切线。证明: 过O作OP CD于点P. AC CD
BD CD
OP CD O为AB 的中点OP是梯形ABDC的中位线AC+BD=2OPAC+BD=ABAB=2OPAB是直径OP是半径CD是 的切线小结: 1、
d与r关系 线与园关系 交点 直线名称 图形
d>r 相离 无 无
d=r 相切 一个 切线
d 2、能利用d=r 证明一条直线是园的切线。小结:同学们再见7、如图,已知点O和直线 l,以点O为圆心作一个圆和直线 l 相切。 拓广:已知直线 l 和直线上的点P,求作一个圆和直线相切于P.
临海中学 赵玲琴圣诞节快乐学习目标能利用d 与 r的大小关系判断直线与圆的位置关系;
能利用直线与圆的位置关系得到d 与 r的大小关系;
能进一步利用d=r证明直线是圆的切线.画一画 画及其切线 l . 有且只有一个公共点 d=rd>rd>r无公共点 有两个公共点结论1: 1、当d>r 时,直线与圆无公共点,此时称
直线与圆相离。有且只有两个公共点 2、当d
(1) d>r 直线 与 相离; 无(0个)
一个
两个
(2) d=r 直线 与相切;(3) d
13 = 12 ; ( )
= , = ; ( )dddddrrrrr 相切 相离 相交 相离看谁答得对?试一试反过来,(1) 直线 与 相离 d>r (2) 直线 与 相切 d=r (3) 直线 与 相交 d
位置关系分别为:
(1) 2cm ( )
(2) 3cm ( )
(3) 6cm ( ) 相交 相切 相离 3.已知 的半径 r=3cm ,当直线与圆心的距离 d 取什么范围?有
(1)相离 (2) 相切 (3) 相交 d=3
d>3看谁答得快?0 d<3比一比4. 在ΔABC中,AB=5cm,BC=4cm,AC=3cm.(1) 以C为圆心,2cm长为半径画 ,则 与AB-----相离 (2) 以C为圆心,画 与AB相切,此时 的半径是---2.4cm (3) 以A为圆心, 3cm长为半径画 ,此时 的切线是---切点是--直线BC 点C看谁画得好比一比5. 已知 的半径 r=7cm ,直线 ,且 与
相切,圆心O到 的距离为9cm,求 和 的距离。 解:分两种情况。
(1)当 , 在圆心同侧时,
和 的距离= 9 –7=2 (cm) (2) 当 , 在圆心两侧时,
和 的距离=9+7 =16cm答: 和 的距离是2cm或16cm。 则直线a, 直线b都是所求作的直线。6、已知 和直线 ,作直线 与 相切,并使 例 如图,点P为 的角平分线上的一点, 与BC相切.
求证: 与AB相切。(1) 证明切线有哪几种方法?分析: (2) 本题具备了哪个条件? (3) 应选择哪种方法? (4)怎样证明?证明:设 的半径为 r ,点P到BC,AB的距离分别为 , .点P在 的角平分线上 与BC相切rr与直线相切.1 有公共点,连接;
2 无公共点,作垂线段。无公共点方法2作垂线段证一证如图,AB,AC是两个同心圆中大圆的弦,AB=AC,且AB为小圆的切线, 求证: AC与小圆相切.证明: 设小圆的半径为 r,点o到AB,AC 的距离 分别为 , . 是AB的弦心距
是AC的弦心距 AB=AC AB是小圆的切线 rrAC与小圆相切1证一证2、如图,分别过 的直径AB的两个端点作直线CD的垂线,且AC+BD=AB.
求证:CD是 的切线。证明: 过O作OP CD于点P. AC CD
BD CD
OP CD O为AB 的中点OP是梯形ABDC的中位线AC+BD=2OPAC+BD=ABAB=2OPAB是直径OP是半径CD是 的切线小结: 1、
d与r关系 线与园关系 交点 直线名称 图形
d>r 相离 无 无
d=r 相切 一个 切线
d
同课章节目录
