2022-2023学年人教版数学八年级下册 19.1.1变量与函数强化训练卷(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级下册 19.1.1变量与函数强化训练卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览




文档简介
19.1.1变量与函数 强化训练卷
一、单选题
1.函数中自变量x的取值范围是( )
A. B. C. D.
2.如图,下列各曲线中,能够表示y是x的函数的是( )
A.(1)(2) B.(1)(4) C.(1)(2)(4) D.(1)(2)(3)(4)
3.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量
A.1个 B.2个 C.3个 D.4个
4.某水果销售商有100千克苹果,当苹果单价为15元/千克时,能全部销售完,市场调查表明苹果单价每提高1元,销售量减少6千克,若苹果单价提高x元,则苹果销售额y关于x的函数表达式为( )
A. B.
C. D.
5.下列各式中,表示y是x的函数的有( )
①2y+x=3;②y=x+2z;③y=2;④y=kx+1(k为常量);⑤y2=2x.
A.0个 B.1个 C.2个 D.3个
6.下列四个点中,在函数y=3x+1的图像上的是( )
A.(-1,2) B.(0,-1) C.(1,4) D.(2,-7)
7.在三角形面积公式S=ah,a=2cm中,下列说法正确的是( )
A.S,a是变量,h是常量 B.S,h是变量,是常量
C.S,h是变量,a是常量 D.S,h,a是变量,是常量
8.某学校用100元钱买乒乓球,所购买球的个数w与单价n(元)之间的关系是w=,其中( )
A.100是常量,w,n是变量
B.100,w是常量,n是变量
C.100,n是常量,w是变量
D.无法确定哪个是常量,哪个是变量
9.三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处点O与点P不重合利用仪器测量了的大小设蜜蜂飞行时间为的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.如果f(x)=3x-1,那么f(2)=_____________.
12.函数y=中,自变量x的取值范围是_____.
13.根据表格中的数据规律,当x=-4时,y的值是________.
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为______.
15.方程的解有________个.
三、解答题
16.已知等腰三角形的周长为cm,底边长为cm,一腰长为cm.
(1)求与之间的函数关系式;
(2)指出其中的变量和常量.
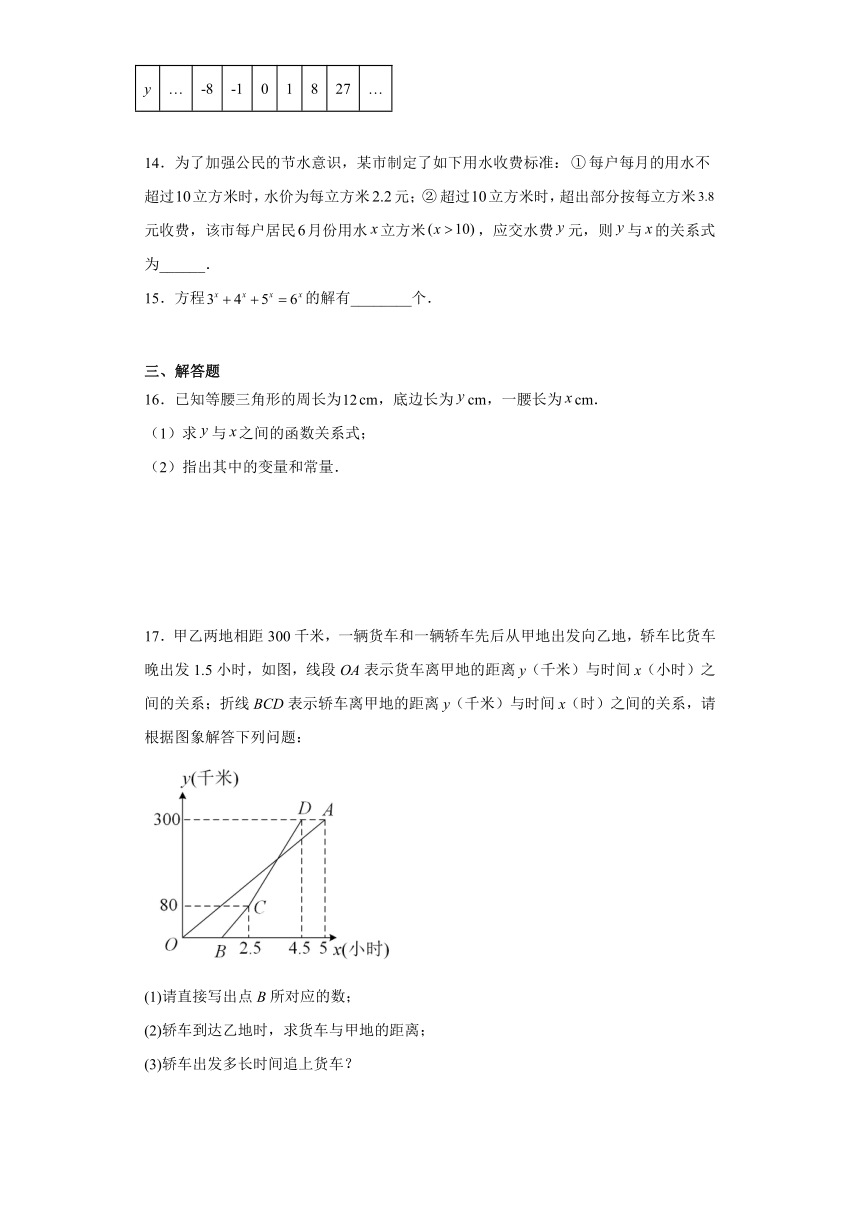
17.甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
18.在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
19.你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低(特别是二氧化碳)的排放量的一种生活方式.
(1)设家居用电的二氧化碳排放量为,耗电量为,则家居用电的二氧化碳排放量可以用关系式表示为______;
(2)在上述关系式中,耗电量每增加,二氧化碳排放量增加______;当耗电量从增加到时,二氧化碳排放从______增加到______;
(3)小明家本月家居用电大约,天然气,自来水,开私家车耗油,请你计算一下小明家这几项的二氧化碳排放量.
20.在平面直角坐标系中,O为坐标原点,选取x轴上一点A,建立平行四边形,与y轴交于点E,已知.
(1)如图1,求的长;
(2)如图2,为的角平分线,分别交y轴、于点F、D,,点P为平行四边形边上一动点,从A点出发,以2个单位长度/秒的速度,沿运动,到达C点停止运动.设的面积为S,运动时间为t,求S与t的函数关系式,并写出t的取值范围;
(3)如图3,在(2)的条件下,Q为的中点.当时,求的长.
参考答案
1.C
2.A
3.C
4.D
5.B
6.C
7.C
8.A
9.D
10.D
11.5
12.x≠2.
13.-64
14.
15.1
16.(1);(2),是变量;是常量.
17.(1)1.5
(2)轿车到达乙地时,货车与甲地的距离是270千米
(3)轿车出发2.4小时追上货车
18.①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
19.(1)y=0.785x
(2)0.785kg,0.785kg,78.5kg
(3)297.2kg
20.(1)解:如图,过点C作轴于点K,
∵,
∴,
∴;
(2)解:∵四边形是平行四边形,
∴,
∴,
∵为的角平分线,
∴,
∴,
∴,
∵,
∴,
当点P在线段上时,连接,过点O作于点T,
∵,
∴,
∴;
当点P在线段上时,
;
综上所述,;
(3)解:如图,连接,过点D作轴于点L,
∵,
∴,
∴,
∴,
∴,
即,
解得:,
∴,
∵,
∴,
即,
解得:,
∴,
∵Q为的中点,,
∴,
当点P在线段上时,,
∴,解得:,
∴,
∵,
∴点,
∴;
当点在线段上时,,
解得:,
∴,
∴,
∴,
∴;
综上所述,的长为或.
一、单选题
1.函数中自变量x的取值范围是( )
A. B. C. D.
2.如图,下列各曲线中,能够表示y是x的函数的是( )
A.(1)(2) B.(1)(4) C.(1)(2)(4) D.(1)(2)(3)(4)
3.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量
A.1个 B.2个 C.3个 D.4个
4.某水果销售商有100千克苹果,当苹果单价为15元/千克时,能全部销售完,市场调查表明苹果单价每提高1元,销售量减少6千克,若苹果单价提高x元,则苹果销售额y关于x的函数表达式为( )
A. B.
C. D.
5.下列各式中,表示y是x的函数的有( )
①2y+x=3;②y=x+2z;③y=2;④y=kx+1(k为常量);⑤y2=2x.
A.0个 B.1个 C.2个 D.3个
6.下列四个点中,在函数y=3x+1的图像上的是( )
A.(-1,2) B.(0,-1) C.(1,4) D.(2,-7)
7.在三角形面积公式S=ah,a=2cm中,下列说法正确的是( )
A.S,a是变量,h是常量 B.S,h是变量,是常量
C.S,h是变量,a是常量 D.S,h,a是变量,是常量
8.某学校用100元钱买乒乓球,所购买球的个数w与单价n(元)之间的关系是w=,其中( )
A.100是常量,w,n是变量
B.100,w是常量,n是变量
C.100,n是常量,w是变量
D.无法确定哪个是常量,哪个是变量
9.三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处点O与点P不重合利用仪器测量了的大小设蜜蜂飞行时间为的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.如果f(x)=3x-1,那么f(2)=_____________.
12.函数y=中,自变量x的取值范围是_____.
13.根据表格中的数据规律,当x=-4时,y的值是________.
x … -2 -1 0 1 2 3 …
y … -8 -1 0 1 8 27 …
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为______.
15.方程的解有________个.
三、解答题
16.已知等腰三角形的周长为cm,底边长为cm,一腰长为cm.
(1)求与之间的函数关系式;
(2)指出其中的变量和常量.
17.甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
18.在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
19.你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低(特别是二氧化碳)的排放量的一种生活方式.
(1)设家居用电的二氧化碳排放量为,耗电量为,则家居用电的二氧化碳排放量可以用关系式表示为______;
(2)在上述关系式中,耗电量每增加,二氧化碳排放量增加______;当耗电量从增加到时,二氧化碳排放从______增加到______;
(3)小明家本月家居用电大约,天然气,自来水,开私家车耗油,请你计算一下小明家这几项的二氧化碳排放量.
20.在平面直角坐标系中,O为坐标原点,选取x轴上一点A,建立平行四边形,与y轴交于点E,已知.
(1)如图1,求的长;
(2)如图2,为的角平分线,分别交y轴、于点F、D,,点P为平行四边形边上一动点,从A点出发,以2个单位长度/秒的速度,沿运动,到达C点停止运动.设的面积为S,运动时间为t,求S与t的函数关系式,并写出t的取值范围;
(3)如图3,在(2)的条件下,Q为的中点.当时,求的长.
参考答案
1.C
2.A
3.C
4.D
5.B
6.C
7.C
8.A
9.D
10.D
11.5
12.x≠2.
13.-64
14.
15.1
16.(1);(2),是变量;是常量.
17.(1)1.5
(2)轿车到达乙地时,货车与甲地的距离是270千米
(3)轿车出发2.4小时追上货车
18.①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
19.(1)y=0.785x
(2)0.785kg,0.785kg,78.5kg
(3)297.2kg
20.(1)解:如图,过点C作轴于点K,
∵,
∴,
∴;
(2)解:∵四边形是平行四边形,
∴,
∴,
∵为的角平分线,
∴,
∴,
∴,
∵,
∴,
当点P在线段上时,连接,过点O作于点T,
∵,
∴,
∴;
当点P在线段上时,
;
综上所述,;
(3)解:如图,连接,过点D作轴于点L,
∵,
∴,
∴,
∴,
∴,
即,
解得:,
∴,
∵,
∴,
即,
解得:,
∴,
∵Q为的中点,,
∴,
当点P在线段上时,,
∴,解得:,
∴,
∵,
∴点,
∴;
当点在线段上时,,
解得:,
∴,
∴,
∴,
∴;
综上所述,的长为或.
