直线与圆的位置关系[下学期]
文档属性
| 名称 | 直线与圆的位置关系[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-22 17:05:00 | ||
图片预览






文档简介
课件25张PPT。全品
中考复习方案
数学分册制作人:朱琨珂第八章第二课时:
直线和圆的位置关系要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦1.本课时重点是直线和圆的位置关系的性质和判定. 2.直线和圆的位置关系.设⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交? d<r
(2)直线l和⊙O相切? d=r
(3)直线l和⊙O相离? d>r 3、切线的判定和性质定理及推论.
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的性质定理及其推论.定理:圆的切线垂直于经过切点的半径.
推论1:经过圆心且垂直于切线的直线必经过切点.
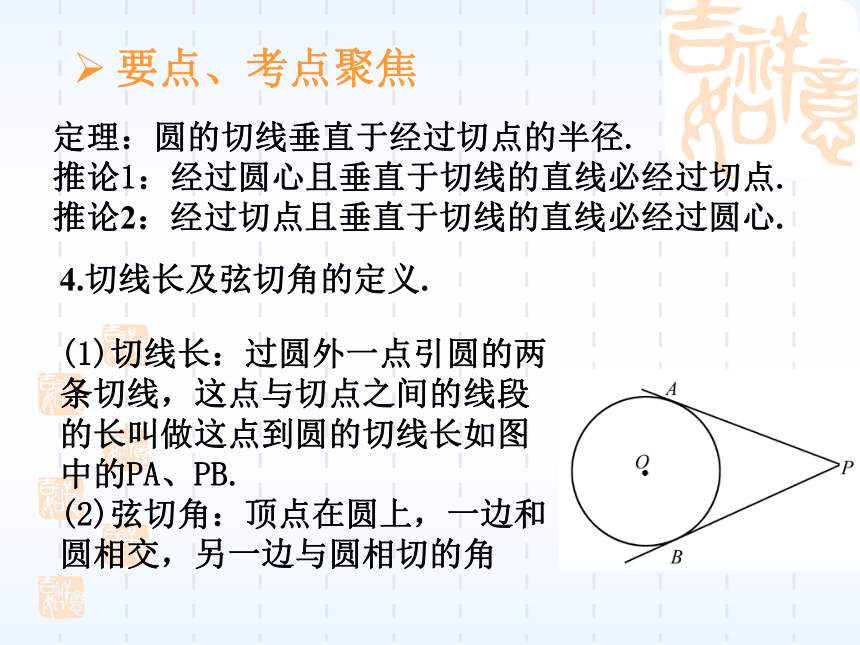
推论2:经过切点且垂直于切线的直线必经过圆心. 4.切线长及弦切角的定义. (1)切线长:过圆外一点引圆的两
条切线,这点与切点之间的线段
的长叫做这点到圆的切线长如图
中的PA、PB.
(2)弦切角:顶点在圆上,一边和
圆相交,另一边与圆相切的角要点、考点聚焦5.切线长定理及弦切角定理.(1)切线长定理:从圆外一点引圆的两条切线,它们的
切线长相等,圆心和这一点的连线平
分两条切线的夹角.(2)弦切角定理:弦切角等于它所夹的弧所对的圆周角. 6.三角形的内切圆和四边形的内切圆.(1)三角形的内切圆:和三角形各边都相切的圆. (2)三角形内心:内切圆的圆心.(3)三角形内切圆的性质:
①到三角形三边的距离相等,
②圆心和三角形各顶点的连线平分这个角.要点、考点聚焦(4)四边形的内切圆的性质:
圆外切四边形的对边和相等. 7.中考热点.直线和圆的位置关系是中考的热点,
特别是切线长定理、弦切角定理.
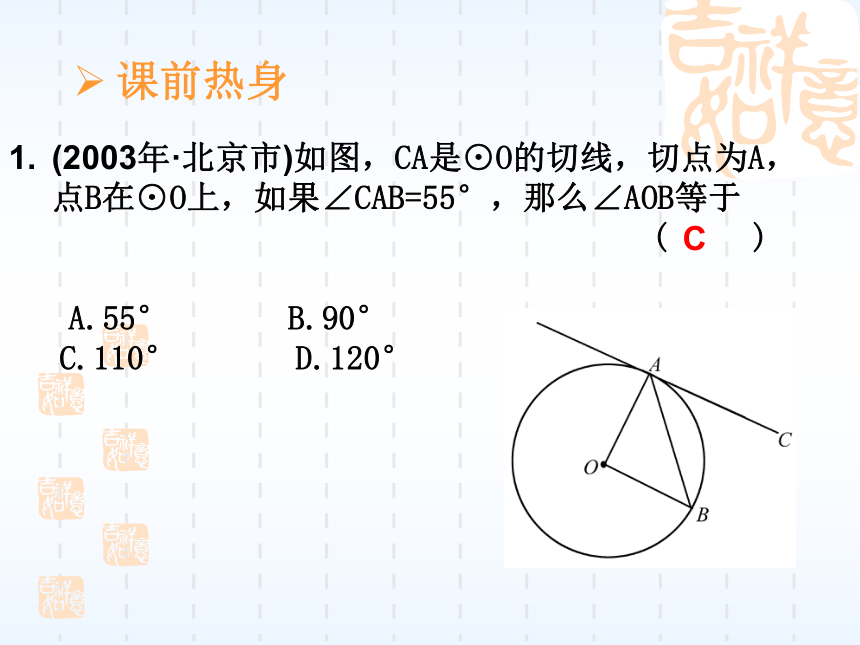
考题多以填空、选择、证明、综合题为主.要点、考点聚焦课前热身(2003年·北京市)如图,CA是⊙O的切线,切点为A,点B在⊙O上,如果∠CAB=55°,那么∠AOB等于
( )
A.55° B.90°
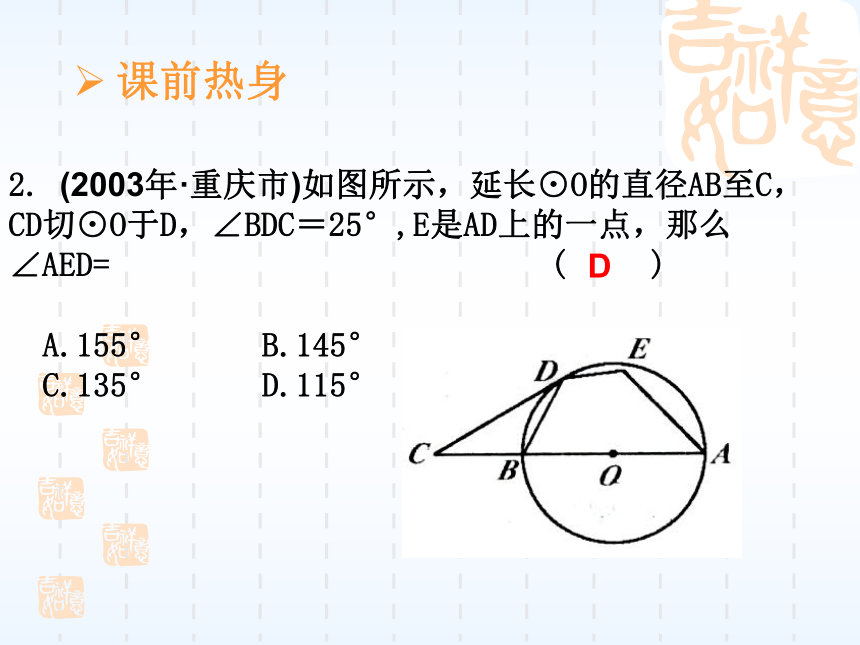
C.110° D.120° C2. (2003年·重庆市)如图所示,延长⊙O的直径AB至C,CD切⊙O于D,∠BDC=25°,E是AD上的一点,那么∠AED= ( )
A.155° B.145°
C.135° D.115° D课前热身3.下列命题中,正确的命题有( )
①圆的切线垂直于半径
②垂直于切线的直径必过圆心
③经过圆心且垂直于切线的直线过切点
④如果圆的两条切线平行,那么过两切点的直线
必过圆心
⑤三角形的内心不一定在三角形的内部
⑥多边形的内切圆圆心到各边的距离相等
A.2个 B.3个
C.4个 D.5个
B课前热身4.(2003年·武汉市)已知圆的半径为65 cm,如果一条直线和圆心的距离为9cm,那么这条直线和这个圆的位置关系是 ( )
A.相交 B.相切
C.相离 D.相交或相离 C5.等腰梯形外切于⊙O,⊙O的直径为6 cm,等腰梯形的腰长为8 cm,则梯形的面积为( )
A.24 cm2 B.48 cm2
C.36 cm 2 D.无法计算B课前热身典型例题解析【例1】(2004年·北京海淀)如图(1),A、K为⊙O上的两点,直线FN⊥MA,垂足为N,FN与⊙O相切于点F, ∠AOK=2∠MAK.(1)求证:MN是⊙O的切线;(2)若点B为⊙O上一动点,BO的延长线交⊙O于C,交NF于点D,连接AC并延长交NF于点E,当FD=2ED时,求∠AEN的余切值。 【解析】(1)∵∠O+2∠KAO=180°
∴2∠MAK+2∠KAO=180°
∴∠MAK+∠KAO=90°即OA⊥MN
∴MN是⊙O的切线【解析】
(2)此题分两种情况。如图(2)和图(3)。如图(2),连接AB、OF,可先证明
∠2=∠AEN CD=DE。
设⊙O的半径为r,ED=x,根据切
割线定量有DF2=DC·DB
(2x)2=x(x+2r)
cot∠AEN=如图(3),同样图(2)图(3)【例2】如图,在△ABC中,AC=BC,E是内心,
AE的延长线交△ABC的外接圆于D,
求证:
(1)BE=AE
(2)AB/AC=AE/DE典型例题解析【解析】
(1)要证BE=AE,则需证∠1=∠2,
由AC=BC?∠CAB=∠CBA,
想到AE、BE必是角平线,而E是内心,
所以AE、BE分别平分∠CAB、∠CBA.(2)要证比例式,应该先想到这几条线段在哪两个三角形中,再证相似,这是证明比例式(或等积式)的首选数学思路.但此题的四条线段不在两个三角形中,下面考虑的思路有两条:
一是等线段代换,
二是中间比.此题中若将AE换成BE,
则只要证△ABC∽△BED.ΔABC∽ΔBED【例3】在△ABC中,如图,BC=9,AC=12,AB=15,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E.
(1)求证:△ABC是直角三角形.
(2)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线.
(3)设⊙O交BC于点F,连结EF,求AE的长和EF∶AC的值. (2003年·广西)典型例题解析【解析】
(1)根据勾股定理的逆定理,
很容易证得. 【解析】
(2)要证切线,若这条直线上有一点在圆上,通常是过这一点作半径,证明半径垂直于这条直线即可,因此此题须连结OD,证OD⊥AC.
∵∠BDE=90°∴BE是⊙O的直径
∴OB=OD ∴ ∴OD⊥AC(3)通过平行或相似求解
OD∥BC
由∠BFE=90° EF∥AC【例4】直线l切⊙O于点C,AD为⊙O的任一条直径,点B在直线l上,且∠BAC=∠CAD(AB与AD不在一条直线上)画出图形,试判断四边形ABCO是怎样的特殊四边形?并证明你所得到的结论.【解析】本题可根据题意画出⊙O与它的切线l,再画直径AD,最后根据∠BAC=∠CAD,来确定B的位置.在探索四边形ABCO形状时,可转动直径AD,画出几个不同位置的图形进行观察,猜想,发现在一般情形下(即AD与l不行平时)四边形ABCO可能是直角梯形,而当AD∥l时,四边形ABCO变成了正方形,所以在解题时需分两种情况进行分类、讨论、证明,如下(1),(2)两图.典型例题解析AD不平行于l图(1)AD∥l图(2) 1.若证切线,有两条思路:
①是直线上的点不知是否在圆上的,则过圆心作该直线的垂线,根据定义证;
②是已知直线上的点在圆上,则连结圆心和这一点,根据切线的判定定理证明.
2.有切线,则常连结过切点的半径;若不知切
点,则过圆心作切线的垂线,则垂足为切点.
有切线,常利用弦切角计算或证明.方法小结:课时训练1.已知圆的直径为13 cm,圆心到直线l的距离为6cm,
那么直线l和这个圆的公共点个数是( )
A.0个 B.1个
C.2个 D.无法确定2.(2003年·山西省)如图,AB、AC是⊙O的两条切线,B、C是切点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115°
C.65°或115° D.130°或50°CC3.如图中,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连结AD,如果∠DAC=78°,那么∠ADO等于 ( )
A.70° B.64°
C.62° D.51°B课时训练4.如图,BC为半圆的直径,CA为切线,AB交半圆于E,EF⊥BC于F,连结EC,则图中与△EFC相似的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个D课时训练5.如图,PA,PB分别切⊙O于A、B,OP交⊙O于C,下列结论中错误的是 ( )
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.PA王2=PC·PBD课时训练6.如图,∠AOB=30°,OA=10,那么以A为圆心,6为半径的⊙A与射线OB的关系是 ( )
A.相交 B.相切
C.相离 D.不能确定A课时训练
中考复习方案
数学分册制作人:朱琨珂第八章第二课时:
直线和圆的位置关系要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦1.本课时重点是直线和圆的位置关系的性质和判定. 2.直线和圆的位置关系.设⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交? d<r
(2)直线l和⊙O相切? d=r
(3)直线l和⊙O相离? d>r 3、切线的判定和性质定理及推论.
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的性质定理及其推论.定理:圆的切线垂直于经过切点的半径.
推论1:经过圆心且垂直于切线的直线必经过切点.
推论2:经过切点且垂直于切线的直线必经过圆心. 4.切线长及弦切角的定义. (1)切线长:过圆外一点引圆的两
条切线,这点与切点之间的线段
的长叫做这点到圆的切线长如图
中的PA、PB.
(2)弦切角:顶点在圆上,一边和
圆相交,另一边与圆相切的角要点、考点聚焦5.切线长定理及弦切角定理.(1)切线长定理:从圆外一点引圆的两条切线,它们的
切线长相等,圆心和这一点的连线平
分两条切线的夹角.(2)弦切角定理:弦切角等于它所夹的弧所对的圆周角. 6.三角形的内切圆和四边形的内切圆.(1)三角形的内切圆:和三角形各边都相切的圆. (2)三角形内心:内切圆的圆心.(3)三角形内切圆的性质:
①到三角形三边的距离相等,
②圆心和三角形各顶点的连线平分这个角.要点、考点聚焦(4)四边形的内切圆的性质:
圆外切四边形的对边和相等. 7.中考热点.直线和圆的位置关系是中考的热点,
特别是切线长定理、弦切角定理.
考题多以填空、选择、证明、综合题为主.要点、考点聚焦课前热身(2003年·北京市)如图,CA是⊙O的切线,切点为A,点B在⊙O上,如果∠CAB=55°,那么∠AOB等于
( )
A.55° B.90°
C.110° D.120° C2. (2003年·重庆市)如图所示,延长⊙O的直径AB至C,CD切⊙O于D,∠BDC=25°,E是AD上的一点,那么∠AED= ( )
A.155° B.145°
C.135° D.115° D课前热身3.下列命题中,正确的命题有( )
①圆的切线垂直于半径
②垂直于切线的直径必过圆心
③经过圆心且垂直于切线的直线过切点
④如果圆的两条切线平行,那么过两切点的直线
必过圆心
⑤三角形的内心不一定在三角形的内部
⑥多边形的内切圆圆心到各边的距离相等
A.2个 B.3个
C.4个 D.5个
B课前热身4.(2003年·武汉市)已知圆的半径为65 cm,如果一条直线和圆心的距离为9cm,那么这条直线和这个圆的位置关系是 ( )
A.相交 B.相切
C.相离 D.相交或相离 C5.等腰梯形外切于⊙O,⊙O的直径为6 cm,等腰梯形的腰长为8 cm,则梯形的面积为( )
A.24 cm2 B.48 cm2
C.36 cm 2 D.无法计算B课前热身典型例题解析【例1】(2004年·北京海淀)如图(1),A、K为⊙O上的两点,直线FN⊥MA,垂足为N,FN与⊙O相切于点F, ∠AOK=2∠MAK.(1)求证:MN是⊙O的切线;(2)若点B为⊙O上一动点,BO的延长线交⊙O于C,交NF于点D,连接AC并延长交NF于点E,当FD=2ED时,求∠AEN的余切值。 【解析】(1)∵∠O+2∠KAO=180°
∴2∠MAK+2∠KAO=180°
∴∠MAK+∠KAO=90°即OA⊥MN
∴MN是⊙O的切线【解析】
(2)此题分两种情况。如图(2)和图(3)。如图(2),连接AB、OF,可先证明
∠2=∠AEN CD=DE。
设⊙O的半径为r,ED=x,根据切
割线定量有DF2=DC·DB
(2x)2=x(x+2r)
cot∠AEN=如图(3),同样图(2)图(3)【例2】如图,在△ABC中,AC=BC,E是内心,
AE的延长线交△ABC的外接圆于D,
求证:
(1)BE=AE
(2)AB/AC=AE/DE典型例题解析【解析】
(1)要证BE=AE,则需证∠1=∠2,
由AC=BC?∠CAB=∠CBA,
想到AE、BE必是角平线,而E是内心,
所以AE、BE分别平分∠CAB、∠CBA.(2)要证比例式,应该先想到这几条线段在哪两个三角形中,再证相似,这是证明比例式(或等积式)的首选数学思路.但此题的四条线段不在两个三角形中,下面考虑的思路有两条:
一是等线段代换,
二是中间比.此题中若将AE换成BE,
则只要证△ABC∽△BED.ΔABC∽ΔBED【例3】在△ABC中,如图,BC=9,AC=12,AB=15,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E.
(1)求证:△ABC是直角三角形.
(2)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线.
(3)设⊙O交BC于点F,连结EF,求AE的长和EF∶AC的值. (2003年·广西)典型例题解析【解析】
(1)根据勾股定理的逆定理,
很容易证得. 【解析】
(2)要证切线,若这条直线上有一点在圆上,通常是过这一点作半径,证明半径垂直于这条直线即可,因此此题须连结OD,证OD⊥AC.
∵∠BDE=90°∴BE是⊙O的直径
∴OB=OD ∴ ∴OD⊥AC(3)通过平行或相似求解
OD∥BC
由∠BFE=90° EF∥AC【例4】直线l切⊙O于点C,AD为⊙O的任一条直径,点B在直线l上,且∠BAC=∠CAD(AB与AD不在一条直线上)画出图形,试判断四边形ABCO是怎样的特殊四边形?并证明你所得到的结论.【解析】本题可根据题意画出⊙O与它的切线l,再画直径AD,最后根据∠BAC=∠CAD,来确定B的位置.在探索四边形ABCO形状时,可转动直径AD,画出几个不同位置的图形进行观察,猜想,发现在一般情形下(即AD与l不行平时)四边形ABCO可能是直角梯形,而当AD∥l时,四边形ABCO变成了正方形,所以在解题时需分两种情况进行分类、讨论、证明,如下(1),(2)两图.典型例题解析AD不平行于l图(1)AD∥l图(2) 1.若证切线,有两条思路:
①是直线上的点不知是否在圆上的,则过圆心作该直线的垂线,根据定义证;
②是已知直线上的点在圆上,则连结圆心和这一点,根据切线的判定定理证明.
2.有切线,则常连结过切点的半径;若不知切
点,则过圆心作切线的垂线,则垂足为切点.
有切线,常利用弦切角计算或证明.方法小结:课时训练1.已知圆的直径为13 cm,圆心到直线l的距离为6cm,
那么直线l和这个圆的公共点个数是( )
A.0个 B.1个
C.2个 D.无法确定2.(2003年·山西省)如图,AB、AC是⊙O的两条切线,B、C是切点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115°
C.65°或115° D.130°或50°CC3.如图中,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连结AD,如果∠DAC=78°,那么∠ADO等于 ( )
A.70° B.64°
C.62° D.51°B课时训练4.如图,BC为半圆的直径,CA为切线,AB交半圆于E,EF⊥BC于F,连结EC,则图中与△EFC相似的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个D课时训练5.如图,PA,PB分别切⊙O于A、B,OP交⊙O于C,下列结论中错误的是 ( )
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.PA王2=PC·PBD课时训练6.如图,∠AOB=30°,OA=10,那么以A为圆心,6为半径的⊙A与射线OB的关系是 ( )
A.相交 B.相切
C.相离 D.不能确定A课时训练
同课章节目录
