初一数学下册期末复习第7章相交线与平行线复习题(附答案)
文档属性
| 名称 | 初一数学下册期末复习第7章相交线与平行线复习题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 149.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-08 16:18:43 | ||
图片预览


文档简介
初一数学下册期末复习第7章相交线与平行线复习题
一.选择题(共10小题)
1.(2013 重庆) 如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )
A.40° B. 35° C. 50° D. 45°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3) (5)
2.(2013 永州)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
3.(2013 铜仁地区)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D. ∠BAC=∠ACD
4.(2013 娄底)下列图形中,由AB∥CD,能使∠1=∠2成立的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2013 抚顺)如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A. ∠1=∠3 B. ∠5=∠4 C. ∠5+∠3=180° D. ∠4+∠2=180°
6.(2013 北京)如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A. 40° B. 50° C. 70° D. 80°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6) (7) (8) (9)
7.(2012 梧州)如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠1=∠2 D. ∠D+∠ACD=180°
8.(2012 河池)如图,把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果∠1=25°,那么∠2的度数是( )
A. 30° B. 25° C. 20° D. 15°
9.(2011 仙桃)如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A. 23° B. 16° C. 20° D. 26°
10.(2011 怀化)如图,已知直线a∥b,∠1=40°,∠2=60°.则∠3等于( )
A. 100° B. 60° C. 40° D. 20°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10) (11) (12) (13)
二.填空题(共5小题)
11.(2013 镇江)如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=80°,则∠B= _________ °.
12.(2013 株洲)如图,直线l1∥ ( http: / / www.21cnjy.com )l2∥l3,点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC= _________ 度.
13.(2013 遂宁)如图,有一块含有6 ( http: / / www.21cnjy.com )0°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 _________ .
14.(2012 阜新)如图,一块直角三角板的两个顶点分别在直尺的对边上.若∠1=30°,那么∠2= _________ 度.
( http: / / www.21cnjy.com )
(14) (15)
15.(2011 六盘水)小明将两把直尺按 ( http: / / www.21cnjy.com )如图所示叠放,使其中一把直尺的一个顶点恰好落在另一把直尺的边上,则∠1+∠2= _________ 度.
三.解答题(共9小题)
16.(2009 淄博)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
( http: / / www.21cnjy.com )
17.(2005 广东)如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=40°,求∠2的度数.
( http: / / www.21cnjy.com )
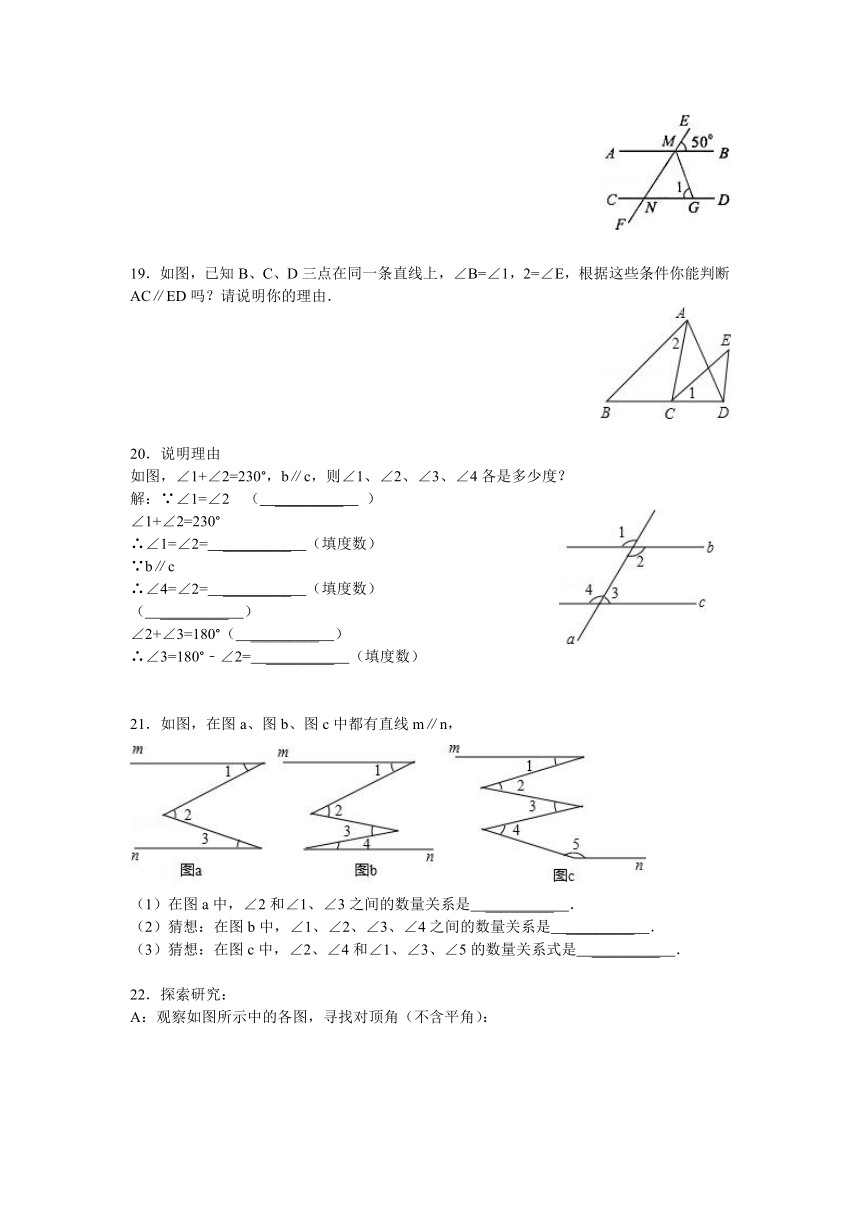
18.(2005 安徽)如 ( http: / / www.21cnjy.com )图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
19.如图,已知B、C、D三点在同一条直线上,∠B=∠1,2=∠E,根据这些条件你能判断AC∥ED吗?请说明你的理由.
( http: / / www.21cnjy.com )
20.说明理由
如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度?
解:∵∠1=∠2 ( _________ )
∠1+∠2=230°
∴∠1=∠2= _________ (填度数)
∵b∥c
∴∠4=∠2= _________ (填度数)
( _________ )
∠2+∠3=180°( _________ )
∴∠3=180°﹣∠2= _________ (填度数)
21.如图,在图a、图b、图c中都有直线m∥n,
( http: / / www.21cnjy.com )
(1)在图a中,∠2和∠1、∠3之间的数量关系是 _________ .
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是 _________ .
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是 _________ .
22.探索研究:
A:观察如图所示中的各图,寻找对顶角(不含平角):
( http: / / www.21cnjy.com )
(1)如图a,图中共有 _________ 对不同对顶角;
(2)如图b,图中共有 _________ 对不同的对顶角;
(3)如图c,图中共有 _________ 对不同的对顶角.
(4)研究(1)﹣(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 _________ 对对顶角
(5)计算2013条直线相交于一点,则可形成 _________ 对对顶角
B:
(1)3条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(2)4条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(3)n条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(4)计算2013条直线最多有 ___ ( http: / / www.21cnjy.com )______ 个交点,则可形成 _________ 对不同的对顶角,那么2013条直线最多形成 _________ 对不同的对顶角.
23.已知AB∥CD,分别探讨下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由.
( http: / / www.21cnjy.com )
24.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,如果∠AOD=40°.
求:(1)∠COP的度数;
(2)∠BOF的度数.
参考答案与试题解析
一.选择题(共10小题)
1.A.2.C.3.A.4.B.5.B.6.C.7.C.8.C.9.C.10.A.
二.填空题(共5小题)
11. 50 °.12.120 13. 12° 14.60 15. 90
16.解:∵AB∥CD,∠A=37°,∴∠ECD=∠A=37°.
∵DE⊥AE,∴∠D=90°﹣∠ECD=90°﹣37°=53°.
17. 解:∵AB∥CD,∴∠1=∠AEG.
∵EG平分∠AEF,∴∠1=∠GEF,∠AEF=2∠1.
又∵∠AEF+∠2=180°,∴∠2=180°﹣2∠1=180°﹣80°=100°.
18.解:∵∠EMB=50°,∴∠BMF=180°﹣∠EMB=130°.
∵MG平分∠BMF,∴∠BMG=∠BMF=65°,
∵AB∥CD,∴∠1=∠BMG=65°.
19.解:∵∠B=∠1,2=∠E,∴∠BCA=180°﹣∠B﹣∠2,∠BDE=180°﹣∠E﹣∠1,
∴∠BCA=∠BDE,∴AC∥ED.
20.
解:∵∠1=∠2(对顶角相等),∠1+∠2=230°,∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180°﹣∠2=65°,
故答案为:对顶角相等,115°,115°,两直线平行,内错角相等,两直线平行,同旁内角互补,65°.
21. ( http: / / www.21cnjy.com )
解:(1)如图,过∠2的顶点作m∥a,
∵m∥n,∴a∥m∥n,∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)∠2+∠4=∠1+∠3+180°﹣∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°﹣∠5.
22.A.解:(1)有2对对顶角;(2)有6对对顶角;(3)有12对对顶角;
(4)有n条直线时,有n(n﹣1)对对顶角;
(5)n=2013时,可形成2013×2012=4050156对顶角.
故答案为:2,6,12,n(n﹣1),4050156.
B解:(1)如图(1),可得三条直线两两相交,最多有3个交点;有6对对顶角.
(2)如图(2),可得四条直线两两相交,最多有6个交点;又12对对顶角.
(3)由(1)得,=3,由(2)得,=6;
∴可得,n条直线两两相交,最多有个交点(n为正整数,且n≥2).有n(n﹣1)对对顶角. ( http: / / www.21cnjy.com )
(4)当n=2013时,有2025078个交点,有4050156对对顶角.
故答案为3,6;6,12;,n(n﹣1);2025078,4050156,4050156,.
23.解:①过点P作PQ∥AB,
∵AB∥CD,∴PQ∥AB∥CD,∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
②过点P作PQ∥AB,
∵AB∥CD,∴PQ∥AB∥CD,∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,∴∠APC=∠PAB+∠PCD;
③∵AB∥CD,∴∠1=∠PCD,
∵∠1=∠PAB+∠APC,∴∠PCD=∠PAB+∠APC;
④∵AB∥CD,∴∠1=∠PAB,
∵∠1=∠PCD+∠APC,∴∠PAB=∠PCD+∠APC.
24.
解:(1)∵∠AOD=40°,
∴∠BOC=40°,
∵OP是∠BOC的平分线,
∴∠COP=20°;
(2)∵OF⊥CD,
∴∠DOF=90°,
∴∠AOF=130°,
∴∠BOF=180°﹣∠AOF=180°﹣130°=50°.
一.选择题(共10小题)
1.(2013 重庆) 如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )
A.40° B. 35° C. 50° D. 45°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3) (5)
2.(2013 永州)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B. ∠1=∠5 C. ∠1+∠3=180° D. ∠3=∠5
3.(2013 铜仁地区)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D. ∠BAC=∠ACD
4.(2013 娄底)下列图形中,由AB∥CD,能使∠1=∠2成立的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
5.(2013 抚顺)如图,直线l1、l2被直线l3、l4所截,下列条件中,不能判断直线l1∥l2的是( )
A. ∠1=∠3 B. ∠5=∠4 C. ∠5+∠3=180° D. ∠4+∠2=180°
6.(2013 北京)如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A. 40° B. 50° C. 70° D. 80°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6) (7) (8) (9)
7.(2012 梧州)如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠1=∠2 D. ∠D+∠ACD=180°
8.(2012 河池)如图,把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果∠1=25°,那么∠2的度数是( )
A. 30° B. 25° C. 20° D. 15°
9.(2011 仙桃)如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A. 23° B. 16° C. 20° D. 26°
10.(2011 怀化)如图,已知直线a∥b,∠1=40°,∠2=60°.则∠3等于( )
A. 100° B. 60° C. 40° D. 20°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(10) (11) (12) (13)
二.填空题(共5小题)
11.(2013 镇江)如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=80°,则∠B= _________ °.
12.(2013 株洲)如图,直线l1∥ ( http: / / www.21cnjy.com )l2∥l3,点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC= _________ 度.
13.(2013 遂宁)如图,有一块含有6 ( http: / / www.21cnjy.com )0°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 _________ .
14.(2012 阜新)如图,一块直角三角板的两个顶点分别在直尺的对边上.若∠1=30°,那么∠2= _________ 度.
( http: / / www.21cnjy.com )
(14) (15)
15.(2011 六盘水)小明将两把直尺按 ( http: / / www.21cnjy.com )如图所示叠放,使其中一把直尺的一个顶点恰好落在另一把直尺的边上,则∠1+∠2= _________ 度.
三.解答题(共9小题)
16.(2009 淄博)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
( http: / / www.21cnjy.com )
17.(2005 广东)如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=40°,求∠2的度数.
( http: / / www.21cnjy.com )
18.(2005 安徽)如 ( http: / / www.21cnjy.com )图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
19.如图,已知B、C、D三点在同一条直线上,∠B=∠1,2=∠E,根据这些条件你能判断AC∥ED吗?请说明你的理由.
( http: / / www.21cnjy.com )
20.说明理由
如图,∠1+∠2=230°,b∥c,则∠1、∠2、∠3、∠4各是多少度?
解:∵∠1=∠2 ( _________ )
∠1+∠2=230°
∴∠1=∠2= _________ (填度数)
∵b∥c
∴∠4=∠2= _________ (填度数)
( _________ )
∠2+∠3=180°( _________ )
∴∠3=180°﹣∠2= _________ (填度数)
21.如图,在图a、图b、图c中都有直线m∥n,
( http: / / www.21cnjy.com )
(1)在图a中,∠2和∠1、∠3之间的数量关系是 _________ .
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是 _________ .
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是 _________ .
22.探索研究:
A:观察如图所示中的各图,寻找对顶角(不含平角):
( http: / / www.21cnjy.com )
(1)如图a,图中共有 _________ 对不同对顶角;
(2)如图b,图中共有 _________ 对不同的对顶角;
(3)如图c,图中共有 _________ 对不同的对顶角.
(4)研究(1)﹣(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 _________ 对对顶角
(5)计算2013条直线相交于一点,则可形成 _________ 对对顶角
B:
(1)3条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(2)4条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(3)n条直线两两相交最多有 _________ 个交点,此时有 _________ 对不同的对顶角
(4)计算2013条直线最多有 ___ ( http: / / www.21cnjy.com )______ 个交点,则可形成 _________ 对不同的对顶角,那么2013条直线最多形成 _________ 对不同的对顶角.
23.已知AB∥CD,分别探讨下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由.
( http: / / www.21cnjy.com )
24.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OF⊥CD,如果∠AOD=40°.
求:(1)∠COP的度数;
(2)∠BOF的度数.
参考答案与试题解析
一.选择题(共10小题)
1.A.2.C.3.A.4.B.5.B.6.C.7.C.8.C.9.C.10.A.
二.填空题(共5小题)
11. 50 °.12.120 13. 12° 14.60 15. 90
16.解:∵AB∥CD,∠A=37°,∴∠ECD=∠A=37°.
∵DE⊥AE,∴∠D=90°﹣∠ECD=90°﹣37°=53°.
17. 解:∵AB∥CD,∴∠1=∠AEG.
∵EG平分∠AEF,∴∠1=∠GEF,∠AEF=2∠1.
又∵∠AEF+∠2=180°,∴∠2=180°﹣2∠1=180°﹣80°=100°.
18.解:∵∠EMB=50°,∴∠BMF=180°﹣∠EMB=130°.
∵MG平分∠BMF,∴∠BMG=∠BMF=65°,
∵AB∥CD,∴∠1=∠BMG=65°.
19.解:∵∠B=∠1,2=∠E,∴∠BCA=180°﹣∠B﹣∠2,∠BDE=180°﹣∠E﹣∠1,
∴∠BCA=∠BDE,∴AC∥ED.
20.
解:∵∠1=∠2(对顶角相等),∠1+∠2=230°,∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180°﹣∠2=65°,
故答案为:对顶角相等,115°,115°,两直线平行,内错角相等,两直线平行,同旁内角互补,65°.
21. ( http: / / www.21cnjy.com )
解:(1)如图,过∠2的顶点作m∥a,
∵m∥n,∴a∥m∥n,∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)∠2+∠4=∠1+∠3+180°﹣∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°﹣∠5.
22.A.解:(1)有2对对顶角;(2)有6对对顶角;(3)有12对对顶角;
(4)有n条直线时,有n(n﹣1)对对顶角;
(5)n=2013时,可形成2013×2012=4050156对顶角.
故答案为:2,6,12,n(n﹣1),4050156.
B解:(1)如图(1),可得三条直线两两相交,最多有3个交点;有6对对顶角.
(2)如图(2),可得四条直线两两相交,最多有6个交点;又12对对顶角.
(3)由(1)得,=3,由(2)得,=6;
∴可得,n条直线两两相交,最多有个交点(n为正整数,且n≥2).有n(n﹣1)对对顶角. ( http: / / www.21cnjy.com )
(4)当n=2013时,有2025078个交点,有4050156对对顶角.
故答案为3,6;6,12;,n(n﹣1);2025078,4050156,4050156,.
23.解:①过点P作PQ∥AB,
∵AB∥CD,∴PQ∥AB∥CD,∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
②过点P作PQ∥AB,
∵AB∥CD,∴PQ∥AB∥CD,∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,∴∠APC=∠PAB+∠PCD;
③∵AB∥CD,∴∠1=∠PCD,
∵∠1=∠PAB+∠APC,∴∠PCD=∠PAB+∠APC;
④∵AB∥CD,∴∠1=∠PAB,
∵∠1=∠PCD+∠APC,∴∠PAB=∠PCD+∠APC.
24.
解:(1)∵∠AOD=40°,
∴∠BOC=40°,
∵OP是∠BOC的平分线,
∴∠COP=20°;
(2)∵OF⊥CD,
∴∠DOF=90°,
∴∠AOF=130°,
∴∠BOF=180°﹣∠AOF=180°﹣130°=50°.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
