人教版 八年级下册《18.2.1矩形》说课课件(共33张PPT)
文档属性
| 名称 | 人教版 八年级下册《18.2.1矩形》说课课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 07:29:06 | ||
图片预览










文档简介
(共33张PPT)
人教版义务教育课程标准实验教科书数学八年级下册
一、说教材
二、说教法
三、说学法
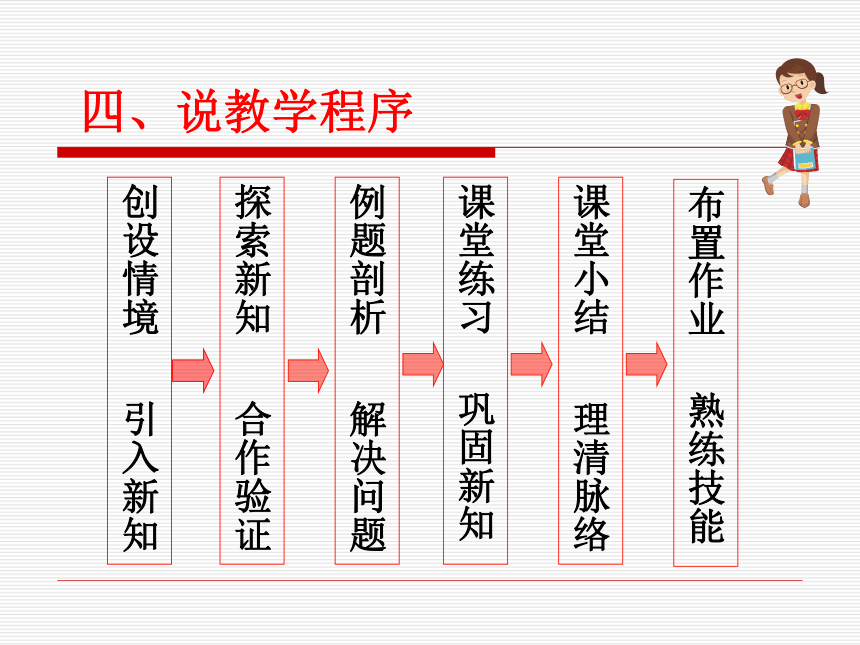
四、说教学程序
◇
◇
◇
◇
◇
◇
五、说板书设计
六、说教学评价与反思
一、说教材
(一)地位与作用
本节课是在学生已经学习了三角形、平行四边形积累一定的经验的基础上学习的,它是本章的重点内容之一,既是平行四边形知识的延伸,又为学习其它特殊平行四边形提供了研究方法和学习策略,同时培养学生分析问题和解决问题的能力,也为今后学习其他有关知识奠定了基础,起着承上启下的重要作用。
(二)学情分析
学生通过前一段时间对平行四边形相关知识的探究,已经具有一定的独立思考和探究问题的能力,但学生学习几何的时间不长,学习程度较浅,在探索中缺乏自主性。
一、说教材
(三)教学目标
1、知识与技能
(1)掌握矩形的概念和性质,理解矩形与平行四边形的区别
与联系。
(2)会初步运用矩形的概念和性质来解决有关问题
2、过程与方法
经历探索矩形的概念和性质的过程,发展学生合情推理的
意识,掌握几何思维方法,并渗透运动联系,从量变到质变的
观点。
3、情感态度与价值观
培养严谨的推理能力,以及自主合作的精神,体会逻辑推
理的思维价值,体会矩形的对称美和应用美。
一、说教材
(四)教学重、难点
重点:矩形的性质及其推论
难点:掌握矩形性质及其推论并用他
们解决矩形的相关问题。
一、说教材
在教师的引导下,创设情境,通过实验操作、猜想、直观演示、类比和引导发现相结合的教学方法,来启发学生思考,在思考中体会数学概念形成的过程中所蕴含的数学方法,使之获得内心感受。并借助多媒体辅助教学。
二、说教法
在本节课中不断指导学生学会学习,鼓励学生动手实践,主动探索与合作交流,变“被动学习”为“主动学习”,使每位学生都参与到学习过程中,同时获得轻松、愉快、成功的情感体验。
三、说学法
四、说教学程序
例题剖析 解决问题
探索新知 合作验证
创设情境 引入新知
课堂练习 巩固新知
课堂小结 理清脉络
布置作业 熟练技能
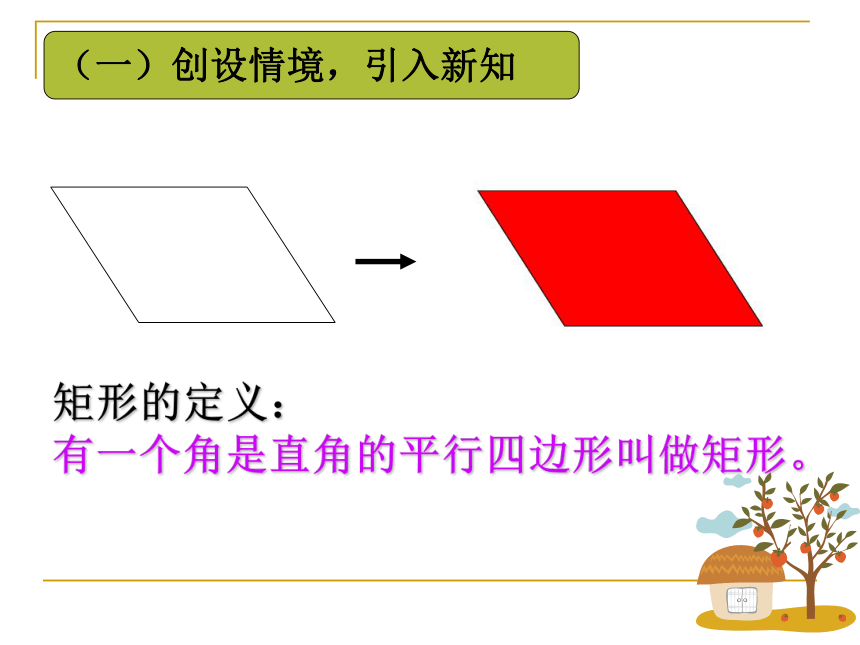
(一)创设情境,引入新知
矩形的定义:
有一个角是直角的平行四边形叫做矩形。
(一)创设情境,引入新知
矩形具有平行四边形所有的性质吗?
活动一:请个别学生口述平行四边形具备的所有
性质。
(二)探索新知,合作验证
结论1:矩形的四个角都是直角
结论2:矩形的对角线相等
活动二:探究矩形的性质
(二)探索新知,合作验证
引导性问题:
1、对比矩形和平行四边形的定义,矩形比平行
四边形多了一个什么条件?
2、增加了这个条件之后,矩形是否具备了它特
有的性质?
活动三:对所得到的两个结论进行理论上的
证明。
增强学生符号感、培养学生
演绎推理能力
(二)探索新知,合作验证
已知:四边形ABCD是矩形,∠C=90°,
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
(二)探索新知,合作验证
证明:∵四边形ABCD是矩形,∠C=90°
∴ ∠A= ∠C=90°, ∠D= ∠B
又∵ ∠A+ ∠B+∠C+∠D=360°
∠B+ ∠D=180°
∴ ∠D= ∠B=90°
即∠A=∠B=∠C=∠D=90°
(二)探索新知,合作验证
(方法一)
性质 1:矩形的四个角都是直角
D
C
B
A
证明:∵四边形ABCD是矩形,∠C=90°
∴AB∥CD,AD∥BC
∴∠B+∠C=180°, ∠D+∠C=180°,
∠B+∠A=180°
∴∠B=180°- ∠C=180°- 90°=90°
∠D=180°- ∠C=180°-90°=90°
∠A=180°- ∠B=180°-90°=90°
即∠A= ∠B=∠C= ∠D=90°
(二)探索新知,合作验证
性质 1:矩形的四个角都是直角
(方法二)
D
C
B
A
已知:四边形ABCD是矩形 ,
求证:AC = BD
A
B
C
D
(二)探索新知,合作验证
A
B
C
D
(二)探索新知,合作验证
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
性质 2:矩形的对角线相等
(方法一)
(方法二)
证明: ∵四边形ABCD是矩形
∴AB=DC,∠ABC=∠DCB=90°
∴在RT⊿ABC和RT⊿DCB中
AC2=AB2+BC2
BD2=DC2+BC2
∴AC=BD
(二)探索新知,合作验证
性质 2:矩形的对角线相等
A
B
C
D
(二)探索新知,合作验证
活动四:
在矩形ABCD中,
(1)图中存在直角三角形吗?共有几个直角三角形?
(2)在直角三角形ABC中,OB与AC之间有什么数量关系?为什么?由此可以得出什么结论?
结论:直角三角形斜边上的中线等于斜边的一半。
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
∵AD = BD ,CD = ED
∴四边形ACBE是平行四边形,
又∵∠ACB = 90°
∴平行性四边形ACBE是矩形
∴CE = AB
∵CD= CE ∴CD= AB
A
B
C
D
E
(二)探索新知,合作验证
推论:直角三角形斜边上的中线等于斜边的一半。
几何语言:在直角三
角形中,OB是中线,
则BO= AC
例1 如图,矩形ABCD的两条对角线相交于点
O,AB=4cm,
∠AOB=60°,
求矩形对角线的长。
(三)例题剖析,解决问题
活动一:
例1 如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。
解:∵四边形ABCD是矩形
∴AC与BD相等且互相平分
∴OA=OB
又∠AOB=60°,
∴ ⊿OAB是等边三角形
∴OA=AB=4cm
∴矩形的对角线长AC=BD=2OA=8cm
答:矩形的对角线长为8cm。
(三)例题剖析,解决问题
例1 如图,矩形ABCD的两条对角线相交于点
O,AB=4cm,
点O到AB的距离为3cm,
∠AOB=60°,
求矩形对角线的长。
求矩形的周长、面积和对角线的长。
培养学生对知识的综合
应用能力
(三)例题剖析,解决问题
E
活动二:
解:∵四边形ABCD是矩形
∴AC与BD相等且互相平分
∴OA=OB
又∵OE⊥AB
∴E是AB的中点
∴BC=2EO=6cm
∴C矩形ABCD=2×(AB+BC)=2×(4+6)=20cm
S矩形ABCD=AB×BC=4×6=24cm2
AC= cm
答:矩形的周长为20cm,面积为24 cm2 ,对角线为 cm。
E
(三)例题剖析,解决问题
1、矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
2、如图,四边形ABCD是矩形,
(1)AB= ,BC= ,AO= =BO= ,AC= ;
(2)∠AOB= , ∠AOD= , ∠BAC= ,
∠DAC= , ∠ABD= .
(四)课堂练习,巩固新知
3、在矩形ABCD中,AE⊥BD于E,若BE=OE=1,
则AC= , AB= 。
4、如果矩形的一条对角线长为8cm,两条对角
线的一个交角为120°,求矩形的边长。
(四)课堂练习,巩固新知
◇1.矩形的定义
◇2.矩形的性质:
矩形的四个角都等于直角
矩形的对角线相等
◇3.矩形的性质的推论:
直角三角形斜边上的中线等于斜边的一半
(五)课堂小结,理清脉络
一、必做题
课本P102 4
如图:已知在矩形ABCD中,对角线AC与BD相交
于o,∠ACB=30°,AB=5㎝,则
AC= ㎝,BD= ㎝
二、选做题
已知:如图BE、CF是△ABC
的两条高,M为BC的中点,分
别连ME、MF。
求证: (1)ME= BC (2)ME=MF
A
B
C
M
F
E
(六)布置作业,熟练技能
1、矩形的定义
2、矩形的性质
①
②
3、矩形性质的推论 §19.2.1 矩形
例题:
练习
六、评价与反思
本节课设计的每一个环节都是以学生为主,充分
体现新课程的理念。对于新知识的获取能够建立在
学生已有的知识基础之上,让学生自己动手探索完
成并体会到自己进行的探索是有意义的,有价值的
能培养其他们在学习上的自信心,也便于激发他们
对学习的浓厚兴趣,另外,学生对自己探索出来的
结论,记忆也会更加深刻久远,理解也更加深刻到
位,这样一种教学方法,更加有助于学生完善学习
过程,学生的探索创新思维、创新精神和创造能力
都将获得极大的提高。
人教版义务教育课程标准实验教科书数学八年级下册
一、说教材
二、说教法
三、说学法
四、说教学程序
◇
◇
◇
◇
◇
◇
五、说板书设计
六、说教学评价与反思
一、说教材
(一)地位与作用
本节课是在学生已经学习了三角形、平行四边形积累一定的经验的基础上学习的,它是本章的重点内容之一,既是平行四边形知识的延伸,又为学习其它特殊平行四边形提供了研究方法和学习策略,同时培养学生分析问题和解决问题的能力,也为今后学习其他有关知识奠定了基础,起着承上启下的重要作用。
(二)学情分析
学生通过前一段时间对平行四边形相关知识的探究,已经具有一定的独立思考和探究问题的能力,但学生学习几何的时间不长,学习程度较浅,在探索中缺乏自主性。
一、说教材
(三)教学目标
1、知识与技能
(1)掌握矩形的概念和性质,理解矩形与平行四边形的区别
与联系。
(2)会初步运用矩形的概念和性质来解决有关问题
2、过程与方法
经历探索矩形的概念和性质的过程,发展学生合情推理的
意识,掌握几何思维方法,并渗透运动联系,从量变到质变的
观点。
3、情感态度与价值观
培养严谨的推理能力,以及自主合作的精神,体会逻辑推
理的思维价值,体会矩形的对称美和应用美。
一、说教材
(四)教学重、难点
重点:矩形的性质及其推论
难点:掌握矩形性质及其推论并用他
们解决矩形的相关问题。
一、说教材
在教师的引导下,创设情境,通过实验操作、猜想、直观演示、类比和引导发现相结合的教学方法,来启发学生思考,在思考中体会数学概念形成的过程中所蕴含的数学方法,使之获得内心感受。并借助多媒体辅助教学。
二、说教法
在本节课中不断指导学生学会学习,鼓励学生动手实践,主动探索与合作交流,变“被动学习”为“主动学习”,使每位学生都参与到学习过程中,同时获得轻松、愉快、成功的情感体验。
三、说学法
四、说教学程序
例题剖析 解决问题
探索新知 合作验证
创设情境 引入新知
课堂练习 巩固新知
课堂小结 理清脉络
布置作业 熟练技能
(一)创设情境,引入新知
矩形的定义:
有一个角是直角的平行四边形叫做矩形。
(一)创设情境,引入新知
矩形具有平行四边形所有的性质吗?
活动一:请个别学生口述平行四边形具备的所有
性质。
(二)探索新知,合作验证
结论1:矩形的四个角都是直角
结论2:矩形的对角线相等
活动二:探究矩形的性质
(二)探索新知,合作验证
引导性问题:
1、对比矩形和平行四边形的定义,矩形比平行
四边形多了一个什么条件?
2、增加了这个条件之后,矩形是否具备了它特
有的性质?
活动三:对所得到的两个结论进行理论上的
证明。
增强学生符号感、培养学生
演绎推理能力
(二)探索新知,合作验证
已知:四边形ABCD是矩形,∠C=90°,
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
(二)探索新知,合作验证
证明:∵四边形ABCD是矩形,∠C=90°
∴ ∠A= ∠C=90°, ∠D= ∠B
又∵ ∠A+ ∠B+∠C+∠D=360°
∠B+ ∠D=180°
∴ ∠D= ∠B=90°
即∠A=∠B=∠C=∠D=90°
(二)探索新知,合作验证
(方法一)
性质 1:矩形的四个角都是直角
D
C
B
A
证明:∵四边形ABCD是矩形,∠C=90°
∴AB∥CD,AD∥BC
∴∠B+∠C=180°, ∠D+∠C=180°,
∠B+∠A=180°
∴∠B=180°- ∠C=180°- 90°=90°
∠D=180°- ∠C=180°-90°=90°
∠A=180°- ∠B=180°-90°=90°
即∠A= ∠B=∠C= ∠D=90°
(二)探索新知,合作验证
性质 1:矩形的四个角都是直角
(方法二)
D
C
B
A
已知:四边形ABCD是矩形 ,
求证:AC = BD
A
B
C
D
(二)探索新知,合作验证
A
B
C
D
(二)探索新知,合作验证
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
性质 2:矩形的对角线相等
(方法一)
(方法二)
证明: ∵四边形ABCD是矩形
∴AB=DC,∠ABC=∠DCB=90°
∴在RT⊿ABC和RT⊿DCB中
AC2=AB2+BC2
BD2=DC2+BC2
∴AC=BD
(二)探索新知,合作验证
性质 2:矩形的对角线相等
A
B
C
D
(二)探索新知,合作验证
活动四:
在矩形ABCD中,
(1)图中存在直角三角形吗?共有几个直角三角形?
(2)在直角三角形ABC中,OB与AC之间有什么数量关系?为什么?由此可以得出什么结论?
结论:直角三角形斜边上的中线等于斜边的一半。
已知△ABC中∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
∵AD = BD ,CD = ED
∴四边形ACBE是平行四边形,
又∵∠ACB = 90°
∴平行性四边形ACBE是矩形
∴CE = AB
∵CD= CE ∴CD= AB
A
B
C
D
E
(二)探索新知,合作验证
推论:直角三角形斜边上的中线等于斜边的一半。
几何语言:在直角三
角形中,OB是中线,
则BO= AC
例1 如图,矩形ABCD的两条对角线相交于点
O,AB=4cm,
∠AOB=60°,
求矩形对角线的长。
(三)例题剖析,解决问题
活动一:
例1 如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。
解:∵四边形ABCD是矩形
∴AC与BD相等且互相平分
∴OA=OB
又∠AOB=60°,
∴ ⊿OAB是等边三角形
∴OA=AB=4cm
∴矩形的对角线长AC=BD=2OA=8cm
答:矩形的对角线长为8cm。
(三)例题剖析,解决问题
例1 如图,矩形ABCD的两条对角线相交于点
O,AB=4cm,
点O到AB的距离为3cm,
∠AOB=60°,
求矩形对角线的长。
求矩形的周长、面积和对角线的长。
培养学生对知识的综合
应用能力
(三)例题剖析,解决问题
E
活动二:
解:∵四边形ABCD是矩形
∴AC与BD相等且互相平分
∴OA=OB
又∵OE⊥AB
∴E是AB的中点
∴BC=2EO=6cm
∴C矩形ABCD=2×(AB+BC)=2×(4+6)=20cm
S矩形ABCD=AB×BC=4×6=24cm2
AC= cm
答:矩形的周长为20cm,面积为24 cm2 ,对角线为 cm。
E
(三)例题剖析,解决问题
1、矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
2、如图,四边形ABCD是矩形,
(1)AB= ,BC= ,AO= =BO= ,AC= ;
(2)∠AOB= , ∠AOD= , ∠BAC= ,
∠DAC= , ∠ABD= .
(四)课堂练习,巩固新知
3、在矩形ABCD中,AE⊥BD于E,若BE=OE=1,
则AC= , AB= 。
4、如果矩形的一条对角线长为8cm,两条对角
线的一个交角为120°,求矩形的边长。
(四)课堂练习,巩固新知
◇1.矩形的定义
◇2.矩形的性质:
矩形的四个角都等于直角
矩形的对角线相等
◇3.矩形的性质的推论:
直角三角形斜边上的中线等于斜边的一半
(五)课堂小结,理清脉络
一、必做题
课本P102 4
如图:已知在矩形ABCD中,对角线AC与BD相交
于o,∠ACB=30°,AB=5㎝,则
AC= ㎝,BD= ㎝
二、选做题
已知:如图BE、CF是△ABC
的两条高,M为BC的中点,分
别连ME、MF。
求证: (1)ME= BC (2)ME=MF
A
B
C
M
F
E
(六)布置作业,熟练技能
1、矩形的定义
2、矩形的性质
①
②
3、矩形性质的推论 §19.2.1 矩形
例题:
练习
六、评价与反思
本节课设计的每一个环节都是以学生为主,充分
体现新课程的理念。对于新知识的获取能够建立在
学生已有的知识基础之上,让学生自己动手探索完
成并体会到自己进行的探索是有意义的,有价值的
能培养其他们在学习上的自信心,也便于激发他们
对学习的浓厚兴趣,另外,学生对自己探索出来的
结论,记忆也会更加深刻久远,理解也更加深刻到
位,这样一种教学方法,更加有助于学生完善学习
过程,学生的探索创新思维、创新精神和创造能力
都将获得极大的提高。
