第二十九讲 直线与圆的位置关系[下学期]
文档属性
| 名称 | 第二十九讲 直线与圆的位置关系[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 46.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-26 19:09:00 | ||
图片预览


文档简介
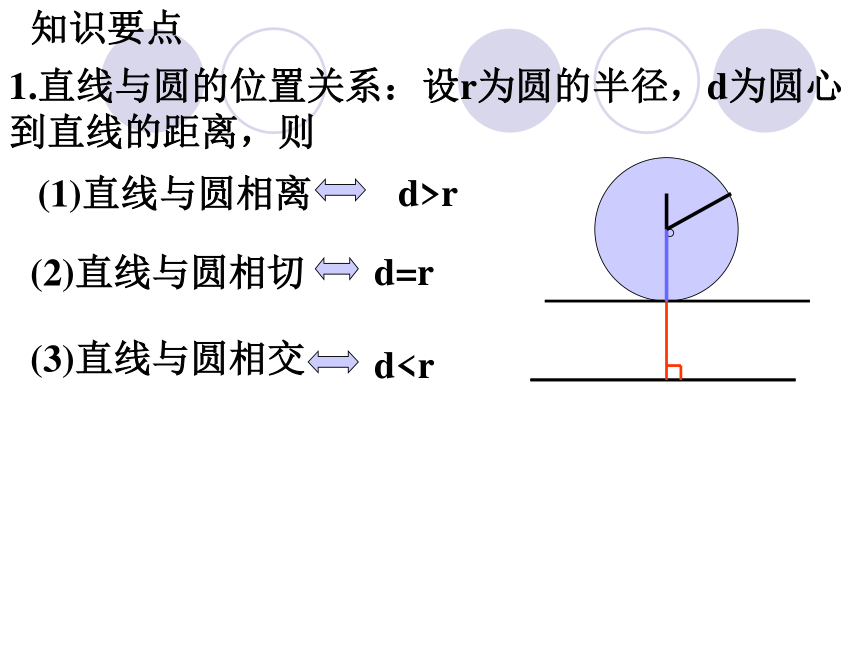
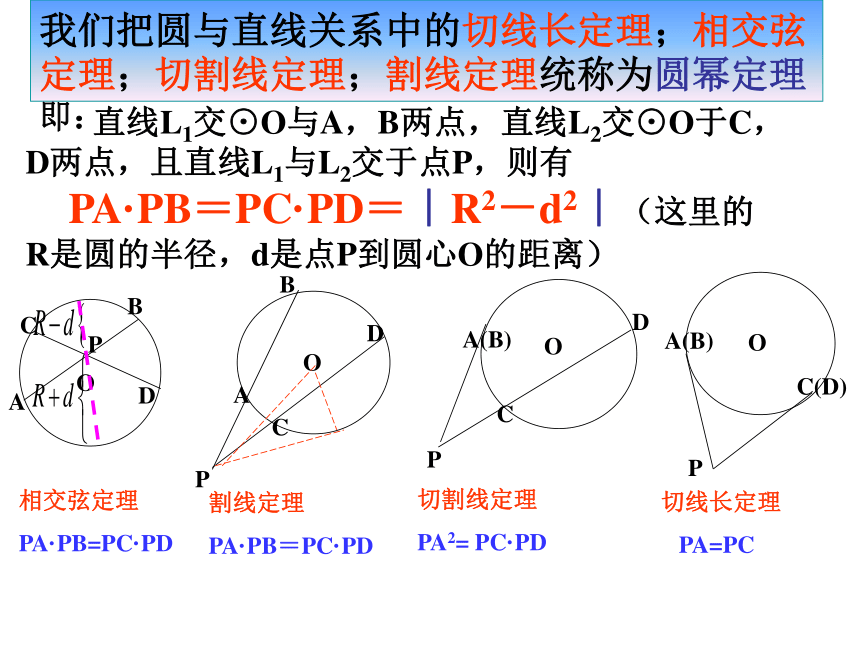
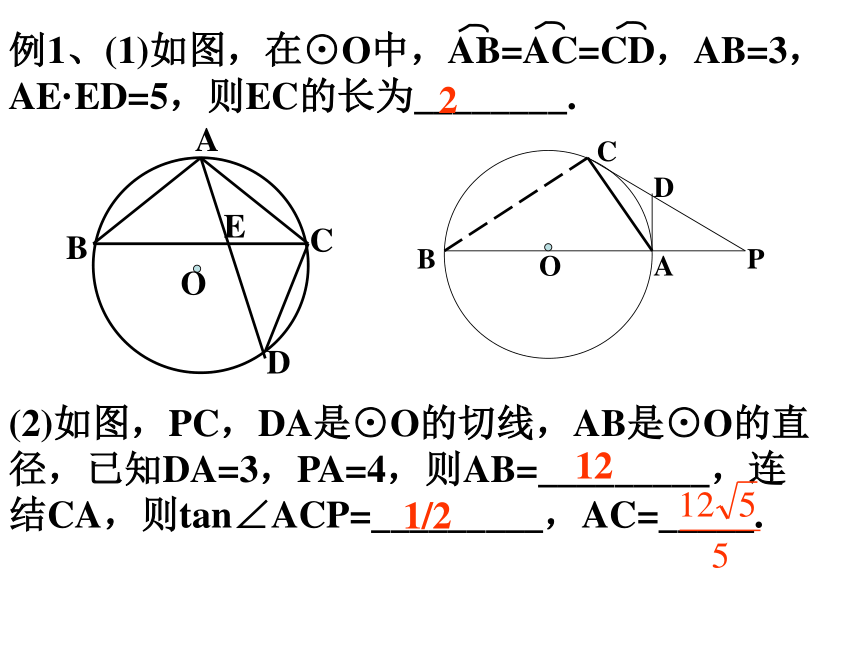
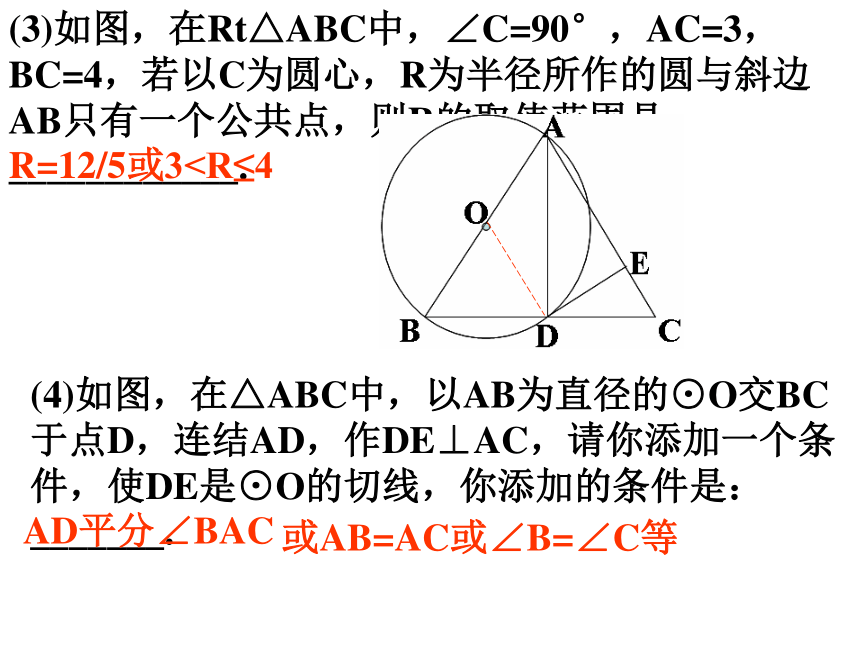
课件12张PPT。直线与圆的位置关系知识要点1.直线与圆的位置关系:设r为圆的半径,d为圆心到直线的距离,则 d>rd=rd PA·PB=PC·PD=|R2-d2|(这里的R是圆的半径,d是点P到圆心O的距离)(2)如图,PC,DA是⊙O的切线,AB是⊙O的直径,已知DA=3,PA=4,则AB=_________,连结CA,则tan∠ACP=_________,AC=_____.121/22(3)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是____________.R=12/5或3(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.例3、已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点为C.
(1)当点P在延长线上的位置如图时,连结AC,作∠APC的平分线,交AC于D,请量出∠CDP的度数.
(2)猜想∠CDP的度数是否随P在AB延长线上移动而变化,并证明之.例4、已知:如图,AC是⊙O的直径,BC切⊙O于C,AB交⊙O于点D,连结DO并延长交⊙O于点G,交BC延长线于点E,F是BC中点,连结DF,如果DF=5,且AD:DB=1:4. (1)求证:DF是⊙O的切线; (2)求GE的长.例5、如图,在平行四边形ABCD中,E是边BC上一点,AE⊥BC,以AE为直径作圆,圆心为O,连结CO、DO,如果该圆的半径AO恰好是CE与AD的比例中项.(1)求证:CO⊥DO; (2)判断CD与⊙O的位置关系,并证明你的判断. (3)如果tanB=4/3,AD=x,BE=y,求y与x的函数解析式,并写出自变量x的取值范围.例6.已知等边△ABC边长为a,D、E分别为AB、AC边上的动点,且在运动时保持DE∥BC,如图(1),⊙O1与⊙O2都不在△ABC的外部,且⊙O1、⊙O2分别与∠B和∠C的两边及DE都相切,其中和DE、BC的切点分别为M、N、M′、N′.
(1)求证:⊙O1和⊙O2是等圆;(2)设⊙O1的半径长为x,圆心距O1O2为y,求y与x的函数关系式,并写出x的取值范围;(3)当⊙O1与⊙O2外切时,求x的值.
(4)如图(2),当D、E分别是AB、AC边的中点时,将⊙O2先向左平移至和⊙O1重合,然后将重合后的圆沿着△ABC内各边按图(2)中箭头的方向进行滚动,且总是与△ABC的边相切,当点O1第一次回到它原来的位置时,求点O1经过的路线长度.
(2)连接EO交AD于点F,求证:EF=2FO.例3、已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点为C.
(1)当点P在延长线上的位置如图时,连结AC,作∠APC的平分线,交AC于D,请量出∠CDP的度数.
(2)猜想∠CDP的度数是否随P在AB延长线上移动而变化,并证明之.例4、已知:如图,AC是⊙O的直径,BC切⊙O于C,AB交⊙O于点D,连结DO并延长交⊙O于点G,交BC延长线于点E,F是BC中点,连结DF,如果DF=5,且AD:DB=1:4. (1)求证:DF是⊙O的切线; (2)求GE的长.例5、如图,在平行四边形ABCD中,E是边BC上一点,AE⊥BC,以AE为直径作圆,圆心为O,连结CO、DO,如果该圆的半径AO恰好是CE与AD的比例中项.(1)求证:CO⊥DO; (2)判断CD与⊙O的位置关系,并证明你的判断. (3)如果tanB=4/3,AD=x,BE=y,求y与x的函数解析式,并写出自变量x的取值范围.例6.已知等边△ABC边长为a,D、E分别为AB、AC边上的动点,且在运动时保持DE∥BC,如图(1),⊙O1与⊙O2都不在△ABC的外部,且⊙O1、⊙O2分别与∠B和∠C的两边及DE都相切,其中和DE、BC的切点分别为M、N、M′、N′.
(1)求证:⊙O1和⊙O2是等圆;(2)设⊙O1的半径长为x,圆心距O1O2为y,求y与x的函数关系式,并写出x的取值范围;(3)当⊙O1与⊙O2外切时,求x的值.
(4)如图(2),当D、E分别是AB、AC边的中点时,将⊙O2先向左平移至和⊙O1重合,然后将重合后的圆沿着△ABC内各边按图(2)中箭头的方向进行滚动,且总是与△ABC的边相切,当点O1第一次回到它原来的位置时,求点O1经过的路线长度.
同课章节目录
