人教版数学八年级下册19.3课题学习选择方案 基础练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册19.3课题学习选择方案 基础练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 08:14:18 | ||
图片预览



文档简介
19.3 课题学习 选择方案 基础练习
一、单选题
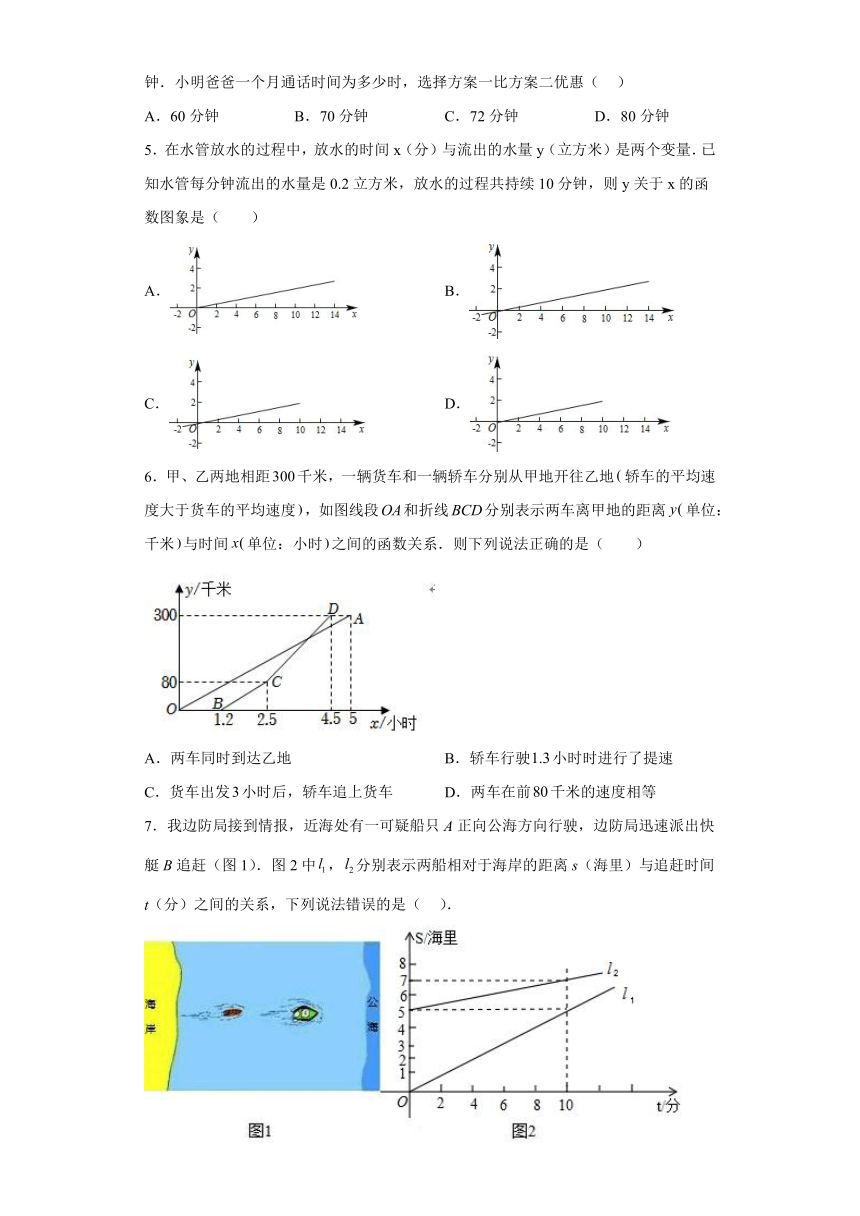
1.弹簧伸长的长度与所受拉力的大小成正比,某次实验中,小明记录了同一根弹簧的长度y(cm)和所挂重物的质量x(kg)(0≤x≤12)之间的部分对应数据如下表所示,下列说法中正确的是( )
x(kg) 0 0.5 1 1.5 2 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的正比例函数
B.当所挂重物的质量为5kg时,弹簧长度是14.5cm
C.物体质量由5kg增加到7kg,弹簧的长度增加了1cm
D.该弹簧不挂重物时的长度是10cm
2.如图,在平面直角坐标系中,已知正比例函数与一次函数的图象交于点,设轴上有一点,过点作轴的垂线(垂线位于点的右侧)分别交和的图象与点、,连接,若,则的面积为( )
A. B. C. D.
3.小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减元.若小涵购买咖啡豆公克且自备容器,需支付元;阿嘉购买咖啡豆公克但没有自备容器,需支付元,则与的关系式为下列何者?( )
A. B.
C. D.
4.联通公司推出两种手机收费方案.方案一:月租费36元,本地通话话费元/分;方案二:不收月租费,本地通话费为元/分.设小明的爸爸一个月通话时间为分钟.小明爸爸一个月通话时间为多少时,选择方案一比方案二优惠( )
A.60分钟 B.70分钟 C.72分钟 D.80分钟
5.在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程共持续10分钟,则y关于x的函数图象是( )
A. B.
C. D.
6.甲、乙两地相距千米,一辆货车和一辆轿车分别从甲地开往乙地轿车的平均速度大于货车的平均速度,如图线段和折线分别表示两车离甲地的距离单位:千米与时间单位:小时之间的函数关系.则下列说法正确的是( )
A.两车同时到达乙地 B.轿车行驶小时时进行了提速
C.货车出发小时后,轿车追上货车 D.两车在前千米的速度相等
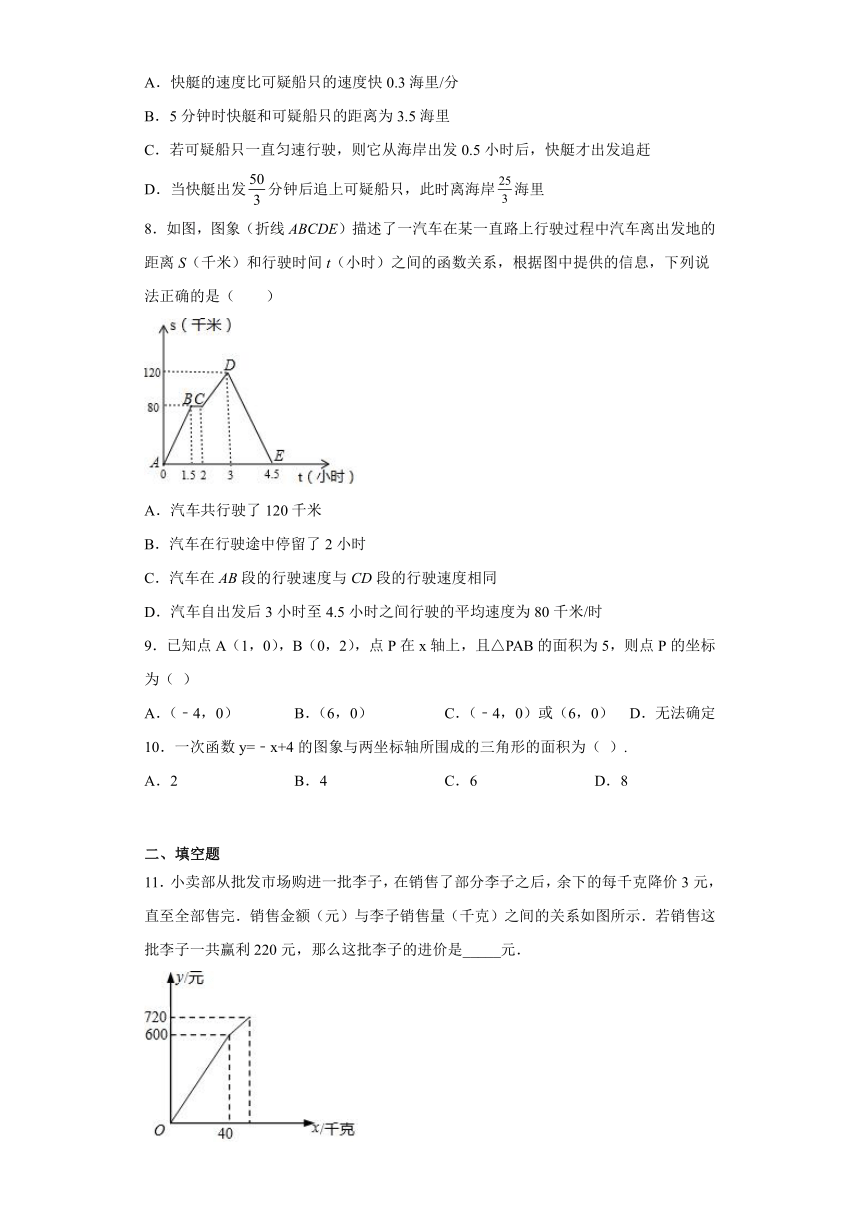
7.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中,分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系,下列说法错误的是( ).
A.快艇的速度比可疑船只的速度快0.3海里/分
B.5分钟时快艇和可疑船只的距离为3.5海里
C.若可疑船只一直匀速行驶,则它从海岸出发0.5小时后,快艇才出发追赶
D.当快艇出发分钟后追上可疑船只,此时离海岸海里
8.如图,图象(折线ABCDE)描述了一汽车在某一直路上行驶过程中汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,下列说法正确的是( )
A.汽车共行驶了120千米
B.汽车在行驶途中停留了2小时
C.汽车在AB段的行驶速度与CD段的行驶速度相同
D.汽车自出发后3小时至4.5小时之间行驶的平均速度为80千米/时
9.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为( )
A.(﹣4,0) B.(6,0) C.(﹣4,0)或(6,0) D.无法确定
10.一次函数y=﹣x+4的图象与两坐标轴所围成的三角形的面积为( ).
A.2 B.4 C.6 D.8
二、填空题
11.小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是_____元.
12.一个水库的水位在最近的小时内将持续上涨.如表记录了小时内个时间点对应的水位高度,其中表示时间,表示对应的水位高度.根据表中的数据,请写出一个关于的函数解析式合理预估水位的变化规律.该函数解析式是:______.(不写自变量取值范围)
小时
米
13.若点(m,n)在函数y=2x+1的图象上,则2m﹣n的值是_____.
14.如图,点B,C分别在直线y=2x和直线y=kx上,A、D是x轴上两点,若四边形ABCD是长方形,且AB:AD=1:3,则k的值为__________.
15.我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为__.
三、解答题
16.已知平面直角坐标系内的点A(m﹣3,2m﹣2)在第二象限,且m为整数,B(3,1).
(1)求点A的坐标;
(2)点P是x轴上一动点,当PA+PB最小时,求:①点P的坐标;②PA+PB的最小值.
17.某水果店进行了一次水果促销活动,在该店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图所示,
(1)当时,单价y为______元;当单价y为8.8元时,购买量x(千克)的取值范围为______;
(2)根据函数图象,当时,求出函数图象中单价y(元)与购买量x(千克)的函数关系式;
(3)促销活动期间,张亮计划去该店购买A种水果10千克,那么张亮共需花费多少元?
18.某公司计划十月份组织员工到外地旅游,人数在10~30人之间.甲、乙两个旅行社的服务质量相同,且价格都是每人500元.甲旅行社表示可先免去两位游客的旅游费用,其余人九折优惠,乙旅行社表示给予每位游客八折优惠.
(1)写出甲乙两个旅行社收费y与人数x之间的函数关系式.
(2)如果你是这次出游的组织者,当去多少人时两家旅行社的总费用相同.
(3)当去17人时,选哪家旅行社更优惠?请说明理由.
19.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=_________分钟时甲乙两人相遇,甲的速度为__________米/分钟;
(2)求出线段AB所表示的函数表达式,并写出自变量的范围.
20.张伯伯家专业种植狗头枣,他利用直播销售方式把狗头枣远销全国各地.对狗头枣出售价格根据购买量给予优惠,设顾客一次性购买狗头枣,付款元,与之间的函数关系如图所示.
(1)求与之间的函数关系式;
(2)某位顾客通过直播在张伯伯家一次性购买狗头枣共花费870元,这位顾客共购买了多少千克狗头枣?
参考答案
1.D
2.A
3.D
4.D
5.D
6.B
7.C
8.D
9.C
10.D
11.10
12./y=0.2t+3
13.﹣1
14.
15.3.
16.解:(1)∵点A(m﹣3,2m﹣2)在第二象限,且m为整数,
∴,
解得1<m<3,
∴m=2,
∴A(﹣1,2);
(2)如图,作点A关于x轴的对称点C,则C(﹣1,﹣2),
连接BC交x轴于P,设直线BC的解析式为y=kx+b,则
,
解得,
∴y=x﹣;
①令y=0,则x=,即P(,0);
②如图,过C作CD∥x轴,过B作BD∥y轴,则CD=4,BD=3,
∴Rt△BCD中,BC==5,
即PA+PB的最小值为5.
17.解:(1)观察函数图象的横坐标,纵坐标,不超过5千克时,单价是10元,数量不少于11千克时,单价为8.8元.
故答案为:10;;
(2)设函数图象的解析式 (k是常数,b是常数,),
图象过点,,
可得:,
解得,
函数图象的解析式:;
(3)当时,
,
答:促销活动期间,去该店购买A种水果10千克,那么共需花费9元.
18.解:(1)由题意得,
甲旅行社费用y与人数x之间的函数表达式:y=500×(x-2)×0.9=450x-900;
乙旅行社费用y与人数x之间的函数表达式:y=500x×0.8=400x,
故答案为,;
(2)设当人数是x人时,两家旅行社的总费用相同,由题意得:
500x×0.8=500×(x-2)×0.9
400x=450x-900
50x=900
x=18
答:当人数是18人时,两个旅行社旅游费用一样多;
(3)当x=17时,
甲旅行社费用:450×17-900=6750元;
乙旅行社费用:400×17=6800元;
6750<6800,
甲旅行社费用少些;
答:当去17人时,选甲旅行社更优惠.
19.解:(1)根据图象信息,当t=24分钟时甲乙两人相遇,
甲的速度为2400÷60=40米/分钟.
(2)∵甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,t=24分钟时甲乙两人相遇,
∴甲、乙两人的速度和为2400÷24=100米/分钟,
∵甲的速度为40米/分钟
∴乙的速度为100﹣40=60米/分钟.
∴乙从图书馆回学校的时间为2400÷60=40分钟,
此时甲乙的距离为100×(40-24)=1600,
即甲、乙此时相距1600米
∴A点的坐标为(40,1600).
设线段AB所表示的函数表达式为y=kt+b,
∵A(40,1600),B(60,2400),
∴ ,解得 .
∴线段AB所表示的函数表达式为y=40t(40≤t≤60).
20. (1)解:由题意可知,①当0≤x≤10时,设与之间的函数关系式为:y=kx,图像过点(10,600),
即10k=600,
解得:k=60,
则当0≤x≤10时,设与之间的函数关系式为:y=60x,
②当x>10时,设与之间的函数关系式为:y=mx+n(m≠0),代入点(10,600),(20,1140),
得:,
解得:,
即,当x>10时,设与之间的函数关系式为:y=54x+60,
综上所述,y与x的函数关系式为:y=;
(2)∵870>600,
∴令y=54x+60=870,
解得:x=15.
即这位顾客共购买了15千克狗头枣.
一、单选题
1.弹簧伸长的长度与所受拉力的大小成正比,某次实验中,小明记录了同一根弹簧的长度y(cm)和所挂重物的质量x(kg)(0≤x≤12)之间的部分对应数据如下表所示,下列说法中正确的是( )
x(kg) 0 0.5 1 1.5 2 …
y(cm) 10.5 11 11.5 12 …
A.x,y都是变量,y是x的正比例函数
B.当所挂重物的质量为5kg时,弹簧长度是14.5cm
C.物体质量由5kg增加到7kg,弹簧的长度增加了1cm
D.该弹簧不挂重物时的长度是10cm
2.如图,在平面直角坐标系中,已知正比例函数与一次函数的图象交于点,设轴上有一点,过点作轴的垂线(垂线位于点的右侧)分别交和的图象与点、,连接,若,则的面积为( )
A. B. C. D.
3.小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减元.若小涵购买咖啡豆公克且自备容器,需支付元;阿嘉购买咖啡豆公克但没有自备容器,需支付元,则与的关系式为下列何者?( )
A. B.
C. D.
4.联通公司推出两种手机收费方案.方案一:月租费36元,本地通话话费元/分;方案二:不收月租费,本地通话费为元/分.设小明的爸爸一个月通话时间为分钟.小明爸爸一个月通话时间为多少时,选择方案一比方案二优惠( )
A.60分钟 B.70分钟 C.72分钟 D.80分钟
5.在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程共持续10分钟,则y关于x的函数图象是( )
A. B.
C. D.
6.甲、乙两地相距千米,一辆货车和一辆轿车分别从甲地开往乙地轿车的平均速度大于货车的平均速度,如图线段和折线分别表示两车离甲地的距离单位:千米与时间单位:小时之间的函数关系.则下列说法正确的是( )
A.两车同时到达乙地 B.轿车行驶小时时进行了提速
C.货车出发小时后,轿车追上货车 D.两车在前千米的速度相等
7.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶(图1).图2中,分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系,下列说法错误的是( ).
A.快艇的速度比可疑船只的速度快0.3海里/分
B.5分钟时快艇和可疑船只的距离为3.5海里
C.若可疑船只一直匀速行驶,则它从海岸出发0.5小时后,快艇才出发追赶
D.当快艇出发分钟后追上可疑船只,此时离海岸海里
8.如图,图象(折线ABCDE)描述了一汽车在某一直路上行驶过程中汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,下列说法正确的是( )
A.汽车共行驶了120千米
B.汽车在行驶途中停留了2小时
C.汽车在AB段的行驶速度与CD段的行驶速度相同
D.汽车自出发后3小时至4.5小时之间行驶的平均速度为80千米/时
9.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为( )
A.(﹣4,0) B.(6,0) C.(﹣4,0)或(6,0) D.无法确定
10.一次函数y=﹣x+4的图象与两坐标轴所围成的三角形的面积为( ).
A.2 B.4 C.6 D.8
二、填空题
11.小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是_____元.
12.一个水库的水位在最近的小时内将持续上涨.如表记录了小时内个时间点对应的水位高度,其中表示时间,表示对应的水位高度.根据表中的数据,请写出一个关于的函数解析式合理预估水位的变化规律.该函数解析式是:______.(不写自变量取值范围)
小时
米
13.若点(m,n)在函数y=2x+1的图象上,则2m﹣n的值是_____.
14.如图,点B,C分别在直线y=2x和直线y=kx上,A、D是x轴上两点,若四边形ABCD是长方形,且AB:AD=1:3,则k的值为__________.
15.我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为__.
三、解答题
16.已知平面直角坐标系内的点A(m﹣3,2m﹣2)在第二象限,且m为整数,B(3,1).
(1)求点A的坐标;
(2)点P是x轴上一动点,当PA+PB最小时,求:①点P的坐标;②PA+PB的最小值.
17.某水果店进行了一次水果促销活动,在该店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图所示,
(1)当时,单价y为______元;当单价y为8.8元时,购买量x(千克)的取值范围为______;
(2)根据函数图象,当时,求出函数图象中单价y(元)与购买量x(千克)的函数关系式;
(3)促销活动期间,张亮计划去该店购买A种水果10千克,那么张亮共需花费多少元?
18.某公司计划十月份组织员工到外地旅游,人数在10~30人之间.甲、乙两个旅行社的服务质量相同,且价格都是每人500元.甲旅行社表示可先免去两位游客的旅游费用,其余人九折优惠,乙旅行社表示给予每位游客八折优惠.
(1)写出甲乙两个旅行社收费y与人数x之间的函数关系式.
(2)如果你是这次出游的组织者,当去多少人时两家旅行社的总费用相同.
(3)当去17人时,选哪家旅行社更优惠?请说明理由.
19.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=_________分钟时甲乙两人相遇,甲的速度为__________米/分钟;
(2)求出线段AB所表示的函数表达式,并写出自变量的范围.
20.张伯伯家专业种植狗头枣,他利用直播销售方式把狗头枣远销全国各地.对狗头枣出售价格根据购买量给予优惠,设顾客一次性购买狗头枣,付款元,与之间的函数关系如图所示.
(1)求与之间的函数关系式;
(2)某位顾客通过直播在张伯伯家一次性购买狗头枣共花费870元,这位顾客共购买了多少千克狗头枣?
参考答案
1.D
2.A
3.D
4.D
5.D
6.B
7.C
8.D
9.C
10.D
11.10
12./y=0.2t+3
13.﹣1
14.
15.3.
16.解:(1)∵点A(m﹣3,2m﹣2)在第二象限,且m为整数,
∴,
解得1<m<3,
∴m=2,
∴A(﹣1,2);
(2)如图,作点A关于x轴的对称点C,则C(﹣1,﹣2),
连接BC交x轴于P,设直线BC的解析式为y=kx+b,则
,
解得,
∴y=x﹣;
①令y=0,则x=,即P(,0);
②如图,过C作CD∥x轴,过B作BD∥y轴,则CD=4,BD=3,
∴Rt△BCD中,BC==5,
即PA+PB的最小值为5.
17.解:(1)观察函数图象的横坐标,纵坐标,不超过5千克时,单价是10元,数量不少于11千克时,单价为8.8元.
故答案为:10;;
(2)设函数图象的解析式 (k是常数,b是常数,),
图象过点,,
可得:,
解得,
函数图象的解析式:;
(3)当时,
,
答:促销活动期间,去该店购买A种水果10千克,那么共需花费9元.
18.解:(1)由题意得,
甲旅行社费用y与人数x之间的函数表达式:y=500×(x-2)×0.9=450x-900;
乙旅行社费用y与人数x之间的函数表达式:y=500x×0.8=400x,
故答案为,;
(2)设当人数是x人时,两家旅行社的总费用相同,由题意得:
500x×0.8=500×(x-2)×0.9
400x=450x-900
50x=900
x=18
答:当人数是18人时,两个旅行社旅游费用一样多;
(3)当x=17时,
甲旅行社费用:450×17-900=6750元;
乙旅行社费用:400×17=6800元;
6750<6800,
甲旅行社费用少些;
答:当去17人时,选甲旅行社更优惠.
19.解:(1)根据图象信息,当t=24分钟时甲乙两人相遇,
甲的速度为2400÷60=40米/分钟.
(2)∵甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,t=24分钟时甲乙两人相遇,
∴甲、乙两人的速度和为2400÷24=100米/分钟,
∵甲的速度为40米/分钟
∴乙的速度为100﹣40=60米/分钟.
∴乙从图书馆回学校的时间为2400÷60=40分钟,
此时甲乙的距离为100×(40-24)=1600,
即甲、乙此时相距1600米
∴A点的坐标为(40,1600).
设线段AB所表示的函数表达式为y=kt+b,
∵A(40,1600),B(60,2400),
∴ ,解得 .
∴线段AB所表示的函数表达式为y=40t(40≤t≤60).
20. (1)解:由题意可知,①当0≤x≤10时,设与之间的函数关系式为:y=kx,图像过点(10,600),
即10k=600,
解得:k=60,
则当0≤x≤10时,设与之间的函数关系式为:y=60x,
②当x>10时,设与之间的函数关系式为:y=mx+n(m≠0),代入点(10,600),(20,1140),
得:,
解得:,
即,当x>10时,设与之间的函数关系式为:y=54x+60,
综上所述,y与x的函数关系式为:y=;
(2)∵870>600,
∴令y=54x+60=870,
解得:x=15.
即这位顾客共购买了15千克狗头枣.
