18.2.2 矩形——矩形的性质课件 2022—2023学年人教版数学八年级下册 18张PPT
文档属性
| 名称 | 18.2.2 矩形——矩形的性质课件 2022—2023学年人教版数学八年级下册 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 149.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 09:00:49 | ||
图片预览





文档简介
(共18张PPT)
矩形的性质
第十八章 平行四边形
活动:利用几何画板的平行四边形进行演示,使平行四边形的一个内角变化,请同学们注意观察.
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
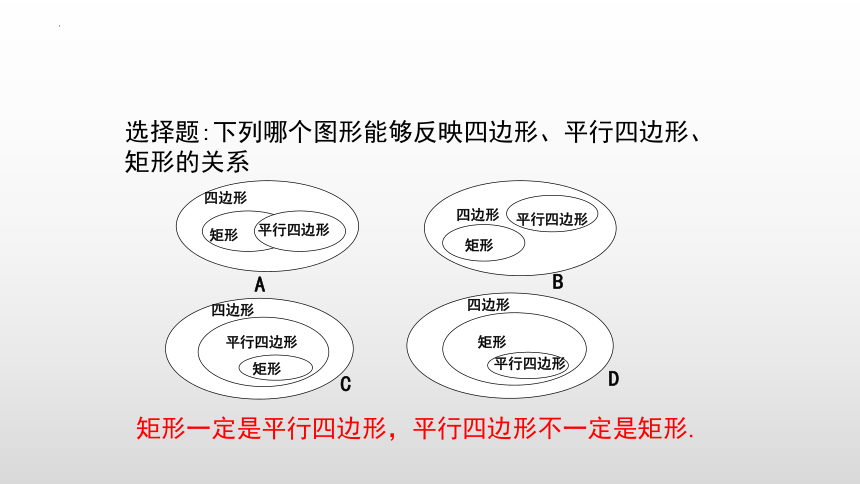
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
矩形一定是平行四边形,平行四边形不一定是矩形.
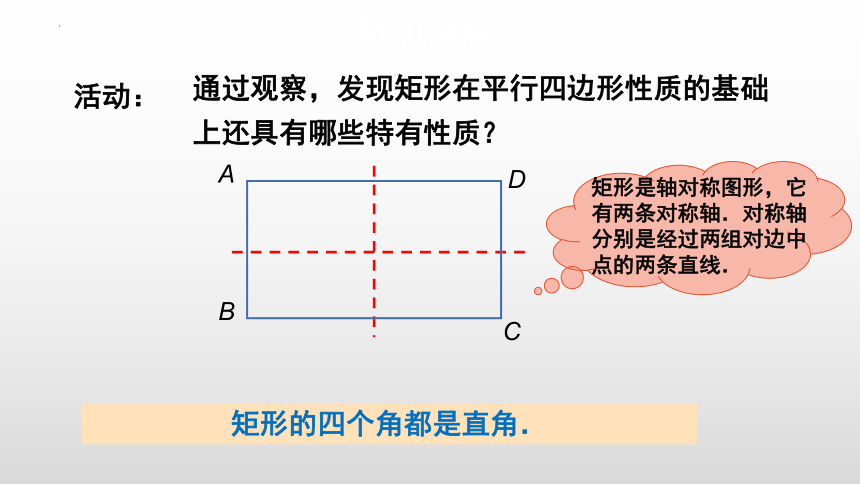
活动:
通过观察,发现矩形在平行四边形性质的基础上还具有哪些特有性质?
矩形的四个角都是直角.
矩形是轴对称图形,它有两条对称轴.对称轴分别是经过两组对边中点的两条直线.
新知讲解
A
D
C
B
求证:矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°.
求证:∠A= ∠B= ∠C=∠D=90°.
新知讲解
证明:∵四边形ABCD是矩形,
∴ ∠C=∠A=90°,∠D=∠B,AD∥BC.
∴ ∠A+ ∠B=180°,
∴ ∠D=∠B=180°-∠A
=180°- 90°=90°,
即矩形的四个角都是直角.
A
B
C
D
新知讲解
结论:
矩形的性质定理 矩形的四个角都是直角.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
新知讲解
活动:
观察图形的变化. 你发现了什么?
矩形的对角线相等.
新知讲解
求证:矩形的对角线相等.
已知:四边形ABCD是矩形.求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD,
即矩形的对角线相等.
新知讲解
结论:
矩形的性质定理 矩形的对角线相等.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴AC = BD.
新知讲解
设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系 为什么
D
B
C
A
E
由此可得推论:
直角三角形斜边上的中线等于斜边的一半
BE是Rt△ABC中斜边AC上的中线.
BE等于AC的一半.
∵ AC=BD,BE=DE,
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝),
∴ 矩形的对角线长 AC=BD=2OA=8(㎝).
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
2. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )
1. 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
D
D
基础训练
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于 ( )
A.30° B.45° C.60° D.120°
D
A
5. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm).
即矩形ABCD的周长等于34cm.
A D
B C
O
6. 在矩形ABCD中,对角线AC,BD相交于点O,
若∠AOB=60°,AC=10,则AB=________.
7. 如图,矩形ABCD中,AC,BD交于点O,
M,N分别为BC,OC的中点.若MN=4,则AC
的长为__________.
5
16
8.如图,在△ABC中,AB=10,BC=8,
AD垂直平分BC,垂足为D,点E是AC的中
点,连接DE,则△CDE的周长为_________.
9.(上海)如图,已知直线l1∥l2,含30°
角的三角板的直角顶点C在l1上,30°角的
顶点A在l2上,如果边AB与l1的交点D是AB
的中点,那么∠1=__________度.
14
120
矩形的性质
第十八章 平行四边形
活动:利用几何画板的平行四边形进行演示,使平行四边形的一个内角变化,请同学们注意观察.
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形.
也叫做长方形.
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
矩形一定是平行四边形,平行四边形不一定是矩形.
活动:
通过观察,发现矩形在平行四边形性质的基础上还具有哪些特有性质?
矩形的四个角都是直角.
矩形是轴对称图形,它有两条对称轴.对称轴分别是经过两组对边中点的两条直线.
新知讲解
A
D
C
B
求证:矩形的四个角都是直角.
A
B
C
D
已知:如图,四边形ABCD是矩形,且∠A=90°.
求证:∠A= ∠B= ∠C=∠D=90°.
新知讲解
证明:∵四边形ABCD是矩形,
∴ ∠C=∠A=90°,∠D=∠B,AD∥BC.
∴ ∠A+ ∠B=180°,
∴ ∠D=∠B=180°-∠A
=180°- 90°=90°,
即矩形的四个角都是直角.
A
B
C
D
新知讲解
结论:
矩形的性质定理 矩形的四个角都是直角.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°.
新知讲解
活动:
观察图形的变化. 你发现了什么?
矩形的对角线相等.
新知讲解
求证:矩形的对角线相等.
已知:四边形ABCD是矩形.求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
AB = DC , BC = CB,
∴△ABC≌△DCB,
∴AC = BD,
即矩形的对角线相等.
新知讲解
结论:
矩形的性质定理 矩形的对角线相等.
A
B
C
D
符号语言:
∵四边形ABCD是矩形,
∴AC = BD.
新知讲解
设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段
它与AC有什么大小关系 为什么
D
B
C
A
E
由此可得推论:
直角三角形斜边上的中线等于斜边的一半
BE是Rt△ABC中斜边AC上的中线.
BE等于AC的一半.
∵ AC=BD,BE=DE,
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝),
∴ 矩形的对角线长 AC=BD=2OA=8(㎝).
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
2. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )
1. 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
D
D
基础训练
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于 ( )
A.30° B.45° C.60° D.120°
D
A
5. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm).
即矩形ABCD的周长等于34cm.
A D
B C
O
6. 在矩形ABCD中,对角线AC,BD相交于点O,
若∠AOB=60°,AC=10,则AB=________.
7. 如图,矩形ABCD中,AC,BD交于点O,
M,N分别为BC,OC的中点.若MN=4,则AC
的长为__________.
5
16
8.如图,在△ABC中,AB=10,BC=8,
AD垂直平分BC,垂足为D,点E是AC的中
点,连接DE,则△CDE的周长为_________.
9.(上海)如图,已知直线l1∥l2,含30°
角的三角板的直角顶点C在l1上,30°角的
顶点A在l2上,如果边AB与l1的交点D是AB
的中点,那么∠1=__________度.
14
120
