2022—2023学年人教版数学八年级下册 18.2.1 形中的折叠问题 说课课件(共19张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册 18.2.1 形中的折叠问题 说课课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 09:13:15 | ||
图片预览





文档简介
(共19张PPT)
第十八章 小结(2)
矩形中的折叠问题
人教版2011课标版《数学》八年级下册
说 课 内 容
二、学 情 分 析
三、 教 学 目 标
四、 教法与学法
五、 教 学 过 程
一、 教 材 分 析
一、教 材 分 析
矩形中的折叠问题在初中数学中虽然没有编入课本,但折叠融入了对称思想,综合了三角形、四边形的诸多知识,变化灵活,趣味性强。折纸活动本身也承载着许多重要的几何问题,在梳理了特殊四边形的性质后,进行《矩形中的折叠》的专题复习,能提炼一般的几何学习方法,对于培养学生的学习兴趣与探索精神,有非常重要的价值。
二、学 情 分 析
该该年龄段的学生爱操作,爱思考,爱表达,想通过自己的努力获得成功。知识上,经过八年级的学习,掌握了折叠相关的轴对称、等腰三角形、直角三角形,以及特殊平行四边形的性质和判定,已具备对简单图形的识别判断和说理能力。但相当一部分学生的数学思维缺乏条理,对稍微复杂图形的分析转化能力比较薄弱,综合分析的能力有待提高。
(1)通过学习,掌握矩形中的折叠问题的解题规律。
(2)通过操作、观察、猜想、验证、归纳等方法进一步提高综合解决问题的能力。
(3)学习如何把问题归类,形成发现解题规律的能力。
(4)通过综合应用数学知识解决折叠问题,体会知识间的联系,感受数学学习的乐趣.
三、教学目标
为帮助学生揭示解题规律,总结解题方法,进一步提高运用所学知识分析问题、解决问题的能力;
首先精选例题:
(1)具有典型性,通过一例一题发掘尽可能多的利用资源;
(2)具有针对性,符合学生学情,太易,学生一看就知道答案,复习只能停留在表面,缺乏深入的思考;太难则又让课堂显得沉闷、乏味。
(3)具有变化性,题型丰富。在变化中寻找规律,在丰富中体会乐趣.
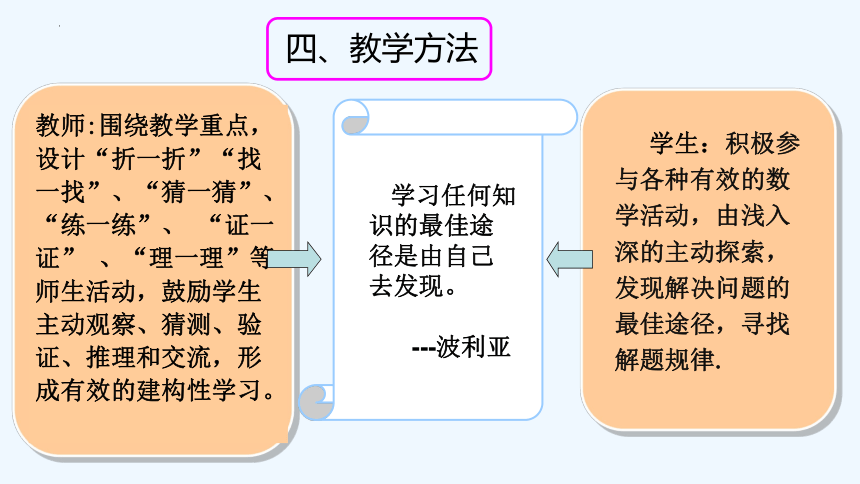
教师:围绕教学重点,设计“折一折”“找一找”、“猜一猜”、“练一练”、 “证一证” 、“理一理”等师生活动,鼓励学生主动观察、猜测、验证、推理和交流,形成有效的建构性学习。
四、教学方法
学生:积极参与各种有效的数学活动,由浅入深的主动探索,发现解决问题的最佳途径,寻找解题规律.
学习任何知识的最佳途径是由自己去发现。
---波利亚
五、教 学 过 程
活动引入 课题准备
自主探究 合作交流
课堂小结 归纳反思
独立应用 能力延伸
忆一忆
1:如图矩形ABCD,你能说说它有哪些性质?
边:AB=CD , BC=AD
AB∥CD, BC∥AD
角:∠BAD=∠ABC=∠BCD=∠CDA=90°
对角线:OA=OB=OC=OD
设计意图:引导学生有条理回顾概念及相关性质,为后面研究学习做准备。
活动规则:把手中的矩形纸片折叠一次。
②从几何学习的角度,你对折叠后的哪个图形最感兴趣?
①你想一想矩形纸片相同,折叠规则相同,为什么折叠生成了不同的图形?
折一折
设计意图:折,感受矩形折叠生成的丰富图形,培养学生对几何图形的直观感知。折后追问,引导对矩形纸片折叠的观察,养成良好的思考习惯,要善于思考,善于发现,增强学生学习数学的兴趣,调动学生学习的积极性和主动性。
折叠问题因为有了“折”就有了“形”----轴对称图形、全等形;有了“折”就有了“数”----线段之间、角与角之间的数量关系。“折”就为“数”与“形”之间的转化搭起了桥梁。本节课研究的就是矩形折叠中的以下三个典型图形。
理一理
对照表格,反思问题1的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
全等形
直角三角形
“ K”型
数形结合
勾股定理
方程思想
建模思想
设计意图:折痕的变化,引导学生寻找相应的新特点,以此培养学生的观察能力和归纳能力,使学生感受到数学学习是有趣的、丰富的、有价值的.
理一理
对照表格,反思问题2的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
①关注图中的等线段,等角,直角;
②角平分线遇平行线时出现的等腰三角形。
等腰三角形
直角三角形
勾股定理
方程思想
设计意图:层层递进,问题3既是前面总结的知识与解题方法的运用,又是折痕变化新特点的再次探究,既是重点,也是难点。一题多解,开阔学生思路,训练思维的发散性、灵活性,充分体现由未知转化为已知的数学思想。
理一理
对照表格,反思问题3的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
①关注图中的等线段,等角,直角;
②角平分线遇平行线时出现的等腰三角形;
③对称点的连线被对称轴垂直平分;
等腰三角形
直角三角形
“X”型
菱形
数形结合
转化思想方程思想勾股定理
等面积法
对照下面几个问题谈谈你的想法:
(1)这节课学到了什么?
(2)本节课的问题解决主要采用了什么方法?
(3)还有那些疑问?
说一说
矩形中的折叠
设计意图:引导梳理学习内容,帮助学生养成整理知识的习惯。同时养成反思学习过程的习惯,为后续的学习做好铺垫。
如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)△MNK的面积能否小于 若能,求出此时∠1的度数;若不能,试说明理由;
(2)如何折叠能够使△MNK的面积最大 请你用备用图探究可能出现的情况,求最大值。
能力延伸
设计意图:既是对本节课的检测,又是能力拓展延伸。举一反三,让学生运用学会的方法和思路独立解决问题,形成触类旁通的数学能力。
第十八章 小结(2)
矩形中的折叠问题
人教版2011课标版《数学》八年级下册
说 课 内 容
二、学 情 分 析
三、 教 学 目 标
四、 教法与学法
五、 教 学 过 程
一、 教 材 分 析
一、教 材 分 析
矩形中的折叠问题在初中数学中虽然没有编入课本,但折叠融入了对称思想,综合了三角形、四边形的诸多知识,变化灵活,趣味性强。折纸活动本身也承载着许多重要的几何问题,在梳理了特殊四边形的性质后,进行《矩形中的折叠》的专题复习,能提炼一般的几何学习方法,对于培养学生的学习兴趣与探索精神,有非常重要的价值。
二、学 情 分 析
该该年龄段的学生爱操作,爱思考,爱表达,想通过自己的努力获得成功。知识上,经过八年级的学习,掌握了折叠相关的轴对称、等腰三角形、直角三角形,以及特殊平行四边形的性质和判定,已具备对简单图形的识别判断和说理能力。但相当一部分学生的数学思维缺乏条理,对稍微复杂图形的分析转化能力比较薄弱,综合分析的能力有待提高。
(1)通过学习,掌握矩形中的折叠问题的解题规律。
(2)通过操作、观察、猜想、验证、归纳等方法进一步提高综合解决问题的能力。
(3)学习如何把问题归类,形成发现解题规律的能力。
(4)通过综合应用数学知识解决折叠问题,体会知识间的联系,感受数学学习的乐趣.
三、教学目标
为帮助学生揭示解题规律,总结解题方法,进一步提高运用所学知识分析问题、解决问题的能力;
首先精选例题:
(1)具有典型性,通过一例一题发掘尽可能多的利用资源;
(2)具有针对性,符合学生学情,太易,学生一看就知道答案,复习只能停留在表面,缺乏深入的思考;太难则又让课堂显得沉闷、乏味。
(3)具有变化性,题型丰富。在变化中寻找规律,在丰富中体会乐趣.
教师:围绕教学重点,设计“折一折”“找一找”、“猜一猜”、“练一练”、 “证一证” 、“理一理”等师生活动,鼓励学生主动观察、猜测、验证、推理和交流,形成有效的建构性学习。
四、教学方法
学生:积极参与各种有效的数学活动,由浅入深的主动探索,发现解决问题的最佳途径,寻找解题规律.
学习任何知识的最佳途径是由自己去发现。
---波利亚
五、教 学 过 程
活动引入 课题准备
自主探究 合作交流
课堂小结 归纳反思
独立应用 能力延伸
忆一忆
1:如图矩形ABCD,你能说说它有哪些性质?
边:AB=CD , BC=AD
AB∥CD, BC∥AD
角:∠BAD=∠ABC=∠BCD=∠CDA=90°
对角线:OA=OB=OC=OD
设计意图:引导学生有条理回顾概念及相关性质,为后面研究学习做准备。
活动规则:把手中的矩形纸片折叠一次。
②从几何学习的角度,你对折叠后的哪个图形最感兴趣?
①你想一想矩形纸片相同,折叠规则相同,为什么折叠生成了不同的图形?
折一折
设计意图:折,感受矩形折叠生成的丰富图形,培养学生对几何图形的直观感知。折后追问,引导对矩形纸片折叠的观察,养成良好的思考习惯,要善于思考,善于发现,增强学生学习数学的兴趣,调动学生学习的积极性和主动性。
折叠问题因为有了“折”就有了“形”----轴对称图形、全等形;有了“折”就有了“数”----线段之间、角与角之间的数量关系。“折”就为“数”与“形”之间的转化搭起了桥梁。本节课研究的就是矩形折叠中的以下三个典型图形。
理一理
对照表格,反思问题1的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
全等形
直角三角形
“ K”型
数形结合
勾股定理
方程思想
建模思想
设计意图:折痕的变化,引导学生寻找相应的新特点,以此培养学生的观察能力和归纳能力,使学生感受到数学学习是有趣的、丰富的、有价值的.
理一理
对照表格,反思问题2的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
①关注图中的等线段,等角,直角;
②角平分线遇平行线时出现的等腰三角形。
等腰三角形
直角三角形
勾股定理
方程思想
设计意图:层层递进,问题3既是前面总结的知识与解题方法的运用,又是折痕变化新特点的再次探究,既是重点,也是难点。一题多解,开阔学生思路,训练思维的发散性、灵活性,充分体现由未知转化为已知的数学思想。
理一理
对照表格,反思问题3的解题过程,你从中领悟到了什么?
相关的知识点 涉及的基本图形 解题思想方法
①关注图中的等线段,等角,直角;
②角平分线遇平行线时出现的等腰三角形;
③对称点的连线被对称轴垂直平分;
等腰三角形
直角三角形
“X”型
菱形
数形结合
转化思想方程思想勾股定理
等面积法
对照下面几个问题谈谈你的想法:
(1)这节课学到了什么?
(2)本节课的问题解决主要采用了什么方法?
(3)还有那些疑问?
说一说
矩形中的折叠
设计意图:引导梳理学习内容,帮助学生养成整理知识的习惯。同时养成反思学习过程的习惯,为后续的学习做好铺垫。
如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)△MNK的面积能否小于 若能,求出此时∠1的度数;若不能,试说明理由;
(2)如何折叠能够使△MNK的面积最大 请你用备用图探究可能出现的情况,求最大值。
能力延伸
设计意图:既是对本节课的检测,又是能力拓展延伸。举一反三,让学生运用学会的方法和思路独立解决问题,形成触类旁通的数学能力。
