18.2.3 正方形 课件 2022—2023学年人教版数学八年级下册 15张PPT
文档属性
| 名称 | 18.2.3 正方形 课件 2022—2023学年人教版数学八年级下册 15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 09:09:28 | ||
图片预览




文档简介
(共15张PPT)
第十八章 平行四边形
正方形
教学目标
1.正方形性质和判定定理的应用 ,(重点)
2.正方形与平行四边形、矩形、菱形的区别与联系 .(难点)
新课导入
八年级(2)班的简兰同学想买一条方纱巾 . 有一天她在商店里看到一块漂亮的纱巾 , 非常想买 , 但她拿起来看时感觉纱巾不太方 , 商店老板看她犹豫不决的样子 , 马上过来拉起一组对角 , 让她看另一组对角是否对齐 , 她还有些疑惑 , 老板又拉起另一组对角让她检验 , 她终于买下这块纱巾 , 你认为她买的这块纱巾是正方形的吗 当时采用什么方法可以检验出来
创设情景
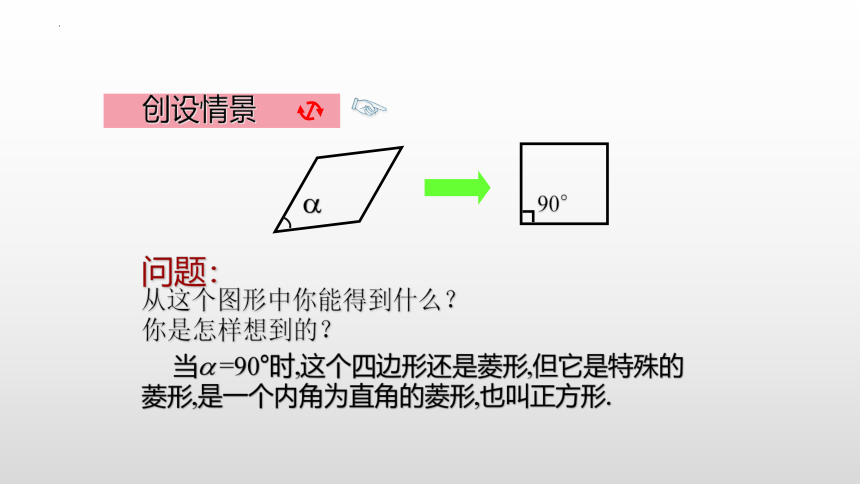
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
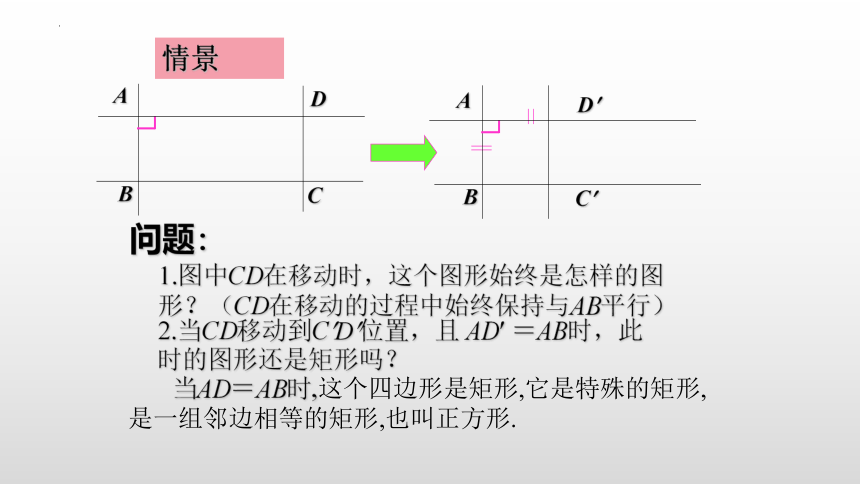
情景
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此
时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
E
A
B
C
D
F
N
M
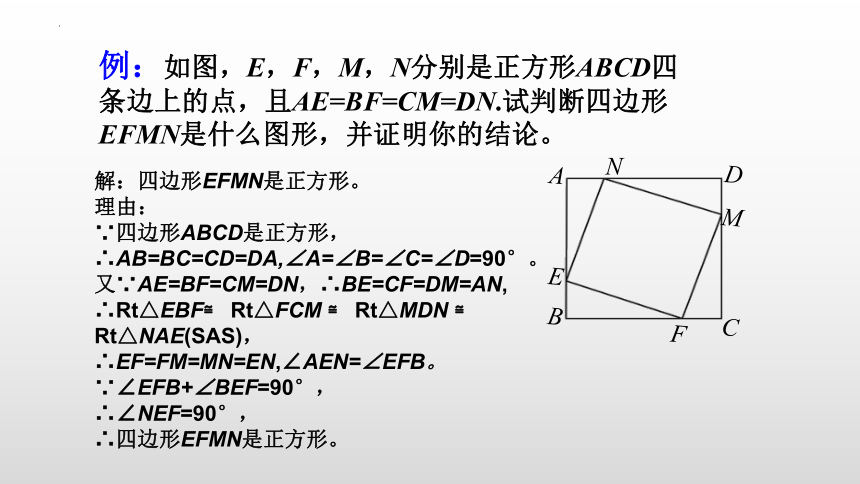
例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
定理: 有一个角是直角的菱形是正方形 .
求证 : 四边形ABCD是正方形 .
证明 :
∴ AB=BC , ∠C=∠A=90°, ∠B=180°-∠A=90°.
∴ ∠A=∠B=∠C=90°.
∴ 四边形ABCD是矩形 .
∵四边形ABCD是菱形 , ∠A=90°,
∵ AB=BC ,
∴ 四边形ABCD是正方形 .
已知 : 四边形ABCD是菱形 , ∠A=90°.
A
B
C
D
有一个角是直角的菱形是正方形 .
定理 : 对角线相等的菱形是正方形 .
求证 : 四边形ABCD是正方形 .
证明 :
∴ AB=BC , 四边形ABCD是平行四边形 .
∵ AC=BD ,
∴ 四边形ABCD是矩形 .
∵ AB=BC ,
∵ 四边形ABCD是菱形 ,
∴ 四边形ABCD是正方形 .
已知 : 四边形ABCD是菱形 , 且对角线 AC=BD .
A
B
C
D
O
对角线相等的菱形是正方形 .
随堂训练
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °
D
12cm
112.5 °
4.如图 , ABCD是一块正方形场地 . 小华和小芳在AB边上取定了一点E ,
测量知 ,EC=30m , EB=10m . 这块场地的面积和对角线分别是多少
解:根据勾股定理:
BC2=EC2-EB2
=302-102
=800 .
∴BC= ,
∴这块场地的面积= =800(m2),
对角线= =40(m) .
5.已知:如图 , △ABC中 , ∠C=90° , CD平分
∠ACB ,DE⊥BC于E , DF⊥AC于F .
求证:四边形CFDE是正方形 .
证明:∵∠C=90° , DE⊥BC于E , DF⊥AC于F ,
∴四边形CEDF有三个直角 , 它是矩形 .
又∵CD平分∠ACB ,
根据角平分线上的点都两边的距离相等 ,
可知DE=DF ,
所以矩形CEDF有一组邻边相等 .
根据正方形的判定方法 ,
知四边形CEDF是正方形 .
课堂小结
正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等,邻角分别互补
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形的判定
四条边都相等
第十八章 平行四边形
正方形
教学目标
1.正方形性质和判定定理的应用 ,(重点)
2.正方形与平行四边形、矩形、菱形的区别与联系 .(难点)
新课导入
八年级(2)班的简兰同学想买一条方纱巾 . 有一天她在商店里看到一块漂亮的纱巾 , 非常想买 , 但她拿起来看时感觉纱巾不太方 , 商店老板看她犹豫不决的样子 , 马上过来拉起一组对角 , 让她看另一组对角是否对齐 , 她还有些疑惑 , 老板又拉起另一组对角让她检验 , 她终于买下这块纱巾 , 你认为她买的这块纱巾是正方形的吗 当时采用什么方法可以检验出来
创设情景
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
情景
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此
时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
E
A
B
C
D
F
N
M
例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
定理: 有一个角是直角的菱形是正方形 .
求证 : 四边形ABCD是正方形 .
证明 :
∴ AB=BC , ∠C=∠A=90°, ∠B=180°-∠A=90°.
∴ ∠A=∠B=∠C=90°.
∴ 四边形ABCD是矩形 .
∵四边形ABCD是菱形 , ∠A=90°,
∵ AB=BC ,
∴ 四边形ABCD是正方形 .
已知 : 四边形ABCD是菱形 , ∠A=90°.
A
B
C
D
有一个角是直角的菱形是正方形 .
定理 : 对角线相等的菱形是正方形 .
求证 : 四边形ABCD是正方形 .
证明 :
∴ AB=BC , 四边形ABCD是平行四边形 .
∵ AC=BD ,
∴ 四边形ABCD是矩形 .
∵ AB=BC ,
∵ 四边形ABCD是菱形 ,
∴ 四边形ABCD是正方形 .
已知 : 四边形ABCD是菱形 , 且对角线 AC=BD .
A
B
C
D
O
对角线相等的菱形是正方形 .
随堂训练
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °
D
12cm
112.5 °
4.如图 , ABCD是一块正方形场地 . 小华和小芳在AB边上取定了一点E ,
测量知 ,EC=30m , EB=10m . 这块场地的面积和对角线分别是多少
解:根据勾股定理:
BC2=EC2-EB2
=302-102
=800 .
∴BC= ,
∴这块场地的面积= =800(m2),
对角线= =40(m) .
5.已知:如图 , △ABC中 , ∠C=90° , CD平分
∠ACB ,DE⊥BC于E , DF⊥AC于F .
求证:四边形CFDE是正方形 .
证明:∵∠C=90° , DE⊥BC于E , DF⊥AC于F ,
∴四边形CEDF有三个直角 , 它是矩形 .
又∵CD平分∠ACB ,
根据角平分线上的点都两边的距离相等 ,
可知DE=DF ,
所以矩形CEDF有一组邻边相等 .
根据正方形的判定方法 ,
知四边形CEDF是正方形 .
课堂小结
正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等,邻角分别互补
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形的判定
四条边都相等
