2023届陕西省高三下学期4月考前冲刺训练数学试题(含答案)
文档属性
| 名称 | 2023届陕西省高三下学期4月考前冲刺训练数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 412.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 20:17:39 | ||
图片预览




文档简介
2023届陕西省高三下学期4月考前冲刺训练(陕西适用)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2022·吕梁模拟)已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B等于( )
A.(-1,4) B.(-1,3)
C.(0,3) D.(0,4)
2.(2022·长春模拟)已知复数z的共轭复数=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.某校对240名职工线上教学期间的办公情况进行了调查统计,结果如图所示,下列表述错误的是( )
A.x=5.0
B.从该校任选一名职工,该职工不在家办公的概率为0.525
C.240名职工中有不到10名职工休假
D.该校在家办公或在校办公的职工不超过200名
4.(2022·芜湖模拟)设a=,b=ln π,c=lg ,则a,b,c的大小关系为( )
A.b>a>c B.c>a>b
C.a>b>c D.b>c>a
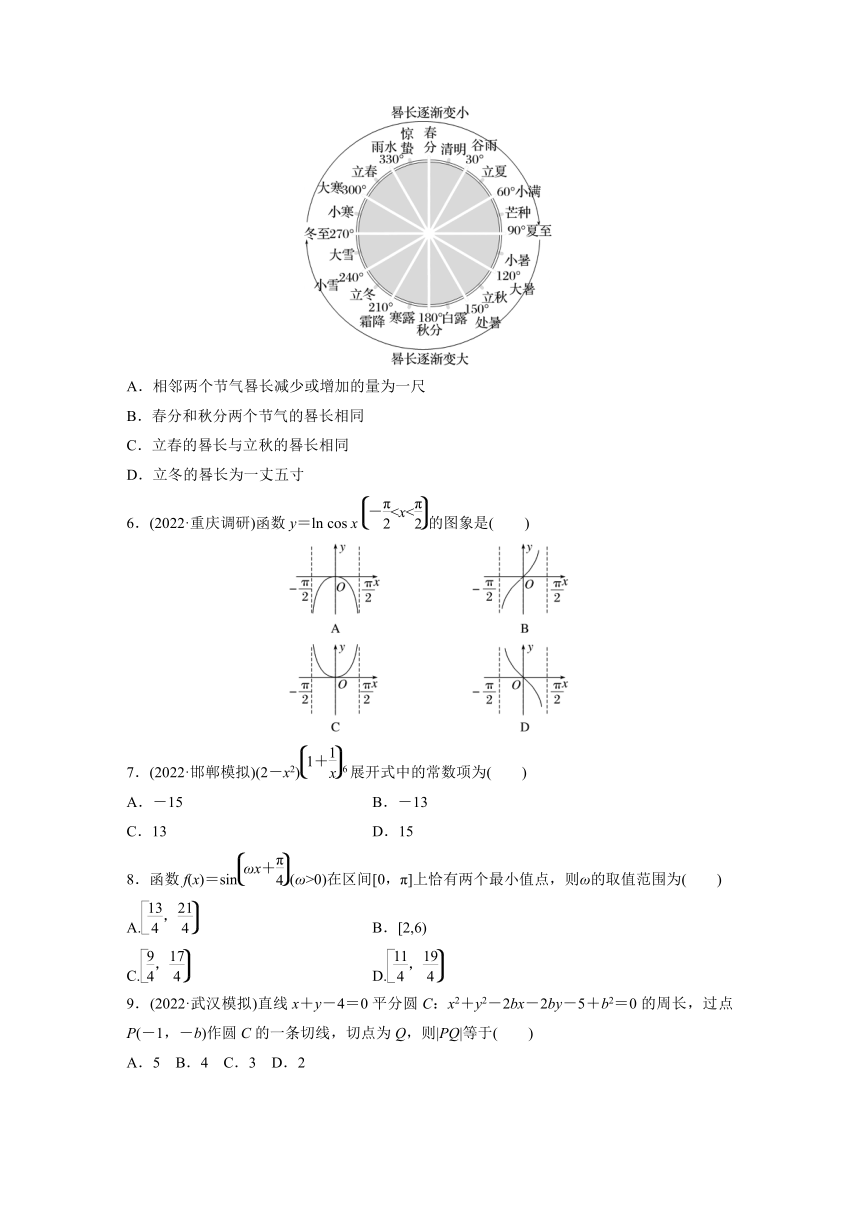
5.(2022·合肥模拟)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立春的晷长与立秋的晷长相同
D.立冬的晷长为一丈五寸
6.(2022·重庆调研)函数y=ln cos x的图象是( )
7.(2022·邯郸模拟)(2-x2)6展开式中的常数项为( )
A.-15 B.-13
C.13 D.15
8.函数f(x)=sin(ω>0)在区间[0,π]上恰有两个最小值点,则ω的取值范围为( )
A. B.[2,6)
C. D.
9.(2022·武汉模拟)直线x+y-4=0平分圆C:x2+y2-2bx-2by-5+b2=0的周长,过点P(-1,-b)作圆C的一条切线,切点为Q,则|PQ|等于( )
A.5 B.4 C.3 D.2
10.(2022·郑州模拟)如图,在五面体ABCDEF中,四边形ABCD是正方形,AB=4,EF=2,△BCF,△ADE都是等边三角形,则五面体ABCDEF的体积为( )
A. B.
C. D.4
11.(2022·荆州模拟)甲、乙两人各有一个袋子,且每人袋中均装有除颜色外其他完全相同的2个红球和2个白球,每人从各自袋中随机取出一个球,若2个球同色,则甲胜,且将取出的2个球全部放入甲的袋子中;若2个球异色,则乙胜,且将取出的2个球全部放入乙的袋子中.则两次取球后,甲的袋子中恰有6个球的概率是( )
A. B. C. D.
12.(2022·成都模拟)已知双曲线x2-y2=a2(a>0)的左、右焦点分别为F1,F2,过点F2作斜率为的直线交双曲线的右支于A,B两点,则△AF1B的内切圆半径为( )
A. B. C.a D.a
二、填空题(本大题共4小题,每小题5分,共20分)
13.(2022·淮安模拟)已知平面向量a,b满足a=(1,2),|b|=,a·b=,则cos〈a,b〉=________.
14.(2022·淮南模拟)已知实数x,y满足条件若目标函数z=x+2y的最大值为6,则实数a=________.
15.(2022·朔州模拟)在△ABC中,角A,B,C所对的边分别为a,b,c,若A=,△ABC的面积S=(a+3),则a的最小值为________.
16.(2022·哈尔滨模拟)已知m>0,若对任意的x∈[1,+∞),不等式2mx-1-log4x≥0恒成立,则m的最小值为________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答)
(一)必考题:共60分.
17.(12分)(2022·秦皇岛模拟)已知递增的等差数列{an}满足a2+a4+a6+a8=36,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)设bn=,数列{bn}的前n项和为Sn,求Sn.
18.(12分)(2022·兰州模拟)重楼,中药名,具有清热解毒、消肿止痛、凉肝定惊之功效,具有极高的药用价值.近年来,随着重楼的药用潜力被不断开发,野生重楼资源已经满足不了市场的需求,巨大的经济价值提升了家种重楼的热度,某机构统计了近几年某地家种重楼年产量y(单位:吨),统计数据如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码x 1 2 3 4 5 6 7
年产量y/吨 130 180 320 390 460 550 630
(1)根据表中的统计数据,求出y关于x的线性回归方程;
(2)根据(1)中所求方程预测2024年该地家种重楼的年产量.
附:线性回归方程=x+中斜率和截距的最小二乘估计公式分别为
==,
=-.
19.(12分)(2022·新余模拟)如图,在三棱锥P-ABC中,已知PA=PB=PC=AB=AC,E是PA的中点.
(1)求证:平面PAB⊥平面BCE;
(2)若BC=AB,求二面角E-AB-C的正弦值.
20.(12分)(2022·长沙模拟)已知离心率为的椭圆C1:+=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上的一点,△PF1F2的周长为6,且F1为抛物线C2:y2=-2px(p>0)的焦点.
(1)求椭圆C1与抛物线C2的方程;
(2)过椭圆C1的左顶点Q的直线l交抛物线C2于A,B两点,点O为原点,射线OA,OB分别交椭圆于C,D两点,△OCD的面积为S1,△OAB的面积为S2.则是否存在直线l使得S2=S1?若存在,求出直线l的方程;若不存在,请说明理由.
21.(12分)(2022·潍坊模拟)已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调区间;
(2)当a=1时,令g(x)=.
①证明:当x>0时,g(x)>1;
②若数列{xn}(n∈N*)满足x1=,=g(xn),证明:2n(-1)<1.
(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做.则按所做的第一题计分)
[选修4—4:坐标系与参数方程]
22.(2022·洛阳模拟)在直角坐标系中,曲线C的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)射线θ=α与曲线C分别交于点A,B,求+的值.
[选修4—5:不等式选讲]
23.已知函数f(x)=|ax+2|+|2x-a|(a∈R).
(1)当a=1时,求不等式f(x)<6的解集;
(2)当-1≤a≤3时,求f(a-1)的最大值与最小值.
参考答案
1.C 2.D 3.C 4.A 5.C 6.A
7.B [依题意知6展开式的常数项是T1=1,含x-2的项为T3=C2=15x-2,
所以(2-x2)6展开式中的常数项为2×1+(-1)×15=-13.]
8.A [令t=ωx+,
因为x∈[0,π],
所以t∈,
则函数f(t)=sin t在t∈内恰有两个最小值点,
所以有≤ωπ+<,
因为ω>0,
所以≤ω<.]
9.B [圆C:x2+y2-2bx-2by-5+b2=0的圆心为C(b,b),
半径为r=.
因为直线x+y-4=0平分圆C:x2+y2-2bx-2by-5+b2=0的周长,
所以直线x+y-4=0经过C(b,b),所以b+b-4=0,故b=2,
所以r=3,P(-1,-2),C(2,2),
|PC|==5,
所以|PQ|==4.]
10.B [如图,过点F作FH⊥AB于点H,FS⊥CD于点S,过点E作EG⊥AB于点G,EQ⊥CD于点Q,连接HS,GQ,
则V五面体ABCDEF=2V四棱锥F-BCSH+V三棱柱HSF-GQE.
根据五面体的结构特征,将五面体的体积转化为两个相同的四棱锥和一个三棱柱的体积之和.
过点F作FM⊥HS于点M,
则易知FM⊥平面ABCD,FM2=FH2-HM2=FB2-HB2-HM2
=11,
所以FM=,
所以V四棱锥F-BCSH=×4×=,
V三棱柱HSF-GQE=×4××2=4,
故V五面体ABCDEF=+4=.]
11.A [由题知,若两次取球后,甲的袋子中恰有6个球,则两次取球均为甲胜,即两次取球均为同色.
若第一次取球甲、乙都取到红球,概率为×=,则第一次取球后甲的袋子中有3个红球和2个白球,乙的袋子中有1个红球和2个白球;第二次取同色球分为取到红球或取到白球,概率为×+×=,故第一次取球甲﹑乙都取到红球且两次取球后,甲的袋子中有6个球的概率为.同理,第一次取球甲、乙都取到白球且两次取球后,甲的袋子中有6个球的概率为.
故所求概率为+=.]
12.C [如图,
不妨设A在第一象限,A(x1,y1),过点A作AM⊥x轴于点M,
得F2(a,0),
则|AF2|2=(x1-a)2+y
=(x1-a)2+x-a2
=2x-2ax1+a2=(x1-a)2,
所以|AF2|=x1-a.(*)
又∠AF2M=60°,
则|AF2|cos 60°=|F2M|
=x1-a,
即x1=|AF2|+a,
代入(*)式得
|AF2|=-a,
即|AF2|=(2+)a,
同理|BF2|=(2-)a,
则|AB|=4a,
=|F1F2|·|AB|sin 60°=2a2,
故△AF1B的内切圆半径r满足
(|F1A|+|F1B|+|AB|)r=,
又|F1A|+|F1B|=|AB|+4a=8a,
所以×12a×r=2a2,
解得r=a.]
13. 14.4
15.6
解析 在△ABC中,由A=及余弦定理得
a2=b2+c2-2bccos =b2+c2-bc≥2bc-bc=bc.
即bc≤a2,当且仅当b=c时取等号.
又S=bcsin A=bc=(a+3),
所以bc=4a+12,a2≥bc=4a+12,
即a2-4a-12≥0,
解得a≥6(a≤-2舍去),
所以a的最小值为6.
16.
解析 2mx-1-log4x≥0变形为2mx-1-log2x≥0,
即2mx≥log2x,
mx·2mx≥log2x·,
设f(t)=t·2t(t>0),
f′(t)=2t+t·2tln 2>0,
则f(t)是增函数,
由f(mx)≥f(log2x)恒成立得
mx≥log2x,即m≥,
设g(x)=(x≥1),
g′(x)=,
当10,g(x)单调递增,
当x>e时,g′(x)<0,g(x)单调递减,
所以g(x)max=g(e)=,
所以m≥,
即m的最小值是.
17.解 (1)设等差数列{an}的公差为d,
由题可知d>0,
因为a2+a4+a6+a8=4a5=36,
所以a5=9,
又a8是a5与a13的等比中项,
所以a=a5a13,
即(a5+3d)2=a5(a5+8d),
解得d=2或d=0(舍去),
所以an=a5+(n-5)d=2n-1.
(2)因为bn=,
所以bn=
=.
Sn=b1+b2+b3+…+bn
=
==.
18.解 (1)由表格数据,
得==4,
==380,
iyi=1×130+2×180+3×320+4×390+5×460+6×550+7×630=13 020,
=1+4+9+16+25+36+49=140,
则===85,
所以=-=380-85×4=40,
所以y关于x的线性回归方程为
=85x+40.
(2)由题可知,2024年的年份代码为9,即x=9,
将x=9代入线性回归方程,
得=85×9+40=805,
所以预测2024年该地家种重楼的年产量为805吨.
19.(1)证明 因为PB=AB,E是PA的中点,
所以PA⊥BE,
同理可得PA⊥CE,
因为BE∩CE=E,BE,CE 平面BCE,
所以PA⊥平面BCE.
因为PA 平面PAB,
所以平面PAB⊥平面BCE.
(2)解 设AB=2,
因为BC=AB,
所以BC=,
又BE=CE=,
所以BE2+CE2=BC2,
所以BE⊥CE.
如图,以点E为坐标原点,EB,EC,EP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系E-xyz,
则E(0,0,0),A(0,0,-1),B(,0,0),C(0,,0),
所以=(,0,1),=(0,,1),
设平面ABC的法向量为n1=(x,y,z),
则即
令x=,可得z=-3,y=,
所以平面ABC的一个法向量为n1=(,,-3).
易知CE⊥平面ABE,所以平面ABE的一个法向量为n2=(0,1,0),
所以cos〈n1,n2〉=
==,
所以二面角E-AB-C的正弦值为.
20.解 (1)由题意得
解得
∴椭圆C1的方程为+=1,
F1(-1,0),
∴抛物线C2的方程为y2=-4x.
(2)由题意得,直线l的斜率不为0,
Q(-2,0),
设直线l的方程为x=my-2,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由得y2+4my-8=0,
∴y1+y2=-4m,y1y2=-8,
∵S2=S1,
∴=
==
==,
∵y=-4x1,
∴直线OA的斜率为=-,
即直线OA的方程为y=-x,
由得y=,
同理可得y=,
y·y=×
=
=
=,
∴2=
==,
解得m=±1,
∴存在直线l,方程为x-y+2=0或x+y+2=0.
21.(1)解 函数f(x)=ex-ax-a的定义域为R,f′(x)=ex-a,
当a≤0时,f′(x)>0恒成立,
即f(x)在(-∞,+∞)上单调递增,
当a>0时,令f′(x)=ex-a>0,
解得x>ln a,
令f′(x)=ex-a<0,解得x即f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增,
所以当a≤0时,f(x)的单调递增区间为(-∞,+∞),
当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞).
(2)证明 当a=1时,g(x)=,
①当x>0时,>1 ex>1+x+ <1,
令F(x)=-1,x>0,
则F′(x)=<0恒成立,
所以F(x)在(0,+∞)上单调递减,
F(x)因此<1成立,
所以当x>0时,g(x)>1.
②由①可知,当x∈(0,+∞)时,g(x)>1,
由x1=得=g(x1)>1,即x2>0,
由=g(xn),可得xn>0,
而-1=-1,
又e-3=e-<0,
即<,
则-1=-1<,
由于2n(-1)<1 -1只需证-1<(-1) g(xn)-1<-,
又当x>0时,g(x)-10 +1>0,
令h(x)=+1,x>0,
h′(x)=>0恒成立,
则h(x)在(0,+∞)上单调递增,
h(x)>h(0)=0,
则当x>0时,恒有+1>0,而xn>0,
即g(xn)-1<-成立,不等式-1<(-1)成立,
因此-1<(-1)<(-1)<…<(-1)<成立,
即-1所以原不等式得证.
22.解 (1)因为
所以(x+2)2+(y-1)2=1,
即x2+y2+4x-2y+4=0,
所以曲线C的极坐标方程为
ρ2+4ρcos θ-2ρsin θ+4=0.
(2)依题意知
<α<π且tan α=-,
所以
解得sin α=,cos α=-.
将(ρ,α)代入ρ2+4ρcos θ-2ρsin θ+4=0得ρ2-ρ+4=0,
Δ=2-16>0.
设|OA|=ρ1,|OB|=ρ2,
则ρ1+ρ2=,ρ1·ρ2=4,
所以+=+
==.
23.解 (1)当a=1时,不等式f(x)<6 |x+2|+|2x-1|<6,则
由解得-由解得-2≤x≤,
由解得综上,-所以不等式f(x)<6的解集为.
(2)依题意,f(a-1)=|a2-a+2|+|a-2|=a2-a+2+|a-2|,
当-1≤a<2时,f(a-1)=a2-a+2-a+2=a2-2a+4=(a-1)2+3,
当a=1时,f(a-1)取得最小值3,
当a=-1时,f(a-1)取得最大值7,
因此f(a-1)∈[3,7];
当2≤a≤3时,
f(a-1)=a2-a+2+a-2=a2,
此时f(a-1)在a∈[2,3]上单调递增,
当a=2时,a2=4,
当a=3时,a2=9,因此f(a-1)∈[4,9],
综上,f(a-1)的最大值为9,最小值为3.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2022·吕梁模拟)已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B等于( )
A.(-1,4) B.(-1,3)
C.(0,3) D.(0,4)
2.(2022·长春模拟)已知复数z的共轭复数=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.某校对240名职工线上教学期间的办公情况进行了调查统计,结果如图所示,下列表述错误的是( )
A.x=5.0
B.从该校任选一名职工,该职工不在家办公的概率为0.525
C.240名职工中有不到10名职工休假
D.该校在家办公或在校办公的职工不超过200名
4.(2022·芜湖模拟)设a=,b=ln π,c=lg ,则a,b,c的大小关系为( )
A.b>a>c B.c>a>b
C.a>b>c D.b>c>a
5.(2022·合肥模拟)我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立春的晷长与立秋的晷长相同
D.立冬的晷长为一丈五寸
6.(2022·重庆调研)函数y=ln cos x的图象是( )
7.(2022·邯郸模拟)(2-x2)6展开式中的常数项为( )
A.-15 B.-13
C.13 D.15
8.函数f(x)=sin(ω>0)在区间[0,π]上恰有两个最小值点,则ω的取值范围为( )
A. B.[2,6)
C. D.
9.(2022·武汉模拟)直线x+y-4=0平分圆C:x2+y2-2bx-2by-5+b2=0的周长,过点P(-1,-b)作圆C的一条切线,切点为Q,则|PQ|等于( )
A.5 B.4 C.3 D.2
10.(2022·郑州模拟)如图,在五面体ABCDEF中,四边形ABCD是正方形,AB=4,EF=2,△BCF,△ADE都是等边三角形,则五面体ABCDEF的体积为( )
A. B.
C. D.4
11.(2022·荆州模拟)甲、乙两人各有一个袋子,且每人袋中均装有除颜色外其他完全相同的2个红球和2个白球,每人从各自袋中随机取出一个球,若2个球同色,则甲胜,且将取出的2个球全部放入甲的袋子中;若2个球异色,则乙胜,且将取出的2个球全部放入乙的袋子中.则两次取球后,甲的袋子中恰有6个球的概率是( )
A. B. C. D.
12.(2022·成都模拟)已知双曲线x2-y2=a2(a>0)的左、右焦点分别为F1,F2,过点F2作斜率为的直线交双曲线的右支于A,B两点,则△AF1B的内切圆半径为( )
A. B. C.a D.a
二、填空题(本大题共4小题,每小题5分,共20分)
13.(2022·淮安模拟)已知平面向量a,b满足a=(1,2),|b|=,a·b=,则cos〈a,b〉=________.
14.(2022·淮南模拟)已知实数x,y满足条件若目标函数z=x+2y的最大值为6,则实数a=________.
15.(2022·朔州模拟)在△ABC中,角A,B,C所对的边分别为a,b,c,若A=,△ABC的面积S=(a+3),则a的最小值为________.
16.(2022·哈尔滨模拟)已知m>0,若对任意的x∈[1,+∞),不等式2mx-1-log4x≥0恒成立,则m的最小值为________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答)
(一)必考题:共60分.
17.(12分)(2022·秦皇岛模拟)已知递增的等差数列{an}满足a2+a4+a6+a8=36,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)设bn=,数列{bn}的前n项和为Sn,求Sn.
18.(12分)(2022·兰州模拟)重楼,中药名,具有清热解毒、消肿止痛、凉肝定惊之功效,具有极高的药用价值.近年来,随着重楼的药用潜力被不断开发,野生重楼资源已经满足不了市场的需求,巨大的经济价值提升了家种重楼的热度,某机构统计了近几年某地家种重楼年产量y(单位:吨),统计数据如表所示.
年份 2016 2017 2018 2019 2020 2021 2022
年份代码x 1 2 3 4 5 6 7
年产量y/吨 130 180 320 390 460 550 630
(1)根据表中的统计数据,求出y关于x的线性回归方程;
(2)根据(1)中所求方程预测2024年该地家种重楼的年产量.
附:线性回归方程=x+中斜率和截距的最小二乘估计公式分别为
==,
=-.
19.(12分)(2022·新余模拟)如图,在三棱锥P-ABC中,已知PA=PB=PC=AB=AC,E是PA的中点.
(1)求证:平面PAB⊥平面BCE;
(2)若BC=AB,求二面角E-AB-C的正弦值.
20.(12分)(2022·长沙模拟)已知离心率为的椭圆C1:+=1(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上的一点,△PF1F2的周长为6,且F1为抛物线C2:y2=-2px(p>0)的焦点.
(1)求椭圆C1与抛物线C2的方程;
(2)过椭圆C1的左顶点Q的直线l交抛物线C2于A,B两点,点O为原点,射线OA,OB分别交椭圆于C,D两点,△OCD的面积为S1,△OAB的面积为S2.则是否存在直线l使得S2=S1?若存在,求出直线l的方程;若不存在,请说明理由.
21.(12分)(2022·潍坊模拟)已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调区间;
(2)当a=1时,令g(x)=.
①证明:当x>0时,g(x)>1;
②若数列{xn}(n∈N*)满足x1=,=g(xn),证明:2n(-1)<1.
(二)选考题(共10分.请考生在第22、23题中任选一题作答.如果多做.则按所做的第一题计分)
[选修4—4:坐标系与参数方程]
22.(2022·洛阳模拟)在直角坐标系中,曲线C的参数方程是(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)射线θ=α与曲线C分别交于点A,B,求+的值.
[选修4—5:不等式选讲]
23.已知函数f(x)=|ax+2|+|2x-a|(a∈R).
(1)当a=1时,求不等式f(x)<6的解集;
(2)当-1≤a≤3时,求f(a-1)的最大值与最小值.
参考答案
1.C 2.D 3.C 4.A 5.C 6.A
7.B [依题意知6展开式的常数项是T1=1,含x-2的项为T3=C2=15x-2,
所以(2-x2)6展开式中的常数项为2×1+(-1)×15=-13.]
8.A [令t=ωx+,
因为x∈[0,π],
所以t∈,
则函数f(t)=sin t在t∈内恰有两个最小值点,
所以有≤ωπ+<,
因为ω>0,
所以≤ω<.]
9.B [圆C:x2+y2-2bx-2by-5+b2=0的圆心为C(b,b),
半径为r=.
因为直线x+y-4=0平分圆C:x2+y2-2bx-2by-5+b2=0的周长,
所以直线x+y-4=0经过C(b,b),所以b+b-4=0,故b=2,
所以r=3,P(-1,-2),C(2,2),
|PC|==5,
所以|PQ|==4.]
10.B [如图,过点F作FH⊥AB于点H,FS⊥CD于点S,过点E作EG⊥AB于点G,EQ⊥CD于点Q,连接HS,GQ,
则V五面体ABCDEF=2V四棱锥F-BCSH+V三棱柱HSF-GQE.
根据五面体的结构特征,将五面体的体积转化为两个相同的四棱锥和一个三棱柱的体积之和.
过点F作FM⊥HS于点M,
则易知FM⊥平面ABCD,FM2=FH2-HM2=FB2-HB2-HM2
=11,
所以FM=,
所以V四棱锥F-BCSH=×4×=,
V三棱柱HSF-GQE=×4××2=4,
故V五面体ABCDEF=+4=.]
11.A [由题知,若两次取球后,甲的袋子中恰有6个球,则两次取球均为甲胜,即两次取球均为同色.
若第一次取球甲、乙都取到红球,概率为×=,则第一次取球后甲的袋子中有3个红球和2个白球,乙的袋子中有1个红球和2个白球;第二次取同色球分为取到红球或取到白球,概率为×+×=,故第一次取球甲﹑乙都取到红球且两次取球后,甲的袋子中有6个球的概率为.同理,第一次取球甲、乙都取到白球且两次取球后,甲的袋子中有6个球的概率为.
故所求概率为+=.]
12.C [如图,
不妨设A在第一象限,A(x1,y1),过点A作AM⊥x轴于点M,
得F2(a,0),
则|AF2|2=(x1-a)2+y
=(x1-a)2+x-a2
=2x-2ax1+a2=(x1-a)2,
所以|AF2|=x1-a.(*)
又∠AF2M=60°,
则|AF2|cos 60°=|F2M|
=x1-a,
即x1=|AF2|+a,
代入(*)式得
|AF2|=-a,
即|AF2|=(2+)a,
同理|BF2|=(2-)a,
则|AB|=4a,
=|F1F2|·|AB|sin 60°=2a2,
故△AF1B的内切圆半径r满足
(|F1A|+|F1B|+|AB|)r=,
又|F1A|+|F1B|=|AB|+4a=8a,
所以×12a×r=2a2,
解得r=a.]
13. 14.4
15.6
解析 在△ABC中,由A=及余弦定理得
a2=b2+c2-2bccos =b2+c2-bc≥2bc-bc=bc.
即bc≤a2,当且仅当b=c时取等号.
又S=bcsin A=bc=(a+3),
所以bc=4a+12,a2≥bc=4a+12,
即a2-4a-12≥0,
解得a≥6(a≤-2舍去),
所以a的最小值为6.
16.
解析 2mx-1-log4x≥0变形为2mx-1-log2x≥0,
即2mx≥log2x,
mx·2mx≥log2x·,
设f(t)=t·2t(t>0),
f′(t)=2t+t·2tln 2>0,
则f(t)是增函数,
由f(mx)≥f(log2x)恒成立得
mx≥log2x,即m≥,
设g(x)=(x≥1),
g′(x)=,
当1
当x>e时,g′(x)<0,g(x)单调递减,
所以g(x)max=g(e)=,
所以m≥,
即m的最小值是.
17.解 (1)设等差数列{an}的公差为d,
由题可知d>0,
因为a2+a4+a6+a8=4a5=36,
所以a5=9,
又a8是a5与a13的等比中项,
所以a=a5a13,
即(a5+3d)2=a5(a5+8d),
解得d=2或d=0(舍去),
所以an=a5+(n-5)d=2n-1.
(2)因为bn=,
所以bn=
=.
Sn=b1+b2+b3+…+bn
=
==.
18.解 (1)由表格数据,
得==4,
==380,
iyi=1×130+2×180+3×320+4×390+5×460+6×550+7×630=13 020,
=1+4+9+16+25+36+49=140,
则===85,
所以=-=380-85×4=40,
所以y关于x的线性回归方程为
=85x+40.
(2)由题可知,2024年的年份代码为9,即x=9,
将x=9代入线性回归方程,
得=85×9+40=805,
所以预测2024年该地家种重楼的年产量为805吨.
19.(1)证明 因为PB=AB,E是PA的中点,
所以PA⊥BE,
同理可得PA⊥CE,
因为BE∩CE=E,BE,CE 平面BCE,
所以PA⊥平面BCE.
因为PA 平面PAB,
所以平面PAB⊥平面BCE.
(2)解 设AB=2,
因为BC=AB,
所以BC=,
又BE=CE=,
所以BE2+CE2=BC2,
所以BE⊥CE.
如图,以点E为坐标原点,EB,EC,EP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系E-xyz,
则E(0,0,0),A(0,0,-1),B(,0,0),C(0,,0),
所以=(,0,1),=(0,,1),
设平面ABC的法向量为n1=(x,y,z),
则即
令x=,可得z=-3,y=,
所以平面ABC的一个法向量为n1=(,,-3).
易知CE⊥平面ABE,所以平面ABE的一个法向量为n2=(0,1,0),
所以cos〈n1,n2〉=
==,
所以二面角E-AB-C的正弦值为.
20.解 (1)由题意得
解得
∴椭圆C1的方程为+=1,
F1(-1,0),
∴抛物线C2的方程为y2=-4x.
(2)由题意得,直线l的斜率不为0,
Q(-2,0),
设直线l的方程为x=my-2,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由得y2+4my-8=0,
∴y1+y2=-4m,y1y2=-8,
∵S2=S1,
∴=
==
==,
∵y=-4x1,
∴直线OA的斜率为=-,
即直线OA的方程为y=-x,
由得y=,
同理可得y=,
y·y=×
=
=
=,
∴2=
==,
解得m=±1,
∴存在直线l,方程为x-y+2=0或x+y+2=0.
21.(1)解 函数f(x)=ex-ax-a的定义域为R,f′(x)=ex-a,
当a≤0时,f′(x)>0恒成立,
即f(x)在(-∞,+∞)上单调递增,
当a>0时,令f′(x)=ex-a>0,
解得x>ln a,
令f′(x)=ex-a<0,解得x
所以当a≤0时,f(x)的单调递增区间为(-∞,+∞),
当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞).
(2)证明 当a=1时,g(x)=,
①当x>0时,>1 ex>1+x+ <1,
令F(x)=-1,x>0,
则F′(x)=<0恒成立,
所以F(x)在(0,+∞)上单调递减,
F(x)
所以当x>0时,g(x)>1.
②由①可知,当x∈(0,+∞)时,g(x)>1,
由x1=得=g(x1)>1,即x2>0,
由=g(xn),可得xn>0,
而-1=-1,
又e-3=e-<0,
即<,
则-1=-1<,
由于2n(-1)<1 -1
又当x>0时,g(x)-1
令h(x)=+1,x>0,
h′(x)=>0恒成立,
则h(x)在(0,+∞)上单调递增,
h(x)>h(0)=0,
则当x>0时,恒有+1>0,而xn>0,
即g(xn)-1<-成立,不等式-1<(-1)成立,
因此-1<(-1)<(-1)<…<(-1)<成立,
即-1
22.解 (1)因为
所以(x+2)2+(y-1)2=1,
即x2+y2+4x-2y+4=0,
所以曲线C的极坐标方程为
ρ2+4ρcos θ-2ρsin θ+4=0.
(2)依题意知
<α<π且tan α=-,
所以
解得sin α=,cos α=-.
将(ρ,α)代入ρ2+4ρcos θ-2ρsin θ+4=0得ρ2-ρ+4=0,
Δ=2-16>0.
设|OA|=ρ1,|OB|=ρ2,
则ρ1+ρ2=,ρ1·ρ2=4,
所以+=+
==.
23.解 (1)当a=1时,不等式f(x)<6 |x+2|+|2x-1|<6,则
由解得-
由解得
(2)依题意,f(a-1)=|a2-a+2|+|a-2|=a2-a+2+|a-2|,
当-1≤a<2时,f(a-1)=a2-a+2-a+2=a2-2a+4=(a-1)2+3,
当a=1时,f(a-1)取得最小值3,
当a=-1时,f(a-1)取得最大值7,
因此f(a-1)∈[3,7];
当2≤a≤3时,
f(a-1)=a2-a+2+a-2=a2,
此时f(a-1)在a∈[2,3]上单调递增,
当a=2时,a2=4,
当a=3时,a2=9,因此f(a-1)∈[4,9],
综上,f(a-1)的最大值为9,最小值为3.
同课章节目录
