8.1基本立体图形 课件(共19张PPT)
文档属性
| 名称 | 8.1基本立体图形 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-22 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
【活动1】动手折一折、捏一捏
在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体(space geometry).
感受新知
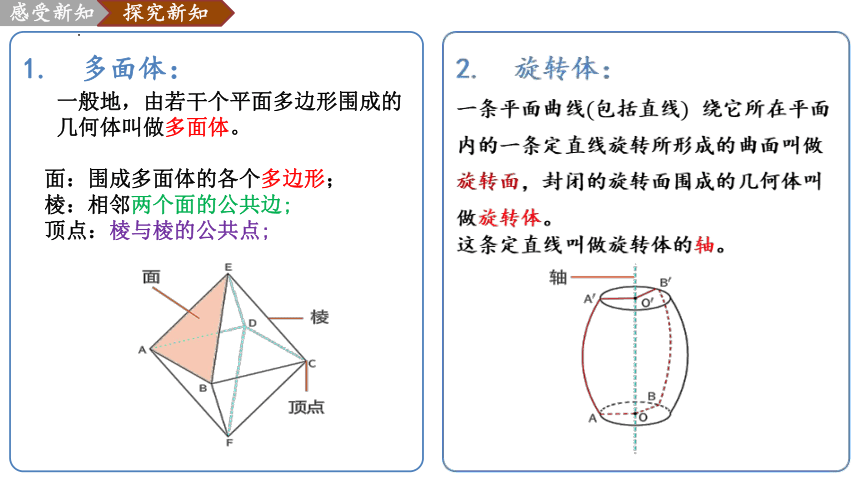
1. 多面体:
一般地,由若干个平面多边形围成的几何体叫做多面体。
面:围成多面体的各个多边形;
棱:相邻两个面的公共边;
顶点:棱与棱的公共点;
旋转体:
一条平面曲线包括直线 绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
感受新知
探究新知
8.1 基本立体图形
棱柱、棱锥、棱台
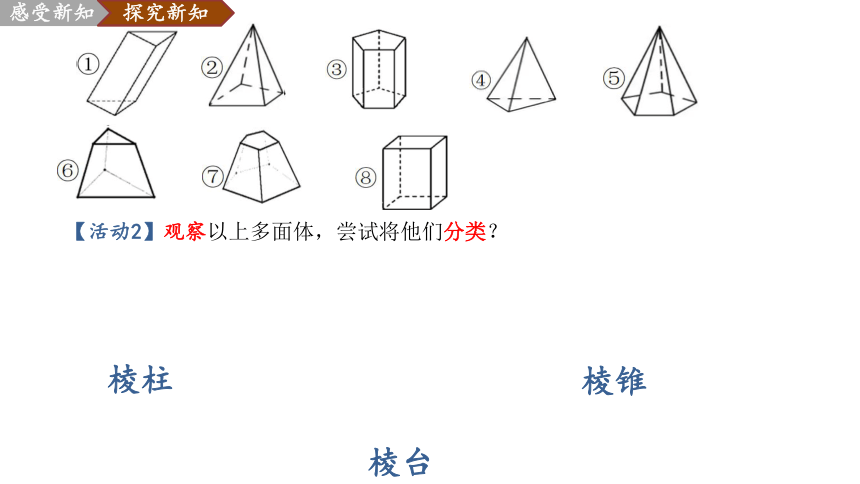
【活动2】观察以上多面体,尝试将他们分类?
棱柱
棱锥
棱台
感受新知
探究新知
【活动3】自学课本P98-P99:1.棱柱
活动要求:1.默读文字,并用红笔勾画关键词
2.在导学案上填空:棱柱的定义、相关概念、
棱柱如何表示、如何分类
感受新知
探究新知
棱柱的定义:
一般地,有______________,其余各面都是_______,并且相邻两个四边形的公共边都________,由这些面所围成的几何体叫做棱柱。
棱柱
【自学反馈】完成填空
两个面互相平行
四边形
互相平行
感受新知
探究新知
感受新知
探究新知
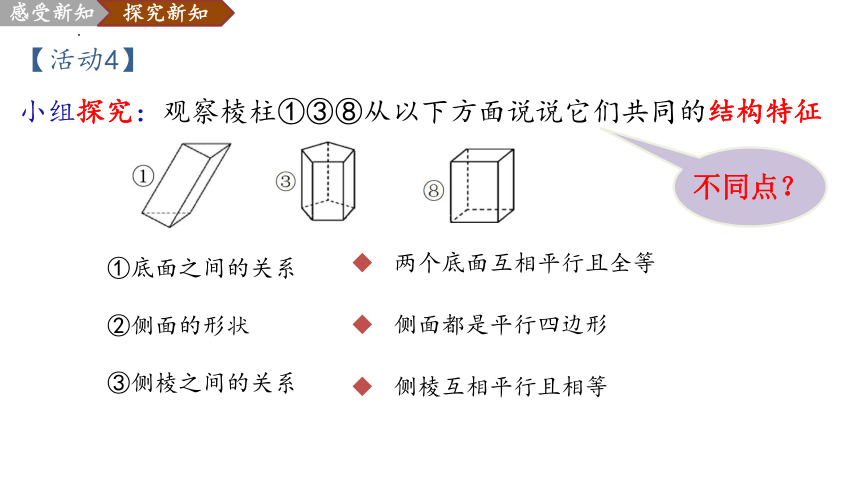
【活动4】
小组探究:观察棱柱①③⑧从以下方面说说它们共同的结构特征
①底面之间的关系
②侧面的形状
③侧棱之间的关系
侧棱互相平行且相等
侧面都是平行四边形
两个底面互相平行且全等
不同点?
【活动5】思考:观察棱柱①③⑧,你觉得可以怎么分类?
感受新知
探究新知
按底面多边形的边数分:
特殊棱柱:
三棱柱
五棱柱
四棱柱
斜棱柱
直棱柱
正棱柱
平行六面体
追问:正方体、长方体与平行六面体的关系?
如图,下列几何体中为棱柱的是____________________(填写序号)
感受新知
探究新知
应用新知
练习1:
(1)、(3)、(5)
感受新知
例1下列说法正确的是( )
应用新知
探究新知
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.五棱柱有5条侧棱,5个侧面,侧面均为平行四边形
D
【活动6】自学课本P99-P100:2.棱锥
活动要求: 1.默读文字,并用红笔勾画关键词
2.在导学案上填空:棱锥的定义、相关概念、
棱锥如何表示、如何分类
感受新知
探究新知
2、棱锥
2. 棱锥:
一般地,有一个面是_______,其余各面是有______________的_________, 由这些面所围成的几何体叫做棱锥
分类:
按底面多边形的边数分类______________________;
特殊的棱锥:______;
结构特征:
多边形
一个公共顶点
三角形
正棱锥
三棱锥(四面体)、四棱锥、...
感受新知
探究新知
侧面都是有一个公共顶点的三角形
各侧棱交于一点
底面是多边形
感受新知
探究新知
应用新知
辨析1:有一个面是多边形,其余各面都是三角形,这个多面体是棱锥么?
不一定
3. 棱台:
用一个_____________________________,我们把____________
之间的那部分多面体叫做棱台
分类:__________________;
特殊的棱台:_________;
结构特征
【类比探究】
感受新知
探究新知
平行于棱锥底面的平面去截棱锥
底面和截面
三棱台、四棱台、...
正棱台
上底面
下底面
侧面都是梯形
底面是平行且相似的多边形
各侧棱延长线交于一点
辨析2:下列几何体是不是棱台,为什么
(1)
(2)
感受新知
探究新知
应用新知
不是
例2.将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱棱锥,棱台,直棱柱,四面体,
平行六面体
感受新知
探究新知
应用新知
感受新知
探究新知
梳理总结
应用新知
感受新知
探究新知
梳理总结
应用新知
观察
观察
观察
类比
四棱柱和平行六面体
长方体与直四棱柱的关系
棱台侧棱的特征
棱锥的侧面有公共顶点
类比转化
分类讨论
回归定义
观察周围的物体
旋转体与多面体
棱柱棱锥棱台的定义及结构特征
它们的分类、各类间的关系
直观想象
感受新知
探究新知
作业布置
应用新知
梳理总结
1.课本105页习题8.1第1、2、6题
2.每个小组动手折一个棱柱、棱锥、棱台
作业:
【活动1】动手折一折、捏一捏
在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体(space geometry).
感受新知
1. 多面体:
一般地,由若干个平面多边形围成的几何体叫做多面体。
面:围成多面体的各个多边形;
棱:相邻两个面的公共边;
顶点:棱与棱的公共点;
旋转体:
一条平面曲线包括直线 绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体。
这条定直线叫做旋转体的轴。
感受新知
探究新知
8.1 基本立体图形
棱柱、棱锥、棱台
【活动2】观察以上多面体,尝试将他们分类?
棱柱
棱锥
棱台
感受新知
探究新知
【活动3】自学课本P98-P99:1.棱柱
活动要求:1.默读文字,并用红笔勾画关键词
2.在导学案上填空:棱柱的定义、相关概念、
棱柱如何表示、如何分类
感受新知
探究新知
棱柱的定义:
一般地,有______________,其余各面都是_______,并且相邻两个四边形的公共边都________,由这些面所围成的几何体叫做棱柱。
棱柱
【自学反馈】完成填空
两个面互相平行
四边形
互相平行
感受新知
探究新知
感受新知
探究新知
【活动4】
小组探究:观察棱柱①③⑧从以下方面说说它们共同的结构特征
①底面之间的关系
②侧面的形状
③侧棱之间的关系
侧棱互相平行且相等
侧面都是平行四边形
两个底面互相平行且全等
不同点?
【活动5】思考:观察棱柱①③⑧,你觉得可以怎么分类?
感受新知
探究新知
按底面多边形的边数分:
特殊棱柱:
三棱柱
五棱柱
四棱柱
斜棱柱
直棱柱
正棱柱
平行六面体
追问:正方体、长方体与平行六面体的关系?
如图,下列几何体中为棱柱的是____________________(填写序号)
感受新知
探究新知
应用新知
练习1:
(1)、(3)、(5)
感受新知
例1下列说法正确的是( )
应用新知
探究新知
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C.各侧面都是正方形的四棱柱一定是正方体
D.五棱柱有5条侧棱,5个侧面,侧面均为平行四边形
D
【活动6】自学课本P99-P100:2.棱锥
活动要求: 1.默读文字,并用红笔勾画关键词
2.在导学案上填空:棱锥的定义、相关概念、
棱锥如何表示、如何分类
感受新知
探究新知
2、棱锥
2. 棱锥:
一般地,有一个面是_______,其余各面是有______________的_________, 由这些面所围成的几何体叫做棱锥
分类:
按底面多边形的边数分类______________________;
特殊的棱锥:______;
结构特征:
多边形
一个公共顶点
三角形
正棱锥
三棱锥(四面体)、四棱锥、...
感受新知
探究新知
侧面都是有一个公共顶点的三角形
各侧棱交于一点
底面是多边形
感受新知
探究新知
应用新知
辨析1:有一个面是多边形,其余各面都是三角形,这个多面体是棱锥么?
不一定
3. 棱台:
用一个_____________________________,我们把____________
之间的那部分多面体叫做棱台
分类:__________________;
特殊的棱台:_________;
结构特征
【类比探究】
感受新知
探究新知
平行于棱锥底面的平面去截棱锥
底面和截面
三棱台、四棱台、...
正棱台
上底面
下底面
侧面都是梯形
底面是平行且相似的多边形
各侧棱延长线交于一点
辨析2:下列几何体是不是棱台,为什么
(1)
(2)
感受新知
探究新知
应用新知
不是
例2.将下列各类几何体之间的关系用Venn图表示出来:
多面体,长方体,棱柱棱锥,棱台,直棱柱,四面体,
平行六面体
感受新知
探究新知
应用新知
感受新知
探究新知
梳理总结
应用新知
感受新知
探究新知
梳理总结
应用新知
观察
观察
观察
类比
四棱柱和平行六面体
长方体与直四棱柱的关系
棱台侧棱的特征
棱锥的侧面有公共顶点
类比转化
分类讨论
回归定义
观察周围的物体
旋转体与多面体
棱柱棱锥棱台的定义及结构特征
它们的分类、各类间的关系
直观想象
感受新知
探究新知
作业布置
应用新知
梳理总结
1.课本105页习题8.1第1、2、6题
2.每个小组动手折一个棱柱、棱锥、棱台
作业:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
