2022—2023学年人教版数学八年级下册18.1.1平行四边形的性质 课件 (共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册18.1.1平行四边形的性质 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 09:34:42 | ||
图片预览

文档简介
(共15张PPT)
平行四边形
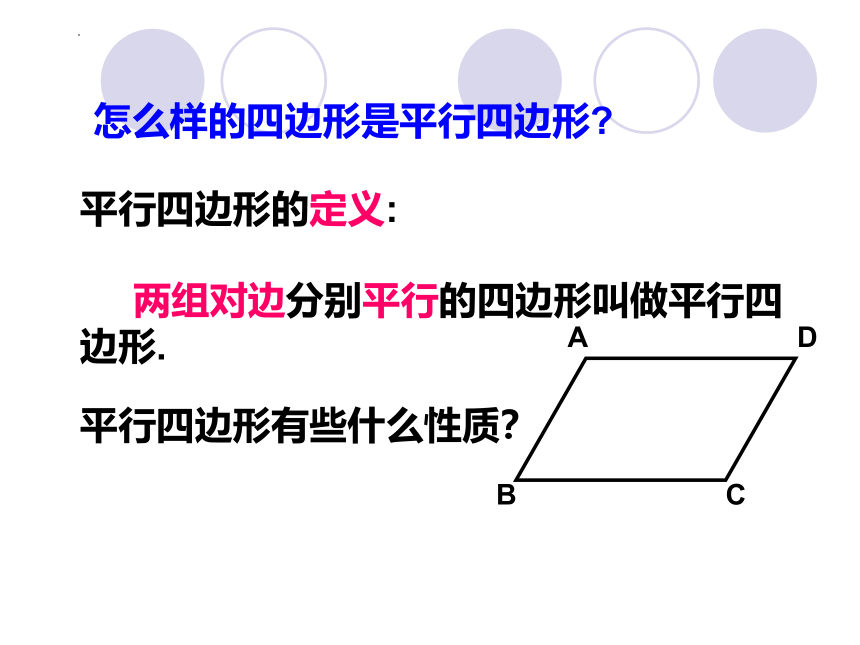
怎么样的四边形是平行四边形
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
平行四边形有些什么性质?
A
B
C
D
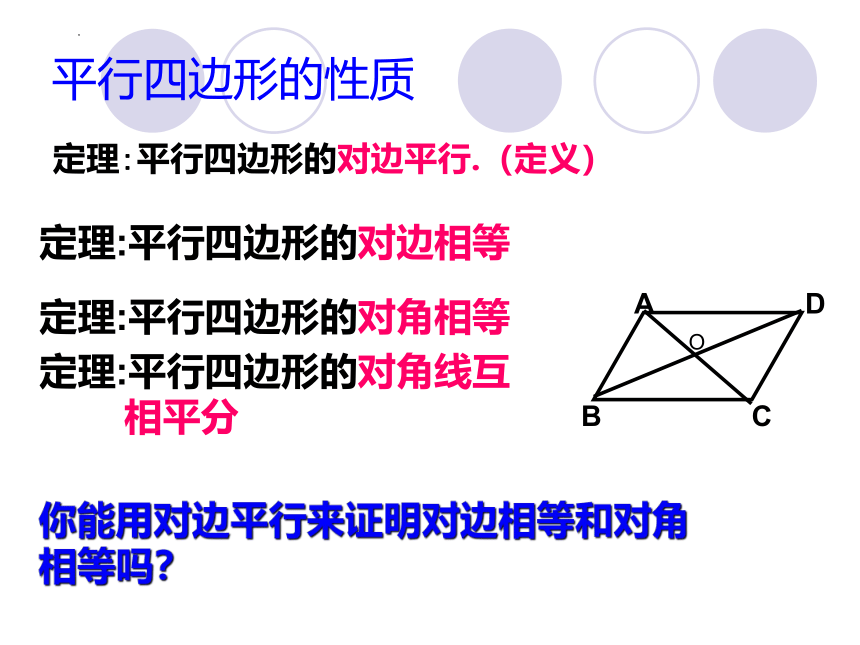
平行四边形的性质
定理:平行四边形的对边平行.(定义)
定理:平行四边形的对边相等
定理:平行四边形的对角相等
定理:平行四边形的对角线互
相平分
A
B
C
D
O
你能用对边平行来证明对边相等和对角相等吗?
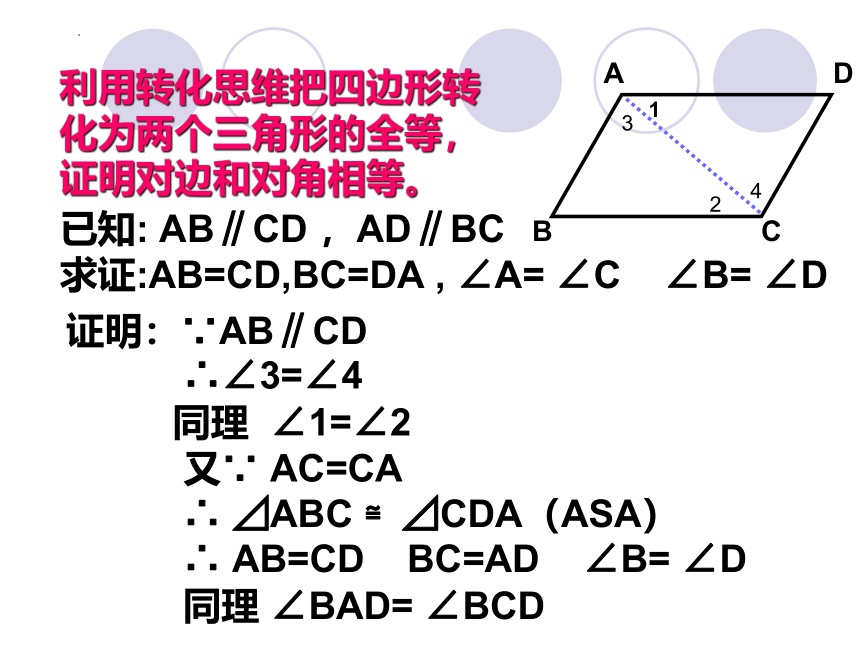
利用转化思维把四边形转 化为两个三角形的全等,证明对边和对角相等。
已知: AB∥CD ,AD∥BC
求证:AB=CD,BC=DA , ∠A= ∠C ∠B= ∠D
A
B
C
D
证明:∵AB∥CD
∴∠3=∠4
同理 ∠1=∠2
又∵ AC=CA
∴ ⊿ABC ≌⊿CDA(ASA)
∴ AB=CD BC=AD ∠B= ∠D
同理 ∠BAD= ∠BCD
1
2
3
4
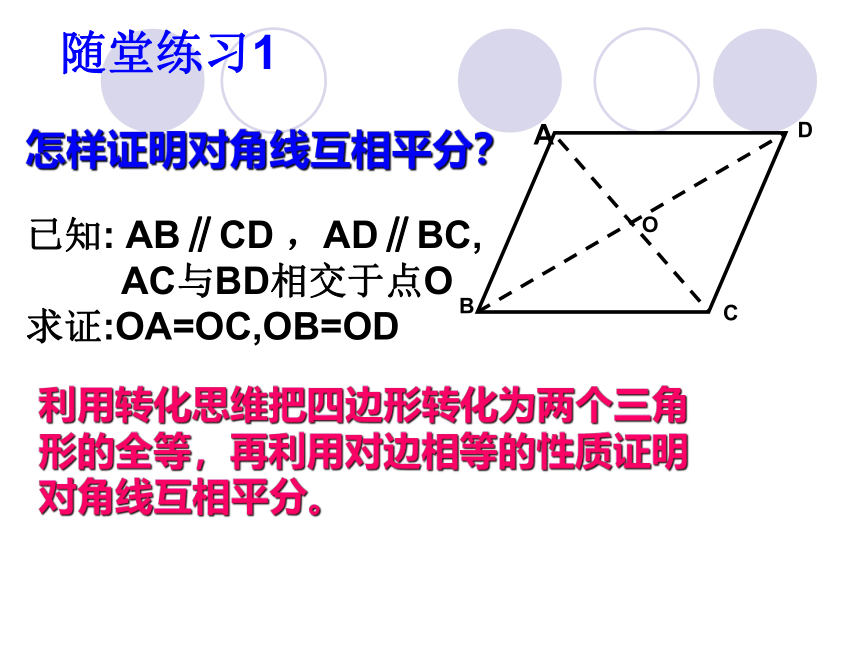
怎样证明对角线互相平分?
A
B
C
D
O
利用转化思维把四边形转化为两个三角形的全等,再利用对边相等的性质证明对角线互相平分。
随堂练习1
已知: AB∥CD ,AD∥BC,
AC与BD相交于点O
求证:OA=OC,OB=OD
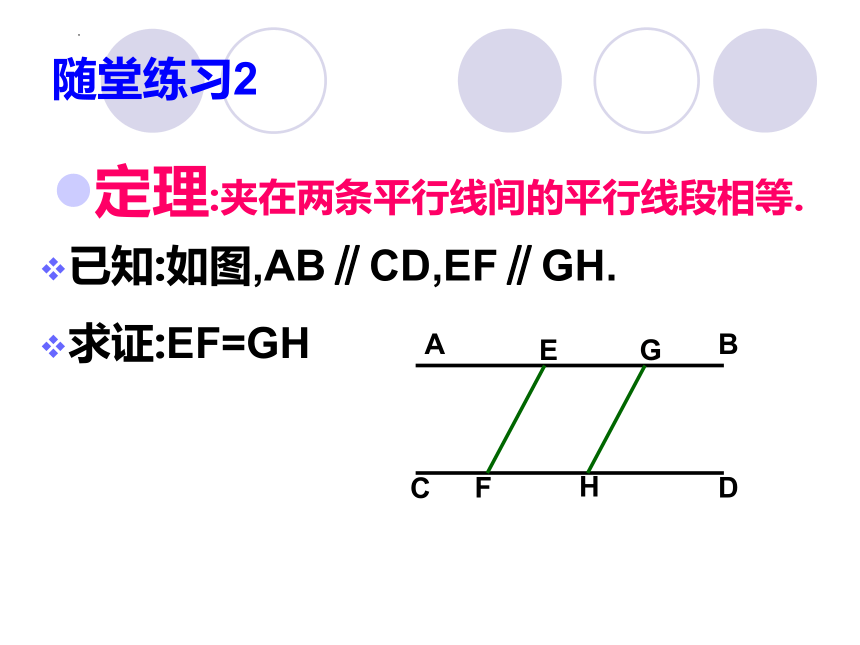
随堂练习2
定理:夹在两条平行线间的平行线段相等.
E
F
H
G
A
B
D
C
已知:如图,AB∥CD,EF∥GH.
求证:EF=GH
A
B
C
D
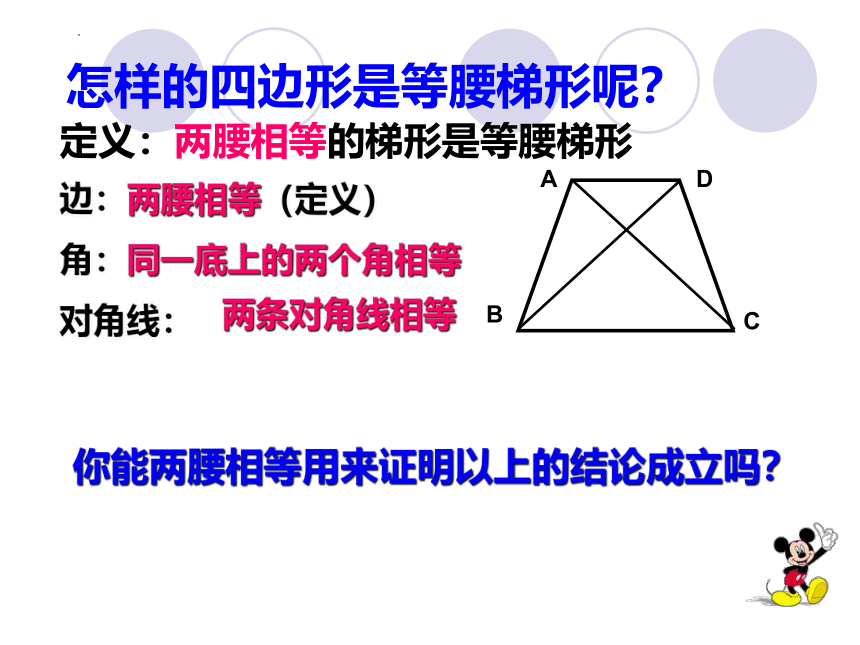
边:
两腰相等(定义)
角:
同一底上的两个角相等
对角线:
两条对角线相等
你能两腰相等用来证明以上的结论成立吗?
怎样的四边形是等腰梯形呢?
定义:两腰相等的梯形是等腰梯形
利用转化思维把梯形
转化为平行四边形,证
明同一底上的两个底角相等
A
B
C
D
E
1
随堂练习3
求证:等腰梯形同一底上的两底角相等
已知:AD∥BC,AB=CD
求证:∠B=∠C
利用转化思维把梯形
转化为矩形,证明同
一底上的两个底角相
等
A
B
C
D
E
F
A
B
C
D
等腰梯形的性质:
定理:等腰梯形在同一底上的两个角相等。
E
等腰梯形的判定:
定理:同一底上两个角相等
的梯形是等腰梯形.
已知:在梯形ABCD 中, AD ∥BC, ∠B=∠C
求证: AB=DC
利用转化思维把梯形转化为平行四边形,证明对角线相等
A
B
C
D
E
1
2
反过来,对角线相等
的梯形是等腰梯形吗?
怎么证明呢?
试一试
随堂练习4
比 一 比
(限时5分钟)
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等。( )
3、如图, ABCD中,BE=DF,图中有__对全等三角形。
A
D
C
B
E
4
ABCD
F
6
3
4、 中, ∠A比∠B大 30 , 则∠A=__,∠D=__.
ABCD
5、若A、B、C三点不共线,则以这三点为顶点的平行四边形有__个。
3
105°
75°
定理 平行四边形的对边平行.
定理 平行四边形的对边相等.
定理 平行四边形的对角相等.
定理 平行四边形的对角线互相平分.
定理 夹在平行线间的平行线段相等.
平行四边形的性质:
定理:等腰梯形在同一底上的两个角相等。
定理:等腰梯形的两条对角线相等.
定理:同一底上两个角相等的梯形是等腰梯形.
梯形的性质与判定:
定理:对角线相等的梯形是等腰梯形
作业
P76 习题1 2
谢谢!
平行四边形
怎么样的四边形是平行四边形
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
平行四边形有些什么性质?
A
B
C
D
平行四边形的性质
定理:平行四边形的对边平行.(定义)
定理:平行四边形的对边相等
定理:平行四边形的对角相等
定理:平行四边形的对角线互
相平分
A
B
C
D
O
你能用对边平行来证明对边相等和对角相等吗?
利用转化思维把四边形转 化为两个三角形的全等,证明对边和对角相等。
已知: AB∥CD ,AD∥BC
求证:AB=CD,BC=DA , ∠A= ∠C ∠B= ∠D
A
B
C
D
证明:∵AB∥CD
∴∠3=∠4
同理 ∠1=∠2
又∵ AC=CA
∴ ⊿ABC ≌⊿CDA(ASA)
∴ AB=CD BC=AD ∠B= ∠D
同理 ∠BAD= ∠BCD
1
2
3
4
怎样证明对角线互相平分?
A
B
C
D
O
利用转化思维把四边形转化为两个三角形的全等,再利用对边相等的性质证明对角线互相平分。
随堂练习1
已知: AB∥CD ,AD∥BC,
AC与BD相交于点O
求证:OA=OC,OB=OD
随堂练习2
定理:夹在两条平行线间的平行线段相等.
E
F
H
G
A
B
D
C
已知:如图,AB∥CD,EF∥GH.
求证:EF=GH
A
B
C
D
边:
两腰相等(定义)
角:
同一底上的两个角相等
对角线:
两条对角线相等
你能两腰相等用来证明以上的结论成立吗?
怎样的四边形是等腰梯形呢?
定义:两腰相等的梯形是等腰梯形
利用转化思维把梯形
转化为平行四边形,证
明同一底上的两个底角相等
A
B
C
D
E
1
随堂练习3
求证:等腰梯形同一底上的两底角相等
已知:AD∥BC,AB=CD
求证:∠B=∠C
利用转化思维把梯形
转化为矩形,证明同
一底上的两个底角相
等
A
B
C
D
E
F
A
B
C
D
等腰梯形的性质:
定理:等腰梯形在同一底上的两个角相等。
E
等腰梯形的判定:
定理:同一底上两个角相等
的梯形是等腰梯形.
已知:在梯形ABCD 中, AD ∥BC, ∠B=∠C
求证: AB=DC
利用转化思维把梯形转化为平行四边形,证明对角线相等
A
B
C
D
E
1
2
反过来,对角线相等
的梯形是等腰梯形吗?
怎么证明呢?
试一试
随堂练习4
比 一 比
(限时5分钟)
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等。( )
3、如图, ABCD中,BE=DF,图中有__对全等三角形。
A
D
C
B
E
4
ABCD
F
6
3
4、 中, ∠A比∠B大 30 , 则∠A=__,∠D=__.
ABCD
5、若A、B、C三点不共线,则以这三点为顶点的平行四边形有__个。
3
105°
75°
定理 平行四边形的对边平行.
定理 平行四边形的对边相等.
定理 平行四边形的对角相等.
定理 平行四边形的对角线互相平分.
定理 夹在平行线间的平行线段相等.
平行四边形的性质:
定理:等腰梯形在同一底上的两个角相等。
定理:等腰梯形的两条对角线相等.
定理:同一底上两个角相等的梯形是等腰梯形.
梯形的性质与判定:
定理:对角线相等的梯形是等腰梯形
作业
P76 习题1 2
谢谢!
