9.1.2 不等式的性质 说课课件 人教版数学七年级下册 41张PPT
文档属性
| 名称 | 9.1.2 不等式的性质 说课课件 人教版数学七年级下册 41张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 09:58:24 | ||
图片预览








文档简介
(共41张PPT)
不等式的性质
教学内容及要求
不等式的性质
简介
探索
教学方法选择
学法指导
教学过程分析
探索
不等式的概念
一、关于教学内容和要求的思考
用等式表示
相等关系
等式的性质
方程的解法
及应用
教材的地位和作用
探索
教材的地位和作用
不等式的性质是解不等式的重要依据,也是进行代数式变形的重要依据,对今后学习函数及其性质有着重大的作用
一、关于教学内容和要求的思考
教学目标
探索
知识技能:掌握不等式的性质,能应用不等式的性质解简单的一元一次不等式。
一、关于教学内容和要求的思考
教学目标
探索
数学思考:通过类比等式的性质,探索不等式的性质,体会不等式与等式的异同,初步掌握类比的思想方法,感受分类讨论的思想方法.
一、关于教学内容和要求的思考
教学目标
探索
解决问题:通过小组活动探索不等式的性质2、3,体会在解决问题过程中与他人合作的重要性。
一、关于教学内容和要求的思考
教学目标
探索
情感态度:认识通过观察、类比可以获得数学结论,体验数学活动充满着探索性和创造性。
一、关于教学内容和要求的思考
教学重点难点
探索
教学重点:探索、理解、应用不等式的性质,
教学难点:性质3的探索及应用。
一、关于教学内容和要求的思考
探索
二、教学方法的选择
教学方法的选择
引导——发现法
问题提出
性质探究
性质应用
设计意图:采取实验—观察—比较—猜测—验证—得出性质,调动学生积极性,在已有知识上建构新知识。
探索
学生自主探索
合作交流
得出性质
二、教学方法的选择
教学方法的选择
探索
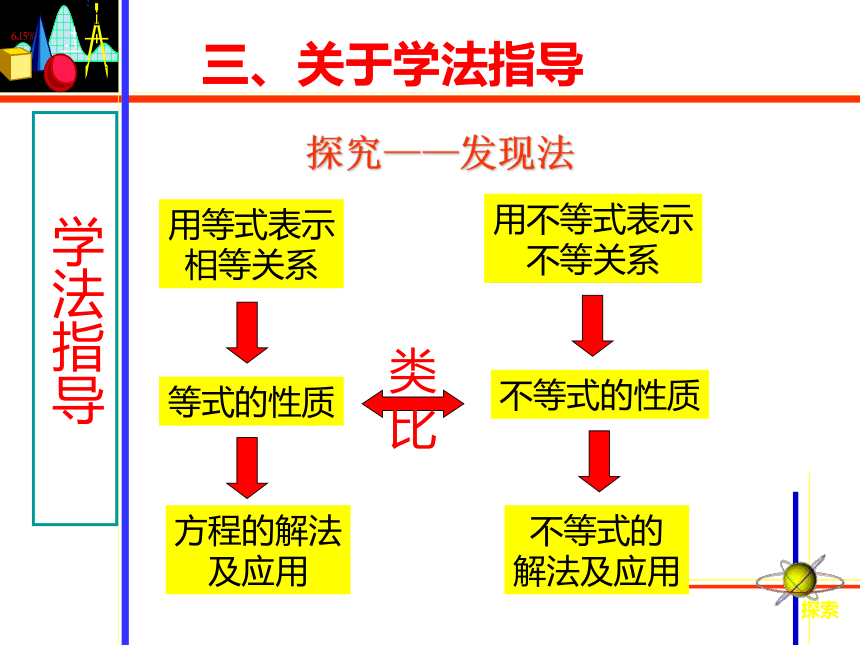
三、关于学法指导
学法指导
用等式表示
相等关系
等式的性质
方程的解法
及应用
用不等式表示
不等关系
不等式的性质
不等式的
解法及应用
类比
探究——发现法
探索
四 关于教学过程的设计
教学流程
提出问题 引出新知
观察思考 探索新知
应用性质 强化新知
总结归纳 反思提高
达标检测 布置作业
探索
四 关于教学过程的设计
提出问题 引出新知
直接想出不等式的解集:
探索
四 关于教学过程的设计
提出问题 引出新知
应用等式的性质,我们可以将方程进行变形,
解方程,为了解不等式,我们要将不等式进行
变形,提问:不等式是否有和等式类似的性质呢?
从而展开对不等式性质的探究.
探索
四 关于教学过程的设计
提出问题 引出新知
设计意图:从现有知识出发,展示新旧知识之
间的矛盾,引起学生的认识冲突,让学生在需
要中进入新知学习。
四、关于教学过程的设计:
观察思考 探索新知
用“>” 或“<”填空
观察并发现不等式的性质
1
四、关于教学过程的设计:
观察思考 探索新知
用“>” 或“<”填空
观察并发现不等式的性质
1
四、关于教学过程的设计:
探索
观察思考 探索新知
观察并发现不等式的性质
1
不等式性质1:
不等式两边加(或减)同一个数
(或式子),
不等号的方向不变
如果a>b,那么a±c>b±c
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
不等式的性质2:
不等式两边乘(或除以)同一个正数,
不等号的方向不变
如果a>b,c>0,那么a c>bc (或 ).
四、关于教学过程的设计:
探索
观察思考 探索新知
天平演示
根据初一学生理解、接受知识的特点,性质1和性质2可以用天平进行演示,从而加深理解。
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
对比不等式性质2,探究不等式性质3
充分体会性质2与性质3的区别 。
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
不等式的性质3:
不等式两边乘(或除以)同一个负数,
不等号的方向改变
如果a>b,c<0,那么a c<bc (或 ).
<
四、关于教学过程的设计:
探索
观察思考 探索新知
与等式性质对比
设计意图:对比不等式与等式的性质,体会不等式性质与等式性质的异同,体会类比的学习方法,引导学生得出:不等式的两边同时乘除同一个数时,不等号方向是否改变,要根据这个数的符号来确定.
四、关于教学过程的设计:
探索
应用性质 强化新知
四、关于教学过程的设计:
探索
应用性质 强化新知
例1、设a>b,用“>”或“<”填空:
(1)3a 3b;
(2)a+8 b+8
(3)-2a -2b
(4)2a 2b
(5)-3a+1 -3b+1
(6)a-x___ b-x
(7)a-b___ 0
四、关于教学过程的设计:
探索
应用性质 强化新知
例2、判断正误:
(1)∵a+8>4
∴a>-4 ( )
(2)∵3>2
∴a-3>a-2 ( )
(3)∵3>2
∴3a>2a( )
分类讨论的思想方法
四、关于教学过程的设计:
探索
应用性质 强化新知
1、若m>n,判断下列不等式是否正确?
(1)m-7(3)-5m>-5n. (4)
2、用“>”或“<”填空:
(1)如果a-1(2)如果3a>3b,那么a______b;
(3)如果-a<-b,那么a_______ b
(4)如果2a+1<2b+1,那么a______b.
加深学生对不等式性质的理解,为解不等式作铺垫.
四、关于教学过程的设计:
探索
应用性质 强化新知
从方程到不等式,类比等式基本性质的应用,学习
用不等式的性质解不等式的方法,体会不等式的解法
与方程的解法的异同,体会学习不等式性质的必要性。
x-5=-1 -2x=3
例3:利用不等式的性质解下列不等式 :
(1)x-5>-1 (2) -2x>3
四、关于教学过程的设计:
探索
应用性质 强化新知
通过练习,进一步巩固性质,突出重点突破难点。
尝试练习一(学生板演)
(1)x-1>2 (2)-x< (3) 4x≤3
巩固练习二 独立完成,班内交流
(1)x+3<-1 (2) 3x>27
(3)- x > 5 (4)4x<5x-6
四、关于教学过程的设计:
探索
应用性质 强化新知
解不等式是中考的热点,也是初中必会的知识点,二次根式、一元二次方程中字母的取值范围、以及函数中待定系数的取值范围等很多数学问题最终都转化为不等式这一数学模型,能否正确的求解,决定了学生最终能否得分,而学生往往在系数化为1,当系数为负数时,忘记不等号改变方向,导致失分,所以在不等式性质这一节要有意识的强化性质尤其是性质3 的应用.
四、关于教学过程的设计:
探索
应用性质 强化新知
类比一元一次方程的解法学习一元一
次不等式的解法,让学生非常清楚地
看到不等式的解法与方程的解法只是
最后系数化为1不同,其它的步骤是
相同的,强调最后一步“负变,正不变”.
四、关于教学过程的设计:
总结归纳、反思提高
数学知识:不等式的性质,应用不等式的性质对不等式进行变形.
数学思想方法:类比、分类讨论
注意问题:应用不等式的性质3时不等号的处理.
探索
一方面在回顾本节主要内容的同时,培养了学生归纳总结和语言表达能力,另一方面树立了学生学习数学的自信心和学习的勇气。
四、关于教学过程的设计:
探索
1、已知a<b,用“<”或“>”填空:
(1)a-34____b-34 (2)2a____2b
(3)-3a____-3b (4)b-a ____0
2、将下列不等式化成“x>a”或“x<a” 的形式:
(1)x+4<-3 (2)9x >45
(3)- >13 (4)3x<5x-6
设计意图:及时反馈,掌握情况。
达标检测 布置作业
四、关于教学过程的设计:
达标检测 布置作业
探索
必做:
1.看书:P123——125.
(目的:让学生养成复习的好习惯).
2.课本P128,3-7题.
(目的:进一步巩固不等式性质的应用)
选做:若m,n为有理数,解关于x的不等式:
(-m2-1)x>n
设计意图:利用选做题引导学生对数学知识进一步的思考,坚持给学生一些兴趣题或提高题,可以很好的激发学生学数学用数学的兴趣,同时提高了学生应用数学解决问题的能力。
谢谢大家
再见
不等式的性质
教学内容及要求
不等式的性质
简介
探索
教学方法选择
学法指导
教学过程分析
探索
不等式的概念
一、关于教学内容和要求的思考
用等式表示
相等关系
等式的性质
方程的解法
及应用
教材的地位和作用
探索
教材的地位和作用
不等式的性质是解不等式的重要依据,也是进行代数式变形的重要依据,对今后学习函数及其性质有着重大的作用
一、关于教学内容和要求的思考
教学目标
探索
知识技能:掌握不等式的性质,能应用不等式的性质解简单的一元一次不等式。
一、关于教学内容和要求的思考
教学目标
探索
数学思考:通过类比等式的性质,探索不等式的性质,体会不等式与等式的异同,初步掌握类比的思想方法,感受分类讨论的思想方法.
一、关于教学内容和要求的思考
教学目标
探索
解决问题:通过小组活动探索不等式的性质2、3,体会在解决问题过程中与他人合作的重要性。
一、关于教学内容和要求的思考
教学目标
探索
情感态度:认识通过观察、类比可以获得数学结论,体验数学活动充满着探索性和创造性。
一、关于教学内容和要求的思考
教学重点难点
探索
教学重点:探索、理解、应用不等式的性质,
教学难点:性质3的探索及应用。
一、关于教学内容和要求的思考
探索
二、教学方法的选择
教学方法的选择
引导——发现法
问题提出
性质探究
性质应用
设计意图:采取实验—观察—比较—猜测—验证—得出性质,调动学生积极性,在已有知识上建构新知识。
探索
学生自主探索
合作交流
得出性质
二、教学方法的选择
教学方法的选择
探索
三、关于学法指导
学法指导
用等式表示
相等关系
等式的性质
方程的解法
及应用
用不等式表示
不等关系
不等式的性质
不等式的
解法及应用
类比
探究——发现法
探索
四 关于教学过程的设计
教学流程
提出问题 引出新知
观察思考 探索新知
应用性质 强化新知
总结归纳 反思提高
达标检测 布置作业
探索
四 关于教学过程的设计
提出问题 引出新知
直接想出不等式的解集:
探索
四 关于教学过程的设计
提出问题 引出新知
应用等式的性质,我们可以将方程进行变形,
解方程,为了解不等式,我们要将不等式进行
变形,提问:不等式是否有和等式类似的性质呢?
从而展开对不等式性质的探究.
探索
四 关于教学过程的设计
提出问题 引出新知
设计意图:从现有知识出发,展示新旧知识之
间的矛盾,引起学生的认识冲突,让学生在需
要中进入新知学习。
四、关于教学过程的设计:
观察思考 探索新知
用“>” 或“<”填空
观察并发现不等式的性质
1
四、关于教学过程的设计:
观察思考 探索新知
用“>” 或“<”填空
观察并发现不等式的性质
1
四、关于教学过程的设计:
探索
观察思考 探索新知
观察并发现不等式的性质
1
不等式性质1:
不等式两边加(或减)同一个数
(或式子),
不等号的方向不变
如果a>b,那么a±c>b±c
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
2
不等式的性质2:
不等式两边乘(或除以)同一个正数,
不等号的方向不变
如果a>b,c>0,那么a c>bc (或 ).
四、关于教学过程的设计:
探索
观察思考 探索新知
天平演示
根据初一学生理解、接受知识的特点,性质1和性质2可以用天平进行演示,从而加深理解。
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
用“>” 或“<”填空
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
对比不等式性质2,探究不等式性质3
充分体会性质2与性质3的区别 。
四、关于教学过程的设计:
探索
观察思考 探索新知
探究不等式的性质
3
不等式的性质3:
不等式两边乘(或除以)同一个负数,
不等号的方向改变
如果a>b,c<0,那么a c<bc (或 ).
<
四、关于教学过程的设计:
探索
观察思考 探索新知
与等式性质对比
设计意图:对比不等式与等式的性质,体会不等式性质与等式性质的异同,体会类比的学习方法,引导学生得出:不等式的两边同时乘除同一个数时,不等号方向是否改变,要根据这个数的符号来确定.
四、关于教学过程的设计:
探索
应用性质 强化新知
四、关于教学过程的设计:
探索
应用性质 强化新知
例1、设a>b,用“>”或“<”填空:
(1)3a 3b;
(2)a+8 b+8
(3)-2a -2b
(4)2a 2b
(5)-3a+1 -3b+1
(6)a-x___ b-x
(7)a-b___ 0
四、关于教学过程的设计:
探索
应用性质 强化新知
例2、判断正误:
(1)∵a+8>4
∴a>-4 ( )
(2)∵3>2
∴a-3>a-2 ( )
(3)∵3>2
∴3a>2a( )
分类讨论的思想方法
四、关于教学过程的设计:
探索
应用性质 强化新知
1、若m>n,判断下列不等式是否正确?
(1)m-7
2、用“>”或“<”填空:
(1)如果a-1
(3)如果-a<-b,那么a_______ b
(4)如果2a+1<2b+1,那么a______b.
加深学生对不等式性质的理解,为解不等式作铺垫.
四、关于教学过程的设计:
探索
应用性质 强化新知
从方程到不等式,类比等式基本性质的应用,学习
用不等式的性质解不等式的方法,体会不等式的解法
与方程的解法的异同,体会学习不等式性质的必要性。
x-5=-1 -2x=3
例3:利用不等式的性质解下列不等式 :
(1)x-5>-1 (2) -2x>3
四、关于教学过程的设计:
探索
应用性质 强化新知
通过练习,进一步巩固性质,突出重点突破难点。
尝试练习一(学生板演)
(1)x-1>2 (2)-x< (3) 4x≤3
巩固练习二 独立完成,班内交流
(1)x+3<-1 (2) 3x>27
(3)- x > 5 (4)4x<5x-6
四、关于教学过程的设计:
探索
应用性质 强化新知
解不等式是中考的热点,也是初中必会的知识点,二次根式、一元二次方程中字母的取值范围、以及函数中待定系数的取值范围等很多数学问题最终都转化为不等式这一数学模型,能否正确的求解,决定了学生最终能否得分,而学生往往在系数化为1,当系数为负数时,忘记不等号改变方向,导致失分,所以在不等式性质这一节要有意识的强化性质尤其是性质3 的应用.
四、关于教学过程的设计:
探索
应用性质 强化新知
类比一元一次方程的解法学习一元一
次不等式的解法,让学生非常清楚地
看到不等式的解法与方程的解法只是
最后系数化为1不同,其它的步骤是
相同的,强调最后一步“负变,正不变”.
四、关于教学过程的设计:
总结归纳、反思提高
数学知识:不等式的性质,应用不等式的性质对不等式进行变形.
数学思想方法:类比、分类讨论
注意问题:应用不等式的性质3时不等号的处理.
探索
一方面在回顾本节主要内容的同时,培养了学生归纳总结和语言表达能力,另一方面树立了学生学习数学的自信心和学习的勇气。
四、关于教学过程的设计:
探索
1、已知a<b,用“<”或“>”填空:
(1)a-34____b-34 (2)2a____2b
(3)-3a____-3b (4)b-a ____0
2、将下列不等式化成“x>a”或“x<a” 的形式:
(1)x+4<-3 (2)9x >45
(3)- >13 (4)3x<5x-6
设计意图:及时反馈,掌握情况。
达标检测 布置作业
四、关于教学过程的设计:
达标检测 布置作业
探索
必做:
1.看书:P123——125.
(目的:让学生养成复习的好习惯).
2.课本P128,3-7题.
(目的:进一步巩固不等式性质的应用)
选做:若m,n为有理数,解关于x的不等式:
(-m2-1)x>n
设计意图:利用选做题引导学生对数学知识进一步的思考,坚持给学生一些兴趣题或提高题,可以很好的激发学生学数学用数学的兴趣,同时提高了学生应用数学解决问题的能力。
谢谢大家
再见
