数与形中的生活问题(课件)人教版六年级数学上册(共15张PPT)
文档属性
| 名称 | 数与形中的生活问题(课件)人教版六年级数学上册(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 586.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
数与形中的生活问题
人教版六年级(上)数学学科
【例1】
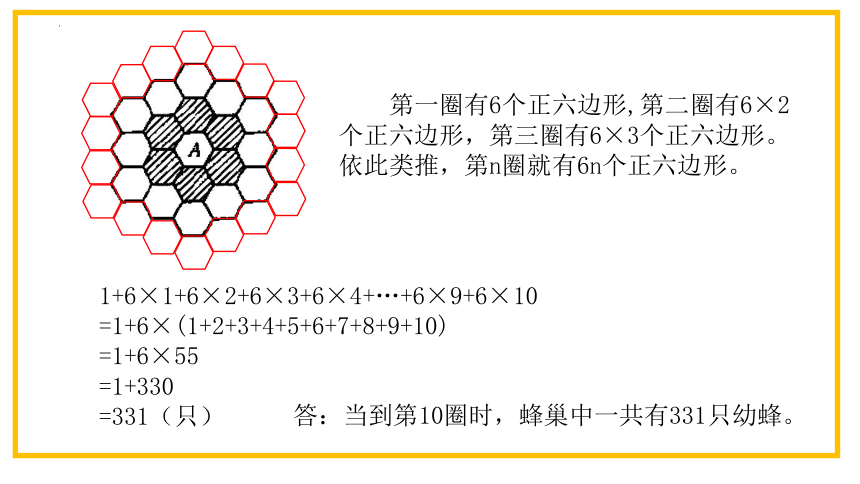
如图是蜂巢的一部分,已知正六边形A中有一只幼蜂。在A周围有6个同样的正六边形(阴影部分),围成第l圈;在第1圈外面又有12个同样的正六边形,围成第2圈。每个正六边形中都有一只幼蜂。按此类推,当到第10圈时,蜂巢中一共有多少只幼蜂
第一圈有6个正六边形,第二圈有6×2个正六边形,第三圈有6×3个正六边形。依此类推,第n圈就有6n个正六边形。
1+6×1+6×2+6×3+6×4+…+6×9+6×10
=1+6×(1+2+3+4+5+6+7+8+9+10)
=1+6×55
=1+330
=331(只)
答:当到第10圈时,蜂巢中一共有331只幼蜂。
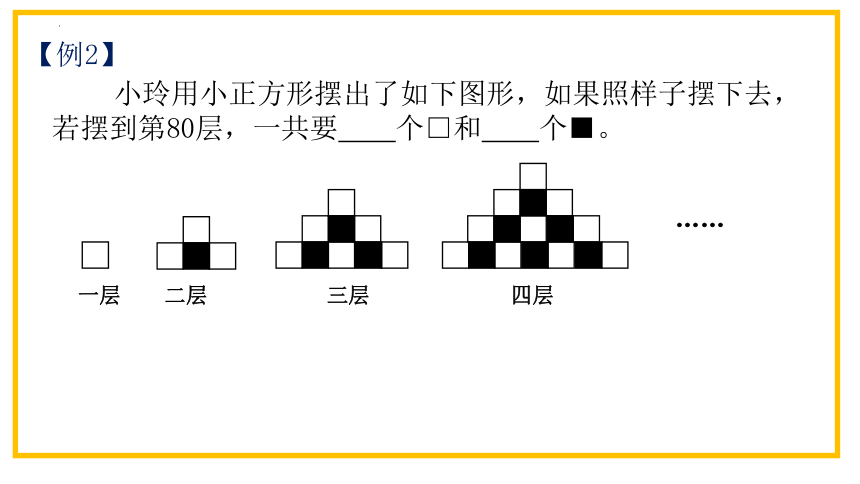
【例2】
小玲用小正方形摆出了如下图形,如果照样子摆下去,若摆到第80层,一共要 个□和 个■。
一层 二层 三层 四层
……
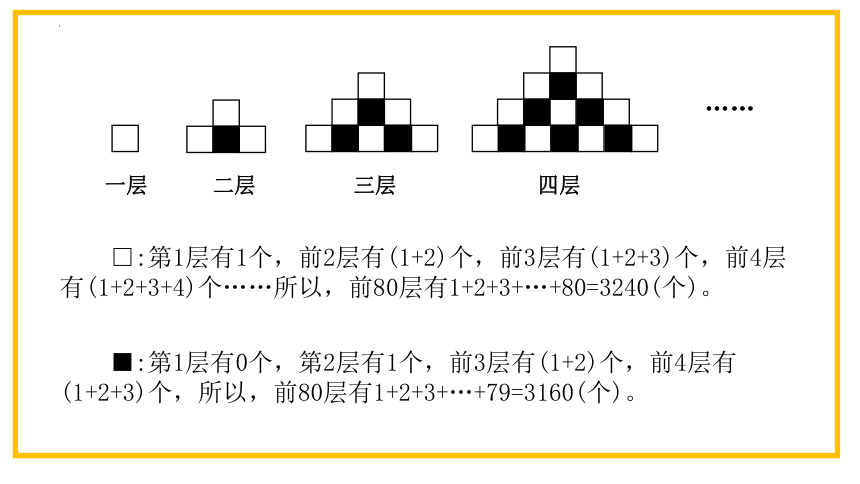
一层 二层 三层 四层
……
□:第1层有1个,前2层有(1+2)个,前3层有(1+2+3)个,前4层有(1+2+3+4)个……所以,前80层有1+2+3+…+80=3240(个)。
■:第1层有0个,第2层有1个,前3层有(1+2)个,前4层有(1+2+3)个,所以,前80层有1+2+3+…+79=3160(个)。
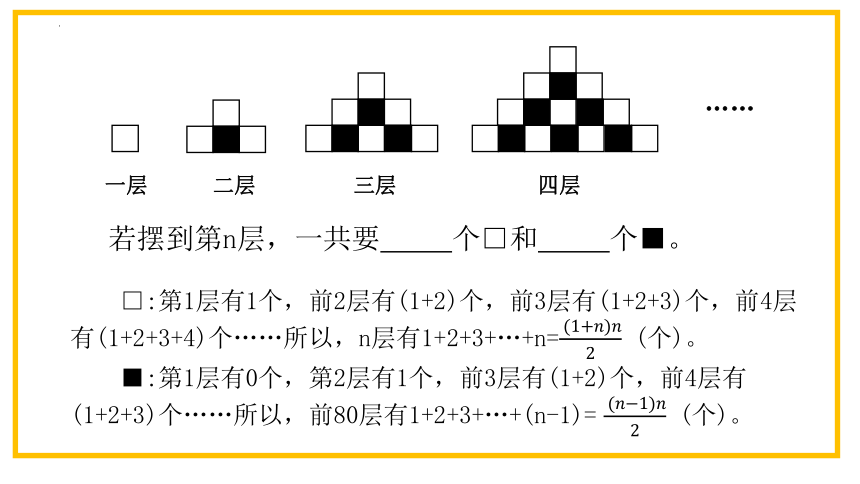
一层 二层 三层 四层
……
□:第1层有1个,前2层有(1+2)个,前3层有(1+2+3)个,前4层有(1+2+3+4)个……所以,n层有1+2+3+…+n= (个)。
■:第1层有0个,第2层有1个,前3层有(1+2)个,前4层有(1+2+3)个……所以,前80层有1+2+3+…+(n-1)= (个)。
若摆到第n层,一共要 个□和 个■。
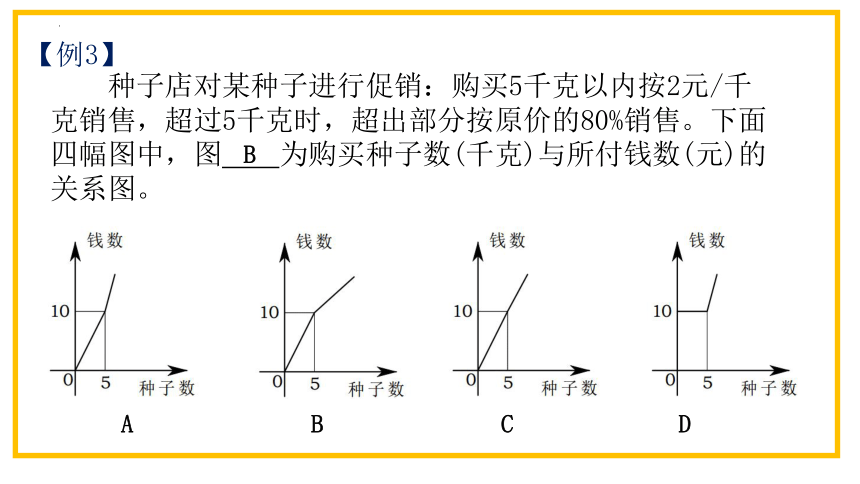
【例3】
种子店对某种子进行促销:购买5千克以内按2元/千克销售,超过5千克时,超出部分按原价的80%销售。下面四幅图中,图 为购买种子数(千克)与所付钱数(元)的关系图。
B
A B C D
【例4】
冬冬从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示。放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是 分钟。
上学时:
上坡速度:400÷4=100 (米/分)
下坡速度:(1200-400)÷(8-4)=200(米/分)
平路速度:(2000-1200)÷(13-8)=160(米/分)
回家时:
平路时间800÷160=5(分钟)
上坡时间:800÷100=8(分钟)
下坡时间:400÷200=2(分钟)
总时间:5+8+2=15(分钟)
答:他从学校到家需要的时间是15分钟。
【练一练】
小强从家出发到学校,以每小时4千米速度前进,但一会他记起数学课本忘在家里,于是以每小时5千米的速度往家赶,为了不迟到,他不得不再以7千米的速度奔向学校,下列图中能正确地表达小强上学情况的是( )。
A B C D
【练一练】
小强用棱长为1的小立方体粘合而成的大立方体,从正面、侧面、上面看到的视图均如下图所示,那么黏成这个大立方体最多需要( )个小立方体。
第1层
第2层
第4层
第3层
用棱长为1的正方体黏合而成的大立方体,由上而下共5层,打了穿透的“十”字孔之后,从上面第一层到最下面一层,剩下的小立方体的个数依次是:20,16,4,16,20。
20+16+4+16+20=76(个)
某公交公司的公共汽车和出租车每天从甲地出发往返于甲、乙两地,出租车比公共汽车多往返一趟,下图表示出租车距甲地的路程y(单位:千米)与所用时间x(单位:小时)的图像。已知公共汽车比出租车晚1小时出发,到达乙地后休息2小时,然后按原路原速返回,结果比出租车最后一次返回甲地早1小时。
(1)求两车在途中相遇的次数。
(2)求两车最后一次相遇时,距离甲地的路程。
【练一练】
(1)如图可知,两车在途中相遇2次。
(2)出租车每天往返甲、乙两地2次,于是可知公共汽车每天往返甲、乙两地1次。又因为公共汽车比出租车晚1小时出发,提前1小时返回,并且到达乙地后休息2小时,即公共汽车往返甲、乙两地一次共需8-1-1-2=4(小时),由图可知出租车往返甲、乙两地一次也需4小时,即公共汽车和出租车的速度相同,即150÷2=75(千米/时)。由图可知:
两车最后一次相遇时距离甲地(150-75)÷(75+75)×75+75=112.5(千米)。所以,两车最后一次相遇时距离甲地的路程为112.5千米。
同学们
再见!
数与形中的生活问题
人教版六年级(上)数学学科
【例1】
如图是蜂巢的一部分,已知正六边形A中有一只幼蜂。在A周围有6个同样的正六边形(阴影部分),围成第l圈;在第1圈外面又有12个同样的正六边形,围成第2圈。每个正六边形中都有一只幼蜂。按此类推,当到第10圈时,蜂巢中一共有多少只幼蜂
第一圈有6个正六边形,第二圈有6×2个正六边形,第三圈有6×3个正六边形。依此类推,第n圈就有6n个正六边形。
1+6×1+6×2+6×3+6×4+…+6×9+6×10
=1+6×(1+2+3+4+5+6+7+8+9+10)
=1+6×55
=1+330
=331(只)
答:当到第10圈时,蜂巢中一共有331只幼蜂。
【例2】
小玲用小正方形摆出了如下图形,如果照样子摆下去,若摆到第80层,一共要 个□和 个■。
一层 二层 三层 四层
……
一层 二层 三层 四层
……
□:第1层有1个,前2层有(1+2)个,前3层有(1+2+3)个,前4层有(1+2+3+4)个……所以,前80层有1+2+3+…+80=3240(个)。
■:第1层有0个,第2层有1个,前3层有(1+2)个,前4层有(1+2+3)个,所以,前80层有1+2+3+…+79=3160(个)。
一层 二层 三层 四层
……
□:第1层有1个,前2层有(1+2)个,前3层有(1+2+3)个,前4层有(1+2+3+4)个……所以,n层有1+2+3+…+n= (个)。
■:第1层有0个,第2层有1个,前3层有(1+2)个,前4层有(1+2+3)个……所以,前80层有1+2+3+…+(n-1)= (个)。
若摆到第n层,一共要 个□和 个■。
【例3】
种子店对某种子进行促销:购买5千克以内按2元/千克销售,超过5千克时,超出部分按原价的80%销售。下面四幅图中,图 为购买种子数(千克)与所付钱数(元)的关系图。
B
A B C D
【例4】
冬冬从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示。放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是 分钟。
上学时:
上坡速度:400÷4=100 (米/分)
下坡速度:(1200-400)÷(8-4)=200(米/分)
平路速度:(2000-1200)÷(13-8)=160(米/分)
回家时:
平路时间800÷160=5(分钟)
上坡时间:800÷100=8(分钟)
下坡时间:400÷200=2(分钟)
总时间:5+8+2=15(分钟)
答:他从学校到家需要的时间是15分钟。
【练一练】
小强从家出发到学校,以每小时4千米速度前进,但一会他记起数学课本忘在家里,于是以每小时5千米的速度往家赶,为了不迟到,他不得不再以7千米的速度奔向学校,下列图中能正确地表达小强上学情况的是( )。
A B C D
【练一练】
小强用棱长为1的小立方体粘合而成的大立方体,从正面、侧面、上面看到的视图均如下图所示,那么黏成这个大立方体最多需要( )个小立方体。
第1层
第2层
第4层
第3层
用棱长为1的正方体黏合而成的大立方体,由上而下共5层,打了穿透的“十”字孔之后,从上面第一层到最下面一层,剩下的小立方体的个数依次是:20,16,4,16,20。
20+16+4+16+20=76(个)
某公交公司的公共汽车和出租车每天从甲地出发往返于甲、乙两地,出租车比公共汽车多往返一趟,下图表示出租车距甲地的路程y(单位:千米)与所用时间x(单位:小时)的图像。已知公共汽车比出租车晚1小时出发,到达乙地后休息2小时,然后按原路原速返回,结果比出租车最后一次返回甲地早1小时。
(1)求两车在途中相遇的次数。
(2)求两车最后一次相遇时,距离甲地的路程。
【练一练】
(1)如图可知,两车在途中相遇2次。
(2)出租车每天往返甲、乙两地2次,于是可知公共汽车每天往返甲、乙两地1次。又因为公共汽车比出租车晚1小时出发,提前1小时返回,并且到达乙地后休息2小时,即公共汽车往返甲、乙两地一次共需8-1-1-2=4(小时),由图可知出租车往返甲、乙两地一次也需4小时,即公共汽车和出租车的速度相同,即150÷2=75(千米/时)。由图可知:
两车最后一次相遇时距离甲地(150-75)÷(75+75)×75+75=112.5(千米)。所以,两车最后一次相遇时距离甲地的路程为112.5千米。
同学们
再见!
