2022-2023学年湖南省湘潭市湘潭子敬中学等三校九年级(下)开学数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年湖南省湘潭市湘潭子敬中学等三校九年级(下)开学数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 413.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 10:45:41 | ||
图片预览



文档简介
绝密★启用前
2022-2023学年湖南省湘潭市湘潭子敬中学等三校九年级(下)开学数学试卷
学校:___________姓名:___________班级:___________考号:___________
得分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
1. 用求根公式解一元二次方程时,,的值是( )
A. ,, B. ,,
C. ,, D. ,,
2. 某城市调查组为了解该城市的森林覆盖率,随机抽取面积为的土地进行调查后,估算出森林覆盖率为若该城市所占面积为,据此估算出该城市森林所占面积为( )
A. B. C. D.
3. 如图,若直线,且::,,则( )
A.
B.
C.
D.
4. 为了了解学校名学生周末完成作业所用时间,数学兴趣小组随机抽取了名学生进行了调查,在这个问题中,样本容量是( )
A. B. 被抽查的名学生 C. D. 名学生
5. 已知∽,且,,若的面积为,则的面积为( )
A. B. C. D. 无法计算
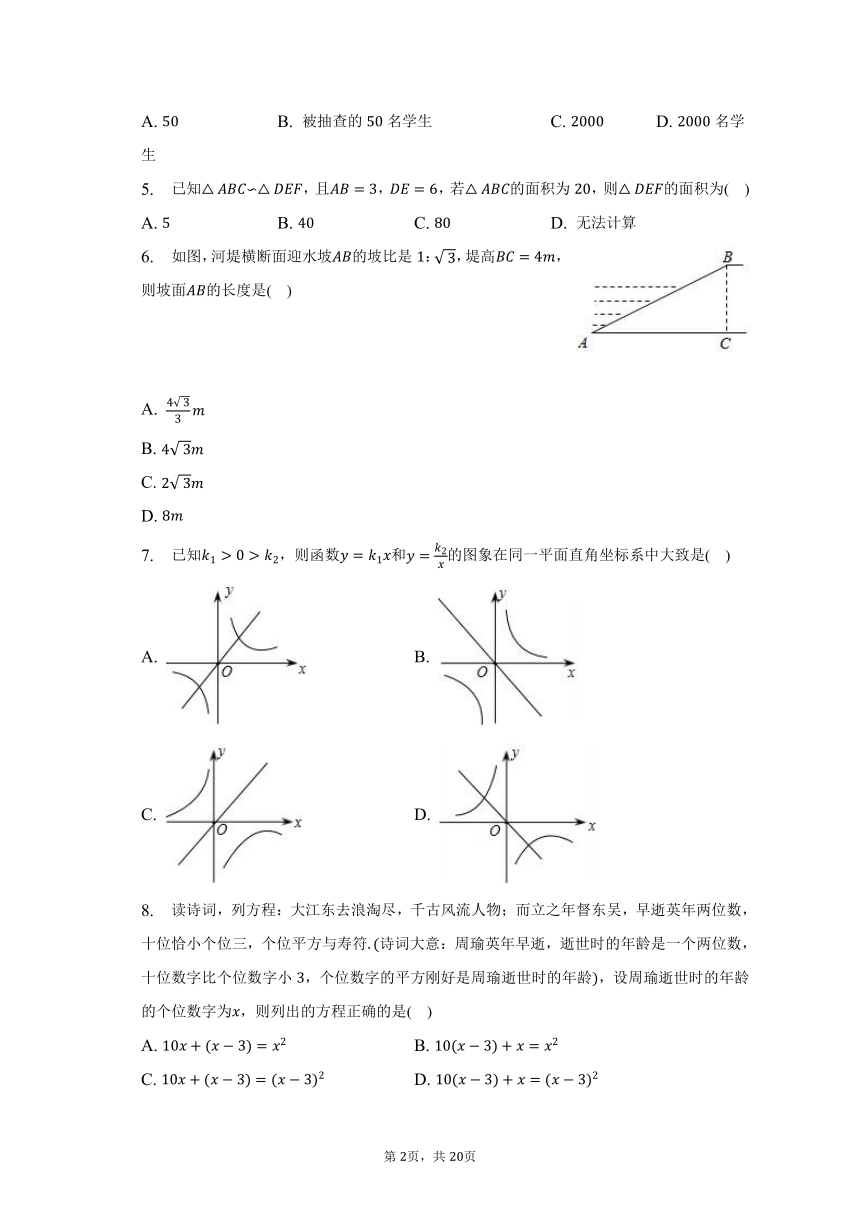
6. 如图,河堤横断面迎水坡的坡比是:,堤高,则坡面的长度是( )
A.
B.
C.
D.
7. 已知,则函数和的图象在同一平面直角坐标系中大致是( )
A. B.
C. D.
8. 读诗词,列方程:大江东去浪淘尽,千古风流人物;而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符诗词大意:周瑜英年早逝,逝世时的年龄是一个两位数,十位数字比个位数字小,个位数字的平方刚好是周瑜逝世时的年龄,设周瑜逝世时的年龄的个位数字为,则列出的方程正确的是( )
A. B.
C. D.
9. 对于反比例函数,下列说法正确的是( )
A. 它的图象分布在第一、三象限 B. 它的图象分布在第二、四象限
C. 点在函数图象上 D. 当时,的值随的增大而增大
10. 如图,在直角三角形中,,,则下列结论正确的是( )
A.
B.
C.
D. 若,则
11. 若关于的方程有两个相等的实数解,则的值可能为( )
A. B. C. D.
12. 如图,是边上一点,添加一个条件后,仍不能使∽的是( )
A.
B.
C.
D.
13. 若,则 .
14. 如图,点在函数的图象上,过点作轴于点,则的面积为______.
15. 甲、乙、丙、丁四个小组参加体育测试,他们成绩的平均分均为分,方差分别为:,,,,则这四个小组体育测试成绩最稳定的是______ 组
16. 请写出一个满足下列条件的一元二次方程:二次项系数为,且两根之和为正数,两根之积为负数你所写的一元二次方程是______ .
17. 计算:.
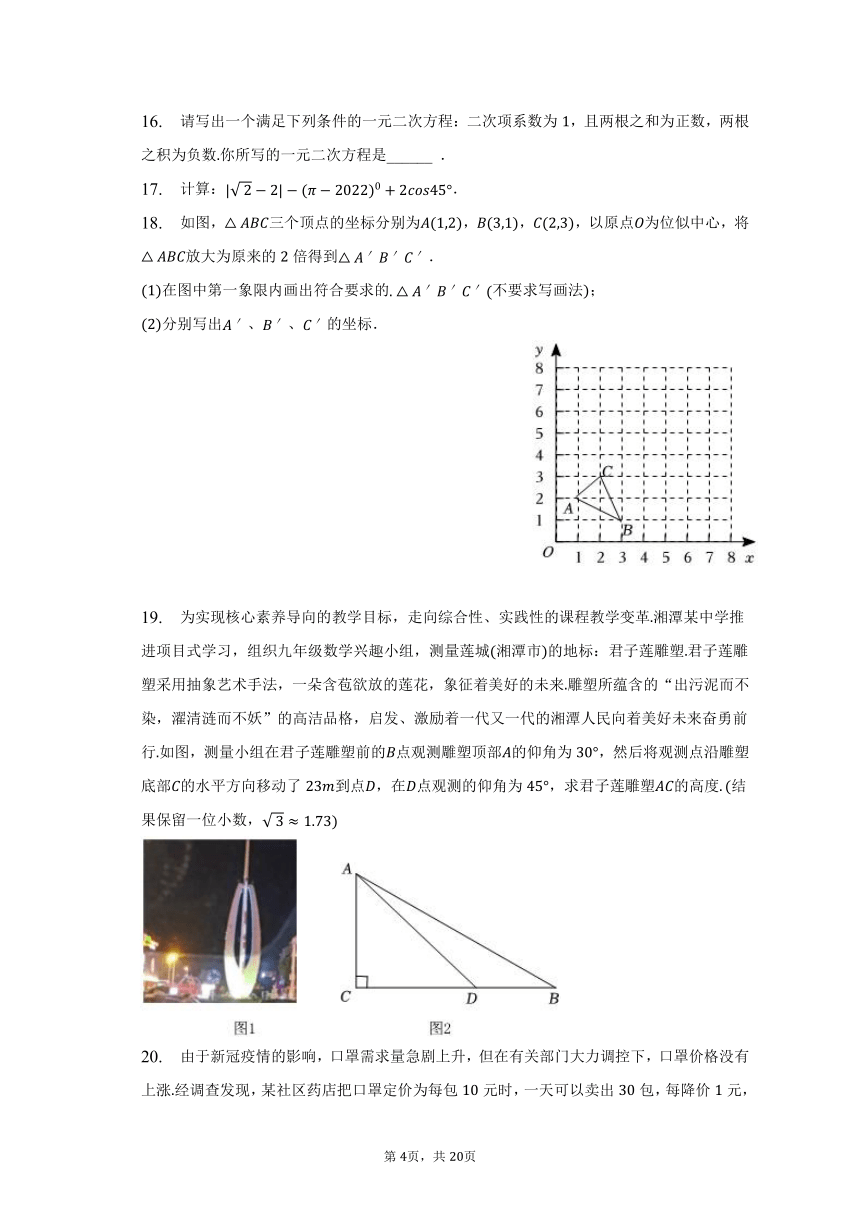
18. 如图,三个顶点的坐标分别为,,,以原点为位似中心,将放大为原来的倍得到.
在图中第一象限内画出符合要求的不要求写画法;
分别写出、、的坐标.
19. 为实现核心素养导向的教学目标,走向综合性、实践性的课程教学变革湘潭某中学推进项目式学习,组织九年级数学兴趣小组,测量莲城湘潭市的地标:君子莲雕塑君子莲雕塑采用抽象艺术手法,一朵含苞欲放的莲花,象征着美好的未来雕塑所蕴含的“出污泥而不染,濯清涟而不妖”的高洁品格,启发、激励着一代又一代的湘潭人民向着美好未来奋勇前行如图,测量小组在君子莲雕塑前的点观测雕塑顶部的仰角为,然后将观测点沿雕塑底部的水平方向移动了到点,在点观测的仰角为,求君子莲雕塑的高度结果保留一位小数,
20. 由于新冠疫情的影响,口罩需求量急剧上升,但在有关部门大力调控下,口罩价格没有上涨经调查发现,某社区药店把口罩定价为每包元时,一天可以卖出包,每降价元,可以多卖出包如果该药店想一天获得元口罩销售额,并且尽可能让顾客获得更大的优惠,应该降价多少元?
21. 如图,一次函数的图象与反比例函数为常数,且的图象交于、两点.
求反比例函数的表达式;
求点的坐标.
22. 如图,在 中,是边上的任意点不与重合,连接交于点.
求证:∽;
若是的中点,且,求的长度.
23. “双减”政策实施以来,越来越重视课堂效率了,比如有效的预习可以大幅度提高课堂效率八年级班数学学习兴趣小组为了了解全校八年级学生的预习情况,对该校八年级学生每天的课前预习时间进行了抽样调查,并将得到的数据分成组,下面是未完成的频数、频率分布表和扇形图.
组别 课前预习时间 频数人数 频率
请根据图表中的信息,回答下列问题:
表中的 ______ , ______ ;
试计算第组人数所对应的扇形圆心角的度数;
该校八年级有名学生,请估计这些学生中每天课前预习时不少于的学生人数.
24. 近期,流感进入发病高峰期,某校为预防流感,对教室进行熏药消毒,测得药物燃烧后室内每立方米空气中的含药量与时间之间的函数关系如图所示,已知药物燃烧时,满足;药物燃烧后,与成反比例,现测得药物分钟燃毕,此时室内每立方米空气中的含药量为请根据图中所提供的信息,解决下列问题:
求的值,并求当时,与的函数表达式;
研究表明,当空气中每立方米的含药量不低于毫克且持续时间不低于分钟时,才能有效杀灭空气中的病菌,则此次消毒是否有效?请计算说明.
25. 在矩形中,,,点从点开始沿边向终点以的速度移动,与此同时,点从点开始沿向终点以的速度移动,如果,分别从,同时出发,当点运动到点时,两点停止运动设运动时间为秒.
填空:运动时间的取值范围足______ .
是否存在的值,使得的长度等于?若存在,请求出此时的值,若不存在,请说明理由.
是否存在的值,使得五边形的面积等于?若存在,请求出此时的值,若不存在,请说明理由.
26. 如图,在中,,,,点是的中点,过点作交与点.
填空: ______ , ______ .
如图,将绕点顺时针旋转,连接、,交于点,、所在直线交于点,则:
试判断,在旋转过程中,是否为定值,并给出理由;
当为直角三角形时,求的长度.
答案和解析
1.【答案】
【解析】解:,
,
,,,
故选:.
先将方程化为一般形式,然后即可写出、、,本题得以解决.
本题考查解一元二次方程的一般形式、解一元二次方程公式法,解答本题的关键是明确一元二次方程的一般形式.
2.【答案】
【解析】解:由样本可知:该城市森林覆盖率是,
该城市森林所占面积为:,
故选:.
用样本估计出该城市森林覆盖率,计算即可.
本题考查的是样本去估计总体,根据样本估计出该城市森林覆盖率是解题的关键.
3.【答案】
【解析】解:直线,且::,
,
,
,
故选:.
由平行线分线段成比例定理得,则,即可得出结论.
本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.熟练掌握平行线分线段成比例定理是解题的关键
4.【答案】
【解析】解:为了了解学校名学生周末完成作业所用时间,数学兴趣小组随机抽取了名学生进行了调查,在这个问题中,样本容量是.
故选:.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
本题主要考查样本容量的含义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
5.【答案】
【解析】解:∽,,,
:::,
面积的比为:,
的面积为,
的面积为,
故选:.
根据相似三角形的面积比等于相似比的平方计算,得到答案.
本题考查的是相似三角形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
6.【答案】
【解析】解:因为坡度:,
,
,
.
故选D.
根据坡度坡角定义即可求出结果.
本题考查解直角三角形的应用.
7.【答案】
【解析】解:,
函数的图象分布在第一、三象限,反比例的图象分布在第二、四象限.
故选:.
根据反比例函数,当时,图象分布在第二、四象限和一次函数图象与系数的关系进行判断;
本题考查了一次函数图象和反比例函数的图象:反比例函数为双曲线,当时,图象分布在第一、三象限;当时,图象分布在第二、四象限.
8.【答案】
【解析】解:周瑜逝世时的年龄的个位数字为,且十位数字比个位数字小,
周瑜逝世时的年龄的十位数字为.
根据题意得:.
故选:.
由周瑜逝世时的年龄的十位数字与个位数字间的关系,可得出周瑜逝世时的年龄的十位数字为,结合周瑜逝世时的年龄的个位数字的平方刚好是周瑜逝世时的年龄,即可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
9.【答案】
【解析】解:反比例函数,
,该函数的图象分布在第一、三象限,故选项A符合题意,选项B不符合题意;
当时,,故点在函数图象上,故选项C符合题意;
当时,随的增大而减小,故选项D不符合题意.
故选:.
根据反比例函数的解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
本题考查反比例函数的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.
10.【答案】
【解析】解:由于,设,则,由勾股定理得,
,
,选项A不符合题意;
,选项B符合题意;
,选项C符合题意;
若,即,则,因此选项D符合题意.
故选:.
根据锐角三角函数的定义以及勾股定理逐项进行判断即可.
本题考查同角三角函数的关系,掌握锐角三角函数的定义以及勾股定理是正确解答的前提.
11.【答案】
【解析】解:由题意可知:,
,
故选:.
根据根的判别式即可求出答案.
本题考查了一元二次方程的根的判别式:当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根.
12.【答案】
【解析】解:、当时,再由,可得出∽,故此选项不合题意;
B、当时,再由,可得出∽,故此选项不合题意;
C、当时,无法得出∽,故此选项符合题意;
D、当时,即,再由,可得出∽,故此选项不合题意;
故选:.
直接利用相似三角形的判定方法分别分析得出答案.
此题主要考查了相似三角形的判定,正确掌握相似三角形的判定方法是解题关键.
13.【答案】
【解析】解:,根据等式的性质,得,
则,
故答案为:.
根据题意,即可得出答案.
本题考查等式的性质,属于基础题.
14.【答案】
【解析】解:由的几何意义可知:的面积为,
当时,
的面积为:
故答案为:
根据反比例函数的几何意义可知:的面积为,代入的值即可求出答案.
本题考查反比例函数系数的几何意义,解题的关键是根据三角形的面积为求解,本题属于基础题型.
15.【答案】甲
【解析】解:,,,,
,
这四个小组体育测试成绩最稳定的是甲组,
故答案为:甲.
根据方差的意义即可得出答案.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则与平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
16.【答案】答案不唯一
【解析】解:二次项系数为,且两根之和为正数,两根之积为负数.
这样的方程为.
故答案为:答案不唯一.
根据两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除二次项系数,直接写出一个方程即可,答案不唯一.
本题考查了一元二次方程根与系数的关系,熟记两根之和与两根之积是解题的关键.
17.【答案】解:原式
.
【解析】分别根据绝对值的性质,零指数幂及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行解答即可.
本题考查的是实数的运算,熟知绝对值的性质,零指数幂的运算法则,特殊角的三角函数值是解题的关键.
18.【答案】解:如图,为所作;,,.
【解析】利用关于以原点为位似中心的对应点的坐标特征写出点、、的坐标,然后描点即可.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
19.【答案】解:设君子莲雕塑的高度为米,
在中,,,
是等腰直角三角形,
米,
在中,米,,
,
,
解得:,
经检验,是原方程的解,且符合题意,
答:君子莲雕塑的高度约为米.
【解析】设君子莲雕塑的高度为米,证是等腰直角三角形,得米,再由锐角三角函数定义得,即可解决问题.
本题考查了解直角三角形的应用仰角俯角问题,熟练掌握仰角俯角定义和锐角三角函数定义是解题的关键.
20.【答案】解:设每包应该降价元,则每包的售价为元,每天可售出包,
依题意得:,
整理得:,
解得:,.
又要让顾客获得更大的优惠,
的值为.
答:每包应该降价元.
【解析】设每包应该降价元,则每包的售价为元,每天可售出包,根据每天该口罩的销售额为元,列出一元二次方程,解之即可得出的值,再结合要让顾客获得更大的优惠,即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
21.【答案】解:一次函数图象过点,
,解得,
点坐标为,
又反比例函数图象过点,
,
反比例函数解析式为;
联立一次函数和反比例函数表达式得:,
解得:,
即点.
【解析】用待定系数法即可求解;
联立一次函数和反比例函数表达式,即可求解.
本题主要考查函数图象的交点及待定系数法求函数解析式,掌握图象的交点的坐标满足两个函数解析式是解题的关键.
22.【答案】证明:四边形是平行四边形,
,
是边上的点,且不与重合,
,
∽.
解:是的中点,,
,
∽,
,
,
的长度是.
【解析】由平行四边形的性质得,即可根据“平行于三角形一边的直线和其它两边或两边的延长线相交所构成的三角形与原三角形相似”证明∽;
由是的中点,,得,由∽,得,则.
此题重点考查平行四边形的性质、相似三角形的判定与性质等知识,根据“平行于三角形一边的直线和其它两边或两边的延长线相交所构成的三角形与原三角形相似”证明∽是解题的关键.
23.【答案】
【解析】解:样本容量为,
则,对应的频数为,
,
故答案为:、;
第组人数所对应的扇形圆心角的度数为;
名,
答:估计这些学生中每天课前预习时不少于的学生有名.
先由第组频数及频率求出样本容量,再乘以第组频率可得的值,依据样本容量等于各组频数之和求出第组频数,继而可得的值;
用乘以第组频率可得答案;
总人数乘以第、组频数之和所占比例即可.
本题考查了条形统计图和扇形统计图的综合运用,掌握条形统计图能清楚地表示出每个项目的数据,扇形统计图直接反映部分占总体的百分比大小是关键.
24.【答案】解:把代入解析式得:,
解得;
设当时,与的函数表达式为,
把代入解析式得,,
当时,与的函数表达式为;
把代入得:;
把代入得:,
解得,
,
此次消毒有效.
【解析】先根据求出的值,再设当时,与的函数表达式为,把代入解析式求出即可;
分别把代入和求出,再相减与比较即可.
本题考查的是反比例函数与一次函数的综合应用、用待定系数法求反比例函数,掌握待定系数法求函数的解析式是解决此题的关键.
25.【答案】
【解析】解:当点运动到点时,两点停止运动,
,
,
运动时间的取值范围是,
故答案为:;
四边形是矩形,
,
在中,由勾股定理得,
,
可得:,
,
方程无解,
不存在的值,使得的长度等于.
存在秒,能够使得五边形的面积等于理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
,
解得:不合题意舍去,.
即当秒时,使得五边形的面积等于.
根据路程速度时间就可以表示出的取值范围;
根据勾股定理得出,解方程就可以得出答案;
根据五边形的面积等于建立方程,就可以求出的值.
本题属于四边形综合题,考查了行程问题的运用,一元二次方程的解法,二次函数的性质,勾股定理的运用,三角形面积公式的运用.在解答时要注意所求的解使实际问题有意义.
26.【答案】
【解析】解:,,
,
,
,
,
,
,
,
.
故答案为:,;
结论:是定值.
理由:如图中,
,
,
,
∽,
,
,
定值;
如图中,过点作于点设,
当,重合时,
,
,,,四点共圆,
,
,,
,
,
,
,,
,
,
,
;
如图中,当时,
,
,
,
,
,
.
综上所述,的值为或.
解直角三角形求出,,可得结论;
结论:是定值.证明∽,推出,由,可得定值;
如图中,过点作于点设,证明,,,四点共圆,推出,由,,推出,解直角三角形求出即可;如图中,当时,利用平行线分线段成比例定理求出即可.
本题属于几何变换综合题,考查了旋转变换,相似三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
第1页,共1页
2022-2023学年湖南省湘潭市湘潭子敬中学等三校九年级(下)开学数学试卷
学校:___________姓名:___________班级:___________考号:___________
得分
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
1. 用求根公式解一元二次方程时,,的值是( )
A. ,, B. ,,
C. ,, D. ,,
2. 某城市调查组为了解该城市的森林覆盖率,随机抽取面积为的土地进行调查后,估算出森林覆盖率为若该城市所占面积为,据此估算出该城市森林所占面积为( )
A. B. C. D.
3. 如图,若直线,且::,,则( )
A.
B.
C.
D.
4. 为了了解学校名学生周末完成作业所用时间,数学兴趣小组随机抽取了名学生进行了调查,在这个问题中,样本容量是( )
A. B. 被抽查的名学生 C. D. 名学生
5. 已知∽,且,,若的面积为,则的面积为( )
A. B. C. D. 无法计算
6. 如图,河堤横断面迎水坡的坡比是:,堤高,则坡面的长度是( )
A.
B.
C.
D.
7. 已知,则函数和的图象在同一平面直角坐标系中大致是( )
A. B.
C. D.
8. 读诗词,列方程:大江东去浪淘尽,千古风流人物;而立之年督东吴,早逝英年两位数,十位恰小个位三,个位平方与寿符诗词大意:周瑜英年早逝,逝世时的年龄是一个两位数,十位数字比个位数字小,个位数字的平方刚好是周瑜逝世时的年龄,设周瑜逝世时的年龄的个位数字为,则列出的方程正确的是( )
A. B.
C. D.
9. 对于反比例函数,下列说法正确的是( )
A. 它的图象分布在第一、三象限 B. 它的图象分布在第二、四象限
C. 点在函数图象上 D. 当时,的值随的增大而增大
10. 如图,在直角三角形中,,,则下列结论正确的是( )
A.
B.
C.
D. 若,则
11. 若关于的方程有两个相等的实数解,则的值可能为( )
A. B. C. D.
12. 如图,是边上一点,添加一个条件后,仍不能使∽的是( )
A.
B.
C.
D.
13. 若,则 .
14. 如图,点在函数的图象上,过点作轴于点,则的面积为______.
15. 甲、乙、丙、丁四个小组参加体育测试,他们成绩的平均分均为分,方差分别为:,,,,则这四个小组体育测试成绩最稳定的是______ 组
16. 请写出一个满足下列条件的一元二次方程:二次项系数为,且两根之和为正数,两根之积为负数你所写的一元二次方程是______ .
17. 计算:.
18. 如图,三个顶点的坐标分别为,,,以原点为位似中心,将放大为原来的倍得到.
在图中第一象限内画出符合要求的不要求写画法;
分别写出、、的坐标.
19. 为实现核心素养导向的教学目标,走向综合性、实践性的课程教学变革湘潭某中学推进项目式学习,组织九年级数学兴趣小组,测量莲城湘潭市的地标:君子莲雕塑君子莲雕塑采用抽象艺术手法,一朵含苞欲放的莲花,象征着美好的未来雕塑所蕴含的“出污泥而不染,濯清涟而不妖”的高洁品格,启发、激励着一代又一代的湘潭人民向着美好未来奋勇前行如图,测量小组在君子莲雕塑前的点观测雕塑顶部的仰角为,然后将观测点沿雕塑底部的水平方向移动了到点,在点观测的仰角为,求君子莲雕塑的高度结果保留一位小数,
20. 由于新冠疫情的影响,口罩需求量急剧上升,但在有关部门大力调控下,口罩价格没有上涨经调查发现,某社区药店把口罩定价为每包元时,一天可以卖出包,每降价元,可以多卖出包如果该药店想一天获得元口罩销售额,并且尽可能让顾客获得更大的优惠,应该降价多少元?
21. 如图,一次函数的图象与反比例函数为常数,且的图象交于、两点.
求反比例函数的表达式;
求点的坐标.
22. 如图,在 中,是边上的任意点不与重合,连接交于点.
求证:∽;
若是的中点,且,求的长度.
23. “双减”政策实施以来,越来越重视课堂效率了,比如有效的预习可以大幅度提高课堂效率八年级班数学学习兴趣小组为了了解全校八年级学生的预习情况,对该校八年级学生每天的课前预习时间进行了抽样调查,并将得到的数据分成组,下面是未完成的频数、频率分布表和扇形图.
组别 课前预习时间 频数人数 频率
请根据图表中的信息,回答下列问题:
表中的 ______ , ______ ;
试计算第组人数所对应的扇形圆心角的度数;
该校八年级有名学生,请估计这些学生中每天课前预习时不少于的学生人数.
24. 近期,流感进入发病高峰期,某校为预防流感,对教室进行熏药消毒,测得药物燃烧后室内每立方米空气中的含药量与时间之间的函数关系如图所示,已知药物燃烧时,满足;药物燃烧后,与成反比例,现测得药物分钟燃毕,此时室内每立方米空气中的含药量为请根据图中所提供的信息,解决下列问题:
求的值,并求当时,与的函数表达式;
研究表明,当空气中每立方米的含药量不低于毫克且持续时间不低于分钟时,才能有效杀灭空气中的病菌,则此次消毒是否有效?请计算说明.
25. 在矩形中,,,点从点开始沿边向终点以的速度移动,与此同时,点从点开始沿向终点以的速度移动,如果,分别从,同时出发,当点运动到点时,两点停止运动设运动时间为秒.
填空:运动时间的取值范围足______ .
是否存在的值,使得的长度等于?若存在,请求出此时的值,若不存在,请说明理由.
是否存在的值,使得五边形的面积等于?若存在,请求出此时的值,若不存在,请说明理由.
26. 如图,在中,,,,点是的中点,过点作交与点.
填空: ______ , ______ .
如图,将绕点顺时针旋转,连接、,交于点,、所在直线交于点,则:
试判断,在旋转过程中,是否为定值,并给出理由;
当为直角三角形时,求的长度.
答案和解析
1.【答案】
【解析】解:,
,
,,,
故选:.
先将方程化为一般形式,然后即可写出、、,本题得以解决.
本题考查解一元二次方程的一般形式、解一元二次方程公式法,解答本题的关键是明确一元二次方程的一般形式.
2.【答案】
【解析】解:由样本可知:该城市森林覆盖率是,
该城市森林所占面积为:,
故选:.
用样本估计出该城市森林覆盖率,计算即可.
本题考查的是样本去估计总体,根据样本估计出该城市森林覆盖率是解题的关键.
3.【答案】
【解析】解:直线,且::,
,
,
,
故选:.
由平行线分线段成比例定理得,则,即可得出结论.
本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.熟练掌握平行线分线段成比例定理是解题的关键
4.【答案】
【解析】解:为了了解学校名学生周末完成作业所用时间,数学兴趣小组随机抽取了名学生进行了调查,在这个问题中,样本容量是.
故选:.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
本题主要考查样本容量的含义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
5.【答案】
【解析】解:∽,,,
:::,
面积的比为:,
的面积为,
的面积为,
故选:.
根据相似三角形的面积比等于相似比的平方计算,得到答案.
本题考查的是相似三角形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
6.【答案】
【解析】解:因为坡度:,
,
,
.
故选D.
根据坡度坡角定义即可求出结果.
本题考查解直角三角形的应用.
7.【答案】
【解析】解:,
函数的图象分布在第一、三象限,反比例的图象分布在第二、四象限.
故选:.
根据反比例函数,当时,图象分布在第二、四象限和一次函数图象与系数的关系进行判断;
本题考查了一次函数图象和反比例函数的图象:反比例函数为双曲线,当时,图象分布在第一、三象限;当时,图象分布在第二、四象限.
8.【答案】
【解析】解:周瑜逝世时的年龄的个位数字为,且十位数字比个位数字小,
周瑜逝世时的年龄的十位数字为.
根据题意得:.
故选:.
由周瑜逝世时的年龄的十位数字与个位数字间的关系,可得出周瑜逝世时的年龄的十位数字为,结合周瑜逝世时的年龄的个位数字的平方刚好是周瑜逝世时的年龄,即可得出关于的一元二次方程,此题得解.
本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
9.【答案】
【解析】解:反比例函数,
,该函数的图象分布在第一、三象限,故选项A符合题意,选项B不符合题意;
当时,,故点在函数图象上,故选项C符合题意;
当时,随的增大而减小,故选项D不符合题意.
故选:.
根据反比例函数的解析式和反比例函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
本题考查反比例函数的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.
10.【答案】
【解析】解:由于,设,则,由勾股定理得,
,
,选项A不符合题意;
,选项B符合题意;
,选项C符合题意;
若,即,则,因此选项D符合题意.
故选:.
根据锐角三角函数的定义以及勾股定理逐项进行判断即可.
本题考查同角三角函数的关系,掌握锐角三角函数的定义以及勾股定理是正确解答的前提.
11.【答案】
【解析】解:由题意可知:,
,
故选:.
根据根的判别式即可求出答案.
本题考查了一元二次方程的根的判别式:当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根.
12.【答案】
【解析】解:、当时,再由,可得出∽,故此选项不合题意;
B、当时,再由,可得出∽,故此选项不合题意;
C、当时,无法得出∽,故此选项符合题意;
D、当时,即,再由,可得出∽,故此选项不合题意;
故选:.
直接利用相似三角形的判定方法分别分析得出答案.
此题主要考查了相似三角形的判定,正确掌握相似三角形的判定方法是解题关键.
13.【答案】
【解析】解:,根据等式的性质,得,
则,
故答案为:.
根据题意,即可得出答案.
本题考查等式的性质,属于基础题.
14.【答案】
【解析】解:由的几何意义可知:的面积为,
当时,
的面积为:
故答案为:
根据反比例函数的几何意义可知:的面积为,代入的值即可求出答案.
本题考查反比例函数系数的几何意义,解题的关键是根据三角形的面积为求解,本题属于基础题型.
15.【答案】甲
【解析】解:,,,,
,
这四个小组体育测试成绩最稳定的是甲组,
故答案为:甲.
根据方差的意义即可得出答案.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则与平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
16.【答案】答案不唯一
【解析】解:二次项系数为,且两根之和为正数,两根之积为负数.
这样的方程为.
故答案为:答案不唯一.
根据两根之和等于一次项系数除以二次项系数的相反数,两根之积等于常数项除二次项系数,直接写出一个方程即可,答案不唯一.
本题考查了一元二次方程根与系数的关系,熟记两根之和与两根之积是解题的关键.
17.【答案】解:原式
.
【解析】分别根据绝对值的性质,零指数幂及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行解答即可.
本题考查的是实数的运算,熟知绝对值的性质,零指数幂的运算法则,特殊角的三角函数值是解题的关键.
18.【答案】解:如图,为所作;,,.
【解析】利用关于以原点为位似中心的对应点的坐标特征写出点、、的坐标,然后描点即可.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形对应点的坐标的比等于或.
19.【答案】解:设君子莲雕塑的高度为米,
在中,,,
是等腰直角三角形,
米,
在中,米,,
,
,
解得:,
经检验,是原方程的解,且符合题意,
答:君子莲雕塑的高度约为米.
【解析】设君子莲雕塑的高度为米,证是等腰直角三角形,得米,再由锐角三角函数定义得,即可解决问题.
本题考查了解直角三角形的应用仰角俯角问题,熟练掌握仰角俯角定义和锐角三角函数定义是解题的关键.
20.【答案】解:设每包应该降价元,则每包的售价为元,每天可售出包,
依题意得:,
整理得:,
解得:,.
又要让顾客获得更大的优惠,
的值为.
答:每包应该降价元.
【解析】设每包应该降价元,则每包的售价为元,每天可售出包,根据每天该口罩的销售额为元,列出一元二次方程,解之即可得出的值,再结合要让顾客获得更大的优惠,即可得出结论.
本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
21.【答案】解:一次函数图象过点,
,解得,
点坐标为,
又反比例函数图象过点,
,
反比例函数解析式为;
联立一次函数和反比例函数表达式得:,
解得:,
即点.
【解析】用待定系数法即可求解;
联立一次函数和反比例函数表达式,即可求解.
本题主要考查函数图象的交点及待定系数法求函数解析式,掌握图象的交点的坐标满足两个函数解析式是解题的关键.
22.【答案】证明:四边形是平行四边形,
,
是边上的点,且不与重合,
,
∽.
解:是的中点,,
,
∽,
,
,
的长度是.
【解析】由平行四边形的性质得,即可根据“平行于三角形一边的直线和其它两边或两边的延长线相交所构成的三角形与原三角形相似”证明∽;
由是的中点,,得,由∽,得,则.
此题重点考查平行四边形的性质、相似三角形的判定与性质等知识,根据“平行于三角形一边的直线和其它两边或两边的延长线相交所构成的三角形与原三角形相似”证明∽是解题的关键.
23.【答案】
【解析】解:样本容量为,
则,对应的频数为,
,
故答案为:、;
第组人数所对应的扇形圆心角的度数为;
名,
答:估计这些学生中每天课前预习时不少于的学生有名.
先由第组频数及频率求出样本容量,再乘以第组频率可得的值,依据样本容量等于各组频数之和求出第组频数,继而可得的值;
用乘以第组频率可得答案;
总人数乘以第、组频数之和所占比例即可.
本题考查了条形统计图和扇形统计图的综合运用,掌握条形统计图能清楚地表示出每个项目的数据,扇形统计图直接反映部分占总体的百分比大小是关键.
24.【答案】解:把代入解析式得:,
解得;
设当时,与的函数表达式为,
把代入解析式得,,
当时,与的函数表达式为;
把代入得:;
把代入得:,
解得,
,
此次消毒有效.
【解析】先根据求出的值,再设当时,与的函数表达式为,把代入解析式求出即可;
分别把代入和求出,再相减与比较即可.
本题考查的是反比例函数与一次函数的综合应用、用待定系数法求反比例函数,掌握待定系数法求函数的解析式是解决此题的关键.
25.【答案】
【解析】解:当点运动到点时,两点停止运动,
,
,
运动时间的取值范围是,
故答案为:;
四边形是矩形,
,
在中,由勾股定理得,
,
可得:,
,
方程无解,
不存在的值,使得的长度等于.
存在秒,能够使得五边形的面积等于理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
,
解得:不合题意舍去,.
即当秒时,使得五边形的面积等于.
根据路程速度时间就可以表示出的取值范围;
根据勾股定理得出,解方程就可以得出答案;
根据五边形的面积等于建立方程,就可以求出的值.
本题属于四边形综合题,考查了行程问题的运用,一元二次方程的解法,二次函数的性质,勾股定理的运用,三角形面积公式的运用.在解答时要注意所求的解使实际问题有意义.
26.【答案】
【解析】解:,,
,
,
,
,
,
,
,
.
故答案为:,;
结论:是定值.
理由:如图中,
,
,
,
∽,
,
,
定值;
如图中,过点作于点设,
当,重合时,
,
,,,四点共圆,
,
,,
,
,
,
,,
,
,
,
;
如图中,当时,
,
,
,
,
,
.
综上所述,的值为或.
解直角三角形求出,,可得结论;
结论:是定值.证明∽,推出,由,可得定值;
如图中,过点作于点设,证明,,,四点共圆,推出,由,,推出,解直角三角形求出即可;如图中,当时,利用平行线分线段成比例定理求出即可.
本题属于几何变换综合题,考查了旋转变换,相似三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
第1页,共1页
同课章节目录
