北师大版八年级数学下册4.1因式分解导学案(含答案)
文档属性
| 名称 | 北师大版八年级数学下册4.1因式分解导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 582.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览

文档简介
4.1因式分解
导学案
学习目标
1.经历从分解因数到分解因式的类比过程.
2.了解因式分解的意义,以及它与整式乘法的相互关系.
3.感受因式分解在解决相关问题中的作用.
一、自学释疑
1.2×3×5等于多少?这是什么运算?
2.30=2×3×5是什么运算?
3. 2×3×5=30与30=2×3×5的运算是什么关系?
4.将一个多项式化成几个整式的积的形式,是用什么办法检验结果是否正确的?
二、合作探究
探究点一:
问题1:99 -99能被100整除吗?你是怎么想的?与同伴交流.还能被哪些正整数整除?
归纳:解决这个问题的关键在于把它化成几个数的积的形式.
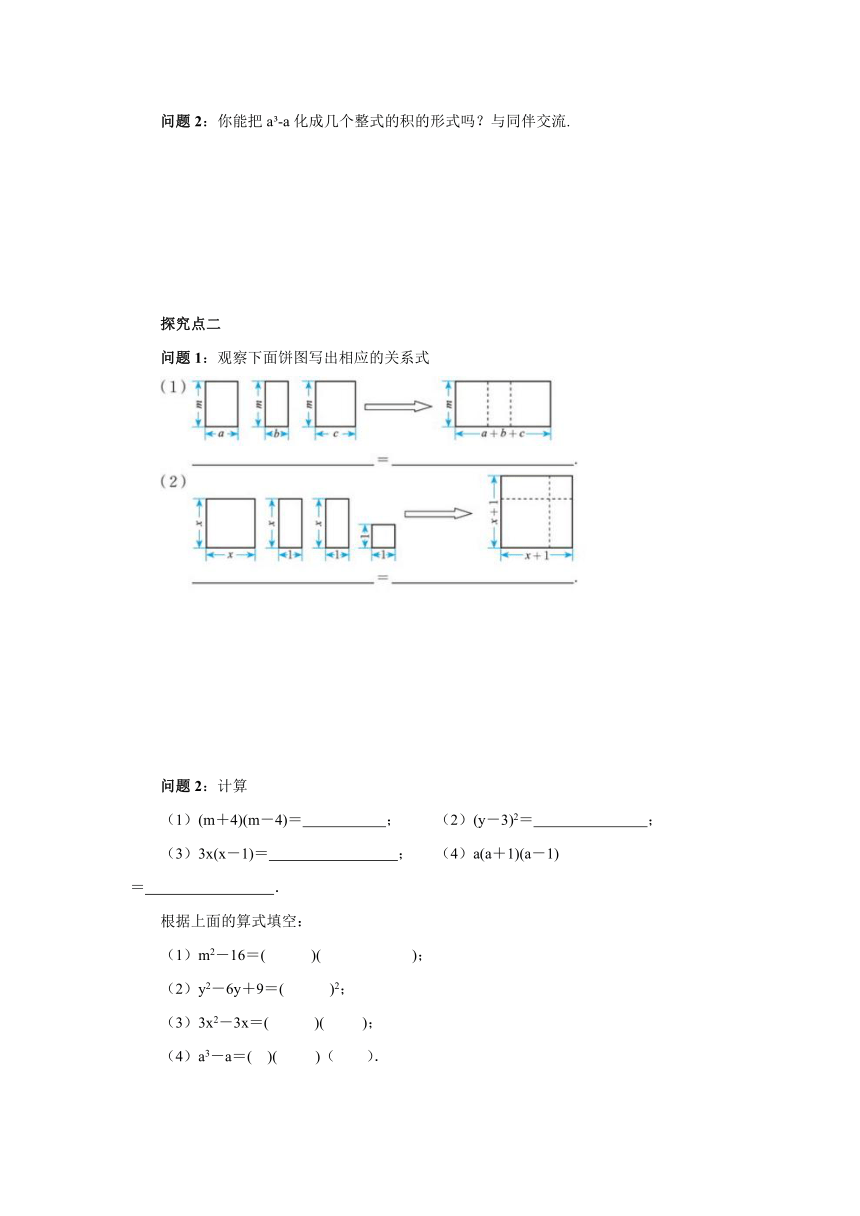
问题2:你能把a -a化成几个整式的积的形式吗?与同伴交流.
探究点二
问题1:观察下面饼图写出相应的关系式
问题2:计算
(1)(m+4)(m-4)= ; (2)(y-3)2= ;
(3)3x(x-1)= ; (4)a(a+1)(a-1)= .
根据上面的算式填空:
(1)m2-16=( )( );
(2)y2-6y+9=( )2;
(3)3x2-3x=( )( );
(4)a3-a=( )( )( ).
探究点三
问题1:因式分解:把一个 化成几个 的 的形式,这种变形叫做因式分解.因式分解也可称为 .
问题2:你能说明因式分解与整式的乘法有什么关系吗
多项式的因式分解与整式的乘法互为逆变形过程.因此可以用整式的乘法来检验分解因式是否正确.
探究点四
例1已知多项式x2-4x+m因式分解的结果为(x+a)(x-6),求2a-m的值.
解:由题意可知,x2-4x+m=(x+a)(x-6),
即x2-4x+m=x2+(a-6)x-6a.
所以解得
所以2a-m=2×2-(-12)=16.
强化训练
1.如图,将一个边长为m的正方形和一个宽为3的长方形纸片,拼出边长为(m+3)的正方形纸片,从这个过程中可得出的关系式为( )
A.m2+3(m+3)=(m+3)2 B.m2+3(m+6)=(m+3)2
C.m2+3(2m+3)=(m+3)2 D.m2+3(2m+6)=(m+3)2
2. 小马虎在一次因式分解练习中,一不小心弄脏了一部分,x2+x-6=(x+3)(x-■),你能帮他确定污染部分是多少吗?
随堂检测
1.下列各式从左到右的变形是分解因式的是( ).
A.a(a-b)=a -ab; B.a -2a+1=a(a-2)+1
C.x -x=x(x-1); D.x -=(x-)2
2.把下列各式分解因式正确的是( )
A.xy -x y=x(y -xy); B.9xyz-6 x y =3xyz(3-2xy)
C.3 a x-6bx+3x=3x(a -2b); D. x y + x y= xy(x+y)
3.(-2) +(-2) 等于( )
A.-2 B.-2 C.2 D.-2
4. 已知多项式 (a、b、c均为常数),分解因式的结果是(3x+1)(x-2) ,求a、b、c的值.
我的收获
.
参考答案
探究点一
问题1:解:99 -99 =98 ×99 ×100
=2×7×7×3×3×11×2×2×5×5
=2 ×3 ×5 ×7 ×11,
所以, 99 -99还能被2、3、4、5、6、7、8、9、10、11、12、14…整除:
解决这个问题的关键在于把它化成几个数的积的形式.
问题2:解:a -a
探究点二
解:(1)am+bm+cm=m(a+b+c)
(2)x +2x+1=(x+1)
=a(a -1)
=a(a+1)(a-1)
强化训练
1.C
2. 解:设污染部分为a,由整式乘法,得
(x+3)(x-a)
=x2+3x-ax-3a
=x2+(3-a)x-3a.
由题意可知,-3a=-6,
所以a=2.
随堂检测
1.C
2.D
3.C
4. 解:a=3,b=-5,c=-2.
导学案
学习目标
1.经历从分解因数到分解因式的类比过程.
2.了解因式分解的意义,以及它与整式乘法的相互关系.
3.感受因式分解在解决相关问题中的作用.
一、自学释疑
1.2×3×5等于多少?这是什么运算?
2.30=2×3×5是什么运算?
3. 2×3×5=30与30=2×3×5的运算是什么关系?
4.将一个多项式化成几个整式的积的形式,是用什么办法检验结果是否正确的?
二、合作探究
探究点一:
问题1:99 -99能被100整除吗?你是怎么想的?与同伴交流.还能被哪些正整数整除?
归纳:解决这个问题的关键在于把它化成几个数的积的形式.
问题2:你能把a -a化成几个整式的积的形式吗?与同伴交流.
探究点二
问题1:观察下面饼图写出相应的关系式
问题2:计算
(1)(m+4)(m-4)= ; (2)(y-3)2= ;
(3)3x(x-1)= ; (4)a(a+1)(a-1)= .
根据上面的算式填空:
(1)m2-16=( )( );
(2)y2-6y+9=( )2;
(3)3x2-3x=( )( );
(4)a3-a=( )( )( ).
探究点三
问题1:因式分解:把一个 化成几个 的 的形式,这种变形叫做因式分解.因式分解也可称为 .
问题2:你能说明因式分解与整式的乘法有什么关系吗
多项式的因式分解与整式的乘法互为逆变形过程.因此可以用整式的乘法来检验分解因式是否正确.
探究点四
例1已知多项式x2-4x+m因式分解的结果为(x+a)(x-6),求2a-m的值.
解:由题意可知,x2-4x+m=(x+a)(x-6),
即x2-4x+m=x2+(a-6)x-6a.
所以解得
所以2a-m=2×2-(-12)=16.
强化训练
1.如图,将一个边长为m的正方形和一个宽为3的长方形纸片,拼出边长为(m+3)的正方形纸片,从这个过程中可得出的关系式为( )
A.m2+3(m+3)=(m+3)2 B.m2+3(m+6)=(m+3)2
C.m2+3(2m+3)=(m+3)2 D.m2+3(2m+6)=(m+3)2
2. 小马虎在一次因式分解练习中,一不小心弄脏了一部分,x2+x-6=(x+3)(x-■),你能帮他确定污染部分是多少吗?
随堂检测
1.下列各式从左到右的变形是分解因式的是( ).
A.a(a-b)=a -ab; B.a -2a+1=a(a-2)+1
C.x -x=x(x-1); D.x -=(x-)2
2.把下列各式分解因式正确的是( )
A.xy -x y=x(y -xy); B.9xyz-6 x y =3xyz(3-2xy)
C.3 a x-6bx+3x=3x(a -2b); D. x y + x y= xy(x+y)
3.(-2) +(-2) 等于( )
A.-2 B.-2 C.2 D.-2
4. 已知多项式 (a、b、c均为常数),分解因式的结果是(3x+1)(x-2) ,求a、b、c的值.
我的收获
.
参考答案
探究点一
问题1:解:99 -99 =98 ×99 ×100
=2×7×7×3×3×11×2×2×5×5
=2 ×3 ×5 ×7 ×11,
所以, 99 -99还能被2、3、4、5、6、7、8、9、10、11、12、14…整除:
解决这个问题的关键在于把它化成几个数的积的形式.
问题2:解:a -a
探究点二
解:(1)am+bm+cm=m(a+b+c)
(2)x +2x+1=(x+1)
=a(a -1)
=a(a+1)(a-1)
强化训练
1.C
2. 解:设污染部分为a,由整式乘法,得
(x+3)(x-a)
=x2+3x-ax-3a
=x2+(3-a)x-3a.
由题意可知,-3a=-6,
所以a=2.
随堂检测
1.C
2.D
3.C
4. 解:a=3,b=-5,c=-2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
