有理数的乘方[上学期]

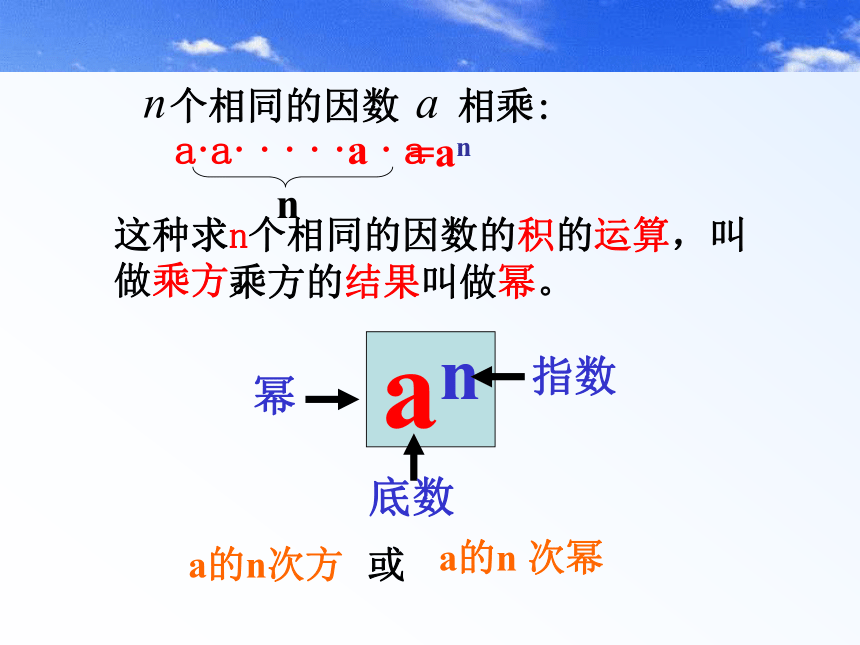
课件16张PPT。第二章 有理数有理数的乘方对折４次可得长方形　 个思考题：有一张白纸对折2次可得长方形　 个４对折３次可得长方形　 个８对折10次可得长方形　 个162×2×2×2×2×2×2×2×2×2对折100次可得长方形　 个(可用算式表示）10242×22×2×22×2×2×2=22=23=24=210=21002100个相同的因数 相乘:这种求n个相同的因数的积的运算，叫做乘方。=anan 指数底数幂a的n次方a的n 次幂或乘方的结果叫做幂。把下列乘方写成乘法的形式：
1、 = ；
2、 = ；
3、 = ；

把下列乘法的形式写成乘方的形式：
1、1×1×1×1×1×1×1= ；
2、3×3×3×3×3= ；
3、（－3）×（－3）×（－3）×（－3）= ；
4、 = ；
乘方的意义74535例2、说出下列式子分别表示什么意义？你能得出它们正确的结果吗？(－3)2　 －32　 (－2)3　－23例题解析例3计算:解:观察：如何确定有理数幂的符号？　　　　乘方的符号法则(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数.
(3)零的任何正整数次幂都是零;乘方运算的符号法则注意:　　有理数的乘方运算与有理数的加、减、乘、除一样，首先要确定幂的符号，然后再计算幂的绝对值．随堂练习口答：1、平方等于本身的数有_______。
2、平方得9的数是_______。平方是－9的数是______。例题解析例４分析：２００４是偶数，２００５是奇数例5
例六：判断下列各题是否正确：
（ ）① ；
（ ）② ；
（ ）③ ；
（ ）④
（ ）⑤ ； 对错错错( )4错1.当a是负数时，判断下列各式是否成立?
(1)a2=(-a)2； (2)a3=(-a)3；
(3)a2= ； (4)a3= .
2.平方得9的数有几个?是什么?
有没有平方得-9的有理数?为什么?
3.若(a+1)2+|b-2|=0，求a2000-b3的值? 拓展题乘方的故事　　有一个长工到一个财主家去做工，他和财主商定：“第一天给一分钱，第二天给两分钱，以后每天是前一天的平方.”财主答应了，到月底（30天）后，你猜一猜：财主会给长工多少钱？　　月底，长工兴冲冲的去领钱，他以为自己一下子可以领到一笔天文财富，结果财主只给了长工5分钱，而且还说是多给了他.　　长工算法：第一天1分，第二天2分，第三天4分，第四天16分，第五天256分……　　财主算法：第一天0.01元，第二天0.02元，第三天0.0004元，第四天0.00000016元……感悟与反思小结本节课你学到了什么?乘方的表示、底数、指数乘方的读法　　正数的任何次幂都是正数　　负数的奇次幂是负数，负数的偶次幂是正数　　0的正整数次幂都是0你相信吗？
把一张厚为0.1毫米的纸折叠27次后，它
的厚度相当于1.5个珠穆朗玛峰。问题解决 有一张厚度是0.1毫米的纸，将它对折1次，厚度为2×0.1毫米.(1)对折2次后，厚度为多少毫米？对折3次呢？4次呢？(2)对折27次后，厚度为多少米？227×0.1＝ 13421772.8 （毫米）（米）≈13422米解：依题意得：(3)珠穆朗玛峰高为8848.13米，这张纸对折27次后相当于1.5个珠穆朗玛峰那么高！