潍坊市2013-2014第二学期期中九年级数学试题(含答案)
文档属性
| 名称 | 潍坊市2013-2014第二学期期中九年级数学试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-09 11:20:19 | ||
图片预览

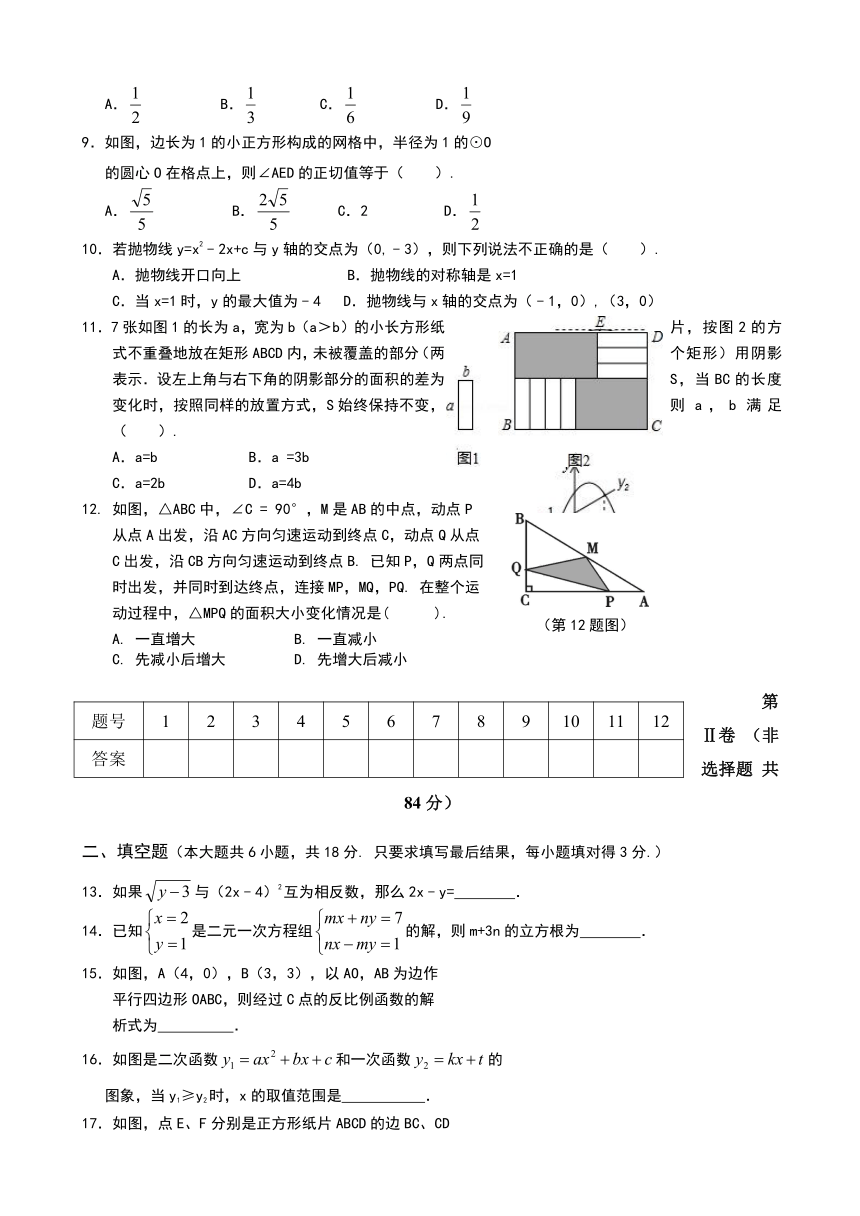

文档简介
2013—2014学年度第二学期期中质量检测
等级
九年级数学试题
(时间120分,满分120分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.答卷前,考生务必将自己的姓名、准考证号填写好.
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,共36分. ( http: / / www.21cnjy.com ) 在每小题给出的四个选项中,只有一个选项是正确的,请把正确的选项选出来,填在题后的表格里,每小题选对得3分. 错选、不选或多选均记零分.)
1.观察下列图形,既是轴对称图形又是中心对称图形的有( ).
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
据2014年1月24日某报道,某县2013年财政收入突破18亿元,在某省各县中排名
第二. 将18亿用科学记数法表示为( ).
A. 1.8×10 B. 1.8×109 C. 1.8×108 D. 1.8×1010
3.估计-1的值在( ).
A. 0到1之间 B. 1到2之间 C. 2到3之间 D. 3至4之间
4.下列运算正确的是( ).
A. B.(m2)3=m5 C.a2 a3=a5 D.(x+y)2=x2+y2
5.函数y=中自变量x的取值范围是( ).
A.x≥﹣3 B.x≥3 C.x≥0且x≠1 D.x≥﹣3且x≠1
已知⊙O1和⊙O2的半径分别是方程x2﹣4x+ 3=0的两根,且两圆的圆心距等于4,则
⊙O1与⊙O2的位置关系是( ).
A.外离 B.外切 C.相交 D.内切
7.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( ).
A.10π B.15π C.20π D.30π
暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综
合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( ).
A. B. C. D.
9.如图,边长为1的小正方形构成的网格中,半径为1的⊙O
的圆心O在格点上,则∠AED的正切值等于( ).
A. B. C.2 D.
10.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( ).
A.抛物线开口向上 B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4 D.抛物线与x轴的交点为(﹣1,0),(3,0)
11.7张如图1的长为a,宽为b(a>b) ( http: / / www.21cnjy.com )的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( ).
A.a=b B.a =3b
C.a=2b D.a=4b
12. 如图,△ABC中,∠C = 90°,M是AB的中点,动点P
从点A出发,沿AC方向匀速运动到终点C,动点Q从点
C出发,沿CB方向匀速运动到终点B. 已知P,Q两点同
时出发,并同时到达终点,连接MP,MQ,PQ. 在整个运
动过程中,△MPQ的面积大小变化情况是( ).
A. 一直增大 B. 一直减小
C. 先减小后增大 D. 先增大后减小
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,共18分. 只要求填写最后结果,每小题填对得3分.)
13.如果与(2x﹣4)2互为相反数,那么2x﹣y= .
14.已知是二元一次方程组的解,则m+3n的立方根为 .
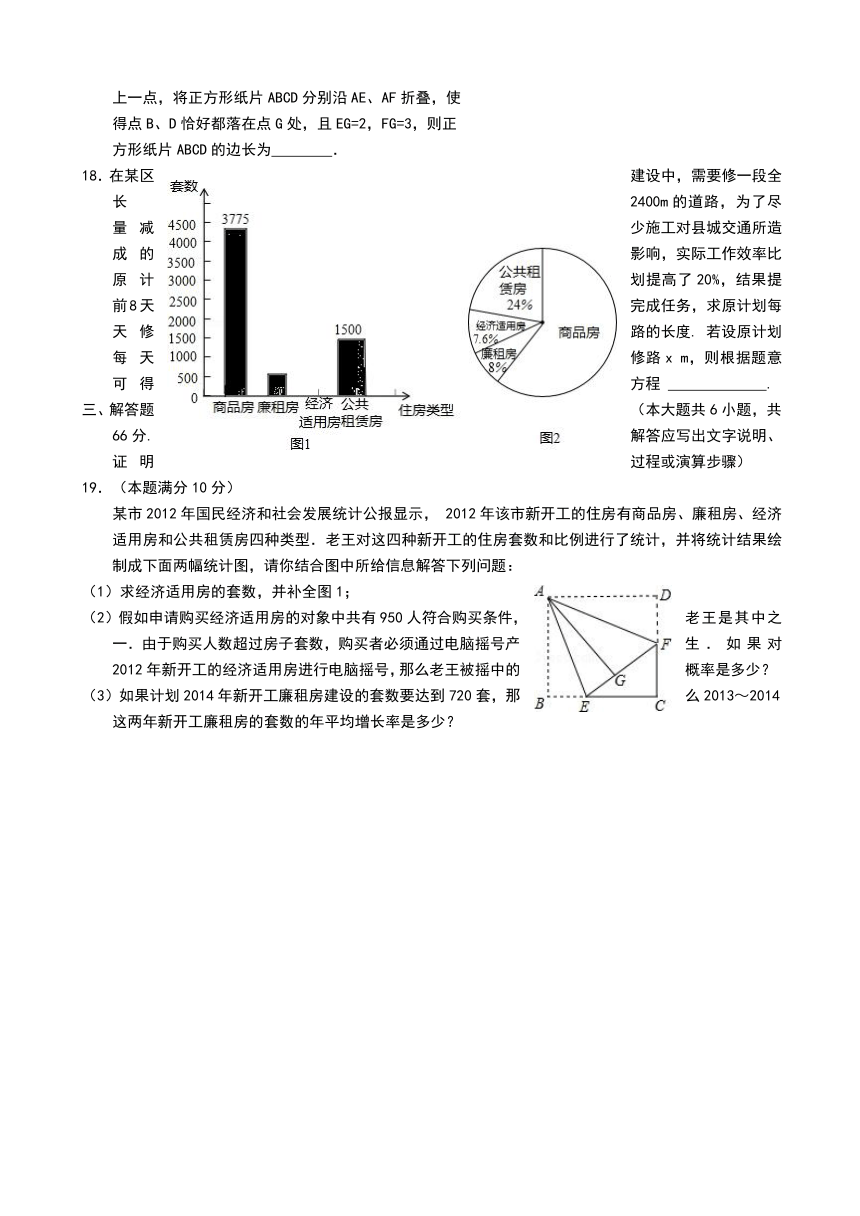
15.如图,A(4,0),B(3,3),以AO,AB为边作
平行四边形OABC,则经过C点的反比例函数的解
析式为 .
16.如图是二次函数和一次函数的
图象,当y1≥y2时,x的取值范围是 .
17.如图,点E、F分别是正方形纸片ABCD的边BC、CD
上一点,将正方形纸片ABCD分别沿AE、AF折叠,使
得点B、D恰好都落在点G处,且EG=2,FG=3,则正
方形纸片ABCD的边长为 .
18.在某区建设中,需要修一段全长2400 ( http: / / www.21cnjy.com )m的道路,为了尽量减少施工对县城交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8天完成任务,求原计划每天修路的长度. 若设原计划每天修路x m,则根据题意可得方程 .
三、解答题(本大题共6小题,共66分. 解答应写出文字说明、证明过程或演算步骤)
19.(本题满分10分)
某市2012年国民 ( http: / / www.21cnjy.com )经济和社会发展统计公报显示, 2012年该市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题:
(1)求经济适用房的套数,并补全图1;
(2)假如申请购买经济适用房的对象中共 ( http: / / www.21cnjy.com )有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2012年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果计划2014年新开工廉租房建设的套数要达到720套,那么2013~2014这两年新开工廉租房的套数的年平均增长率是多少?
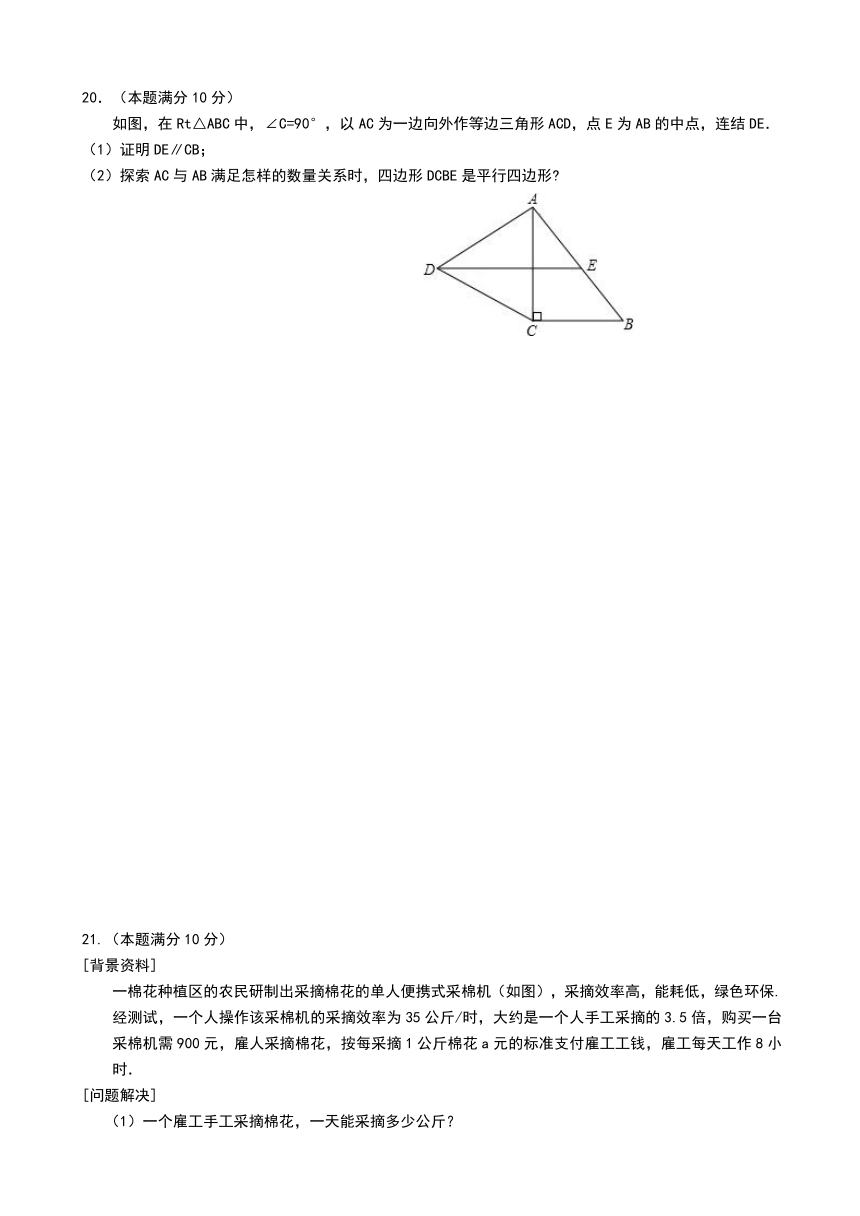
20.(本题满分10分)
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形
( http: / / www.21cnjy.com )
21.(本题满分10分)
[背景资料]
一棉花种植区的农民研制出采 ( http: / / www.21cnjy.com )摘棉花的单人便携式采棉机(如图),采摘效率高,能耗低,绿色环保. 经测试,一个人操作该采棉机的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,购买一台采棉机需900元,雇人采摘棉花,按每采摘1公斤棉花a元的标准支付雇工工钱,雇工每天工作8小时.
[问题解决]
(1)一个雇工手工采摘棉花,一天能采摘多少公斤?
(2)一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机,求a的值;
(3)在(2)的前提下,种植棉花的专业户张家和王家均雇人采摘棉花,王家雇佣的人数是张家的2倍,张家雇人手工采摘; 王家所雇的人中有的人自带采棉机采摘,的人手工采摘. 两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元,王家这次采摘棉花的总重量是多少?
22.(本题满分12分)
某校校园超市老板到批发中心 ( http: / / www.21cnjy.com )选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒的进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获 ( http: / / www.21cnjy.com )利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
( http: / / www.21cnjy.com )
23.(本题满分12分)
如图,⊙O的半径为 ( http: / / www.21cnjy.com )1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理
由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
24.(本题满分12分)
如图,四边形OA ( http: / / www.21cnjy.com )BC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t
为何值时,S的值最大;
是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,
说明理由.
2014年初三模拟考试数学试题参考答案及评分标准
一、C BBCD B B B DC BC
二、13.1 14.2 15. y=﹣ 16.﹣1≤x≤2 17.6 18.-= 8
三、19. 解:(1)1500÷24%=6250. …………………………………………1分
6250×7.6%=475,所以经济适用房的套数有475套; ……………2分
如图所示: …………………………………………4分
( http: / / www.21cnjy.com )
(2)老王被摇中的概率为:; ………………………………7分
(3)设2013~2014这两年新开工廉租房的套数的年平均增长率为x,
因为2012年廉租房共有6250×8%=500(套) …………………………8分
所以依题意,得 500(1+x)2=720 ……………………………9分
解这个方程得,x1=0.2,x2=﹣2.2(不合题意,舍去)
答:这两年新开工廉租房的套数的年平均增长率为20%. …………………10分
20. (1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE==AE. ……… ……………1分
∵△ACD是等边三角形,∴AD=CD.………2分
在△ADE与△CDE中,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.……………4分
∵∠DCB=150°,∴∠EDC+∠DCB=180°.∴DE∥CB. …………………………5分
备注:还可利用三线合一证明.
(2)解:∵∠DCB=150°,若四边 ( http: / / www.21cnjy.com )形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.∴∠B=30°. ………………………………………………7分
在Rt△ACB中,sinB=,sin30°=,AC=或AB=2AC.……9分
∴当AC=或AB=2AC时,四边形DCBE是平行四边形. ……………10分
21. 解:(1)∵一个人操作该采棉机 ( http: / / www.21cnjy.com )的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,∴一个人手工采摘棉花的效率为:35÷3.5=10(公斤/时),
∵雇工每天工作8小时,∴一个雇工手工一天能采摘棉花10×8=80(公斤). …3分
(2)由题意,得80×7.5a=900,解得a=. ……………………………………6分
(3)设张家雇佣x人采摘棉花,则王家雇佣2x人采摘棉花,
其中王家所雇的人中有的人自带彩棉机采摘,的人手工采摘.
∵张家雇佣的x人全部手工采摘棉花,且采摘完毕后,张家付给雇工工钱总额为14400元,∴采摘的天数为:=, ……………………………………………8分
∴王家这次采摘棉花的总重量是:
(35×8×+80×)×=51200(公斤). …………………………………10分
22. 解:(1)设y与x之间的函数关系式为y=kx+b,由函数图象,得
, ……………………………………………………………………1分
解得:,∴y与x之间的函数关系式为y=﹣x+300; ………………………3分
(2)∵y=﹣x+300;∴当x=120时,y=180. ……………………………………………4分
设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得
120a+180×2a=7200, …………………………………………………………………6分
解得:a=15,∴乙品牌的进货单价是30元.
答:甲、乙两种品牌的文具盒进货单价分别为15元,30元. ……………………7分
(3)设甲品牌进货m个,则乙品牌的进货(﹣m+300)个,由题意,得
, ………………………………………………9分
解得:180≤m≤181,∵m为整数,∴m=180,181.
∴共有两种进货方案:
方案1:甲品牌进货180个,则乙品牌的进货120个;
方案2:甲品牌进货181个,则乙品牌的进货119个; ……………………10分
设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得
W=4m+9(﹣m+300)=﹣5m+2700.
∵k=﹣5<0,∴W随m的增大而减小,
∴m=180时,W最大=1800元. ……………………………………………………12分
23. (1)PN与⊙O相切. ………………………………………………………………1分
证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN. …………………………………………………2分
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°.即PN与⊙O相切. ……………………4分
(2)成立. ………………………………………………………………………………5分
证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,∴∠OMA+∠OAM=90°,∴∠PNM+∠ONA=90°.………………………7分
∴∠PNO=180°﹣90°=90°.即PN与⊙O相切. ………………………………8分
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°, ………………………9分
∵∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=ON sin60°=1×=. …… ………………10分
S阴影=S△AOC+S扇形AON﹣S△CON =OC OA+CO NE
=×1×1+π﹣×1× =+π﹣. ………………………………12分
( http: / / www.21cnjy.com )
24. 解:(1)点M………………………………………………………………………1分
(2)经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t,
∵OC=OA=4, ∠AOC=90°,∴∠OAC=45°.
∵CB∥OA, ∴∠BCA=∠MAQ=45°,
∵NP⊥OA, ∴∠CNQ=90°.
∴QN=CN=3﹣t,∴PQ=4-(3-t)=1+t…………………………………………………2分
∴S△AMQ=AM PQ=(4﹣2t)(1+t)=﹣t2+t+2.……………………………………3分
∴S=﹣t2+t+2=﹣t2+t﹣ + +2 =﹣(t﹣)2+,……………………………5分
∵0≤t≤2,∴当 时,S的值最大.………………………………6分
(3)存在.…………………………………………………………………7分
设经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t
①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高,∴PQ是底边MA的中线.
∴PQ=AP=MA.∴1+t=(4﹣2t),∴t=
∴OM=1,∴点M的坐标为(1,0) ……………10分
②若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA
∴1+t=4﹣2t, ∴t=1.
∴OM=2,∴点M的坐标为(2,0). ………12分
(第12题图)
等级
九年级数学试题
(时间120分,满分120分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.答卷前,考生务必将自己的姓名、准考证号填写好.
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,共36分. ( http: / / www.21cnjy.com ) 在每小题给出的四个选项中,只有一个选项是正确的,请把正确的选项选出来,填在题后的表格里,每小题选对得3分. 错选、不选或多选均记零分.)
1.观察下列图形,既是轴对称图形又是中心对称图形的有( ).
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
据2014年1月24日某报道,某县2013年财政收入突破18亿元,在某省各县中排名
第二. 将18亿用科学记数法表示为( ).
A. 1.8×10 B. 1.8×109 C. 1.8×108 D. 1.8×1010
3.估计-1的值在( ).
A. 0到1之间 B. 1到2之间 C. 2到3之间 D. 3至4之间
4.下列运算正确的是( ).
A. B.(m2)3=m5 C.a2 a3=a5 D.(x+y)2=x2+y2
5.函数y=中自变量x的取值范围是( ).
A.x≥﹣3 B.x≥3 C.x≥0且x≠1 D.x≥﹣3且x≠1
已知⊙O1和⊙O2的半径分别是方程x2﹣4x+ 3=0的两根,且两圆的圆心距等于4,则
⊙O1与⊙O2的位置关系是( ).
A.外离 B.外切 C.相交 D.内切
7.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( ).
A.10π B.15π C.20π D.30π
暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综
合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( ).
A. B. C. D.
9.如图,边长为1的小正方形构成的网格中,半径为1的⊙O
的圆心O在格点上,则∠AED的正切值等于( ).
A. B. C.2 D.
10.若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( ).
A.抛物线开口向上 B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4 D.抛物线与x轴的交点为(﹣1,0),(3,0)
11.7张如图1的长为a,宽为b(a>b) ( http: / / www.21cnjy.com )的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( ).
A.a=b B.a =3b
C.a=2b D.a=4b
12. 如图,△ABC中,∠C = 90°,M是AB的中点,动点P
从点A出发,沿AC方向匀速运动到终点C,动点Q从点
C出发,沿CB方向匀速运动到终点B. 已知P,Q两点同
时出发,并同时到达终点,连接MP,MQ,PQ. 在整个运
动过程中,△MPQ的面积大小变化情况是( ).
A. 一直增大 B. 一直减小
C. 先减小后增大 D. 先增大后减小
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,共18分. 只要求填写最后结果,每小题填对得3分.)
13.如果与(2x﹣4)2互为相反数,那么2x﹣y= .
14.已知是二元一次方程组的解,则m+3n的立方根为 .
15.如图,A(4,0),B(3,3),以AO,AB为边作
平行四边形OABC,则经过C点的反比例函数的解
析式为 .
16.如图是二次函数和一次函数的
图象,当y1≥y2时,x的取值范围是 .
17.如图,点E、F分别是正方形纸片ABCD的边BC、CD
上一点,将正方形纸片ABCD分别沿AE、AF折叠,使
得点B、D恰好都落在点G处,且EG=2,FG=3,则正
方形纸片ABCD的边长为 .
18.在某区建设中,需要修一段全长2400 ( http: / / www.21cnjy.com )m的道路,为了尽量减少施工对县城交通所造成的影响,实际工作效率比原计划提高了20%,结果提前8天完成任务,求原计划每天修路的长度. 若设原计划每天修路x m,则根据题意可得方程 .
三、解答题(本大题共6小题,共66分. 解答应写出文字说明、证明过程或演算步骤)
19.(本题满分10分)
某市2012年国民 ( http: / / www.21cnjy.com )经济和社会发展统计公报显示, 2012年该市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题:
(1)求经济适用房的套数,并补全图1;
(2)假如申请购买经济适用房的对象中共 ( http: / / www.21cnjy.com )有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2012年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果计划2014年新开工廉租房建设的套数要达到720套,那么2013~2014这两年新开工廉租房的套数的年平均增长率是多少?
20.(本题满分10分)
如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形
( http: / / www.21cnjy.com )
21.(本题满分10分)
[背景资料]
一棉花种植区的农民研制出采 ( http: / / www.21cnjy.com )摘棉花的单人便携式采棉机(如图),采摘效率高,能耗低,绿色环保. 经测试,一个人操作该采棉机的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,购买一台采棉机需900元,雇人采摘棉花,按每采摘1公斤棉花a元的标准支付雇工工钱,雇工每天工作8小时.
[问题解决]
(1)一个雇工手工采摘棉花,一天能采摘多少公斤?
(2)一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机,求a的值;
(3)在(2)的前提下,种植棉花的专业户张家和王家均雇人采摘棉花,王家雇佣的人数是张家的2倍,张家雇人手工采摘; 王家所雇的人中有的人自带采棉机采摘,的人手工采摘. 两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元,王家这次采摘棉花的总重量是多少?
22.(本题满分12分)
某校校园超市老板到批发中心 ( http: / / www.21cnjy.com )选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒的进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获 ( http: / / www.21cnjy.com )利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
( http: / / www.21cnjy.com )
23.(本题满分12分)
如图,⊙O的半径为 ( http: / / www.21cnjy.com )1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理
由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
( http: / / www.21cnjy.com )
24.(本题满分12分)
如图,四边形OA ( http: / / www.21cnjy.com )BC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t
为何值时,S的值最大;
是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,
说明理由.
2014年初三模拟考试数学试题参考答案及评分标准
一、C BBCD B B B DC BC
二、13.1 14.2 15. y=﹣ 16.﹣1≤x≤2 17.6 18.-= 8
三、19. 解:(1)1500÷24%=6250. …………………………………………1分
6250×7.6%=475,所以经济适用房的套数有475套; ……………2分
如图所示: …………………………………………4分
( http: / / www.21cnjy.com )
(2)老王被摇中的概率为:; ………………………………7分
(3)设2013~2014这两年新开工廉租房的套数的年平均增长率为x,
因为2012年廉租房共有6250×8%=500(套) …………………………8分
所以依题意,得 500(1+x)2=720 ……………………………9分
解这个方程得,x1=0.2,x2=﹣2.2(不合题意,舍去)
答:这两年新开工廉租房的套数的年平均增长率为20%. …………………10分
20. (1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE==AE. ……… ……………1分
∵△ACD是等边三角形,∴AD=CD.………2分
在△ADE与△CDE中,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.……………4分
∵∠DCB=150°,∴∠EDC+∠DCB=180°.∴DE∥CB. …………………………5分
备注:还可利用三线合一证明.
(2)解:∵∠DCB=150°,若四边 ( http: / / www.21cnjy.com )形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.∴∠B=30°. ………………………………………………7分
在Rt△ACB中,sinB=,sin30°=,AC=或AB=2AC.……9分
∴当AC=或AB=2AC时,四边形DCBE是平行四边形. ……………10分
21. 解:(1)∵一个人操作该采棉机 ( http: / / www.21cnjy.com )的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,∴一个人手工采摘棉花的效率为:35÷3.5=10(公斤/时),
∵雇工每天工作8小时,∴一个雇工手工一天能采摘棉花10×8=80(公斤). …3分
(2)由题意,得80×7.5a=900,解得a=. ……………………………………6分
(3)设张家雇佣x人采摘棉花,则王家雇佣2x人采摘棉花,
其中王家所雇的人中有的人自带彩棉机采摘,的人手工采摘.
∵张家雇佣的x人全部手工采摘棉花,且采摘完毕后,张家付给雇工工钱总额为14400元,∴采摘的天数为:=, ……………………………………………8分
∴王家这次采摘棉花的总重量是:
(35×8×+80×)×=51200(公斤). …………………………………10分
22. 解:(1)设y与x之间的函数关系式为y=kx+b,由函数图象,得
, ……………………………………………………………………1分
解得:,∴y与x之间的函数关系式为y=﹣x+300; ………………………3分
(2)∵y=﹣x+300;∴当x=120时,y=180. ……………………………………………4分
设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得
120a+180×2a=7200, …………………………………………………………………6分
解得:a=15,∴乙品牌的进货单价是30元.
答:甲、乙两种品牌的文具盒进货单价分别为15元,30元. ……………………7分
(3)设甲品牌进货m个,则乙品牌的进货(﹣m+300)个,由题意,得
, ………………………………………………9分
解得:180≤m≤181,∵m为整数,∴m=180,181.
∴共有两种进货方案:
方案1:甲品牌进货180个,则乙品牌的进货120个;
方案2:甲品牌进货181个,则乙品牌的进货119个; ……………………10分
设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得
W=4m+9(﹣m+300)=﹣5m+2700.
∵k=﹣5<0,∴W随m的增大而减小,
∴m=180时,W最大=1800元. ……………………………………………………12分
23. (1)PN与⊙O相切. ………………………………………………………………1分
证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN. …………………………………………………2分
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°.即PN与⊙O相切. ……………………4分
(2)成立. ………………………………………………………………………………5分
证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.
在Rt△AOM中,∴∠OMA+∠OAM=90°,∴∠PNM+∠ONA=90°.………………………7分
∴∠PNO=180°﹣90°=90°.即PN与⊙O相切. ………………………………8分
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°, ………………………9分
∵∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=ON sin60°=1×=. …… ………………10分
S阴影=S△AOC+S扇形AON﹣S△CON =OC OA+CO NE
=×1×1+π﹣×1× =+π﹣. ………………………………12分
( http: / / www.21cnjy.com )
24. 解:(1)点M………………………………………………………………………1分
(2)经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t,
∵OC=OA=4, ∠AOC=90°,∴∠OAC=45°.
∵CB∥OA, ∴∠BCA=∠MAQ=45°,
∵NP⊥OA, ∴∠CNQ=90°.
∴QN=CN=3﹣t,∴PQ=4-(3-t)=1+t…………………………………………………2分
∴S△AMQ=AM PQ=(4﹣2t)(1+t)=﹣t2+t+2.……………………………………3分
∴S=﹣t2+t+2=﹣t2+t﹣ + +2 =﹣(t﹣)2+,……………………………5分
∵0≤t≤2,∴当 时,S的值最大.………………………………6分
(3)存在.…………………………………………………………………7分
设经过t秒时,NB=t,OM=2t,则CN=3﹣t,AM=4﹣2t
①若∠AQM=90°,则PQ是等腰Rt△MQA底边MA上的高,∴PQ是底边MA的中线.
∴PQ=AP=MA.∴1+t=(4﹣2t),∴t=
∴OM=1,∴点M的坐标为(1,0) ……………10分
②若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA
∴1+t=4﹣2t, ∴t=1.
∴OM=2,∴点M的坐标为(2,0). ………12分
(第12题图)
同课章节目录
