人教版八年级下册 18.1.2平行四边形的判定基础练习 含答案
文档属性
| 名称 | 人教版八年级下册 18.1.2平行四边形的判定基础练习 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 410.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 15:06:58 | ||
图片预览



文档简介
18.1.2平行四边形的判定 基础练习
一、单选题
1.已知,,则四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.如图,A,B两地被池塘隔开,为了测出A,B两地间的距离,小明先在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=15米,由此他知道了A,B两地间的距离为( )
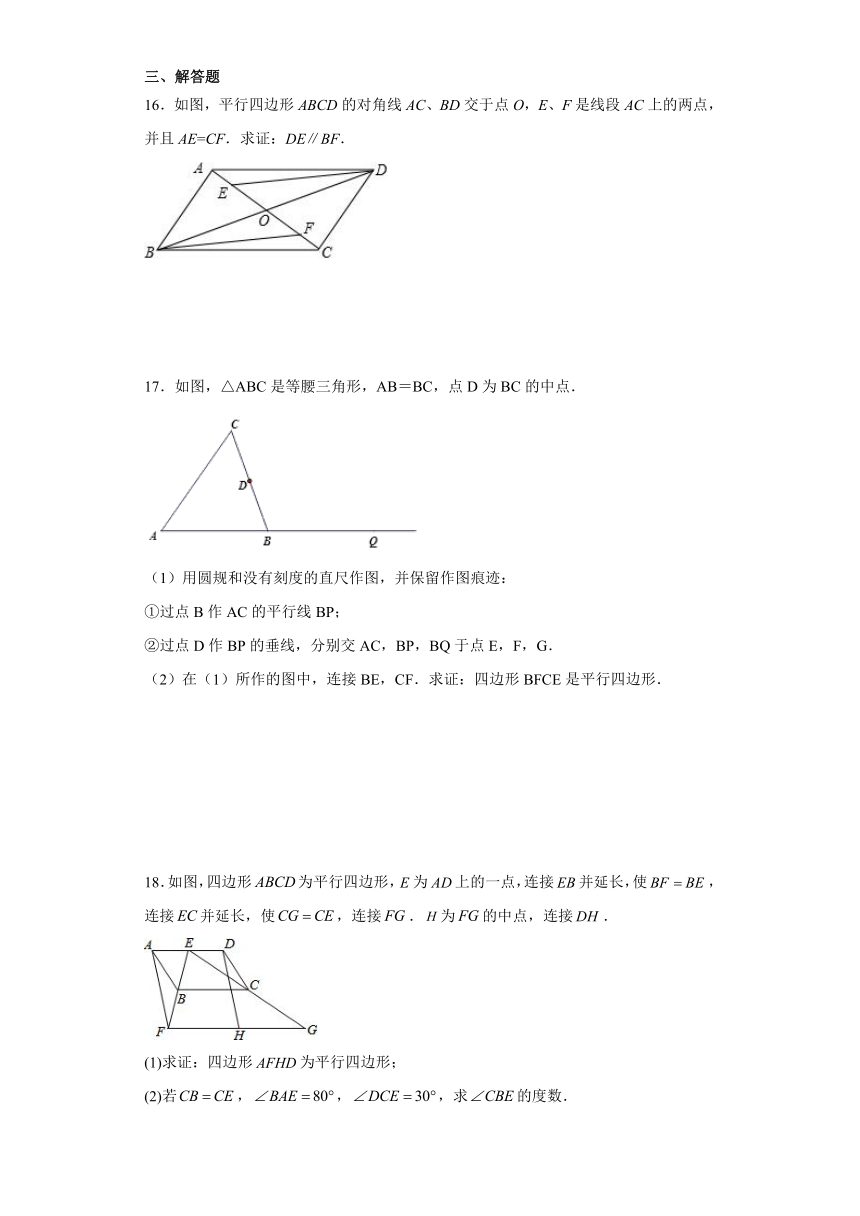
A.15米 B.20米 C.25米 D.30米
3.下列关于判定平行四边形的说法错误的是( )
A.一组对角相等且一组对边平行的四边形
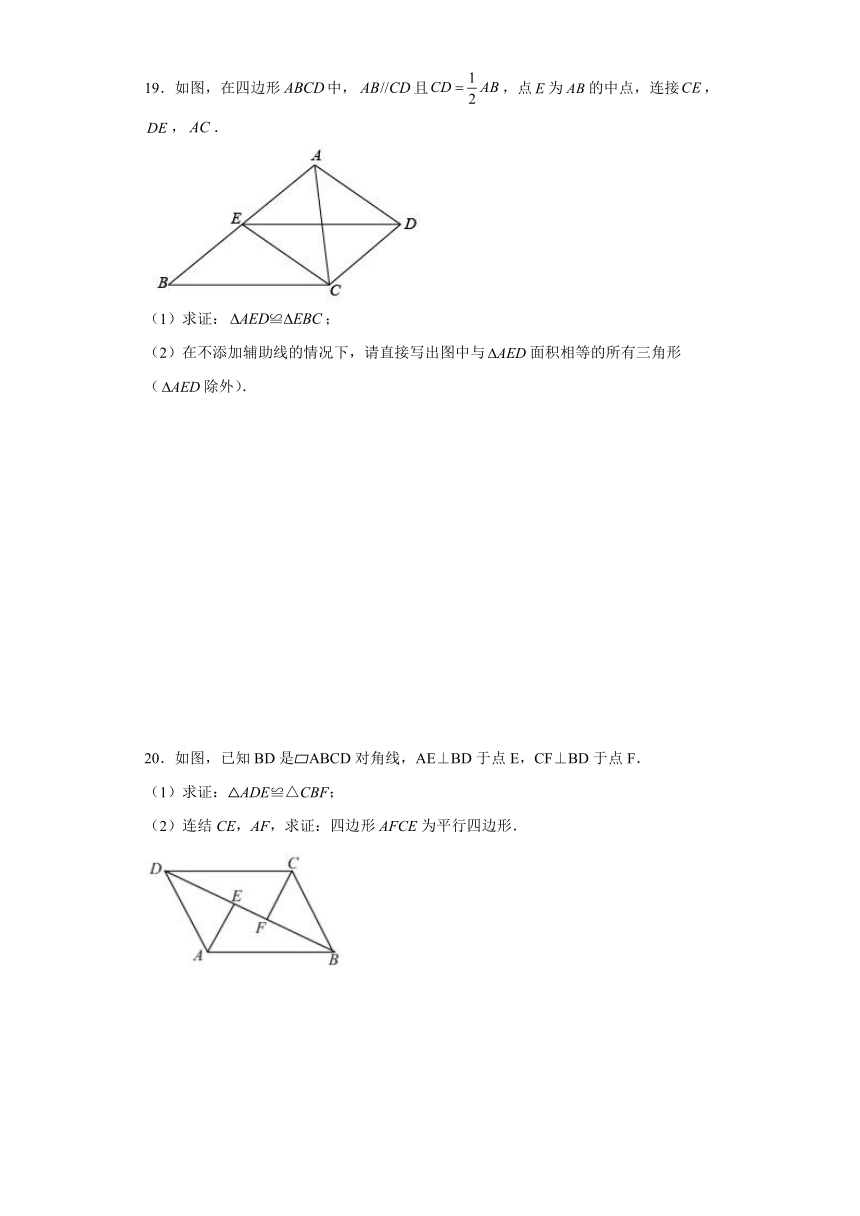
B.一组对边相等且另一组对边平行的四边形
C.两组对角分别相等的四边形
D.四条边相等的四边形
4.某数学小组发现可将如图所示的四个相同的直角三角形拼接成一个四边形(无重叠、无缝隙),则可拼接成不同的平行四边形的方法共有( )
A.种 B.种 C.种 D.种
5.如图,A,B为定点,定直线,P是l上一动点,点M,N分别为的中点.下列各值:①线段的长;②的周长;③的面积;④直线之间的距离;⑤的大小.其中会随着点P的移动发生变化的值是( )
A.②③ B.①③④ C.④⑤ D.②⑤
6.如图所示,四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( )
A.23° B.41° C.46° D.47°
7.下列各组条件中,不能判断一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形 B.两组对角分别相等的四边形
C.一组对边平行另一组对边相等的四边形 D.两条对角线互相平分的四边形
8.如图,现有一把直尺和一块三角尺,其中,,.点对应直尺的刻度为12,将该三角尺沿着直尺边缘平移,使得移动到,点对应直尺的刻度为0,则四边形的面积是( ).
A.96 B. C.192 D.
9.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=;④S△AEF=.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,四边形中,于点,,,,点是的中点,连接,则的最大值是( )
A. B. C. D.
二、填空题
11.如图,AB是池塘两端,设计一方法测量AB的距离,取点C,连接AC、BC,再取它们的中点D、E,测得DE=10米,则AB=_____米.
12.小明做了一个平行四边形的纸板,但他不确定纸板形状是否标准,小聪用刻度尺量了这个四边形的四条边长,然后说这个纸板是标准的平行四边形,小聪的依据是_____.
13.如图,在中,,E,F分别是,上两点,,,点P,Q,D分别是,,的中点,则_________.
14.如图,在 ABCD中,与相交于点,是边的中点,,则的长是______.
15.如图,在△ABC中,AB=AC=6,中线CE=5.延长AB到点D,使BD=AB,则CD的长_____________.
三、解答题
16.如图,平行四边形ABCD的对角线AC、BD交于点O,E、F是线段AC上的两点,并且AE=CF.求证:DE∥BF.
17.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
18.如图,四边形为平行四边形,为上的一点,连接并延长,使,连接并延长,使,连接.为的中点,连接.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
19.如图,在四边形中,且,点为的中点,连接,,.
(1)求证:;
(2)在不添加辅助线的情况下,请直接写出图中与面积相等的所有三角形(除外).
20.如图,已知BD是 ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ADE≌△CBF;
(2)连结CE,AF,求证:四边形AFCE为平行四边形.
参考答案
1.A
2.D
3.B
4.C
5.D
6.A
7.C
8.B
9.C
10.A
11.20
12.两组对边分别相等的四边形是平行四边形.
13.5
14.2
15.10
16.如图,连接BE,DF.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴DE∥BF.
17.(1)①作∠CBQ的平分线BP;②过点D作BP的垂线;
(2)∵BP//CE,∴∠ECD=∠FBD,∠CED=∠BFD,∵点D是BC的中点,∴CD=BD,∴△CDE≌△BDF,∴CE=BF,∵BF//CE,BF=CE,∴四边形BFCE是平行四边形.
18.(1)解:证明:四边形是平行四边形,
,,
,,
是的中位线,
,,
为的中点,
,
,,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
,
,
,
,
.
19.(1)∵点为的中点
∴
∵
∴CD=AE
∵
∴四边形ADCE是平行四边形
∴,AD∥CE
∴
∵,,,
∴(SAS)
(2)∵
∴与面积相等;
∵∵点为的中点
∴
∵与高相等
∴与面积相等;
∵
∴CD=AE,CD=EB
∵与高相等
∴与面积相等;
∵与高相等
∴与面积相等;
∴与面积相等的三角形有:、、、.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥AD,
∴∠EAD=90°,同理∠BCF=90°.
∴∠EAD=∠BCF.
在△AED和△CFB中
∠ADB=∠CBD,AD=BC,∠EAD=∠BCF,
∴△ADE≌△CBF.
(2)结论:四边形AECF是平行四边形.
理由:连接AC,
∵四边形ABCD是平行四边形,
∴AC平分BD,
由(1)△ADE≌△CBF,
∴AE=CF,∠AED=∠BFC,
∴AE∥CF,
∴四边形AECF是平行四边形.
一、单选题
1.已知,,则四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2.如图,A,B两地被池塘隔开,为了测出A,B两地间的距离,小明先在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=15米,由此他知道了A,B两地间的距离为( )
A.15米 B.20米 C.25米 D.30米
3.下列关于判定平行四边形的说法错误的是( )
A.一组对角相等且一组对边平行的四边形
B.一组对边相等且另一组对边平行的四边形
C.两组对角分别相等的四边形
D.四条边相等的四边形
4.某数学小组发现可将如图所示的四个相同的直角三角形拼接成一个四边形(无重叠、无缝隙),则可拼接成不同的平行四边形的方法共有( )
A.种 B.种 C.种 D.种
5.如图,A,B为定点,定直线,P是l上一动点,点M,N分别为的中点.下列各值:①线段的长;②的周长;③的面积;④直线之间的距离;⑤的大小.其中会随着点P的移动发生变化的值是( )
A.②③ B.①③④ C.④⑤ D.②⑤
6.如图所示,四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( )
A.23° B.41° C.46° D.47°
7.下列各组条件中,不能判断一个四边形是平行四边形的是( )
A.两组对边分别平行的四边形 B.两组对角分别相等的四边形
C.一组对边平行另一组对边相等的四边形 D.两条对角线互相平分的四边形
8.如图,现有一把直尺和一块三角尺,其中,,.点对应直尺的刻度为12,将该三角尺沿着直尺边缘平移,使得移动到,点对应直尺的刻度为0,则四边形的面积是( ).
A.96 B. C.192 D.
9.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=;④S△AEF=.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,四边形中,于点,,,,点是的中点,连接,则的最大值是( )
A. B. C. D.
二、填空题
11.如图,AB是池塘两端,设计一方法测量AB的距离,取点C,连接AC、BC,再取它们的中点D、E,测得DE=10米,则AB=_____米.
12.小明做了一个平行四边形的纸板,但他不确定纸板形状是否标准,小聪用刻度尺量了这个四边形的四条边长,然后说这个纸板是标准的平行四边形,小聪的依据是_____.
13.如图,在中,,E,F分别是,上两点,,,点P,Q,D分别是,,的中点,则_________.
14.如图,在 ABCD中,与相交于点,是边的中点,,则的长是______.
15.如图,在△ABC中,AB=AC=6,中线CE=5.延长AB到点D,使BD=AB,则CD的长_____________.
三、解答题
16.如图,平行四边形ABCD的对角线AC、BD交于点O,E、F是线段AC上的两点,并且AE=CF.求证:DE∥BF.
17.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
18.如图,四边形为平行四边形,为上的一点,连接并延长,使,连接并延长,使,连接.为的中点,连接.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
19.如图,在四边形中,且,点为的中点,连接,,.
(1)求证:;
(2)在不添加辅助线的情况下,请直接写出图中与面积相等的所有三角形(除外).
20.如图,已知BD是 ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ADE≌△CBF;
(2)连结CE,AF,求证:四边形AFCE为平行四边形.
参考答案
1.A
2.D
3.B
4.C
5.D
6.A
7.C
8.B
9.C
10.A
11.20
12.两组对边分别相等的四边形是平行四边形.
13.5
14.2
15.10
16.如图,连接BE,DF.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴DE∥BF.
17.(1)①作∠CBQ的平分线BP;②过点D作BP的垂线;
(2)∵BP//CE,∴∠ECD=∠FBD,∠CED=∠BFD,∵点D是BC的中点,∴CD=BD,∴△CDE≌△BDF,∴CE=BF,∵BF//CE,BF=CE,∴四边形BFCE是平行四边形.
18.(1)解:证明:四边形是平行四边形,
,,
,,
是的中位线,
,,
为的中点,
,
,,
,
四边形是平行四边形;
(2)解:四边形是平行四边形,
,
,
,
,
.
19.(1)∵点为的中点
∴
∵
∴CD=AE
∵
∴四边形ADCE是平行四边形
∴,AD∥CE
∴
∵,,,
∴(SAS)
(2)∵
∴与面积相等;
∵∵点为的中点
∴
∵与高相等
∴与面积相等;
∵
∴CD=AE,CD=EB
∵与高相等
∴与面积相等;
∵与高相等
∴与面积相等;
∴与面积相等的三角形有:、、、.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥AD,
∴∠EAD=90°,同理∠BCF=90°.
∴∠EAD=∠BCF.
在△AED和△CFB中
∠ADB=∠CBD,AD=BC,∠EAD=∠BCF,
∴△ADE≌△CBF.
(2)结论:四边形AECF是平行四边形.
理由:连接AC,
∵四边形ABCD是平行四边形,
∴AC平分BD,
由(1)△ADE≌△CBF,
∴AE=CF,∠AED=∠BFC,
∴AE∥CF,
∴四边形AECF是平行四边形.
