人教版八年级下册 18.2.1矩形基础练习 含答案
文档属性
| 名称 | 人教版八年级下册 18.2.1矩形基础练习 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 542.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览



文档简介
18.2.1矩形 基础练习
一、单选题
1.如图,四边形的对角线互相平分,若,则四边形为( )
A.菱形 B.矩形 C.菱形或矩形 D.无法判断
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
4.如图(1)是一副七巧板,其中最小正方形的边长是1,取其中六块拼成如图(2)的形状,沿图形外围构造矩形(虚线部分),则该矩形的面积是( )
A.35 B.35.5 C. D.
5.如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且,连接.若,则的长为( )
A. B.3 C.4 D.5
6.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形中,的平分线交边于点,于点,则下列结论错误的是( )
A. B. C. D.
7.如图,在矩形ABCD中,对角线AC, BD相交于点O,若边AB的长不变,边BC的长逐渐增大,下列说法正确的是( )
A.边CD的长也逐渐增大 B.∠AOB也逐渐增大
C.边OD的长也逐渐增大 D.∠ACB也逐渐增大
8.如图,中,,,点D为直线AC上一动点,连接BD,E在线段BD上,若,则的值( )
A.小于零 B.大于零 C.小于等于零 D.大于等于零
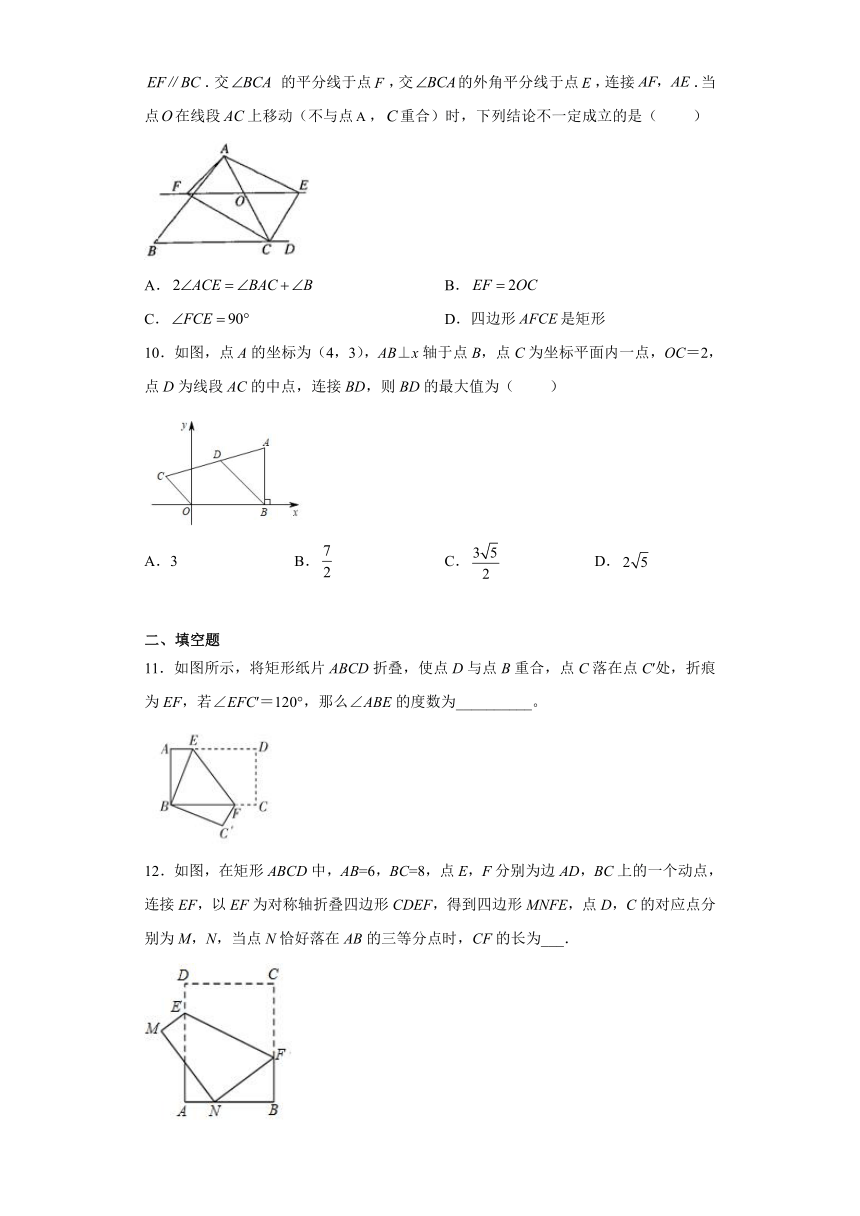
9.如图,点在边的延长线上,点是边上一个动点,过点作直线.交 的平分线于点,交的外角平分线于点,连接.当点在线段上移动(不与点,重合)时,下列结论不一定成立的是( )
A. B.
C. D.四边形是矩形
10.如图,点A的坐标为(4,3),AB⊥x轴于点B,点C为坐标平面内一点,OC=2,点D为线段AC的中点,连接BD,则BD的最大值为( )
A.3 B. C. D.
二、填空题
11.如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为__________。
12.如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
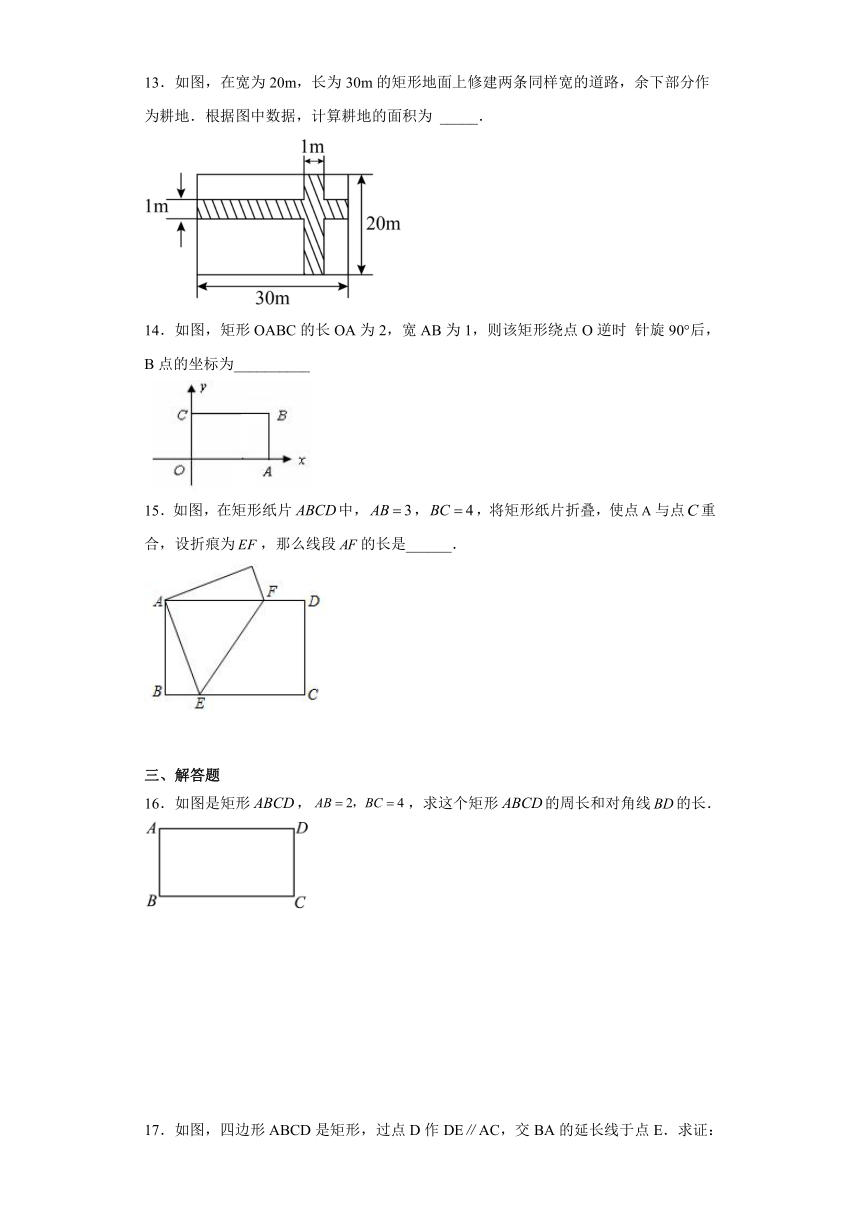
13.如图,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为 _____.
14.如图,矩形OABC的长OA为2,宽AB为1,则该矩形绕点O逆时 针旋90°后,B点的坐标为__________
15.如图,在矩形纸片中,,,将矩形纸片折叠,使点与点重合,设折痕为,那么线段的长是______.
三、解答题
16.如图是矩形,,求这个矩形的周长和对角线的长.
17.如图,四边形ABCD是矩形,过点D作DE∥AC,交BA的延长线于点E.求证:∠BDA =∠EDA.
18.如图,将AB=5cm,AD=4cm的长方形ABCD,沿过顶点A的直线AP为折痕折叠,使顶点B落在边CD上的点q处,
(1)求DQ的长;
(2)求AP:PB.
19.如图,在中,为的中点,连接并延长交的延长线于点,连接,若.
(1)求证:四边形是矩形;
(2)若,,直接写出的面积.
20.如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=4,∠BCE=30°.
(1)求线段EC的长;
(2)求证:∠EMC=2∠AEM;
(3)如果EM=8-AE,求△AEM的面积.
参考答案
1.B
2.B
3.B
4.B
5.A
6.C
7.C
8.D
9.D
10.B
11.30°
12.5或.
13.551/551平方米
14.(-1, 2)
15.
16.矩形的周长为12,
17.∵ 四边形ABCD是矩形,
∴ AC=BD,OA=,OD=,
∴ OA=OD,
∴ ∠CAD=∠BDA.
∵DE∥AC,
∴∠CAD=∠EDA,
∴∠BDA =∠EDA
18.解:(1)由折叠的性质可知△ABP≌AQP,
∴AB=AQ=5,
∵四边形ABCD是矩形,
∴∠D=90°,
∵AD=4cm,
∴DQ==3cm,
∴线段DQ的长度是3cm;
(2)由(1)可知DQ=3,
∴CQ=DC DQ=2,
设PQ=x,则PB=PQ=x,
∴CP=BC BP=4 x,
在Rt△CPQ中,PQ2=CQ2+CP2
∴x2=22+(4 x)2,
解得:x=2.5,
∴线段PQ的长度是2.5.
∴PB=2.5,
∴AP=,
∴AP:PB=.
19.(1)证明:∵四边形是平行四边形,
∴,
∴,
∵为的中点,
∴,
在和中,
,
∴,
∴.
∵,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形.
(2)解:∵,
∴,
∵.
∴是等边三角形,
∴,
∴,
∴的面积.
20. (1)解:点为边的中点,,
,
四边形是平行四边形,
,
,
,
.
(2)
证明:如图,延长,相交于点,
四边形是平行四边形,
,
,
在和中,,
,
,
是的斜边上的中线,
,
,
.
(3)解:如图,延长,相交于点,过点作,交延长线于点,
由(2)已证:,
,
设,则,
,
由(1)已得:,
,
在中,,即,
解得,
即,
,
,
四边形是平行四边形,
,
,
,
,
则的面积为.
一、单选题
1.如图,四边形的对角线互相平分,若,则四边形为( )
A.菱形 B.矩形 C.菱形或矩形 D.无法判断
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
4.如图(1)是一副七巧板,其中最小正方形的边长是1,取其中六块拼成如图(2)的形状,沿图形外围构造矩形(虚线部分),则该矩形的面积是( )
A.35 B.35.5 C. D.
5.如图,在矩形中,对角线相交于点O,点E是边的中点,点F在对角线上,且,连接.若,则的长为( )
A. B.3 C.4 D.5
6.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形中,的平分线交边于点,于点,则下列结论错误的是( )
A. B. C. D.
7.如图,在矩形ABCD中,对角线AC, BD相交于点O,若边AB的长不变,边BC的长逐渐增大,下列说法正确的是( )
A.边CD的长也逐渐增大 B.∠AOB也逐渐增大
C.边OD的长也逐渐增大 D.∠ACB也逐渐增大
8.如图,中,,,点D为直线AC上一动点,连接BD,E在线段BD上,若,则的值( )
A.小于零 B.大于零 C.小于等于零 D.大于等于零
9.如图,点在边的延长线上,点是边上一个动点,过点作直线.交 的平分线于点,交的外角平分线于点,连接.当点在线段上移动(不与点,重合)时,下列结论不一定成立的是( )
A. B.
C. D.四边形是矩形
10.如图,点A的坐标为(4,3),AB⊥x轴于点B,点C为坐标平面内一点,OC=2,点D为线段AC的中点,连接BD,则BD的最大值为( )
A.3 B. C. D.
二、填空题
11.如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为__________。
12.如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
13.如图,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为 _____.
14.如图,矩形OABC的长OA为2,宽AB为1,则该矩形绕点O逆时 针旋90°后,B点的坐标为__________
15.如图,在矩形纸片中,,,将矩形纸片折叠,使点与点重合,设折痕为,那么线段的长是______.
三、解答题
16.如图是矩形,,求这个矩形的周长和对角线的长.
17.如图,四边形ABCD是矩形,过点D作DE∥AC,交BA的延长线于点E.求证:∠BDA =∠EDA.
18.如图,将AB=5cm,AD=4cm的长方形ABCD,沿过顶点A的直线AP为折痕折叠,使顶点B落在边CD上的点q处,
(1)求DQ的长;
(2)求AP:PB.
19.如图,在中,为的中点,连接并延长交的延长线于点,连接,若.
(1)求证:四边形是矩形;
(2)若,,直接写出的面积.
20.如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=4,∠BCE=30°.
(1)求线段EC的长;
(2)求证:∠EMC=2∠AEM;
(3)如果EM=8-AE,求△AEM的面积.
参考答案
1.B
2.B
3.B
4.B
5.A
6.C
7.C
8.D
9.D
10.B
11.30°
12.5或.
13.551/551平方米
14.(-1, 2)
15.
16.矩形的周长为12,
17.∵ 四边形ABCD是矩形,
∴ AC=BD,OA=,OD=,
∴ OA=OD,
∴ ∠CAD=∠BDA.
∵DE∥AC,
∴∠CAD=∠EDA,
∴∠BDA =∠EDA
18.解:(1)由折叠的性质可知△ABP≌AQP,
∴AB=AQ=5,
∵四边形ABCD是矩形,
∴∠D=90°,
∵AD=4cm,
∴DQ==3cm,
∴线段DQ的长度是3cm;
(2)由(1)可知DQ=3,
∴CQ=DC DQ=2,
设PQ=x,则PB=PQ=x,
∴CP=BC BP=4 x,
在Rt△CPQ中,PQ2=CQ2+CP2
∴x2=22+(4 x)2,
解得:x=2.5,
∴线段PQ的长度是2.5.
∴PB=2.5,
∴AP=,
∴AP:PB=.
19.(1)证明:∵四边形是平行四边形,
∴,
∴,
∵为的中点,
∴,
在和中,
,
∴,
∴.
∵,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形.
(2)解:∵,
∴,
∵.
∴是等边三角形,
∴,
∴,
∴的面积.
20. (1)解:点为边的中点,,
,
四边形是平行四边形,
,
,
,
.
(2)
证明:如图,延长,相交于点,
四边形是平行四边形,
,
,
在和中,,
,
,
是的斜边上的中线,
,
,
.
(3)解:如图,延长,相交于点,过点作,交延长线于点,
由(2)已证:,
,
设,则,
,
由(1)已得:,
,
在中,,即,
解得,
即,
,
,
四边形是平行四边形,
,
,
,
,
则的面积为.
