人教版数学八年级下册18.2.3正方形 基础练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.3正方形 基础练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览


文档简介
18.2.3正方形基础练习
一、单选题
1.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是()
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
2.四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
3.下列命题中,假命题是( )
A.平行四边形的对角线互相垂直平分
B.矩形的对角线相等
C.菱形的面积等于两条对角线乘积的一半
D.对角线相等的菱形是正方形
4.若正方形ABCD各边的中点依次为E、F、G、H,则四边形EFGH是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
A.由小变大 B.由大变小
C.始终不变 D.先由大变小,然后又由小变大
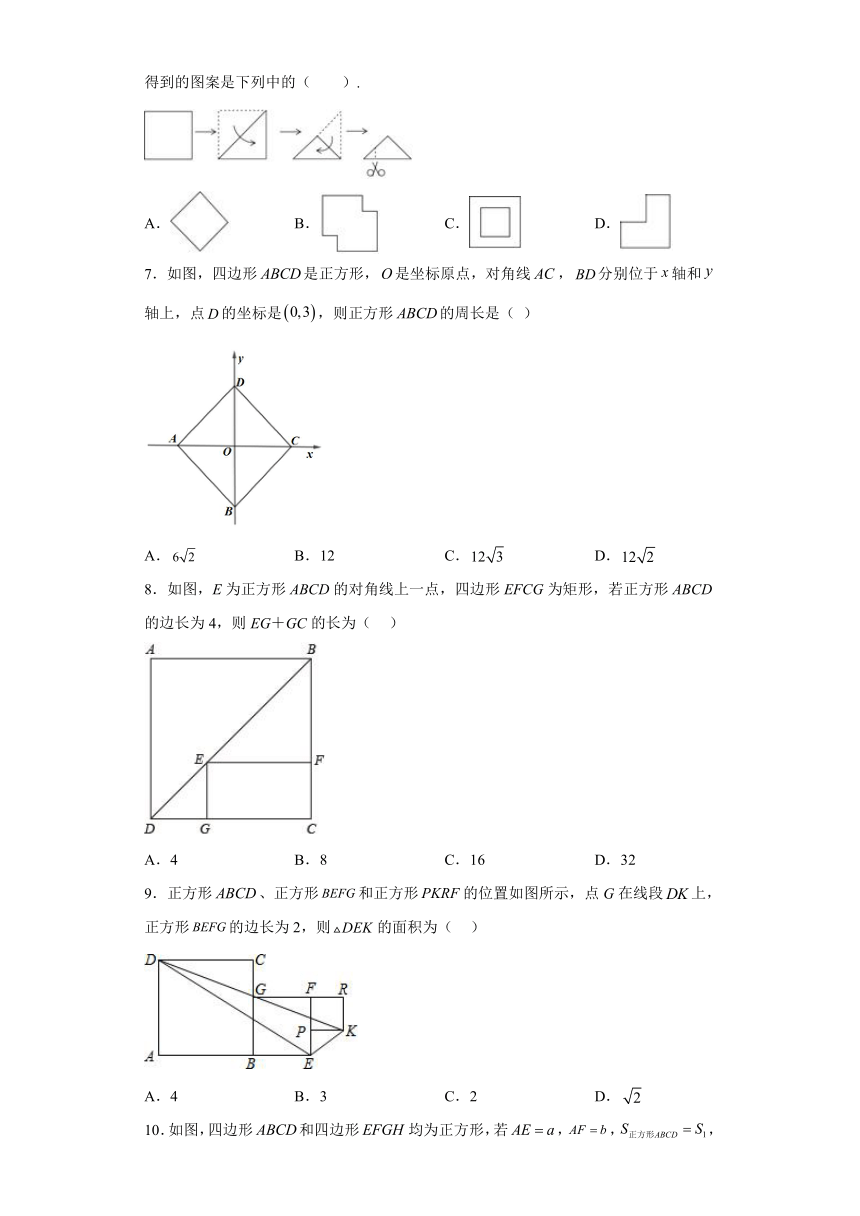
6.将一个正方形纸片按如图所示的方式进行折叠两次,在最后的三角形中按虚线剪开,得到的图案是下列中的( ).
A. B. C. D.
7.如图,四边形是正方形,是坐标原点,对角线,分别位于轴和轴上,点的坐标是,则正方形的周长是( )
A. B.12 C. D.
8.如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
9.正方形、正方形和正方形的位置如图所示,点G在线段上,正方形的边长为2,则的面积为( )
A.4 B.3 C.2 D.
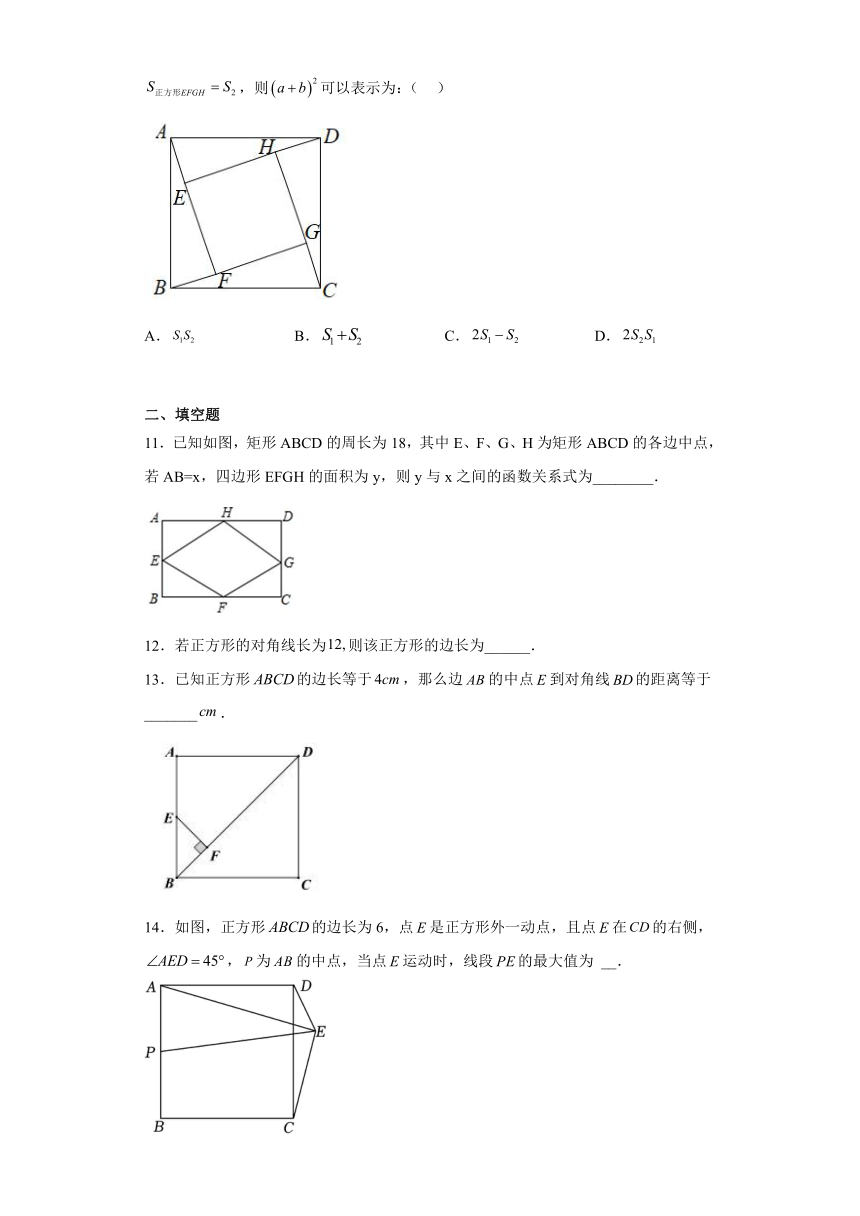
10.如图,四边形和四边形均为正方形,若,,,,则可以表示为:( )
A. B. C. D.
二、填空题
11.已知如图,矩形ABCD的周长为18,其中E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y,则y与x之间的函数关系式为________.
12.若正方形的对角线长为则该正方形的边长为______.
13.已知正方形的边长等于,那么边的中点到对角线的距离等于_______.
14.如图,正方形的边长为6,点是正方形外一动点,且点在的右侧,,为的中点,当点运动时,线段的最大值为 __.
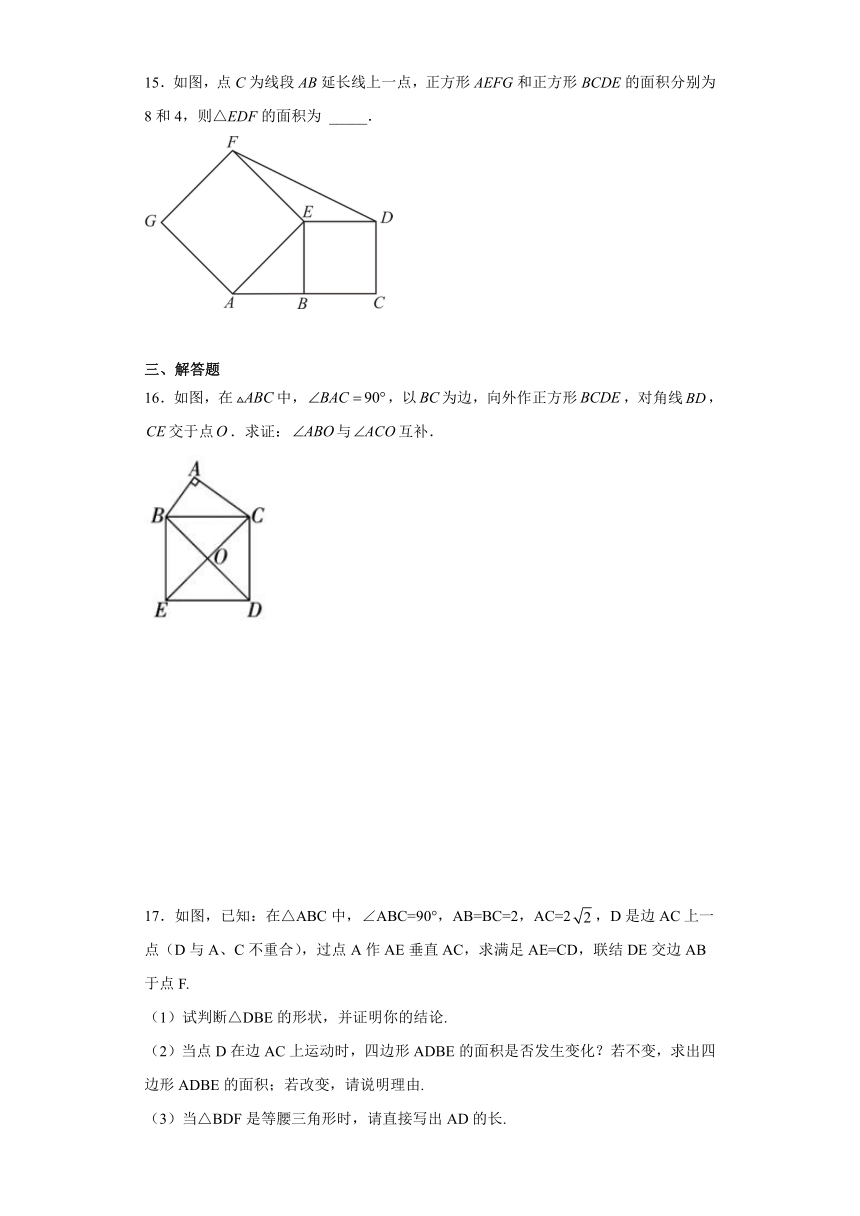
15.如图,点C为线段AB延长线上一点,正方形AEFG和正方形BCDE的面积分别为8和4,则△EDF的面积为 _____.
三、解答题
16.如图,在中,,以为边,向外作正方形,对角线,交于点.求证:与互补.
17.如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,AC=2,D是边AC上一点(D与A、C不重合),过点A作AE垂直AC,求满足AE=CD,联结DE交边AB于点F.
(1)试判断△DBE的形状,并证明你的结论.
(2)当点D在边AC上运动时,四边形ADBE的面积是否发生变化?若不变,求出四边形ADBE的面积;若改变,请说明理由.
(3)当△BDF是等腰三角形时,请直接写出AD的长.
18.如图所示,过正方形对角线上一点,作于点,作于点,试说明:.
19.正方形内部,,求证.
20.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
参考答案
1.D
2.A
3.A
4.D
5.C
6.B
7.D
8.A
9.A
10.C
11.
12.
13.
14.
15.2
16.证明:由四边形的内角和为360°可得四边形的内角和为,
四边形是正方形,
,
,
,
与互补.
17.(1)△DBE是等腰直角三角形.
理由:∵∠ABC=90°,AB=BC=2,
∴∠CAB=∠ACB=45°.
∵AE⊥AC,
∴∠EAC=90°,
∴∠BAE=45°.
在△CBD与△ABE中,
∵,
∴△CBD≌△ABE(SAS),
∴BD=BE,∠CBD=∠ABE,
∵∠CBD+∠ABD=90°,
∴∠ABE+∠ABD=90°,
即∠BDE=90°,
即△DBE是等腰直角三角形;
(2)不变.
∵由(1)知△CBD≌△ABE,
∴S四边形ADBE=S△ABC=×2×2=2;
(3)当BF=DF时,则∠BDE=∠FBD,
∵△DBE是等腰直角三角形,
∴∠BDE=45°,
∴∠FBD=45°
∴∠CBD=45°,
∴∠CBD=∠ABD,
∴AD=CD,
∴AD=AC,
∵AB=BC=2,
∴AC=2
∴AD=;
当BD=DF时,
∵△ABC是等腰直角三角形,△BDE是等腰直角三角形,
∴∠C=∠CAB=45°,∠BDE=∠BED=45°,
∴∠C=∠BDE,
∵∠ADB=∠C+∠CBD=∠BDE+∠FDA,
∴∠CDB=∠ADF,
在△BCD和△DAF中
∴△BCD≌△DAF(AAS),
∴AD=BC=2.
∴当△BDF是等腰三角形时,AD的长为或2.
18.证明:如图,连接,
∵四边形是正方形,,,
∴,,
∴四边形是矩形,
∴,
在与中,
,
∴
∴,
∴.
19.证明:分别把和平移,如图.
∵四边形是正方形,
∴,
∴.
∵
∴,
∴,
∴.
在与中,
∴,
∴,
∴.
20.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
一、单选题
1.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是()
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
2.四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
3.下列命题中,假命题是( )
A.平行四边形的对角线互相垂直平分
B.矩形的对角线相等
C.菱形的面积等于两条对角线乘积的一半
D.对角线相等的菱形是正方形
4.若正方形ABCD各边的中点依次为E、F、G、H,则四边形EFGH是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
A.由小变大 B.由大变小
C.始终不变 D.先由大变小,然后又由小变大
6.将一个正方形纸片按如图所示的方式进行折叠两次,在最后的三角形中按虚线剪开,得到的图案是下列中的( ).
A. B. C. D.
7.如图,四边形是正方形,是坐标原点,对角线,分别位于轴和轴上,点的坐标是,则正方形的周长是( )
A. B.12 C. D.
8.如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A.4 B.8 C.16 D.32
9.正方形、正方形和正方形的位置如图所示,点G在线段上,正方形的边长为2,则的面积为( )
A.4 B.3 C.2 D.
10.如图,四边形和四边形均为正方形,若,,,,则可以表示为:( )
A. B. C. D.
二、填空题
11.已知如图,矩形ABCD的周长为18,其中E、F、G、H为矩形ABCD的各边中点,若AB=x,四边形EFGH的面积为y,则y与x之间的函数关系式为________.
12.若正方形的对角线长为则该正方形的边长为______.
13.已知正方形的边长等于,那么边的中点到对角线的距离等于_______.
14.如图,正方形的边长为6,点是正方形外一动点,且点在的右侧,,为的中点,当点运动时,线段的最大值为 __.
15.如图,点C为线段AB延长线上一点,正方形AEFG和正方形BCDE的面积分别为8和4,则△EDF的面积为 _____.
三、解答题
16.如图,在中,,以为边,向外作正方形,对角线,交于点.求证:与互补.
17.如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,AC=2,D是边AC上一点(D与A、C不重合),过点A作AE垂直AC,求满足AE=CD,联结DE交边AB于点F.
(1)试判断△DBE的形状,并证明你的结论.
(2)当点D在边AC上运动时,四边形ADBE的面积是否发生变化?若不变,求出四边形ADBE的面积;若改变,请说明理由.
(3)当△BDF是等腰三角形时,请直接写出AD的长.
18.如图所示,过正方形对角线上一点,作于点,作于点,试说明:.
19.正方形内部,,求证.
20.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
参考答案
1.D
2.A
3.A
4.D
5.C
6.B
7.D
8.A
9.A
10.C
11.
12.
13.
14.
15.2
16.证明:由四边形的内角和为360°可得四边形的内角和为,
四边形是正方形,
,
,
,
与互补.
17.(1)△DBE是等腰直角三角形.
理由:∵∠ABC=90°,AB=BC=2,
∴∠CAB=∠ACB=45°.
∵AE⊥AC,
∴∠EAC=90°,
∴∠BAE=45°.
在△CBD与△ABE中,
∵,
∴△CBD≌△ABE(SAS),
∴BD=BE,∠CBD=∠ABE,
∵∠CBD+∠ABD=90°,
∴∠ABE+∠ABD=90°,
即∠BDE=90°,
即△DBE是等腰直角三角形;
(2)不变.
∵由(1)知△CBD≌△ABE,
∴S四边形ADBE=S△ABC=×2×2=2;
(3)当BF=DF时,则∠BDE=∠FBD,
∵△DBE是等腰直角三角形,
∴∠BDE=45°,
∴∠FBD=45°
∴∠CBD=45°,
∴∠CBD=∠ABD,
∴AD=CD,
∴AD=AC,
∵AB=BC=2,
∴AC=2
∴AD=;
当BD=DF时,
∵△ABC是等腰直角三角形,△BDE是等腰直角三角形,
∴∠C=∠CAB=45°,∠BDE=∠BED=45°,
∴∠C=∠BDE,
∵∠ADB=∠C+∠CBD=∠BDE+∠FDA,
∴∠CDB=∠ADF,
在△BCD和△DAF中
∴△BCD≌△DAF(AAS),
∴AD=BC=2.
∴当△BDF是等腰三角形时,AD的长为或2.
18.证明:如图,连接,
∵四边形是正方形,,,
∴,,
∴四边形是矩形,
∴,
在与中,
,
∴
∴,
∴.
19.证明:分别把和平移,如图.
∵四边形是正方形,
∴,
∴.
∵
∴,
∴,
∴.
在与中,
∴,
∴,
∴.
20.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
