有理数的加法[上学期]

课件18张PPT。有理数的加法４1、下列各组数中，哪一个数的绝对值大？
（１）７和４；　　　（２）－７和４；
（３）７和－４；　　（４）－７和－４．一．复习提问：３、根据上述问题回答：　⑴小亮两次一共前进了几米？　　（３米）　⑵北京的气温两天一共上升了几度？⑶东方汽车一共向东走了几米？（２度）（2米）２、说明下列用负数表示的量的实际意义：
　　⑴　小亮第一次向东前进了５米，接着按同一方向又前进了-2米;
　　⑵北京的气温第一天上升3０C，第二天又上升了－１０Ｃ；
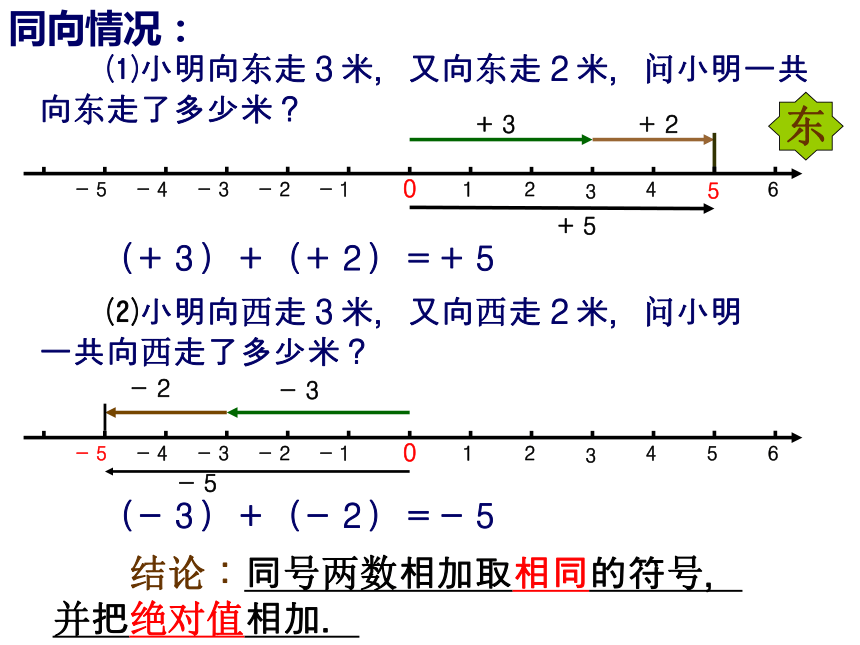
　　⑶东方汽车向东走了４千米之后，再向东走了－２千米．二、动态演示　分类归纳　总结法则问题一：　　在东西走向的马路上，小明从Ｏ点出发第一次走５米，第二次直线又走了３米，问：小明两次一共向东走了多少米？同向情况：　　⑴小明向东走３米，又向东走２米，问小明一共向东走了多少米？＋３＋２＋５东（＋３）＋（＋２）＝＋５　　⑵小明向西走３米，又向西走２米，问小明一共向西走了多少米？－３－２－５（－３）＋（－２）＝－５　　结论：同号两数相加取相同的符号，并把绝对值相加．异向情况：　　⑶在东西走向的马路上，小明向东走3米，
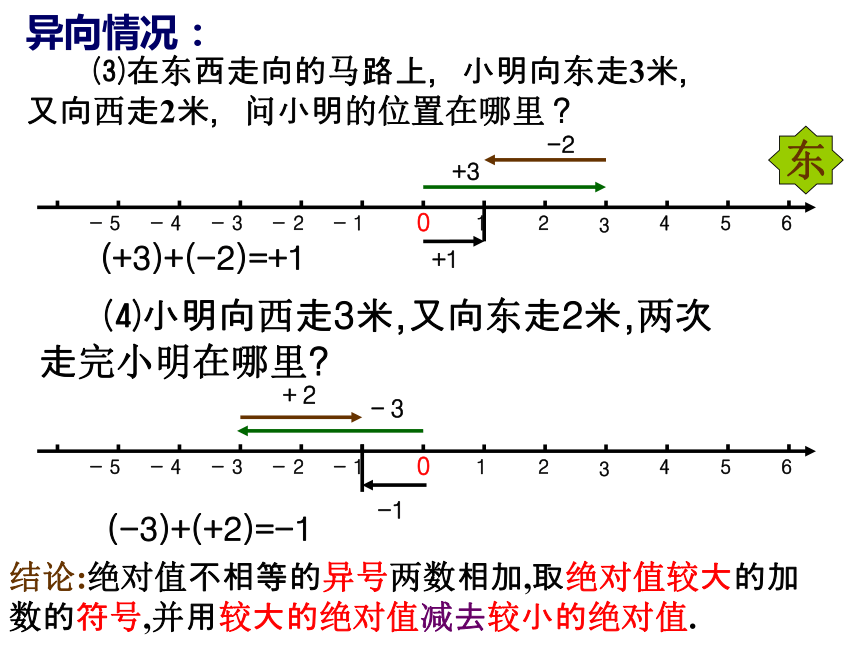
又向西走2米，问小明的位置在哪里？+3-2+1(+3)+(-2)=+1 ⑷小明向西走3米,又向东走2米,两次走完小明在哪里?东-３+２-1(-3)+(+2)=-1结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.问题二： 在东西走向的马路上，小明从Ｏ点出发向东走3米，又向东走-3米，两次一共向东走了多少米？
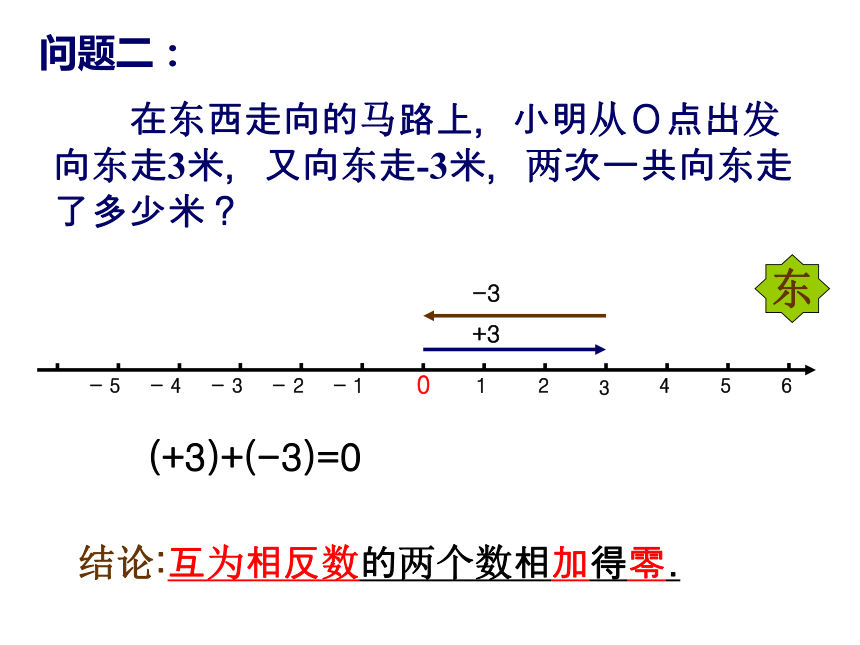
+3-3(+3)+(-3)=0结论:互为相反数的两个数相加得零.东问题三： 在东西走向的马路上，小明从Ｏ点出发向东走-3米，又向东走0米，两次一共向东走了多少米？-3(-3)+0=-3结论:一个数同零相加,仍得这个数.东有理数加法法则同号两数相加取相同的符号,并把绝对值相加;
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零.
一个数同零相加,仍得这个数.
三、分析特征 强化理解 总结步骤（-4）+（-8）=- （ 4 + 8 ）=-12同号两数相加取相同符号通过绝对值化归为算术数的加法（-9）+（+2）=- （ 9 – 2 ）=-7异号两数相加取绝对值较大的加数的符号通过绝对值化归为算术数的减法有理数加法运算步骤：
1、先判断类型（同号、异号等）；
2、再确定符号；
3、后进行绝对值的加减运算。
四、对比异同 强化记忆不谈符号，均是正数（除零）.
可正、可负、可为零.
比两个加数都大或相等.
可能比两个加数都大;
可能比两个加数都小;
可能大于其中一个加数而小于另一个加数.五、设置问题 强化关键判断正误并改错:
两个负数相加，应把绝对值相减；
正数加负数和一定为负；
负数加正数和一定为正；
两个有理数的和为负数时，这两个有理数都是负数.六、应用举例 巩固练习例题：计算下列各题:⑴ 180+（-10）； ⑵（-10）+（-1）；
⑶ 5+（-5）； ⑷ 0 +（-2）.练习一：口算下列各题，并说明理由．⑴（＋４）＋（＋７）；
⑵（－４）＋（－７）；
⑶（＋４）＋（－７）；
⑷（－４）＋（＋７）；
⑸（－４）＋（＋４）；
⑹（－９）＋０．（＋１１）（－１１）（－３）（＋３）（０）（－９）练习二：计算⑴　（－２５）＋（－７）；　　　　
⑵　（－１３）＋５；
⑶　（－２３）＋０；　　　　　　　
⑷　４５＋（－４５）．（－３２）（－８）（－２３）（０）练习三：用“＞”或“＜”填空：＞＜＞＜七、课堂小结　布置作业　小结：
本节课所学习的主要内容；
运用有理数加法法则的关键问题；
本节课涉及的数学思想方法．作业：
阅读课本Ｐ４４－Ｐ４８
做Ｐ４８习题２．４第１、２、３题；
思考题：