10.5 全等三角形学案
图片预览
文档简介
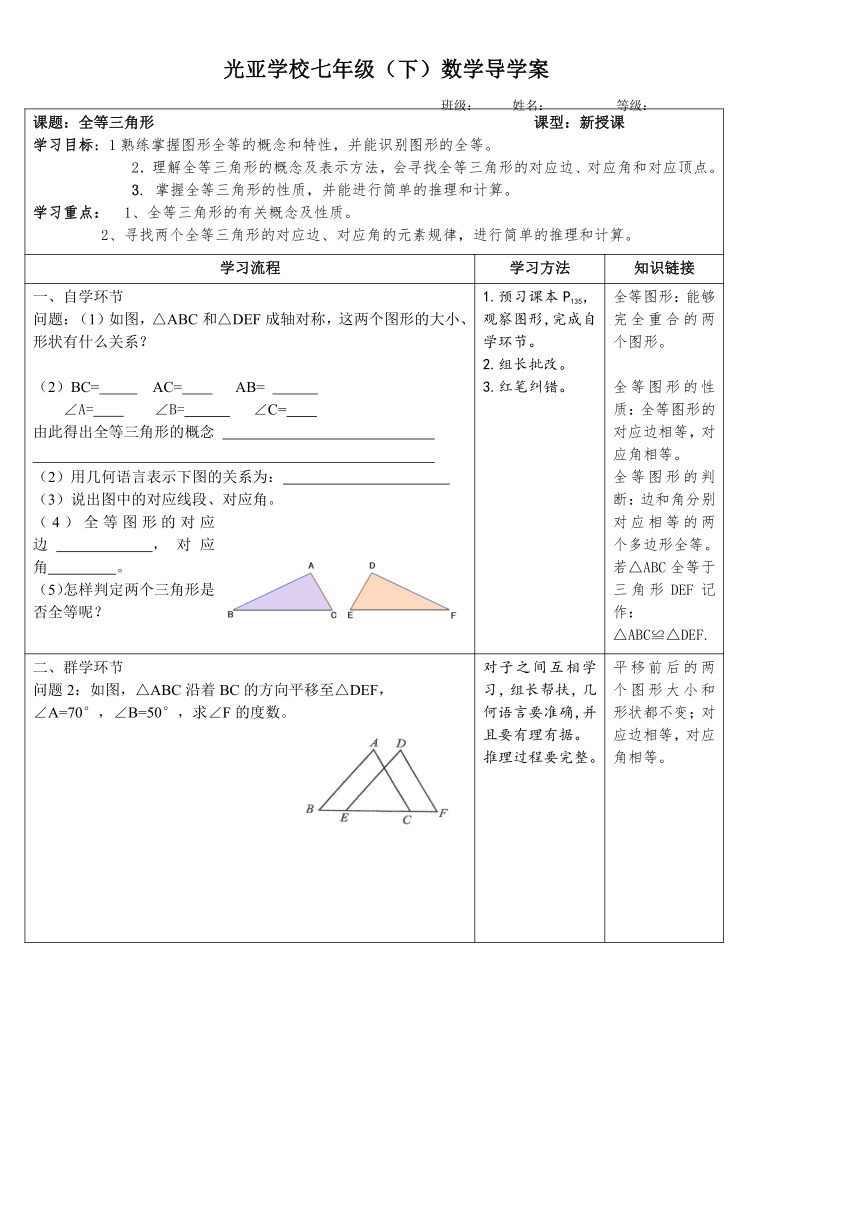
课题:全等三角形 课型:新授课学习目标:1熟练掌握图形全等的概念和特性,并能识别图形的全等。2.理解全等三角形的概念及表示方法,会寻找全等三角形的对应边、对应角和对应顶点。 3. 掌握全等三角形的性质,并能进行简单的推理和计算。学习重点: 1、全等三角形的有关概念及性质。2、寻找两个全等三角形的对应边、对应角的元素规律,进行简单的推理和计算。
学习流程 学习方法 知识链接
一、自学环节问题:(1)如图,△ABC和△DEF成轴对称,这两个图形的大小、形状有什么关系?(2)BC= AC= AB= ∠A= ∠B= ∠C= 由此得出全等三角形的概念 (2)用几何语言表示下图的关系为: (3)说出图中的对应线段、对应角。(4)全等图形的对应边 ,对应角 。(5)怎样判定两个三角形是否全等呢? 1.预习课本P135,观察图形,完成自学环节。2.组长批改。3.红笔纠错。 全等图形:能够完全重合的两个图形。全等图形的性质:全等图形的对应边相等,对应角相等。全等图形的判断:边和角分别对应相等的两个多边形全等。若△ABC全等于三角形DEF记作:△ABC≌△DEF.
二、群学环节问题2:如图,△ABC沿着BC的方向平移至△DEF,∠A=70°,∠B=50°,求∠F的度数。 对子之间互相学习,组长帮扶,几何语言要准确,并且要有理有据。推理过程要完整。 平移前后的两个图形大小和形状都不变;对应边相等,对应角相等。
三、展示环节 如图3,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长. 1.组长分工,确定两名板演人员,其他组员在座位上群学。(可从:已知条件及隐含条件、解题思路、解此题的关键等方面进行展示) 全等三角形的对应边相等,对应角相等。三角形的内角和等于180°。
四、点拨环节
五、课堂总结1.图形的三种基本变换是 ( http: / / www.21cnjy.com ) 、 、 ,图形经过这样的变换 发生了变换,但变换前后两个图形的 相等, 相等,图形的 和 并没有变。2.能够完全 的图形是全等图形,若△ABC和△A’B’C’是全等的图形记作 读作 。
六、达标检测(*分钟)必做1.如图1,若△ABC≌△EFC,且CF=3cm,CE=5cm,∠EFC=64°,则BC=_____cm, AF= cm,∠B=___.如图2,AC=DB,∠1=∠2, 则△ABC≌△______,∠ABC=∠______. 3、如图,已知△AOB≌△COD,∠AOB=∠COD,∠A=∠C,∠D的对应角是________,图中相等的线段有________________ _ _;除对顶角和上面已经写出的对应角外图中相等的角(小于平角的角)有 。4、如图,若△ABC≌△DEF,则∠E等于( ) A. 30° B. 50° C. 60° D. 100° HYPERLINK "http://www.21cnjy.com" 5.如上图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD, 则另外两组对应边为________选作:如右图, △ABC≌△AEC, ∠B=30°,∠ACB=85°,求出△AEC各角的度数。.
反思与收获:
光亚学校七年级(下)数学导学案
班级: 姓名: 等级:
A
C
D
B
O
学习流程 学习方法 知识链接
一、自学环节问题:(1)如图,△ABC和△DEF成轴对称,这两个图形的大小、形状有什么关系?(2)BC= AC= AB= ∠A= ∠B= ∠C= 由此得出全等三角形的概念 (2)用几何语言表示下图的关系为: (3)说出图中的对应线段、对应角。(4)全等图形的对应边 ,对应角 。(5)怎样判定两个三角形是否全等呢? 1.预习课本P135,观察图形,完成自学环节。2.组长批改。3.红笔纠错。 全等图形:能够完全重合的两个图形。全等图形的性质:全等图形的对应边相等,对应角相等。全等图形的判断:边和角分别对应相等的两个多边形全等。若△ABC全等于三角形DEF记作:△ABC≌△DEF.
二、群学环节问题2:如图,△ABC沿着BC的方向平移至△DEF,∠A=70°,∠B=50°,求∠F的度数。 对子之间互相学习,组长帮扶,几何语言要准确,并且要有理有据。推理过程要完整。 平移前后的两个图形大小和形状都不变;对应边相等,对应角相等。
三、展示环节 如图3,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长. 1.组长分工,确定两名板演人员,其他组员在座位上群学。(可从:已知条件及隐含条件、解题思路、解此题的关键等方面进行展示) 全等三角形的对应边相等,对应角相等。三角形的内角和等于180°。
四、点拨环节
五、课堂总结1.图形的三种基本变换是 ( http: / / www.21cnjy.com ) 、 、 ,图形经过这样的变换 发生了变换,但变换前后两个图形的 相等, 相等,图形的 和 并没有变。2.能够完全 的图形是全等图形,若△ABC和△A’B’C’是全等的图形记作 读作 。
六、达标检测(*分钟)必做1.如图1,若△ABC≌△EFC,且CF=3cm,CE=5cm,∠EFC=64°,则BC=_____cm, AF= cm,∠B=___.如图2,AC=DB,∠1=∠2, 则△ABC≌△______,∠ABC=∠______. 3、如图,已知△AOB≌△COD,∠AOB=∠COD,∠A=∠C,∠D的对应角是________,图中相等的线段有________________ _ _;除对顶角和上面已经写出的对应角外图中相等的角(小于平角的角)有 。4、如图,若△ABC≌△DEF,则∠E等于( ) A. 30° B. 50° C. 60° D. 100° HYPERLINK "http://www.21cnjy.com" 5.如上图所示,已知△ABC≌△ADE,∠C=∠E,AB=AD, 则另外两组对应边为________选作:如右图, △ABC≌△AEC, ∠B=30°,∠ACB=85°,求出△AEC各角的度数。.
反思与收获:
光亚学校七年级(下)数学导学案
班级: 姓名: 等级:
A
C
D
B
O
