人教版八年级数学下册 17.2勾股定理的逆定理强化训练卷(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.2勾股定理的逆定理强化训练卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 16:24:10 | ||
图片预览

文档简介
17.2 勾股定理的逆定理 强化训练卷
一、单选题
1.以下列各组数为三边的三角形中不是直角三角形的是( )
A.1、、2 B.6、10、8 C.3、4、5 D.6、5、4
2.在△ABC中,三边长a、b、c满足(a +c)(a-c) =,则△ABC的形状是( )
A.以a为斜边长的直角三角形 B.以b为斜边长的直角三角形
C.以c为斜边长的直角三角形 D.不是直角三角形
3.下列各组数中,能作为直角三角形的三边长的是( )
A.,,6 B.4,, C.,, D.,,
4.满足下列条件的不是直角三角形的是( )
A. B.
C. D.,,
5.△ABC的三边长a,b,c满足+(b﹣12)2+|c﹣13|=0,则△ABC的面积是( )
A.65 B.60 C.30 D.26
6.如图,在△ABC中,AB=10,BC=8,AC=6,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
7.由下列条件不能判定ABC为直角三角形的是( )
A. B.
C. D.,,
8.在中,,,的对边分别是,,,下列条件中,能判断是直角三角形的是( )
A. B.,,
C., D.
9.如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
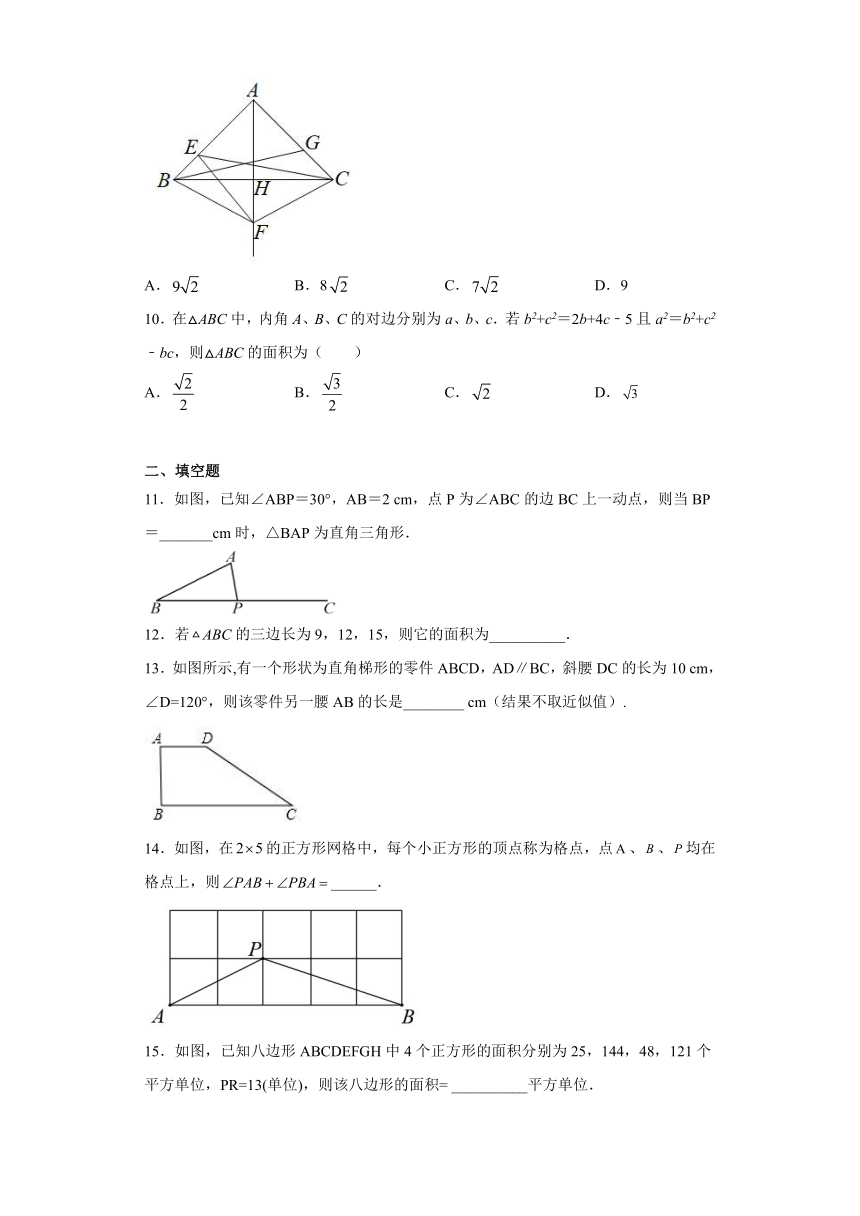
A. B.8 C. D.9
10.在△ABC中,内角A、B、C的对边分别为a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,则△ABC的面积为( )
A. B. C. D.
二、填空题
11.如图,已知∠ABP=30°,AB=2 cm,点P为∠ABC的边BC上一动点,则当BP=_______cm时,△BAP为直角三角形.
12.若ABC的三边长为9,12,15,则它的面积为__________.
13.如图所示,有一个形状为直角梯形的零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰AB的长是________ cm(结果不取近似值).
14.如图,在的正方形网格中,每个小正方形的顶点称为格点,点、、均在格点上,则______.
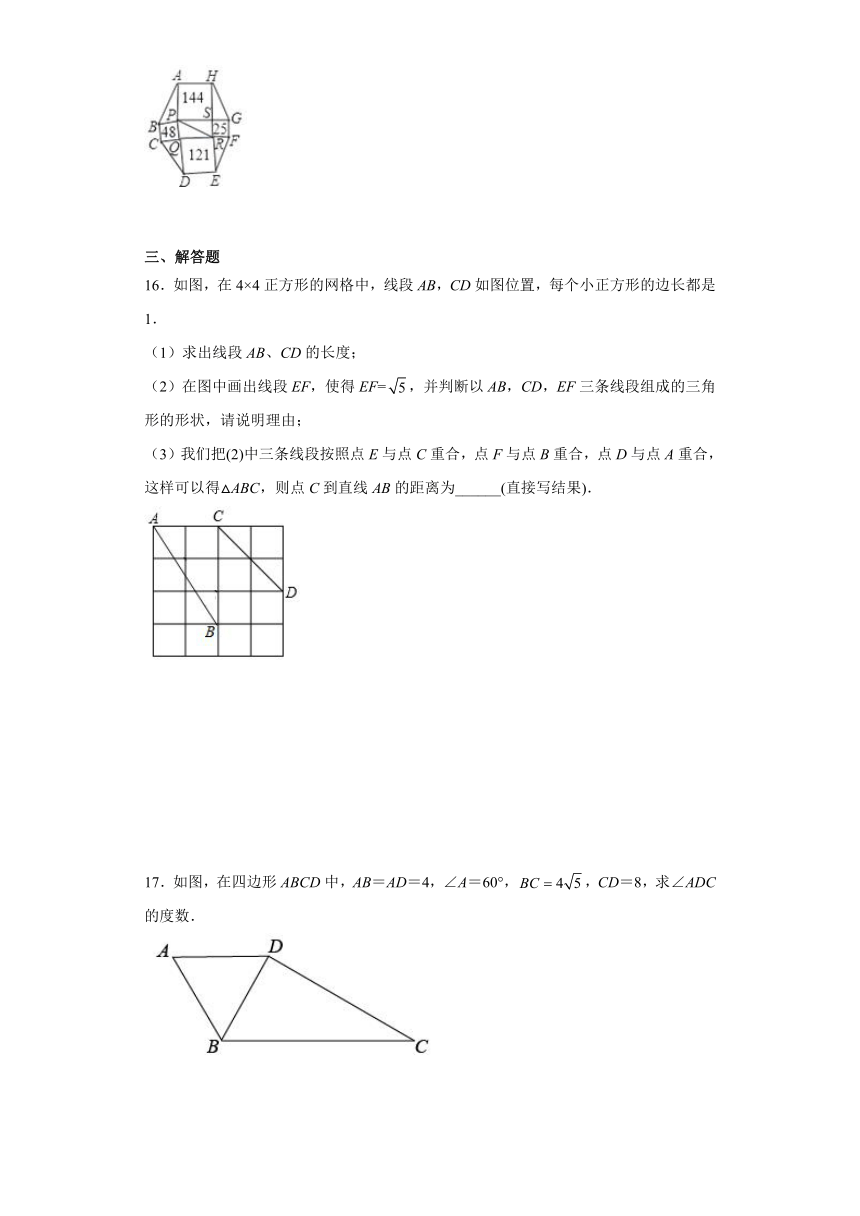
15.如图,已知八边形ABCDEFGH中4个正方形的面积分别为25,144,48,121个平方单位,PR=13(单位),则该八边形的面积= __________平方单位.
三、解答题
16.如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF=,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).
17.如图,在四边形ABCD中,AB=AD=4,∠A=60°,,CD=8,求∠ADC的度数.
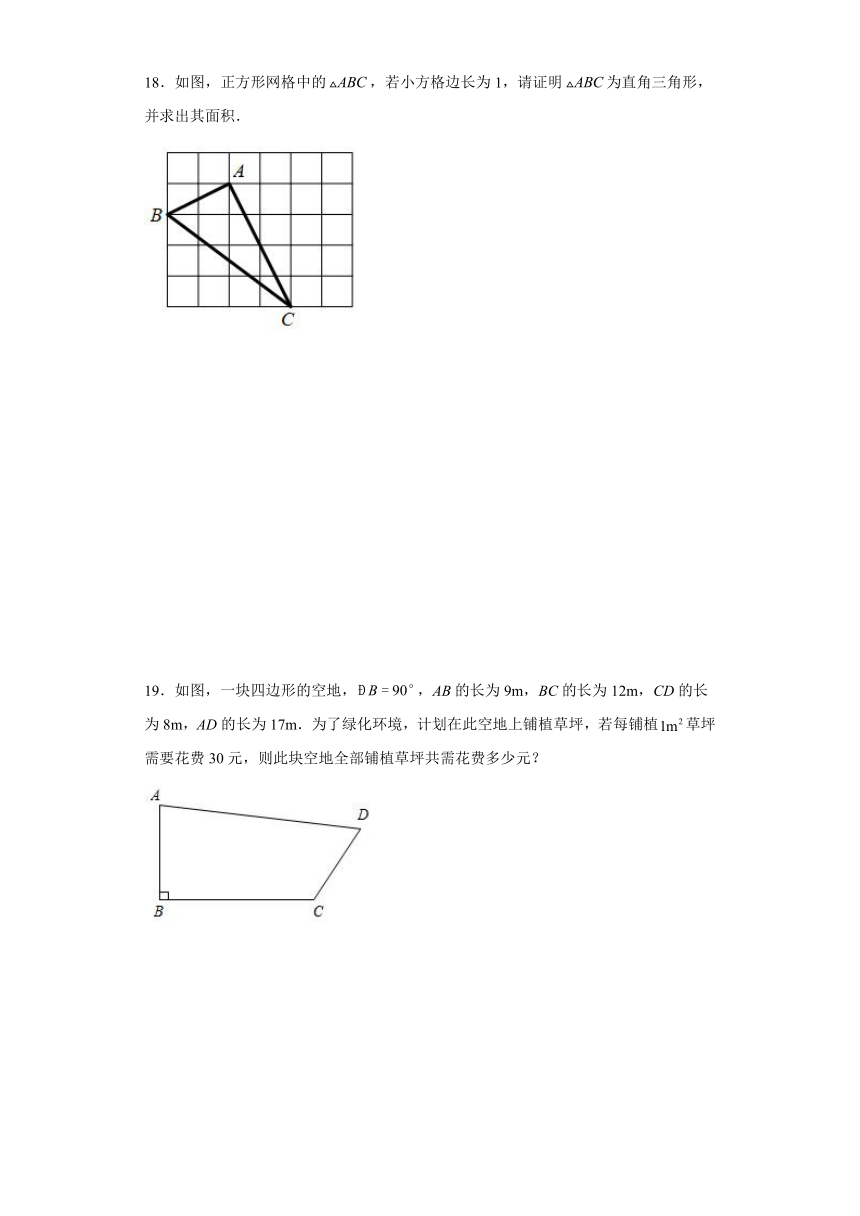
18.如图,正方形网格中的,若小方格边长为1,请证明为直角三角形,并求出其面积.
19.如图,一块四边形的空地,,AB的长为9m,BC的长为12m,CD的长为8m,AD的长为17m.为了绿化环境,计划在此空地上铺植草坪,若每铺植草坪需要花费30元,则此块空地全部铺植草坪共需花费多少元?
20.已知组正整数:第一组:3,4,5;第二组:8,6,10;第三组:15,8,17;第四组:24,10,26;第五组:35,12,37;第六组:48,14,50;…
(1)是否存在一组数,既符合上述规律,且其中一个数为71?若存在,请写出这组数;若不存在,请说明理由;
(2)以任意一个大于2的偶数为一条直角边的长,是否一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数?若可以,请说明理由;若不可以,请举出反例.
参考答案
1.D
2.A
3.C
4.A
5.C
6.B
7.D
8.D
9.D
10.B
11.或
12.54
13.cm.
14.45°/45度
15.428+66
16.解:(1)AB=,CD=;
(2)EF=,如图所示:
∵CD2+EF2=AB2
∴以AB,CD,EF三条线段组成的三角形是直角三角形;
(3)设C到直线AB的距离为h.
则有,
∴h=,
∴C到直线AB的距离为.
故答案为(1)AB=,CD=;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3).
17.解:∵AB=AD=4,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,BD=4,
∵BC=,CD=8.
∴BD2+CD2=42+82=16+64=80=()2,
∴△BDC是直角三角形,∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=60°+90°=150°,
即∠ADC的度数是150°.
18.解:∵,,,
∴,
∴是直角三角形,,
∵,,
∴的面积.
19.解:连接AC,在中,
∴,,
在中,∵,
∴,为直角三角形,
∴
∴
答:此块空地全部铺植草坪共需花费元.
20.(1)不存在一组数,既符合上述规律,且其中一个数为71.
理由如下:
根据题意可知,这组正整数符合规律,,(,且为整数).
若,则,此时不符合题意;
若,则,此时不符合题意;
若,则,此时不符合题意,
所以不存在一组数,既符合上述规律,且其中一个数为71.
(2)以任意一个大于2的偶数为一条直角边的长,一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数.
理由如下:
对于一组数:,,(,且为整数).
因为
所以若一个三角形三边长分别为,,(,且为整数),则该三角形为直角三角形.
因为当,且为整数时,表示任意一个大于2的偶数,,均为正整数,
所以以任意一个大于2的偶数为一条直角边的长,一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数.
一、单选题
1.以下列各组数为三边的三角形中不是直角三角形的是( )
A.1、、2 B.6、10、8 C.3、4、5 D.6、5、4
2.在△ABC中,三边长a、b、c满足(a +c)(a-c) =,则△ABC的形状是( )
A.以a为斜边长的直角三角形 B.以b为斜边长的直角三角形
C.以c为斜边长的直角三角形 D.不是直角三角形
3.下列各组数中,能作为直角三角形的三边长的是( )
A.,,6 B.4,, C.,, D.,,
4.满足下列条件的不是直角三角形的是( )
A. B.
C. D.,,
5.△ABC的三边长a,b,c满足+(b﹣12)2+|c﹣13|=0,则△ABC的面积是( )
A.65 B.60 C.30 D.26
6.如图,在△ABC中,AB=10,BC=8,AC=6,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
7.由下列条件不能判定ABC为直角三角形的是( )
A. B.
C. D.,,
8.在中,,,的对边分别是,,,下列条件中,能判断是直角三角形的是( )
A. B.,,
C., D.
9.如图,在三角形,,,是上中点,是射线上一点.是上一点,连接,,,点在上,连接,,,,则的长为( )
A. B.8 C. D.9
10.在△ABC中,内角A、B、C的对边分别为a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,则△ABC的面积为( )
A. B. C. D.
二、填空题
11.如图,已知∠ABP=30°,AB=2 cm,点P为∠ABC的边BC上一动点,则当BP=_______cm时,△BAP为直角三角形.
12.若ABC的三边长为9,12,15,则它的面积为__________.
13.如图所示,有一个形状为直角梯形的零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰AB的长是________ cm(结果不取近似值).
14.如图,在的正方形网格中,每个小正方形的顶点称为格点,点、、均在格点上,则______.
15.如图,已知八边形ABCDEFGH中4个正方形的面积分别为25,144,48,121个平方单位,PR=13(单位),则该八边形的面积= __________平方单位.
三、解答题
16.如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF=,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).
17.如图,在四边形ABCD中,AB=AD=4,∠A=60°,,CD=8,求∠ADC的度数.
18.如图,正方形网格中的,若小方格边长为1,请证明为直角三角形,并求出其面积.
19.如图,一块四边形的空地,,AB的长为9m,BC的长为12m,CD的长为8m,AD的长为17m.为了绿化环境,计划在此空地上铺植草坪,若每铺植草坪需要花费30元,则此块空地全部铺植草坪共需花费多少元?
20.已知组正整数:第一组:3,4,5;第二组:8,6,10;第三组:15,8,17;第四组:24,10,26;第五组:35,12,37;第六组:48,14,50;…
(1)是否存在一组数,既符合上述规律,且其中一个数为71?若存在,请写出这组数;若不存在,请说明理由;
(2)以任意一个大于2的偶数为一条直角边的长,是否一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数?若可以,请说明理由;若不可以,请举出反例.
参考答案
1.D
2.A
3.C
4.A
5.C
6.B
7.D
8.D
9.D
10.B
11.或
12.54
13.cm.
14.45°/45度
15.428+66
16.解:(1)AB=,CD=;
(2)EF=,如图所示:
∵CD2+EF2=AB2
∴以AB,CD,EF三条线段组成的三角形是直角三角形;
(3)设C到直线AB的距离为h.
则有,
∴h=,
∴C到直线AB的距离为.
故答案为(1)AB=,CD=;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3).
17.解:∵AB=AD=4,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,BD=4,
∵BC=,CD=8.
∴BD2+CD2=42+82=16+64=80=()2,
∴△BDC是直角三角形,∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=60°+90°=150°,
即∠ADC的度数是150°.
18.解:∵,,,
∴,
∴是直角三角形,,
∵,,
∴的面积.
19.解:连接AC,在中,
∴,,
在中,∵,
∴,为直角三角形,
∴
∴
答:此块空地全部铺植草坪共需花费元.
20.(1)不存在一组数,既符合上述规律,且其中一个数为71.
理由如下:
根据题意可知,这组正整数符合规律,,(,且为整数).
若,则,此时不符合题意;
若,则,此时不符合题意;
若,则,此时不符合题意,
所以不存在一组数,既符合上述规律,且其中一个数为71.
(2)以任意一个大于2的偶数为一条直角边的长,一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数.
理由如下:
对于一组数:,,(,且为整数).
因为
所以若一个三角形三边长分别为,,(,且为整数),则该三角形为直角三角形.
因为当,且为整数时,表示任意一个大于2的偶数,,均为正整数,
所以以任意一个大于2的偶数为一条直角边的长,一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数.
