第七章:平面直角坐标系练习题(含解析)2021-2022学年陕西省各地七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第七章:平面直角坐标系练习题(含解析)2021-2022学年陕西省各地七年级下学期人教版数学期末试题选编 |

|
|
| 格式 | zip | ||
| 文件大小 | 691.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 19:57:19 | ||
图片预览



文档简介
第七章:平面直角坐标系
一、单选题
1.(2022春·陕西渭南·七年级统考期末)若点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
2.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,若点P在第二象限,且点P到x轴的距离为1,到y轴的距离为2,则点P的坐标为( )
A. B. C. D.
3.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,第二象限内点的坐标为,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·陕西渭南·七年级统考期末)在平面直角坐标系中,若点在y轴上,则点的坐标为( )
A.(3,-3) B.(5,-1) C.(3,3) D.(5,1)
6.(2022春·陕西商洛·七年级校考期末)在平面直角坐标系中,点的坐标为,点的坐标为,则线段上任意一点的坐标可表示为( )
A. B.
C. D.
7.(2022春·陕西渭南·七年级统考期末)在一次“寻宝”游戏中,寻宝人已经找到两个标志点和,并且知道藏宝地点的坐标是,则藏宝处应为图中的( )
A.点 B.点 C.点 D.点
8.(2022春·陕西延安·七年级统考期末)如图,已知点A(2,3),B(5,1),若将线段AB平移至A1B1, A1在y轴正半轴上,B1在x轴上,则A1的纵坐标、B1的横坐标分别为( )
A.2,3 B.1,4 C.2,2 D.1,3
9.(2022春·陕西渭南·七年级统考期末)在平面直角坐标系中,将点先向左平移2个单位,再向下平移3个单位,则移动后得到的点的坐标是( )
A. B. C. D.
10.(2022春·陕西商洛·七年级统考期末)已知线段的端点,,将线段平移后,点坐标是,则点的坐标是( )
A. B. C. D.
二、填空题
11.(2022春·陕西宝鸡·七年级统考期末)在平面直角坐标系xOy中,若点P在第四象限,且点P到x轴和y轴距离分别为5和4,则点P的坐标为________________.
12.(2022春·陕西安康·七年级统考期末)已知平面直角坐标系中有一点M(m﹣1,2m+3),若点M到x轴的距离为1,则点M的坐标为_____.
13.(2022春·陕西安康·七年级统考期末)如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是______.
14.(2022春·陕西渭南·七年级统考期末)已知点,,,则点在第__________象限.
15.(2022春·陕西安康·七年级统考期末)将点向右平移3个单位后,落在轴上,则的值为______.
16.(2022春·陕西渭南·七年级统考期末)中华象棋文化博大精深,渊源深厚,如图所示,在象棋盘上建立平面直角坐标系,是“马”位于点,“炮”位于,写出“兵”所在位置的坐标_______.
17.(2022春·陕西渭南·七年级统考期末)如图,在平面直角坐标系中,将折线向右平移得到折线,则折线在平移过程中扫过的面积是______.
三、解答题
18.(2022春·陕西宝鸡·七年级统考期末)已知点.
(1)若点P在x轴上,求m的值;
(2)若点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
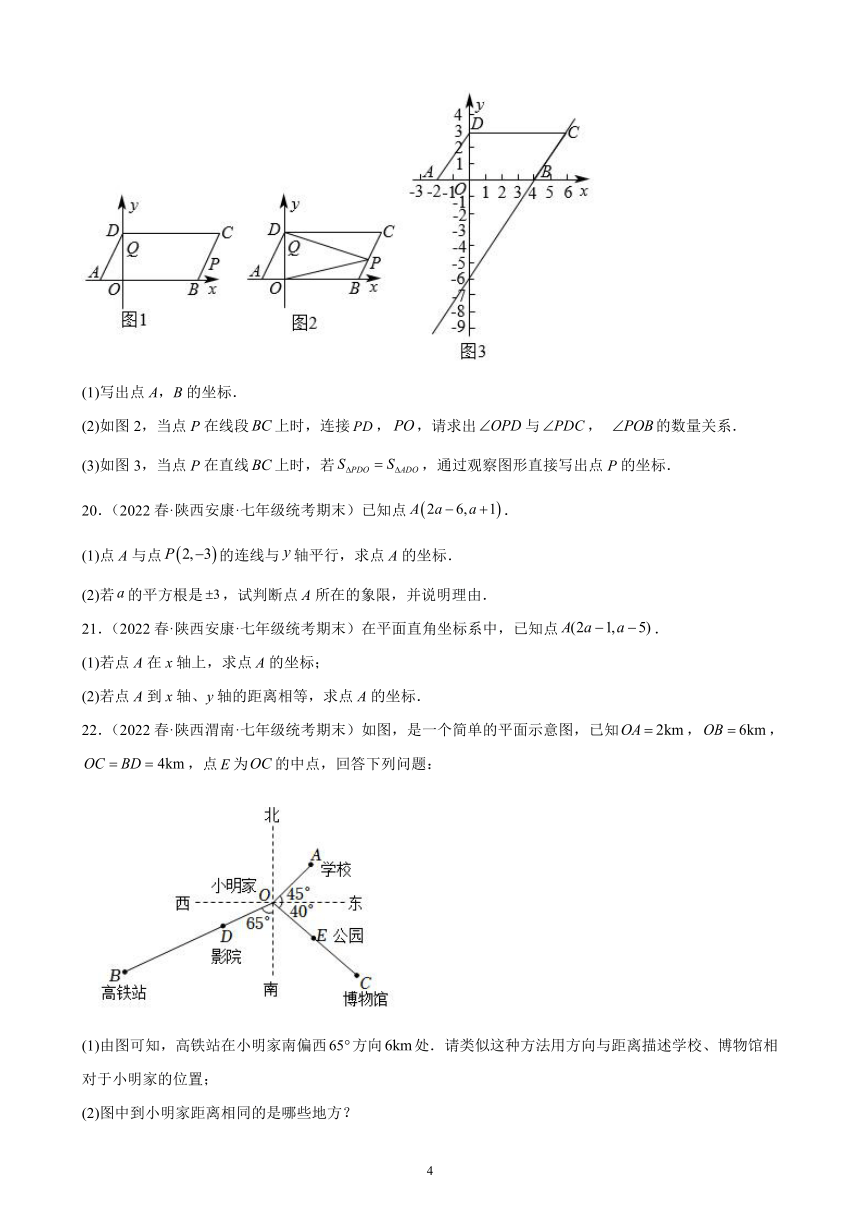
19.(2022春·陕西商洛·七年级校考期末)如图1,在平面直角坐标系中,点A,B的坐标分别是.且a、b满足现同时将点A,B分别向上平移3个单位长度,再向右平移2个单位长度,得到A,B的对应点D,C,连接,,.
(1)写出点A,B的坐标.
(2)如图2,当点P在线段上时,连接,,请求出与, 的数量关系.
(3)如图3,当点P在直线上时,若,通过观察图形直接写出点P的坐标.
20.(2022春·陕西安康·七年级统考期末)已知点.
(1)点A与点的连线与轴平行,求点A的坐标.
(2)若的平方根是,试判断点A所在的象限,并说明理由.
21.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,已知点.
(1)若点A在x轴上,求点A的坐标;
(2)若点A到x轴、y轴的距离相等,求点A的坐标.
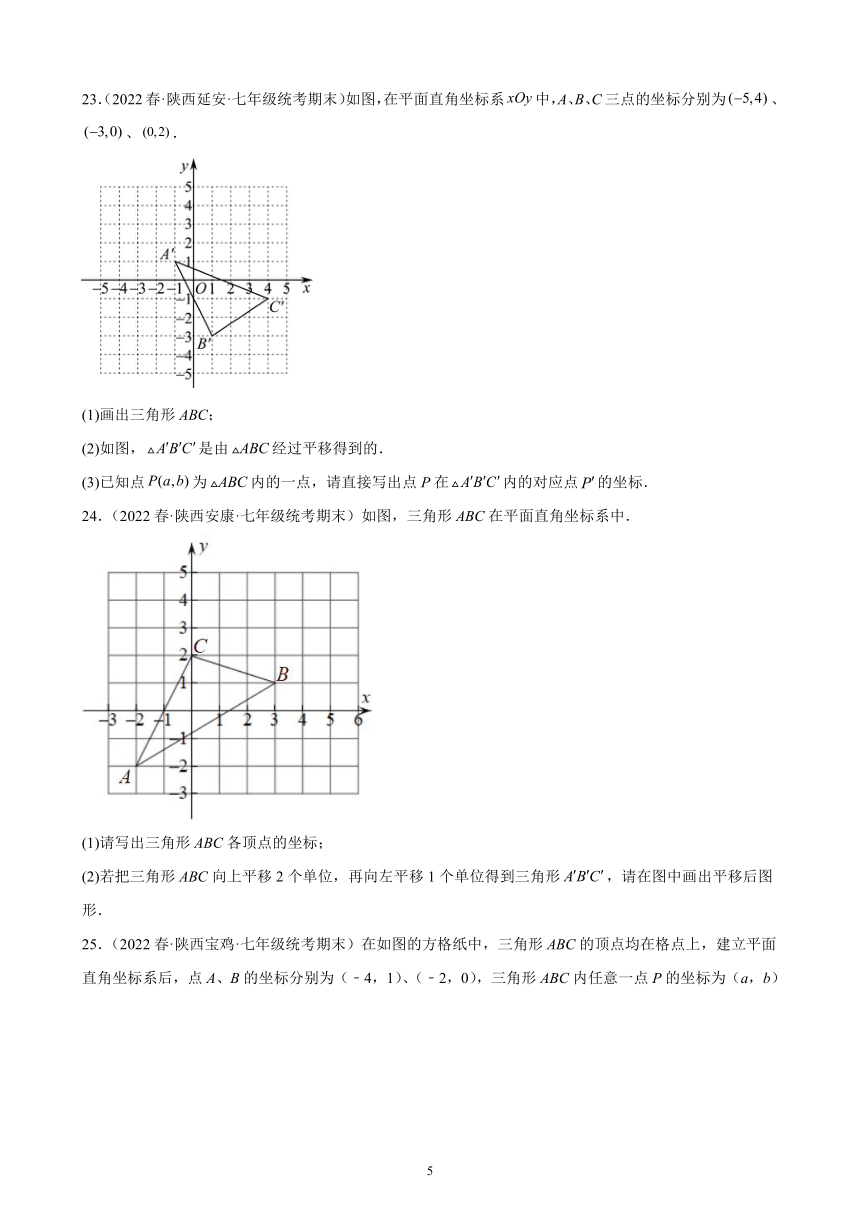
22.(2022春·陕西渭南·七年级统考期末)如图,是一个简单的平面示意图,已知,,,点为的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西方向处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
23.(2022春·陕西延安·七年级统考期末)如图,在平面直角坐标系中,A、B、C三点的坐标分别为、、.
(1)画出三角形ABC;
(2)如图,是由经过平移得到的.
(3)已知点为内的一点,请直接写出点P在内的对应点的坐标.
24.(2022春·陕西安康·七年级统考期末)如图,三角形ABC在平面直角坐标系中.
(1)请写出三角形ABC各顶点的坐标;
(2)若把三角形ABC向上平移2个单位,再向左平移1个单位得到三角形,请在图中画出平移后图形.
25.(2022春·陕西宝鸡·七年级统考期末)在如图的方格纸中,三角形ABC的顶点均在格点上,建立平面直角坐标系后,点A、B的坐标分别为(﹣4,1)、(﹣2,0),三角形ABC内任意一点P的坐标为(a,b)
(1)三角形ABC向右平移 个单位长度到△A1B1C1位置,点C对应点C1的坐标为( ):点P对应点P1的坐标为( )(用含a、b的代数式表示);
(2)三角形ABC经平移后点P的对应点为P2(a+3,b﹣4),请画出上述平移后的三角形A2B2C2,并写出点A2、B2的坐标.
参考答案:
1.B
【分析】根据x轴上点的纵坐标为0可知m+1=0,解出m的值,将m的值代入点P的横坐标即可.
【详解】解:∵点P在x轴上,
∴m+1=0,
解得:m=-1,
把m=-1代入m+3得:-1+3=2,
∴P(2,0),
故选:B
【点睛】本题主要考查了坐标轴上点的坐标特征,掌握“x轴上的点纵坐标为0,y轴上的点横坐标为0”是解题的关键.
2.A
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在第二象限,且到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标是-2,纵坐标是1,
∴点P的坐标为(-2,1).
故选:A.
【点睛】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.
3.D
【分析】根据各象限内点的坐标特征解答即可.
【详解】解:∵横坐标为正,纵坐标为负,
∴点P(2,﹣3)在第四象限,
故选:D.
【点睛】本题考查的是点的坐标与象限的关系,熟记各象限内点的坐标特征是解答本题的关键.
4.D
【分析】直接利用各象限内点的坐标特点分析得出答案.
【详解】解:∵点M的坐标为(x,y),且点M在第二象限,
∴,
∴,
∴点N(-x,-y)在第四象限,
故选:D.
【点睛】本题主要考查平面直角坐标系中点的坐标特点,解决本题的关键是准确掌握平面直角坐标系中各个象限内点的坐标的特点.
5.A
【分析】根据在y轴上的点横坐标为0即可求得m,从而可求得B点坐标.
【详解】解:∵点在y轴上,
∴,解得,
∴,即为,
故选:A.
【点睛】本题考查坐标轴上点的坐标特征,须记住x轴上的点纵坐标为0,y轴上的点横坐标为0.
6.B
【分析】根据、两点纵坐标相等,可确定与轴平行,即可求解.
【详解】解:∵点的坐标为,点的坐标为,、两点纵坐标都为3,
∴轴,
∴线段上任意一点的坐标可表示为,
故选:B.
【点睛】本题主要考查坐标系中点的特点及平行于x轴的点的特点,理解坐标系中点的特点是解题关键.
7.A
【分析】直接利用已知点坐标得出原点位置,进而建立平面直角坐标系,进而得出藏宝位置.
【详解】解:建立平面直角坐标系,如图所示:
藏宝处应为图中的M点.
故选:A.
【点睛】本题主要考查了坐标确定位置,正确得出原点位置,建立坐标系是解题关键.
8.A
【分析】根据平面直角坐标系中,点上下平移横坐标不变、纵坐标上加下减,点左右平移纵坐标不变、横坐标左减右加,即可确定答案.
【详解】解:∵点A(2,3),B(5,1),在y轴正半轴上,在x轴上,
∴线段AB向左平移2个单位长度,向下平移1个单位长度,
∴的纵坐标为,的横坐标为.
故选:A.
【点睛】本题主要考查了坐标与图形变化—平移,解题关键是理解平面坐标系中点平移的特点.
9.A
【分析】根据点的平移:左减右加,上加下减,逆向推导求解可得.
【详解】解:∵先向左平移2个单位,再向下平移3个单位,
∴点A的坐标为(3-2,1-3),即(1,-2).
故选:A.
【点睛】本题考查了坐标与图形变化-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
10.A
【分析】比较平移前A(-1,2),平移后(1,2)的横坐标、纵坐标,可知平移后横坐标加2,纵坐标加4,由于点A、B的平移规律相同,坐标变化也相同,即可得的坐标.
【详解】解:∵平移前A(-1,2),平移后(1,2)
∴平移方式为向右平移2个单位长度,向上平移4个单位长度,
∵平移前点B的坐标为(1,2),
∴平移后点B的坐标为(1+2,2+4)即(3,6),
故选A.
【点睛】本题主要考查了图形的平移,根据A点平移前后的坐标判断出平移方式是解题的关键.
11.(4,﹣5)
【分析】根据点的坐标的几何意义及第四象限内的点的坐标符号的特点即可得出.
【详解】解:∵点P在第四象限,且点P到x轴和y轴的距离分别为5,4,
∴点P的横坐标是4,纵坐标是﹣5,即点P的坐标为(4,﹣5).
故答案为:(4,﹣5).
【点睛】本题主要考查了点在第四象限时点的坐标的符号,以及横坐标的绝对值就是到y轴的距离,纵坐标的绝对值就是到x轴的距离.
12.(﹣2,1)或(﹣3,﹣1)
【分析】根据题意可知2m+3的绝对值等于1,从而可以得到m的值,进而得到M的坐标.
【详解】解:由题意可得:|2m+3|=1,
解得:m=﹣1或m=﹣2,
当m=﹣1时,点M的坐标为(﹣2,1);
当m=﹣2时,点M的坐标为(﹣3,﹣1);
综上,M的坐标为(﹣2,1)或(﹣3,﹣1).
故答案为:(﹣2,1)或(﹣3,﹣1).
【点睛】本题考查点的坐标,熟练掌握点到y轴的距离就是横坐标的绝对值,到x轴的距离就是纵坐标的绝对值是解题的关键.
13.(674,0)
【分析】该点按6次一循环的规律移动,用2022除以6,再确定商和余数即可.
【详解】解:由题意该点按“上→右→下→下→右→上”的方向每6次一循环移动的规律移动,且每移动一个循环向右移动2个单位长度可得,
2022÷6=337,
∴点P2022的横坐标为2×336+2=674,点P2022的纵坐标是0,
故答案为:(674,0).
【点睛】此题考查了点的坐标方面规律问题的解决能力,关键是能准确理解题意确定出点移动的规律.
14.一
【分析】根据有理数的乘法、有理数的加法,可得a、b的符号,根据第一象限内点的横坐标大于零,纵坐标大于零,可得答案.
【详解】解:∵ab>0,a+b>0,
∴a>0,b>0,
点在第一象限,
故答案为:一.
【点睛】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
15.-1
【分析】点坐标向右平移3个单位,就是横坐标加上3,落在y轴上,就是横坐标为0,据此求出x的值即可.
【详解】解:点向右平移3个单位得,
∵平移后的点落在y轴上,
∴,
解得.
故答案是:-1.
【点睛】本题考查点坐标的平移,y轴上点的坐标特征,解题的关键是掌握点坐标平移的方法.
16.
【分析】直接利用马和炮的位置,得出原点的位置,进而得出答案
【详解】解:如图所示:“兵”所在位置坐标为:
故答案为:
【点睛】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
17.6
【分析】利用平移的性质可判断四边形AEFC和四边形BEFD都为平行四边形,然后由平移过程中扫过的面积=S AEFC+S BEFD,根据平行四边形的面积公式进行计算即可.
【详解】解:∵平移折线AEB,得到折线CFD,
∴四边形AEFC和四边形BEFD都为平行四边形,
∴折线AEB在平移过程中扫过的面积=S AEFC+S BEFD
=AO EF+BO EF
=EF(AO+BO)
=EF AB
=[2-(-1)]×[1-(-1)]
=6.
故答案为:6.
【点睛】本题主要考查了坐标与图形-平移,熟练掌握平移的性质:把一个图形整体沿某一直线移动,得到新图形与原图形的形状和大小完全相同;连接各组对应点的线段平行且相等是解决问题的关键.
18.(1)1
(2)或
【分析】(1)根据轴上点的特征即可求得答案.
(2)根据点的坐标轴的距离性质可联立等量关系即可求得答案.
【详解】(1)解:∵点在x轴上,
∴,
解得:.
(2)解∶∵点P到x轴的距离是到y轴距离的2倍,
∴,
∴或,
解得:或7,
∴P点的坐标为或.
【点睛】此题主要考查了点的坐标,正确掌握平面内点的坐标特点,能够正确分类讨论是解题的关键.
19.(1);
(2);
(3)P点坐标为或.
【分析】(1)根据非负数的性质求出,,则可得出答案;
(2)过点P作,由平行线的性质得出,则可得出结论;
(3)由题意得出点P在距离y轴两个长度单位,且平行于y轴的直线上,如图,过点A和分别作y轴的平行线,交直线于点P,则可得出答案.
【详解】(1)解:∵,
∴,,
∴,,
∴;
(2)解:结论:.
理由:如图,过点P作,
∵,
∴,,
∴,
∴;
(3)解:∵;
∴,
∴,
设三角形的边上的高为h,
∵,
∴,
∴点P在距离y轴两个长度单位,且平行于y轴的直线上,
如图,过点A和分别作y轴的平行线,交直线于点P,图中和均满足题意.
∴P点坐标为或.
【点睛】本题属于三角形综合题,考查了坐标与图形性质:利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系,也考查了平移的性质和平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
20.(1)点A的坐标为(2,5);
(2)点A在第一象限.理由见解析
【分析】(1)根据与y轴平行的直线上任意两点横坐标相等列出方程2a-6=2,求出a,进而得到点A的坐标;
(2)根据a的平方根是±3求出a,得到点A的坐标,即可判断点A所在的象限.
【详解】(1)解:根据题意,可得2a-6=2,
解得a=4,
则a+1=4+1=5,
所以点A的坐标为(2,5);
(2)解:点A在第一象限,理由如下:
∵a的平方根是±3,
∴a=9,
∴2a-6=2×9-6=12,a+1=9+1=10,
∴点A的坐标为(12,10),
∴点A在第一象限.
【点睛】本题考查了坐标与图形性质,平面直角坐标系中点的特点,平方根;熟练掌握平面直角坐标系中与坐标轴平行的直线上点的特点是解题的关键.
21.(1)点A的坐标为
(2)点A的坐标为或
【分析】(1)根据x轴上点的特征进行解答,即可得出答案;
(2)由点A到两坐标轴的距离相等的点横纵坐标绝对值相等列出方程求解即可.
(1)
解:∵点A在x轴上
∴,解得,
∴,
∴点A的坐标为;
(2)
解:∵点A到x轴、y轴的距离相等
∴,解得或2.
当时,,此时点A的坐标为;
当时,,此时点A的坐标为.
故点A的坐标为或.
【点睛】本题主要考查了根据点的特征列出方程求点的坐标,掌握根据点的特征列出方程是解题的关键.
22.(1)学校在小明家北偏东方向处,博物馆在小明家南偏东方向处
(2)小明家距离相同的是学校和公园和影院
【分析】(1)先求出45°的余角,40°的余角,然后再根据方向角的定义即可解答;
(2)根据线段的中点定义可得OE=2km,再结合已知可得OA=OD=OE,即可解答.
【详解】(1)解:由题意得: 90°-45°=45°,90°-40°=50°,
学校在小明家北偏东45°方向2km处,
博物馆在小明家南偏东50°方向4km处;
(2)∵OC=4km,点E为OC的中点,
∴OE=OC=2(km),
∵OB=6km,BD=4km,
∴OD=OB-BD=2(km),
∵OA=2km,
∴OA=OD=OE,
∴图中到小明家距离相同的是影院,公园,学校.
【点睛】本题考查了方向角,位置的表示,熟练掌握方向角的定义是解题的关键.
23.(1)见解析
(2)先向右平移4个单位,再向下平移3个单位
(3)
【分析】(1)根据A,B,C的坐标作出图形即可.
(2)根据平移变换的规律解决问题即可.
(3)利用平移规律解决问题即可.
(1)
解:如图,△ABC即为所求.
S△ABC=4×5-×2×4-×2×5-×2×3=8;
(2)
先向右平移4个单位,再向下平移3个单位.
(3)
由题意可得:P′(a+4,b-3).
【点睛】本题考查坐标与图形的变化-平移,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
24.(1),,
(2)见解析
【分析】(1)根据题意,写出各点的坐标,即可得出答案.
(2)根据平移的性质,得到,即可求解.
(1)
解:根据题意得:,,;
(2)
解:∵三角形ABC向上平移2个单位,再向左平移1个单位得到三角形,,,,
∴点,
三角形即为所求,如图.
【点睛】本题考查坐标与图形变换——平移,熟练掌握平移的性质是解答本题的关键.
25.(1)5、(2,3)、(a+5,b);(2)图见解析,A2(﹣1,-3),B2(1,﹣4)
【分析】(1)根据坐标系可得答案;
(2)根据点P平移后的对应点位置可得图形向右平移3个单位,向下平移4个单位,然后再确定A、B、C三点平移后的对应点位置,再连接即可.
【详解】解:(1)三角形ABC向右平移5个单位长度到△A1B1C1位置,点C对应点C1的坐标为(2,3):点P对应点P1的坐标为(a+5,b),
故答案为:5;(2,3);(a+5,b);
(2)如图所示:A2(﹣1,-3),B2(1,﹣4).
【点睛】本题考查了网格图中图形的平移,熟练掌握平移的要点是解题的关键.
一、单选题
1.(2022春·陕西渭南·七年级统考期末)若点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
2.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,若点P在第二象限,且点P到x轴的距离为1,到y轴的距离为2,则点P的坐标为( )
A. B. C. D.
3.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,第二象限内点的坐标为,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·陕西渭南·七年级统考期末)在平面直角坐标系中,若点在y轴上,则点的坐标为( )
A.(3,-3) B.(5,-1) C.(3,3) D.(5,1)
6.(2022春·陕西商洛·七年级校考期末)在平面直角坐标系中,点的坐标为,点的坐标为,则线段上任意一点的坐标可表示为( )
A. B.
C. D.
7.(2022春·陕西渭南·七年级统考期末)在一次“寻宝”游戏中,寻宝人已经找到两个标志点和,并且知道藏宝地点的坐标是,则藏宝处应为图中的( )
A.点 B.点 C.点 D.点
8.(2022春·陕西延安·七年级统考期末)如图,已知点A(2,3),B(5,1),若将线段AB平移至A1B1, A1在y轴正半轴上,B1在x轴上,则A1的纵坐标、B1的横坐标分别为( )
A.2,3 B.1,4 C.2,2 D.1,3
9.(2022春·陕西渭南·七年级统考期末)在平面直角坐标系中,将点先向左平移2个单位,再向下平移3个单位,则移动后得到的点的坐标是( )
A. B. C. D.
10.(2022春·陕西商洛·七年级统考期末)已知线段的端点,,将线段平移后,点坐标是,则点的坐标是( )
A. B. C. D.
二、填空题
11.(2022春·陕西宝鸡·七年级统考期末)在平面直角坐标系xOy中,若点P在第四象限,且点P到x轴和y轴距离分别为5和4,则点P的坐标为________________.
12.(2022春·陕西安康·七年级统考期末)已知平面直角坐标系中有一点M(m﹣1,2m+3),若点M到x轴的距离为1,则点M的坐标为_____.
13.(2022春·陕西安康·七年级统考期末)如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是______.
14.(2022春·陕西渭南·七年级统考期末)已知点,,,则点在第__________象限.
15.(2022春·陕西安康·七年级统考期末)将点向右平移3个单位后,落在轴上,则的值为______.
16.(2022春·陕西渭南·七年级统考期末)中华象棋文化博大精深,渊源深厚,如图所示,在象棋盘上建立平面直角坐标系,是“马”位于点,“炮”位于,写出“兵”所在位置的坐标_______.
17.(2022春·陕西渭南·七年级统考期末)如图,在平面直角坐标系中,将折线向右平移得到折线,则折线在平移过程中扫过的面积是______.
三、解答题
18.(2022春·陕西宝鸡·七年级统考期末)已知点.
(1)若点P在x轴上,求m的值;
(2)若点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
19.(2022春·陕西商洛·七年级校考期末)如图1,在平面直角坐标系中,点A,B的坐标分别是.且a、b满足现同时将点A,B分别向上平移3个单位长度,再向右平移2个单位长度,得到A,B的对应点D,C,连接,,.
(1)写出点A,B的坐标.
(2)如图2,当点P在线段上时,连接,,请求出与, 的数量关系.
(3)如图3,当点P在直线上时,若,通过观察图形直接写出点P的坐标.
20.(2022春·陕西安康·七年级统考期末)已知点.
(1)点A与点的连线与轴平行,求点A的坐标.
(2)若的平方根是,试判断点A所在的象限,并说明理由.
21.(2022春·陕西安康·七年级统考期末)在平面直角坐标系中,已知点.
(1)若点A在x轴上,求点A的坐标;
(2)若点A到x轴、y轴的距离相等,求点A的坐标.
22.(2022春·陕西渭南·七年级统考期末)如图,是一个简单的平面示意图,已知,,,点为的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西方向处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
23.(2022春·陕西延安·七年级统考期末)如图,在平面直角坐标系中,A、B、C三点的坐标分别为、、.
(1)画出三角形ABC;
(2)如图,是由经过平移得到的.
(3)已知点为内的一点,请直接写出点P在内的对应点的坐标.
24.(2022春·陕西安康·七年级统考期末)如图,三角形ABC在平面直角坐标系中.
(1)请写出三角形ABC各顶点的坐标;
(2)若把三角形ABC向上平移2个单位,再向左平移1个单位得到三角形,请在图中画出平移后图形.
25.(2022春·陕西宝鸡·七年级统考期末)在如图的方格纸中,三角形ABC的顶点均在格点上,建立平面直角坐标系后,点A、B的坐标分别为(﹣4,1)、(﹣2,0),三角形ABC内任意一点P的坐标为(a,b)
(1)三角形ABC向右平移 个单位长度到△A1B1C1位置,点C对应点C1的坐标为( ):点P对应点P1的坐标为( )(用含a、b的代数式表示);
(2)三角形ABC经平移后点P的对应点为P2(a+3,b﹣4),请画出上述平移后的三角形A2B2C2,并写出点A2、B2的坐标.
参考答案:
1.B
【分析】根据x轴上点的纵坐标为0可知m+1=0,解出m的值,将m的值代入点P的横坐标即可.
【详解】解:∵点P在x轴上,
∴m+1=0,
解得:m=-1,
把m=-1代入m+3得:-1+3=2,
∴P(2,0),
故选:B
【点睛】本题主要考查了坐标轴上点的坐标特征,掌握“x轴上的点纵坐标为0,y轴上的点横坐标为0”是解题的关键.
2.A
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在第二象限,且到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标是-2,纵坐标是1,
∴点P的坐标为(-2,1).
故选:A.
【点睛】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.
3.D
【分析】根据各象限内点的坐标特征解答即可.
【详解】解:∵横坐标为正,纵坐标为负,
∴点P(2,﹣3)在第四象限,
故选:D.
【点睛】本题考查的是点的坐标与象限的关系,熟记各象限内点的坐标特征是解答本题的关键.
4.D
【分析】直接利用各象限内点的坐标特点分析得出答案.
【详解】解:∵点M的坐标为(x,y),且点M在第二象限,
∴,
∴,
∴点N(-x,-y)在第四象限,
故选:D.
【点睛】本题主要考查平面直角坐标系中点的坐标特点,解决本题的关键是准确掌握平面直角坐标系中各个象限内点的坐标的特点.
5.A
【分析】根据在y轴上的点横坐标为0即可求得m,从而可求得B点坐标.
【详解】解:∵点在y轴上,
∴,解得,
∴,即为,
故选:A.
【点睛】本题考查坐标轴上点的坐标特征,须记住x轴上的点纵坐标为0,y轴上的点横坐标为0.
6.B
【分析】根据、两点纵坐标相等,可确定与轴平行,即可求解.
【详解】解:∵点的坐标为,点的坐标为,、两点纵坐标都为3,
∴轴,
∴线段上任意一点的坐标可表示为,
故选:B.
【点睛】本题主要考查坐标系中点的特点及平行于x轴的点的特点,理解坐标系中点的特点是解题关键.
7.A
【分析】直接利用已知点坐标得出原点位置,进而建立平面直角坐标系,进而得出藏宝位置.
【详解】解:建立平面直角坐标系,如图所示:
藏宝处应为图中的M点.
故选:A.
【点睛】本题主要考查了坐标确定位置,正确得出原点位置,建立坐标系是解题关键.
8.A
【分析】根据平面直角坐标系中,点上下平移横坐标不变、纵坐标上加下减,点左右平移纵坐标不变、横坐标左减右加,即可确定答案.
【详解】解:∵点A(2,3),B(5,1),在y轴正半轴上,在x轴上,
∴线段AB向左平移2个单位长度,向下平移1个单位长度,
∴的纵坐标为,的横坐标为.
故选:A.
【点睛】本题主要考查了坐标与图形变化—平移,解题关键是理解平面坐标系中点平移的特点.
9.A
【分析】根据点的平移:左减右加,上加下减,逆向推导求解可得.
【详解】解:∵先向左平移2个单位,再向下平移3个单位,
∴点A的坐标为(3-2,1-3),即(1,-2).
故选:A.
【点睛】本题考查了坐标与图形变化-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
10.A
【分析】比较平移前A(-1,2),平移后(1,2)的横坐标、纵坐标,可知平移后横坐标加2,纵坐标加4,由于点A、B的平移规律相同,坐标变化也相同,即可得的坐标.
【详解】解:∵平移前A(-1,2),平移后(1,2)
∴平移方式为向右平移2个单位长度,向上平移4个单位长度,
∵平移前点B的坐标为(1,2),
∴平移后点B的坐标为(1+2,2+4)即(3,6),
故选A.
【点睛】本题主要考查了图形的平移,根据A点平移前后的坐标判断出平移方式是解题的关键.
11.(4,﹣5)
【分析】根据点的坐标的几何意义及第四象限内的点的坐标符号的特点即可得出.
【详解】解:∵点P在第四象限,且点P到x轴和y轴的距离分别为5,4,
∴点P的横坐标是4,纵坐标是﹣5,即点P的坐标为(4,﹣5).
故答案为:(4,﹣5).
【点睛】本题主要考查了点在第四象限时点的坐标的符号,以及横坐标的绝对值就是到y轴的距离,纵坐标的绝对值就是到x轴的距离.
12.(﹣2,1)或(﹣3,﹣1)
【分析】根据题意可知2m+3的绝对值等于1,从而可以得到m的值,进而得到M的坐标.
【详解】解:由题意可得:|2m+3|=1,
解得:m=﹣1或m=﹣2,
当m=﹣1时,点M的坐标为(﹣2,1);
当m=﹣2时,点M的坐标为(﹣3,﹣1);
综上,M的坐标为(﹣2,1)或(﹣3,﹣1).
故答案为:(﹣2,1)或(﹣3,﹣1).
【点睛】本题考查点的坐标,熟练掌握点到y轴的距离就是横坐标的绝对值,到x轴的距离就是纵坐标的绝对值是解题的关键.
13.(674,0)
【分析】该点按6次一循环的规律移动,用2022除以6,再确定商和余数即可.
【详解】解:由题意该点按“上→右→下→下→右→上”的方向每6次一循环移动的规律移动,且每移动一个循环向右移动2个单位长度可得,
2022÷6=337,
∴点P2022的横坐标为2×336+2=674,点P2022的纵坐标是0,
故答案为:(674,0).
【点睛】此题考查了点的坐标方面规律问题的解决能力,关键是能准确理解题意确定出点移动的规律.
14.一
【分析】根据有理数的乘法、有理数的加法,可得a、b的符号,根据第一象限内点的横坐标大于零,纵坐标大于零,可得答案.
【详解】解:∵ab>0,a+b>0,
∴a>0,b>0,
点在第一象限,
故答案为:一.
【点睛】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
15.-1
【分析】点坐标向右平移3个单位,就是横坐标加上3,落在y轴上,就是横坐标为0,据此求出x的值即可.
【详解】解:点向右平移3个单位得,
∵平移后的点落在y轴上,
∴,
解得.
故答案是:-1.
【点睛】本题考查点坐标的平移,y轴上点的坐标特征,解题的关键是掌握点坐标平移的方法.
16.
【分析】直接利用马和炮的位置,得出原点的位置,进而得出答案
【详解】解:如图所示:“兵”所在位置坐标为:
故答案为:
【点睛】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
17.6
【分析】利用平移的性质可判断四边形AEFC和四边形BEFD都为平行四边形,然后由平移过程中扫过的面积=S AEFC+S BEFD,根据平行四边形的面积公式进行计算即可.
【详解】解:∵平移折线AEB,得到折线CFD,
∴四边形AEFC和四边形BEFD都为平行四边形,
∴折线AEB在平移过程中扫过的面积=S AEFC+S BEFD
=AO EF+BO EF
=EF(AO+BO)
=EF AB
=[2-(-1)]×[1-(-1)]
=6.
故答案为:6.
【点睛】本题主要考查了坐标与图形-平移,熟练掌握平移的性质:把一个图形整体沿某一直线移动,得到新图形与原图形的形状和大小完全相同;连接各组对应点的线段平行且相等是解决问题的关键.
18.(1)1
(2)或
【分析】(1)根据轴上点的特征即可求得答案.
(2)根据点的坐标轴的距离性质可联立等量关系即可求得答案.
【详解】(1)解:∵点在x轴上,
∴,
解得:.
(2)解∶∵点P到x轴的距离是到y轴距离的2倍,
∴,
∴或,
解得:或7,
∴P点的坐标为或.
【点睛】此题主要考查了点的坐标,正确掌握平面内点的坐标特点,能够正确分类讨论是解题的关键.
19.(1);
(2);
(3)P点坐标为或.
【分析】(1)根据非负数的性质求出,,则可得出答案;
(2)过点P作,由平行线的性质得出,则可得出结论;
(3)由题意得出点P在距离y轴两个长度单位,且平行于y轴的直线上,如图,过点A和分别作y轴的平行线,交直线于点P,则可得出答案.
【详解】(1)解:∵,
∴,,
∴,,
∴;
(2)解:结论:.
理由:如图,过点P作,
∵,
∴,,
∴,
∴;
(3)解:∵;
∴,
∴,
设三角形的边上的高为h,
∵,
∴,
∴点P在距离y轴两个长度单位,且平行于y轴的直线上,
如图,过点A和分别作y轴的平行线,交直线于点P,图中和均满足题意.
∴P点坐标为或.
【点睛】本题属于三角形综合题,考查了坐标与图形性质:利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系,也考查了平移的性质和平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
20.(1)点A的坐标为(2,5);
(2)点A在第一象限.理由见解析
【分析】(1)根据与y轴平行的直线上任意两点横坐标相等列出方程2a-6=2,求出a,进而得到点A的坐标;
(2)根据a的平方根是±3求出a,得到点A的坐标,即可判断点A所在的象限.
【详解】(1)解:根据题意,可得2a-6=2,
解得a=4,
则a+1=4+1=5,
所以点A的坐标为(2,5);
(2)解:点A在第一象限,理由如下:
∵a的平方根是±3,
∴a=9,
∴2a-6=2×9-6=12,a+1=9+1=10,
∴点A的坐标为(12,10),
∴点A在第一象限.
【点睛】本题考查了坐标与图形性质,平面直角坐标系中点的特点,平方根;熟练掌握平面直角坐标系中与坐标轴平行的直线上点的特点是解题的关键.
21.(1)点A的坐标为
(2)点A的坐标为或
【分析】(1)根据x轴上点的特征进行解答,即可得出答案;
(2)由点A到两坐标轴的距离相等的点横纵坐标绝对值相等列出方程求解即可.
(1)
解:∵点A在x轴上
∴,解得,
∴,
∴点A的坐标为;
(2)
解:∵点A到x轴、y轴的距离相等
∴,解得或2.
当时,,此时点A的坐标为;
当时,,此时点A的坐标为.
故点A的坐标为或.
【点睛】本题主要考查了根据点的特征列出方程求点的坐标,掌握根据点的特征列出方程是解题的关键.
22.(1)学校在小明家北偏东方向处,博物馆在小明家南偏东方向处
(2)小明家距离相同的是学校和公园和影院
【分析】(1)先求出45°的余角,40°的余角,然后再根据方向角的定义即可解答;
(2)根据线段的中点定义可得OE=2km,再结合已知可得OA=OD=OE,即可解答.
【详解】(1)解:由题意得: 90°-45°=45°,90°-40°=50°,
学校在小明家北偏东45°方向2km处,
博物馆在小明家南偏东50°方向4km处;
(2)∵OC=4km,点E为OC的中点,
∴OE=OC=2(km),
∵OB=6km,BD=4km,
∴OD=OB-BD=2(km),
∵OA=2km,
∴OA=OD=OE,
∴图中到小明家距离相同的是影院,公园,学校.
【点睛】本题考查了方向角,位置的表示,熟练掌握方向角的定义是解题的关键.
23.(1)见解析
(2)先向右平移4个单位,再向下平移3个单位
(3)
【分析】(1)根据A,B,C的坐标作出图形即可.
(2)根据平移变换的规律解决问题即可.
(3)利用平移规律解决问题即可.
(1)
解:如图,△ABC即为所求.
S△ABC=4×5-×2×4-×2×5-×2×3=8;
(2)
先向右平移4个单位,再向下平移3个单位.
(3)
由题意可得:P′(a+4,b-3).
【点睛】本题考查坐标与图形的变化-平移,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
24.(1),,
(2)见解析
【分析】(1)根据题意,写出各点的坐标,即可得出答案.
(2)根据平移的性质,得到,即可求解.
(1)
解:根据题意得:,,;
(2)
解:∵三角形ABC向上平移2个单位,再向左平移1个单位得到三角形,,,,
∴点,
三角形即为所求,如图.
【点睛】本题考查坐标与图形变换——平移,熟练掌握平移的性质是解答本题的关键.
25.(1)5、(2,3)、(a+5,b);(2)图见解析,A2(﹣1,-3),B2(1,﹣4)
【分析】(1)根据坐标系可得答案;
(2)根据点P平移后的对应点位置可得图形向右平移3个单位,向下平移4个单位,然后再确定A、B、C三点平移后的对应点位置,再连接即可.
【详解】解:(1)三角形ABC向右平移5个单位长度到△A1B1C1位置,点C对应点C1的坐标为(2,3):点P对应点P1的坐标为(a+5,b),
故答案为:5;(2,3);(a+5,b);
(2)如图所示:A2(﹣1,-3),B2(1,﹣4).
【点睛】本题考查了网格图中图形的平移,熟练掌握平移的要点是解题的关键.
