有理数加法法则[上学期]

课件16张PPT。2.6 有理数加法 小明沿着西坞中学门口的一条东西向的路，先走了20米，又走了30米，能否确定他现在位于原来位置的哪个方向，相距多少米?（现规定向东为正，向西为负 ） 两次运动的可能情形：?
（1）两次向相同方向运动（2）两次向相反方向运动两次都向东两次都向西先向东，再向西先向西，再向东返回5两次都向东走在数轴上的表示(1)两次都向西走，一共向东走了50米，
算式： (+20)+(+30)= +50，
?
东
+西—(2) 两次都向西走，一共向西走了50米，
算式?： (-20)+(-30)= -50.
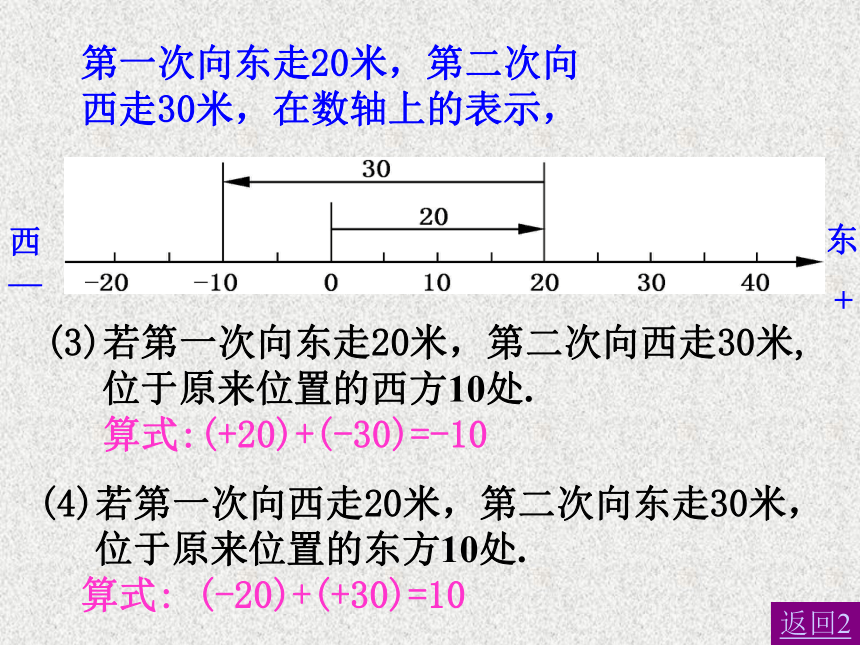
返回2第一次向东走20米，第二次向西走30米，在数轴上的表示，
(3)若第一次向东走20米，第二次向西走30米,
位于原来位置的西方10处.
算式:(+20)+(-30)=-10东
+(4)若第一次向西走20米，第二次向东走30米，
位于原来位置的东方10处.
算式: (-20)+(+30)=10返回2西
—下式中的加数不仿仍可看作运动的方向和路程：
(+4)+(-3)=( )
? (+3)+(-10)=( )
(-5)+(+7)=( )
? (-6)+ 2 = ( )
试一试1-72-4(5)第一次向西走了30米，
第二次向东走了30米.
算式：(-30)+(+30)=( ).
?
(6)第一次向西走了30米，第二次没走.
算式：(-30)+ 0 =( ).
两种特殊情形：0-30(+20)+(+30)=+50
(-20)+(-30)=-50
你能发现和与两个加数的符号和绝对值之间有什么关系吗? (+20)+(-30)=-10
(-20)+(+30)=10
(+4)+(-3)= 1
(+3)+(-10)= -7
(-5)+(+7)= 2
(-6)+ 2 = -4
有理数加法法则：
1. 同号两数相加，取相同的符 号，并把绝对值相加；
2. 绝对值不等的异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值；
3. 互为相反数的两个数相加得0；
4. 一个数同0相加，仍得这个数 (-30)+(+30)=0
(-30)+ 0 =-30 同号两数相加，取相同的符号，
并把绝对值相加；
?
2. 绝对值不等的异号两数相加，
取绝对值较大加数的符号，
并用较大的绝对值减去较小的绝对值；
?
3. 互为相反数的两个数相加得0；
?4. 一个数同0相加，仍得这个数.
有理数的加法法则练习1: 填 表+ 18+8 26+ 16-9 7- 9+5 -14 例1 计算：
(1)(+2)+(-11);
(2)(+20)+(+12);
(4)(-3.4)+4.3(3)解: (1)(+2)+(-11)=-(11-2)=-9(2)(+20)+(+12)=+(20+12)=+32=32; (4)(-3.4)+4.3=+(4.3-3.4)=0.9
(3)练习2. 计算：
(1)10+(-4);
(2)(+9)+7;
(3)(-15)+(-32);
(4)(-9)+0;
(5)100+(-199);
(6)(-0.5)+4.4;
+(1.25) 有理数的加法法则：
?1.同号两数相加，取相同的符 号，并把绝对值相加；
?2.绝对值不等的异号两数相加，取绝对值较大加数的符号，并用较大的绝对值减去较小的绝对值
?3.互为相反数的两个数相加得0
?4.一个数同0相加，仍得这个数.
(7)(8)答案：
(1)6, (2)16, (3)-47,


(4)-9, (5)-99, (6)3.9,
(7)0, (8)
练习3. 填 空：
(1)( )+(-3)=-8；

(2)( )+(-3)= 8；

(3)(-3)+( )=-1；
(4)(-3)+( )= 0 .
-51123两个有理数相加，和是否一定大于每个加数？想一想怎样的两个有理数相加，和一定大于每个加数？两个正数（1）通过两次运动总结果的不同，得出有理数加法法则，观察加数的符号与和的符号，加数的绝对值与和的绝对值，运用有理数加法法则，进行有理数加法运算。（2）有理数加法运算法则，主要掌握两个环节：“同号还是异号”与“绝对值”。首先判断两个加数符号是同号？是异号？或者是有一个零，来确定用哪条法则。小结 链接生活
（生活中有很多问题可以用有理数加法来解决）（1）存折中有550元，取出300元，又存入170元后，存折中还有多少钱？（2）某仓库一天的进出库情况如下：进库记为正，出库记为负，已知原有库存为300，请计算仓库这一天的库存为多少？+13，-1，+15，-12，+8，-10，+4，-15，+14，-16。算式：
300+(+13)+(-1)+(+15)+(-12)+(+8)+(-10)+(+4)+(-15)+(+14)+(-16)
=300 算式：记存入为正,取出为负,
550+(-300)+170=420
, 祝同学们今后在数学广阔的天空中更加自由的翱翔！