4.2图形的全等 强化训练卷(含答案)数学北师大版七年级下册
文档属性
| 名称 | 4.2图形的全等 强化训练卷(含答案)数学北师大版七年级下册 |
|
|
| 格式 | zip | ||
| 文件大小 | 345.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 20:01:29 | ||
图片预览

文档简介
4.2图形的全等 强化训练卷
一、单选题
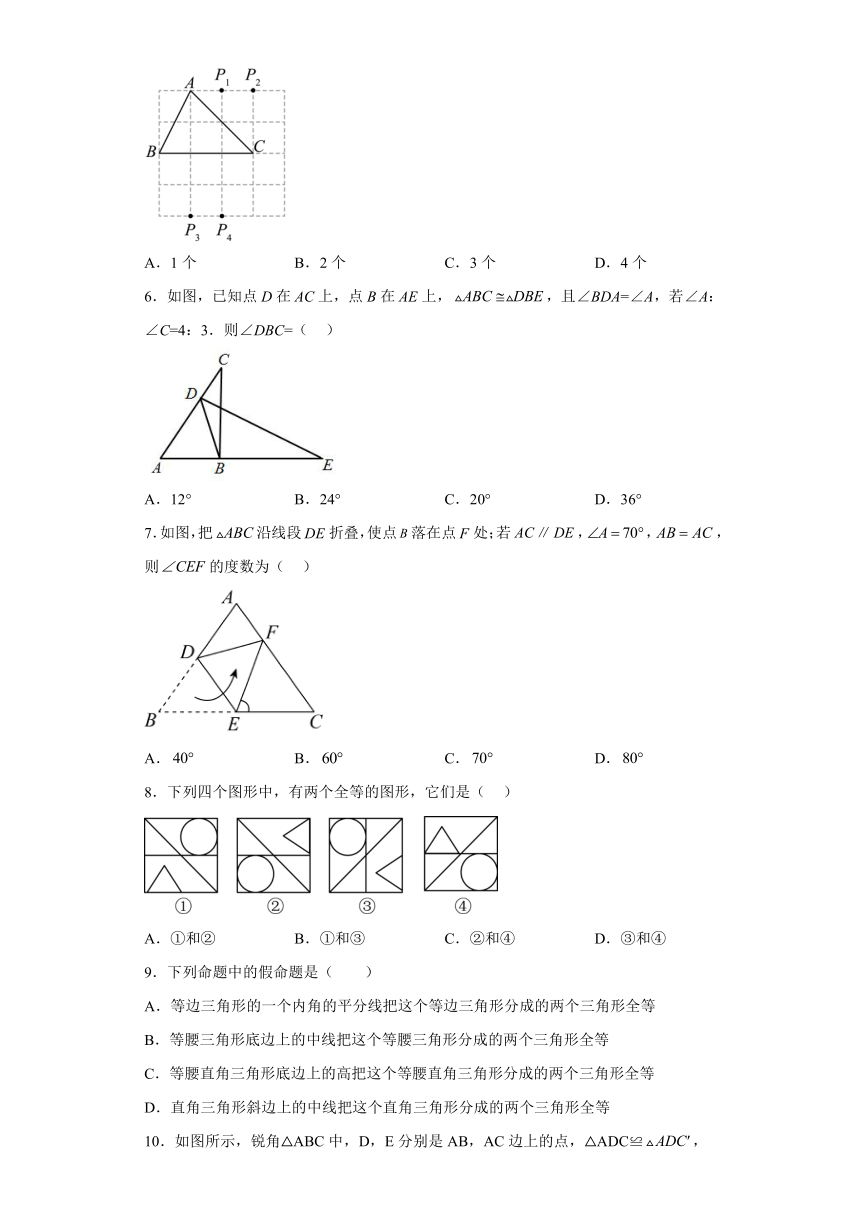
1.如图,两个三角形△ABC与△BDE全等,观察图形,判断在这两个三角形中边DE的对应边为( )
A.BE B.AB C.CA D.BC
2.一定是全等三角形的是( )
A.面积相等的三角形
B.周长相等的三角形
C.形状相同的三角形
D.能够完全重合的两个三角形
3.下列说法正确的是
A.全等三角形是指形状相同的两个三角形 B.全等三角形是指面积相等的两个三角形 C.两个等边三角形是全等三角形 D.全等三角形是指两个能完全重合的三角形
4.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
5.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△的顶点都在格点上,以为一边作△BC,使之与△全等,从、、、四点中找出符合条件的点,则点有( )
A.1个 B.2个 C.3个 D.4个
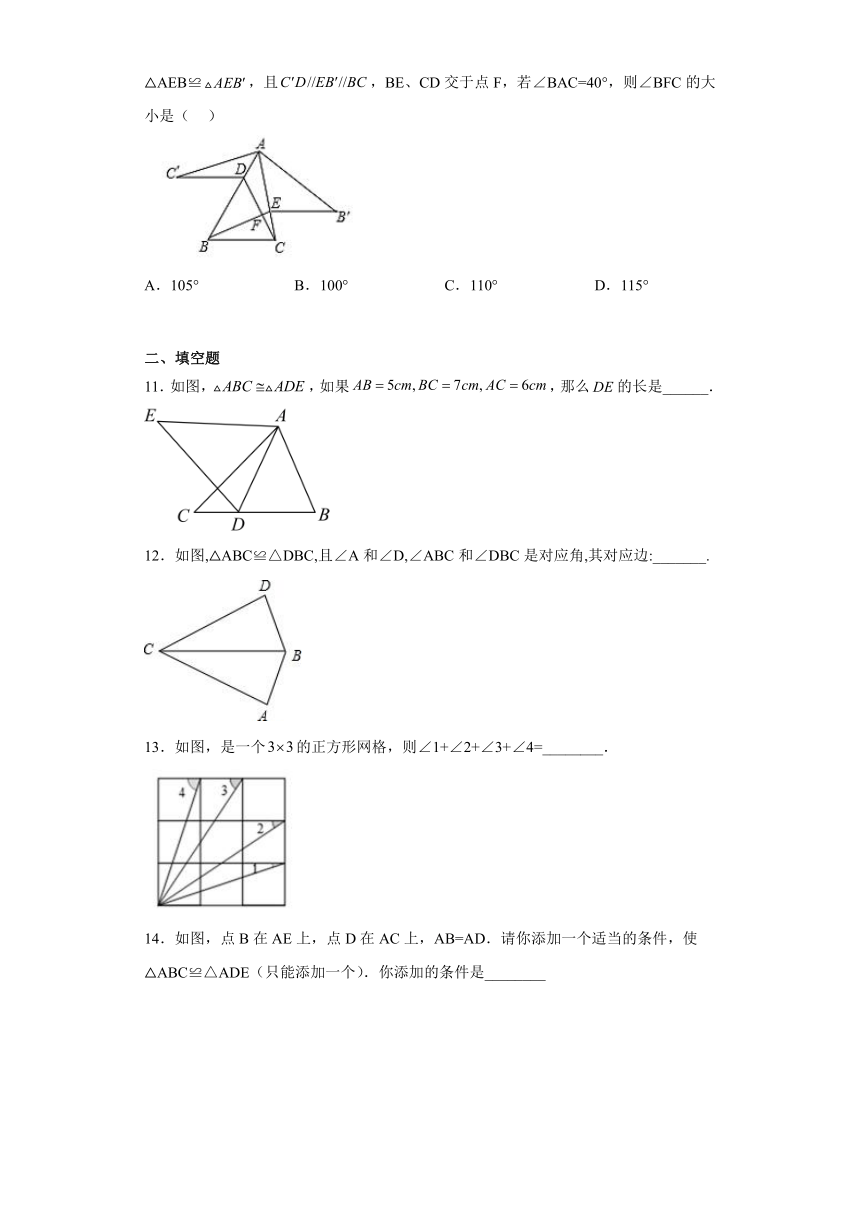
6.如图,已知点D在AC上,点B在AE上,,且∠BDA=∠A,若∠A:∠C=4:3.则∠DBC=( )
A.12° B.24° C.20° D.36°
7.如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
8.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③ C.②和④ D.③和④
9.下列命题中的假命题是( )
A.等边三角形的一个内角的平分线把这个等边三角形分成的两个三角形全等
B.等腰三角形底边上的中线把这个等腰三角形分成的两个三角形全等
C.等腰直角三角形底边上的高把这个等腰直角三角形分成的两个三角形全等
D.直角三角形斜边上的中线把这个直角三角形分成的两个三角形全等
10.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌,△AEB≌,且,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
二、填空题
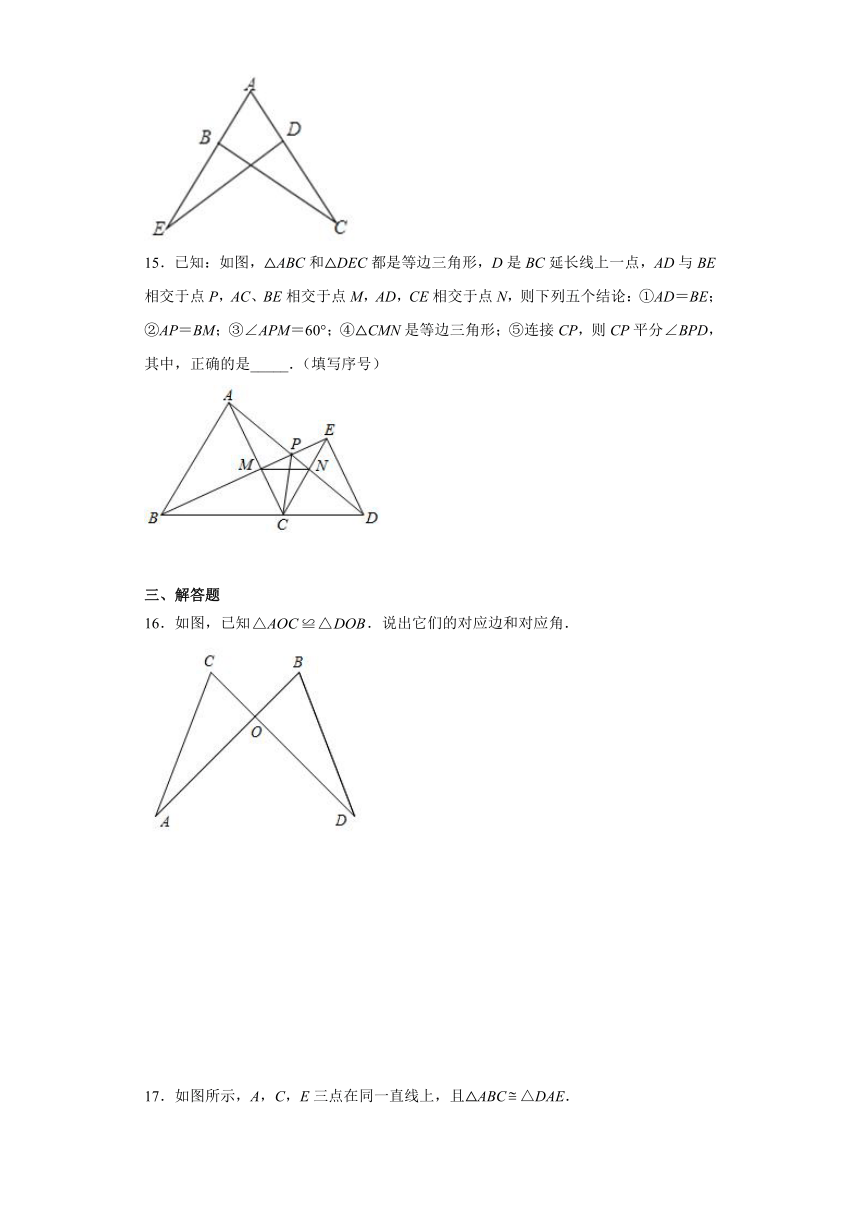
11.如图,,如果,那么的长是______.
12.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边:_______.
13.如图,是一个的正方形网格,则∠1+∠2+∠3+∠4=________.
14.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是________
15.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)
三、解答题
16.如图,已知.说出它们的对应边和对应角.
17.如图所示,A,C,E三点在同一直线上,且△ABC△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BCDE?请说明理由.
18.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
19.如图,已知,点,,,在同一条直线上.
(1)若,,求的度数;
(2)若,,求的长.
20.将一个正方形剖成4个全等的部分.
参考答案
1.B
2.D
3.D
4.B
5.C
6.A
7.C
8.B
9.D
10.B
11.
12.BC和BC,CD和CA,BD和AB
13.180°.
14.AE=AC
15.①③④⑤.
16.解:∵,
∴的对应边是,的对应边是,的对应边是,的对应角是,的对应角是,的对应角是.
17.(1)证明:∵△ABC△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BCDE,
∴∠BCE=∠E,
又∵△ABC△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BCDE.
18.解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
19.(1)解:∵,,
∴,
∵,
∴;
(2)解∵,
∴,
∵,
∴,
∴.
20.
或均可,答案不唯一
一、单选题
1.如图,两个三角形△ABC与△BDE全等,观察图形,判断在这两个三角形中边DE的对应边为( )
A.BE B.AB C.CA D.BC
2.一定是全等三角形的是( )
A.面积相等的三角形
B.周长相等的三角形
C.形状相同的三角形
D.能够完全重合的两个三角形
3.下列说法正确的是
A.全等三角形是指形状相同的两个三角形 B.全等三角形是指面积相等的两个三角形 C.两个等边三角形是全等三角形 D.全等三角形是指两个能完全重合的三角形
4.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
5.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△的顶点都在格点上,以为一边作△BC,使之与△全等,从、、、四点中找出符合条件的点,则点有( )
A.1个 B.2个 C.3个 D.4个
6.如图,已知点D在AC上,点B在AE上,,且∠BDA=∠A,若∠A:∠C=4:3.则∠DBC=( )
A.12° B.24° C.20° D.36°
7.如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
8.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③ C.②和④ D.③和④
9.下列命题中的假命题是( )
A.等边三角形的一个内角的平分线把这个等边三角形分成的两个三角形全等
B.等腰三角形底边上的中线把这个等腰三角形分成的两个三角形全等
C.等腰直角三角形底边上的高把这个等腰直角三角形分成的两个三角形全等
D.直角三角形斜边上的中线把这个直角三角形分成的两个三角形全等
10.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌,△AEB≌,且,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105° B.100° C.110° D.115°
二、填空题
11.如图,,如果,那么的长是______.
12.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边:_______.
13.如图,是一个的正方形网格,则∠1+∠2+∠3+∠4=________.
14.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是________
15.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)
三、解答题
16.如图,已知.说出它们的对应边和对应角.
17.如图所示,A,C,E三点在同一直线上,且△ABC△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BCDE?请说明理由.
18.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
19.如图,已知,点,,,在同一条直线上.
(1)若,,求的度数;
(2)若,,求的长.
20.将一个正方形剖成4个全等的部分.
参考答案
1.B
2.D
3.D
4.B
5.C
6.A
7.C
8.B
9.D
10.B
11.
12.BC和BC,CD和CA,BD和AB
13.180°.
14.AE=AC
15.①③④⑤.
16.解:∵,
∴的对应边是,的对应边是,的对应边是,的对应角是,的对应角是,的对应角是.
17.(1)证明:∵△ABC△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BCDE,
∴∠BCE=∠E,
又∵△ABC△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BCDE.
18.解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
19.(1)解:∵,,
∴,
∵,
∴;
(2)解∵,
∴,
∵,
∴,
∴.
20.
或均可,答案不唯一
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
