第三单元比例—正比例导学案 六年级数学下册-青岛版(有答案)
文档属性
| 名称 | 第三单元比例—正比例导学案 六年级数学下册-青岛版(有答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 376.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 22:10:41 | ||
图片预览

文档简介
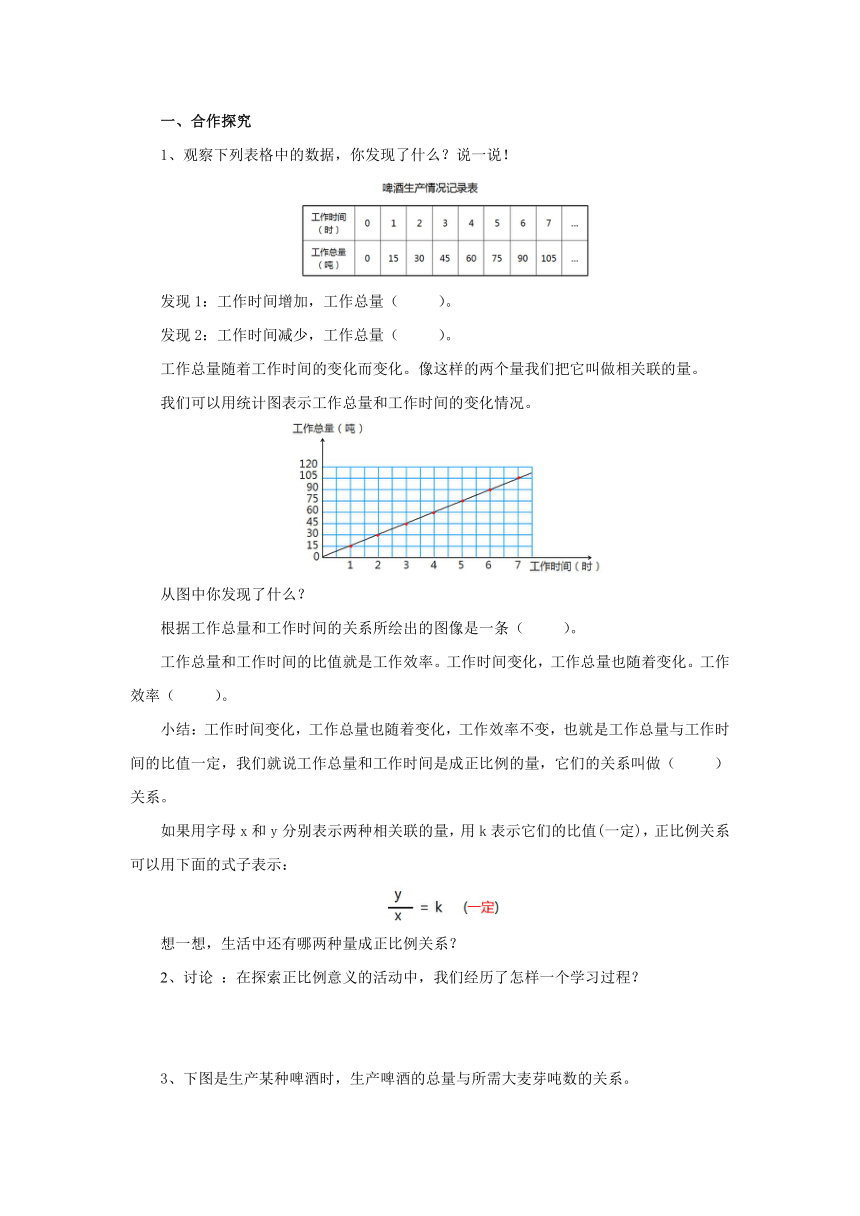
3.3正比例
预习案
一、预习目标及范围
1、使学生正确掌握正比例的意义。掌握判断正比例的方法。
2、会看正比例的图像。
3、让学生感受到正比例在生活中的作用,提高应用的意识和实践能力。
二、预习要点:
1、根据信息窗的信息,随着工作时间的增大,工作总量是怎样变化的?
2、分别计算出工作总量和工作时间的比值吗?,你有什么发现吗?
三、预习检测
1、已知x和y成正比例,请将下表填完整。
2、一辆汽车行驶的路程与时间的关系如下图。
(1)你从图中发现了什么?
(2)根据上图估计一下,要行驶600千米大约需要多少小时 ?
(3)估计一下这辆汽车8.5小时大约行驶多少千米。
探究案
一、合作探究
1、观察下列表格中的数据,你发现了什么?说一说!
发现1:工作时间增加,工作总量( )。
发现2:工作时间减少,工作总量( )。
工作总量随着工作时间的变化而变化。像这样的两个量我们把它叫做相关联的量。
我们可以用统计图表示工作总量和工作时间的变化情况。
从图中你发现了什么?
根据工作总量和工作时间的关系所绘出的图像是一条( )。
工作总量和工作时间的比值就是工作效率。工作时间变化,工作总量也随着变化。工作效率( )。
小结:工作时间变化,工作总量也随着变化,工作效率不变,也就是工作总量与工作时间的比值一定,我们就说工作总量和工作时间是成正比例的量,它们的关系叫做( )关系。
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
想一想,生活中还有哪两种量成正比例关系?
2、讨论 :在探索正比例意义的活动中,我们经历了怎样一个学习过程?
3、下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
(2)根据上图说一说,7吨大麦芽能生产多少吨啤酒?
(3)估计一下,要生产95吨啤酒需要多少吨大麦芽?
二、随堂检测
1、自主练习第1题
“神舟”九号飞船太空飞行情况记录如下:
路程与时间成正比例吗?为什么?
想一想,生活中还有哪两种量成正比例
2、自主练习第2题
3、自主练习第4题
判断下列各题中的两种量是不是成正比例,并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。( )
(2)平行四边形的高一定,它的底与面积。( )
(3)一个人的年龄和体重。( )
(4)正方形的边长与周长。( )
(5)圆的直径一定,圆的周长和圆周率。( )
4、自主练习第10题。将下表填完整。
(1)圆的周长与半径成正比例吗?为什么?
(2)圆的面积与半径成正比例吗?为什么?
(3)你还能找出哪两种量成正比例关系?请说明理由。
5、课件练习
参考答案
一、预习检测
1、
2、
(1)路程与时间成正比例
(2)600 ÷ 80 = 7.5(小时)
(3)80 × 8.5 = 680(千米)
二、随堂检测
1、
2、(1)成正比例
(2)因为比值不一定,所以不成正比例。
3、√ √ × √ ×
4、 周长与半径的比值一定,所以成正比例。
面积和半径的比值不一定,所以不成正比例。
圆的周长与直径成正比例。比值是π ,所以成正比例。
圆的直径与半径成正比例。比值是2 ,所以成正比例。
5、略
预习案
一、预习目标及范围
1、使学生正确掌握正比例的意义。掌握判断正比例的方法。
2、会看正比例的图像。
3、让学生感受到正比例在生活中的作用,提高应用的意识和实践能力。
二、预习要点:
1、根据信息窗的信息,随着工作时间的增大,工作总量是怎样变化的?
2、分别计算出工作总量和工作时间的比值吗?,你有什么发现吗?
三、预习检测
1、已知x和y成正比例,请将下表填完整。
2、一辆汽车行驶的路程与时间的关系如下图。
(1)你从图中发现了什么?
(2)根据上图估计一下,要行驶600千米大约需要多少小时 ?
(3)估计一下这辆汽车8.5小时大约行驶多少千米。
探究案
一、合作探究
1、观察下列表格中的数据,你发现了什么?说一说!
发现1:工作时间增加,工作总量( )。
发现2:工作时间减少,工作总量( )。
工作总量随着工作时间的变化而变化。像这样的两个量我们把它叫做相关联的量。
我们可以用统计图表示工作总量和工作时间的变化情况。
从图中你发现了什么?
根据工作总量和工作时间的关系所绘出的图像是一条( )。
工作总量和工作时间的比值就是工作效率。工作时间变化,工作总量也随着变化。工作效率( )。
小结:工作时间变化,工作总量也随着变化,工作效率不变,也就是工作总量与工作时间的比值一定,我们就说工作总量和工作时间是成正比例的量,它们的关系叫做( )关系。
如果用字母x和y分别表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
想一想,生活中还有哪两种量成正比例关系?
2、讨论 :在探索正比例意义的活动中,我们经历了怎样一个学习过程?
3、下图是生产某种啤酒时,生产啤酒的总量与所需大麦芽吨数的关系。
(1)从图中你可以发现什么?
(2)根据上图说一说,7吨大麦芽能生产多少吨啤酒?
(3)估计一下,要生产95吨啤酒需要多少吨大麦芽?
二、随堂检测
1、自主练习第1题
“神舟”九号飞船太空飞行情况记录如下:
路程与时间成正比例吗?为什么?
想一想,生活中还有哪两种量成正比例
2、自主练习第2题
3、自主练习第4题
判断下列各题中的两种量是不是成正比例,并说明理由。
(1)天数一定,生产零件的总个数与每天生产零件的个数。( )
(2)平行四边形的高一定,它的底与面积。( )
(3)一个人的年龄和体重。( )
(4)正方形的边长与周长。( )
(5)圆的直径一定,圆的周长和圆周率。( )
4、自主练习第10题。将下表填完整。
(1)圆的周长与半径成正比例吗?为什么?
(2)圆的面积与半径成正比例吗?为什么?
(3)你还能找出哪两种量成正比例关系?请说明理由。
5、课件练习
参考答案
一、预习检测
1、
2、
(1)路程与时间成正比例
(2)600 ÷ 80 = 7.5(小时)
(3)80 × 8.5 = 680(千米)
二、随堂检测
1、
2、(1)成正比例
(2)因为比值不一定,所以不成正比例。
3、√ √ × √ ×
4、 周长与半径的比值一定,所以成正比例。
面积和半径的比值不一定,所以不成正比例。
圆的周长与直径成正比例。比值是π ,所以成正比例。
圆的直径与半径成正比例。比值是2 ,所以成正比例。
5、略
