6.9.1策略与方法(一)转化教案1 六年级数学下册-青岛版
文档属性
| 名称 | 6.9.1策略与方法(一)转化教案1 六年级数学下册-青岛版 |

|
|
| 格式 | doc | ||
| 文件大小 | 152.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览

文档简介
6.9.1策略与方法(一)转化
一、复习目标
1、使学生在回顾计算和一些公式推导,体会转化的思想。
2、使学生能通过运用转化的策略分析问题、解决问题、体会转化策略的价值。
3、使学生能根据问题的特点确定具体的转化方法,初步形成策略意识。
二、课时安排:1课时
三、复习重难点:
复习重点:使学生能通过运用转化的策略分析问题、解决问题、体会转化策略的价值。
复习难点:使学生能根据问题的特点确定具体的转化方法,初步形成策略意识。
四、教学过程
(一)知识梳理
我们在解决问题时,遇到一些问题不能直接计算出得数,就需要进行转化。想一想,我们在什么时候运用过转化的方法解决问题?
未知问题转化成已知问题
推导平面图形的面积计算公式
推导立体图形的体积计算公式
解决问题
求不规则物体的体积
(二)题型、方法归纳
1、仔细观察,你有什么发现?
1.2×1.5 12×15÷100
1.25÷0.5 12.5÷5
生讨论交流:
小数乘法可以转化成整数乘法来计算。
小数除法可以转化成除数是整数的除法来计算。
异分母分数加法可以转化成……
师小结:
未知问题转化已知问题
2、生讨论交流:
想一想,学习哪些知识时还用到了转化的方法?
(1)推导平面图形的面积计算公式:
在推导平行四边形面积公式时,用到了转化。把平行四边形转化成长方形。
在推导三角形面积公式时,用到了转化。把三角形转化成平行四边形
在推导梯形面积公式时,用到了转化。把梯形转化成平行四边形
在推导圆面积公式时,用到了转化。把圆转化成长方形。
(2)推导立体图形的体积计算公式:
在推导圆柱体体积公式时,用到了转化。把圆柱转化成长方体
(3)解决问题
合唱队有24人,男生人数是女生人数的,女生有多少人?
分析:可以把分数转化成比,把转化成3:5
24 ÷(3+5)×5=15(人)
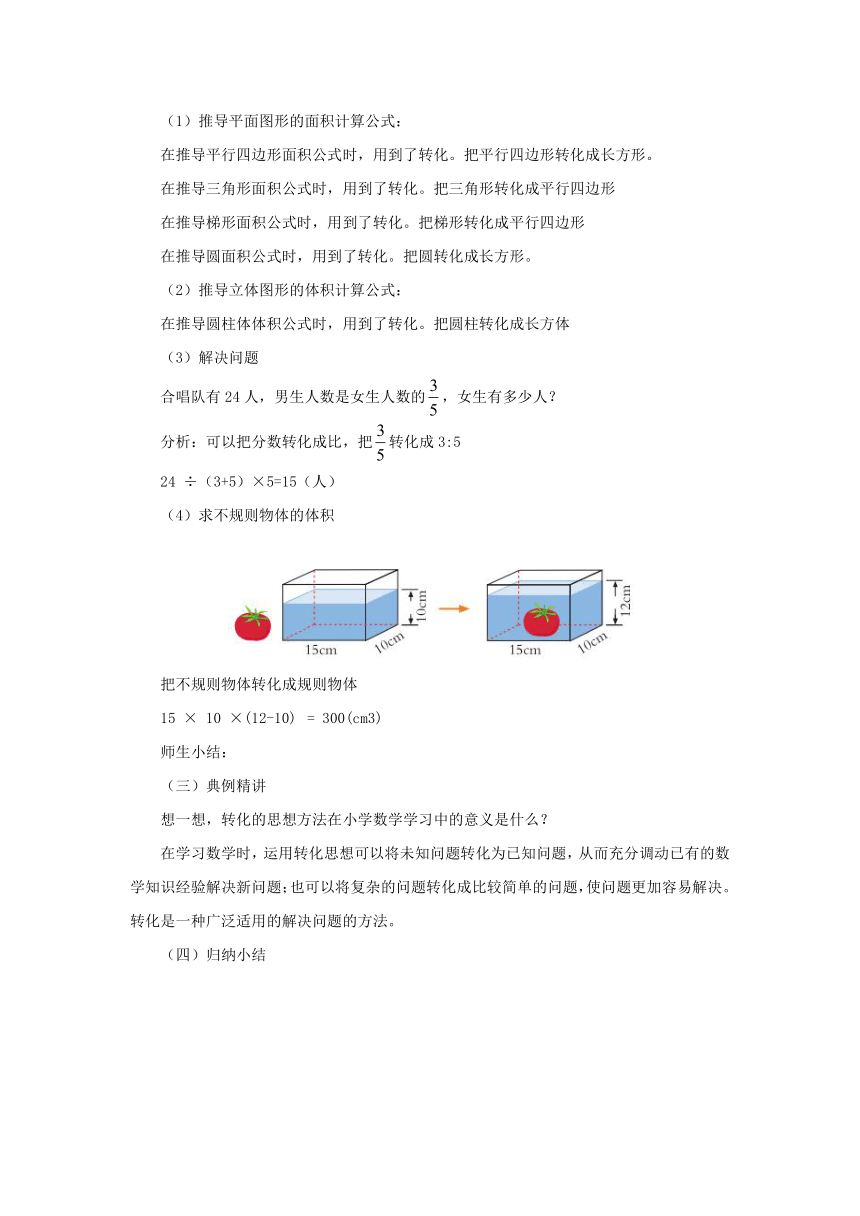
(4)求不规则物体的体积
把不规则物体转化成规则物体
15 × 10 ×(12-10) = 300(cm3)
师生小结:
(三)典例精讲
想一想,转化的思想方法在小学数学学习中的意义是什么?
在学习数学时,运用转化思想可以将未知问题转化为已知问题,从而充分调动已有的数学知识经验解决新问题;也可以将复杂的问题转化成比较简单的问题,使问题更加容易解决。转化是一种广泛适用的解决问题的方法。
(四)归纳小结
(五)随堂检测
1、用分数表示涂色部分。
2、求下面图形的面积。
3、某学校舞蹈队男生人数是女生的,新加入了3名女生后,男生人数是女生的。该学校舞蹈队有男生多少人?
4、一天,爱迪生请他的助手阿普顿帮忙测一只灯泡的容积。阿普顿看着梨形的灯泡,想了好久。画出了一条条复杂的曲线,测量了一个个数据,列了许多道算式,算来算去还没有个结果。爱迪生见他算得满头大汗,于是走上前去帮忙。不到一分钟的时间,爱迪生就解决了问题。
你知道爱迪生是怎样做的吗?
五、板书设计
策略与方法
(转化)
转化
未知问题 → 已知问题
在学习数学时,运用转化思想可以将未知问题转化为已知问题,转化是一种广泛适用的解决问题的方法。
六、作业布置
一个棱长4cm的正方体与一个圆锥体积相等,已知圆锥的高是6cm, 圆锥底面积是多少平方米?
七、教学反思
一、复习目标
1、使学生在回顾计算和一些公式推导,体会转化的思想。
2、使学生能通过运用转化的策略分析问题、解决问题、体会转化策略的价值。
3、使学生能根据问题的特点确定具体的转化方法,初步形成策略意识。
二、课时安排:1课时
三、复习重难点:
复习重点:使学生能通过运用转化的策略分析问题、解决问题、体会转化策略的价值。
复习难点:使学生能根据问题的特点确定具体的转化方法,初步形成策略意识。
四、教学过程
(一)知识梳理
我们在解决问题时,遇到一些问题不能直接计算出得数,就需要进行转化。想一想,我们在什么时候运用过转化的方法解决问题?
未知问题转化成已知问题
推导平面图形的面积计算公式
推导立体图形的体积计算公式
解决问题
求不规则物体的体积
(二)题型、方法归纳
1、仔细观察,你有什么发现?
1.2×1.5 12×15÷100
1.25÷0.5 12.5÷5
生讨论交流:
小数乘法可以转化成整数乘法来计算。
小数除法可以转化成除数是整数的除法来计算。
异分母分数加法可以转化成……
师小结:
未知问题转化已知问题
2、生讨论交流:
想一想,学习哪些知识时还用到了转化的方法?
(1)推导平面图形的面积计算公式:
在推导平行四边形面积公式时,用到了转化。把平行四边形转化成长方形。
在推导三角形面积公式时,用到了转化。把三角形转化成平行四边形
在推导梯形面积公式时,用到了转化。把梯形转化成平行四边形
在推导圆面积公式时,用到了转化。把圆转化成长方形。
(2)推导立体图形的体积计算公式:
在推导圆柱体体积公式时,用到了转化。把圆柱转化成长方体
(3)解决问题
合唱队有24人,男生人数是女生人数的,女生有多少人?
分析:可以把分数转化成比,把转化成3:5
24 ÷(3+5)×5=15(人)
(4)求不规则物体的体积
把不规则物体转化成规则物体
15 × 10 ×(12-10) = 300(cm3)
师生小结:
(三)典例精讲
想一想,转化的思想方法在小学数学学习中的意义是什么?
在学习数学时,运用转化思想可以将未知问题转化为已知问题,从而充分调动已有的数学知识经验解决新问题;也可以将复杂的问题转化成比较简单的问题,使问题更加容易解决。转化是一种广泛适用的解决问题的方法。
(四)归纳小结
(五)随堂检测
1、用分数表示涂色部分。
2、求下面图形的面积。
3、某学校舞蹈队男生人数是女生的,新加入了3名女生后,男生人数是女生的。该学校舞蹈队有男生多少人?
4、一天,爱迪生请他的助手阿普顿帮忙测一只灯泡的容积。阿普顿看着梨形的灯泡,想了好久。画出了一条条复杂的曲线,测量了一个个数据,列了许多道算式,算来算去还没有个结果。爱迪生见他算得满头大汗,于是走上前去帮忙。不到一分钟的时间,爱迪生就解决了问题。
你知道爱迪生是怎样做的吗?
五、板书设计
策略与方法
(转化)
转化
未知问题 → 已知问题
在学习数学时,运用转化思想可以将未知问题转化为已知问题,转化是一种广泛适用的解决问题的方法。
六、作业布置
一个棱长4cm的正方体与一个圆锥体积相等,已知圆锥的高是6cm, 圆锥底面积是多少平方米?
七、教学反思
