6.9.2策略与方法(二)数形结合教案1 六年级数学下册-青岛版
文档属性
| 名称 | 6.9.2策略与方法(二)数形结合教案1 六年级数学下册-青岛版 |  | |
| 格式 | doc | ||
| 文件大小 | 458.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 22:21:47 | ||
图片预览

文档简介
6.9.2策略与方法(二)数形结合
一、复习目标
1、使学生在回顾在学习和探究中所运用的数形结合的方法。
2、使学生能通过运用数形结合的数学思想解决问题、体会数形结合数学思想的优势和作用。
3、使学生能根据问题的特点运用数形结合的重要思想,初步形成策略意识。
二、课时安排:1课时
三、复习重难点:使学生能根据问题的特点运用数形结合的重要思想,初步形成策略意识。
四、教学过程
(一)知识梳理
以前我们学过很多数和形结合的数学例子,回想一下我们是怎样把数与形结合起来解决问题呢?
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
(二)题型、方法归纳
1、统计图是借助图形描述数据的一种直观、有效的形式。
(1)条形统计图是用条形的长短来表示数量的多少。
例如:某电脑公司2011年各种品牌电脑销售情况统计图
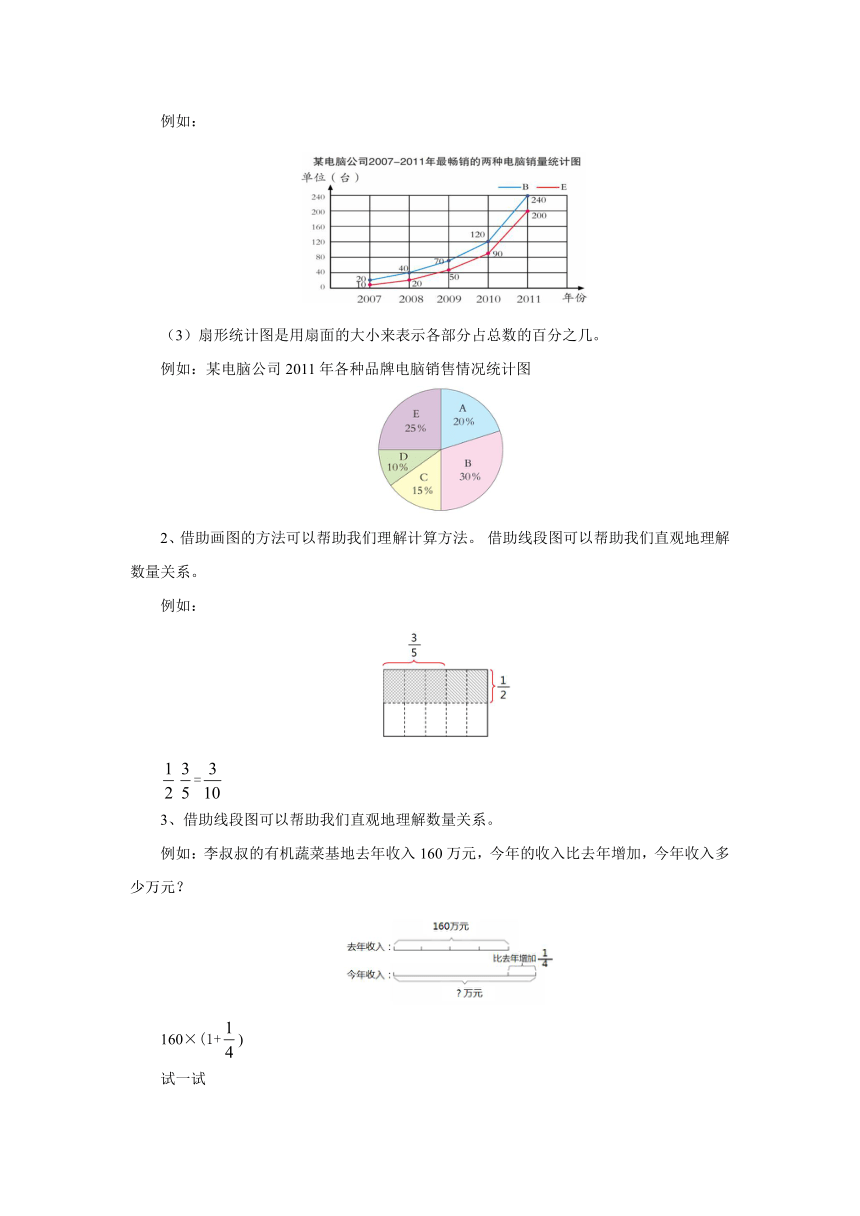
(2)折线统计图是用折线的上升或下降来表示数量的增减变化情况
例如:
(3)扇形统计图是用扇面的大小来表示各部分占总数的百分之几。
例如:某电脑公司2011年各种品牌电脑销售情况统计图
2、借助画图的方法可以帮助我们理解计算方法。 借助线段图可以帮助我们直观地理解数量关系。
例如:
=
3、借助线段图可以帮助我们直观地理解数量关系。
例如:李叔叔的有机蔬菜基地去年收入160万元,今年的收入比去年增加,今年收入多少万元?
160×(1+)
试一试
广场上有一块长方形花坛,长9米。改建时,花坛的长增加了3米,这样花坛的面积就增加了15平方米。花坛原来的面积是多少平方米?(你能用数形结合的方法解答吗 )
先求增加的长方形的宽:
15 ÷ 3 = 5(米)
再求原来长方形的面积:
9 × 5 = 45(平方米)
答:花坛原来的面积是45平方米。
(三)典例精讲
1、正比例图像也是用图形描述成正比例关系的两种量的直观形式。 在平面内确定物体的位置时,也是把数与形结合起来思考。例如:
汽车行驶的时间和路程的变化情况,用图像描述更加形象
2、在平面内确定物体的位置时,也是把数与形结合起来思考。
B在O点北偏东30°方向100米处。
3、师生小结:
结合刚才的梳理过程,说说“数形结合”的主要作用有哪些?
化抽象为直观 化难为易 化繁为简
(四)归纳小结
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
化抽象为直观 化难为易 化繁为简
(五)随堂检测
1、你能用直线上的点表示出下列各数吗?
3, 1.5, -1.5, 0, -0.5
2、看图列式计算。
3、一块菜地种植了4种蔬菜,分布情况如下图。若土豆的种植面积是360㎡,黄瓜的面积比西红柿多多少平方米?
4、灯塔南偏西30°方向15千米处是无名岛,你能在图中表示出它的位置吗?
5、
五、板书设计
策略与方法(数形结合)
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
化抽象为直观 化难为易 化繁为简
六、作业布置
七、教学反思
一、复习目标
1、使学生在回顾在学习和探究中所运用的数形结合的方法。
2、使学生能通过运用数形结合的数学思想解决问题、体会数形结合数学思想的优势和作用。
3、使学生能根据问题的特点运用数形结合的重要思想,初步形成策略意识。
二、课时安排:1课时
三、复习重难点:使学生能根据问题的特点运用数形结合的重要思想,初步形成策略意识。
四、教学过程
(一)知识梳理
以前我们学过很多数和形结合的数学例子,回想一下我们是怎样把数与形结合起来解决问题呢?
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
(二)题型、方法归纳
1、统计图是借助图形描述数据的一种直观、有效的形式。
(1)条形统计图是用条形的长短来表示数量的多少。
例如:某电脑公司2011年各种品牌电脑销售情况统计图
(2)折线统计图是用折线的上升或下降来表示数量的增减变化情况
例如:
(3)扇形统计图是用扇面的大小来表示各部分占总数的百分之几。
例如:某电脑公司2011年各种品牌电脑销售情况统计图
2、借助画图的方法可以帮助我们理解计算方法。 借助线段图可以帮助我们直观地理解数量关系。
例如:
=
3、借助线段图可以帮助我们直观地理解数量关系。
例如:李叔叔的有机蔬菜基地去年收入160万元,今年的收入比去年增加,今年收入多少万元?
160×(1+)
试一试
广场上有一块长方形花坛,长9米。改建时,花坛的长增加了3米,这样花坛的面积就增加了15平方米。花坛原来的面积是多少平方米?(你能用数形结合的方法解答吗 )
先求增加的长方形的宽:
15 ÷ 3 = 5(米)
再求原来长方形的面积:
9 × 5 = 45(平方米)
答:花坛原来的面积是45平方米。
(三)典例精讲
1、正比例图像也是用图形描述成正比例关系的两种量的直观形式。 在平面内确定物体的位置时,也是把数与形结合起来思考。例如:
汽车行驶的时间和路程的变化情况,用图像描述更加形象
2、在平面内确定物体的位置时,也是把数与形结合起来思考。
B在O点北偏东30°方向100米处。
3、师生小结:
结合刚才的梳理过程,说说“数形结合”的主要作用有哪些?
化抽象为直观 化难为易 化繁为简
(四)归纳小结
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
化抽象为直观 化难为易 化繁为简
(五)随堂检测
1、你能用直线上的点表示出下列各数吗?
3, 1.5, -1.5, 0, -0.5
2、看图列式计算。
3、一块菜地种植了4种蔬菜,分布情况如下图。若土豆的种植面积是360㎡,黄瓜的面积比西红柿多多少平方米?
4、灯塔南偏西30°方向15千米处是无名岛,你能在图中表示出它的位置吗?
5、
五、板书设计
策略与方法(数形结合)
统计图是借助图形描述数据的一种直观、有效的形式。
借助画图的方法可以帮助我们理解计算方法。
借助线段图可以帮助我们直观地理解数量关系。
正比例图像也是用图形描述成正比例关系的两种量的直观形式。
在平面内确定物体的位置时,也是把数与形结合起来思考。
化抽象为直观 化难为易 化繁为简
六、作业布置
七、教学反思
