4.3比例的应用同步练习六年级数学下册(人教版)(含解析)
文档属性
| 名称 | 4.3比例的应用同步练习六年级数学下册(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 22:44:37 | ||
图片预览




文档简介
4.3比例的应用 同步练习 六年级数学下册(人教版)含答案
一、填空题
1.一个圆柱形零件的高是7mm,在图纸上的高是21cm。这幅图纸的比例尺是( )。
2.在一幅比例尺为1∶5000000的地图上,量得杭州到上海的距离是3.4cm,杭州到上海的实际距离是( )km。
3.在一幅地图上标出的线段比例尺为:,把它改写成数值比例尺的形式是( );如果两地之间的距离为360km,那么在这幅地图上的图上距离是( )cm。
4.一个精密零件长5mm,画在图纸上是4cm,这张图纸的比例尺是( )。
5.下图是甲乙两城在地图上的位置,从图上可知,乙城在甲城的( )方向,实际距离是( )千米。
6.在一幅地图上,2厘米表示实际距离120千米,这幅地图的比例尺是( ),甲、乙两地相距660千米,在这幅地图上的距离是( )厘米。
二、选择题
7.在一幅地图上量得一块长方形公园长2cm,宽1cm,已知这幅地图的比例尺是1∶5000,这个公园的实际面积是( )m2。
A.5000 B.500 C.300
8.在一幅地图上的比例尺为1∶50000,现在如果改为1∶20000的比例尺,则原来图上10厘米的距离,现在应画( )厘米。
A.2.5 B.5 C.25
9.下面说法正确的是( )。
A.故事书的总页数一定,已看的页数和未看的页数成正比例关系
B.出米率一定,大米的质量与稻谷的质量成正比例关系
C.一幅地图上的比例尺是1∶10,表示把实际距离在图上放大10倍
10.一个圆形广场的周长是314米,把它画在1∶1000的图纸上,图纸上的面积是( )。
A.7.85平方米 B.7.85平方厘米 C.78.5平方厘米
11.一个零件长0.6cm,画在一幅图上长18cm。这幅图的比例尺是( )。
A. B. C.
三、判断题
12.无论是把图形放大还是缩小,它的形状是不变的。( )
13.一个图形按照一定的比例放大或缩小后,形状和大小都发生了改变。( )
14.在比例尺是1∶5000000的地图上,图上1cm表示实际50km。( )
15.当实际距离一定时,比例尺越大图上距离就画得越长。( )
16.图形的放大与缩小就是把原图形各边加上或减去一个相同的数。( )
17.一张图纸的比例尺是5∶1,该图表示的图上距离大于实际距离。( )
18.把一个长方形按3∶1放大,它的面积就扩大到原来的6倍。( )
19.把线段比例尺改写成数值比例尺是1∶8000000。(每一小段有1厘米)( )
四、解答题
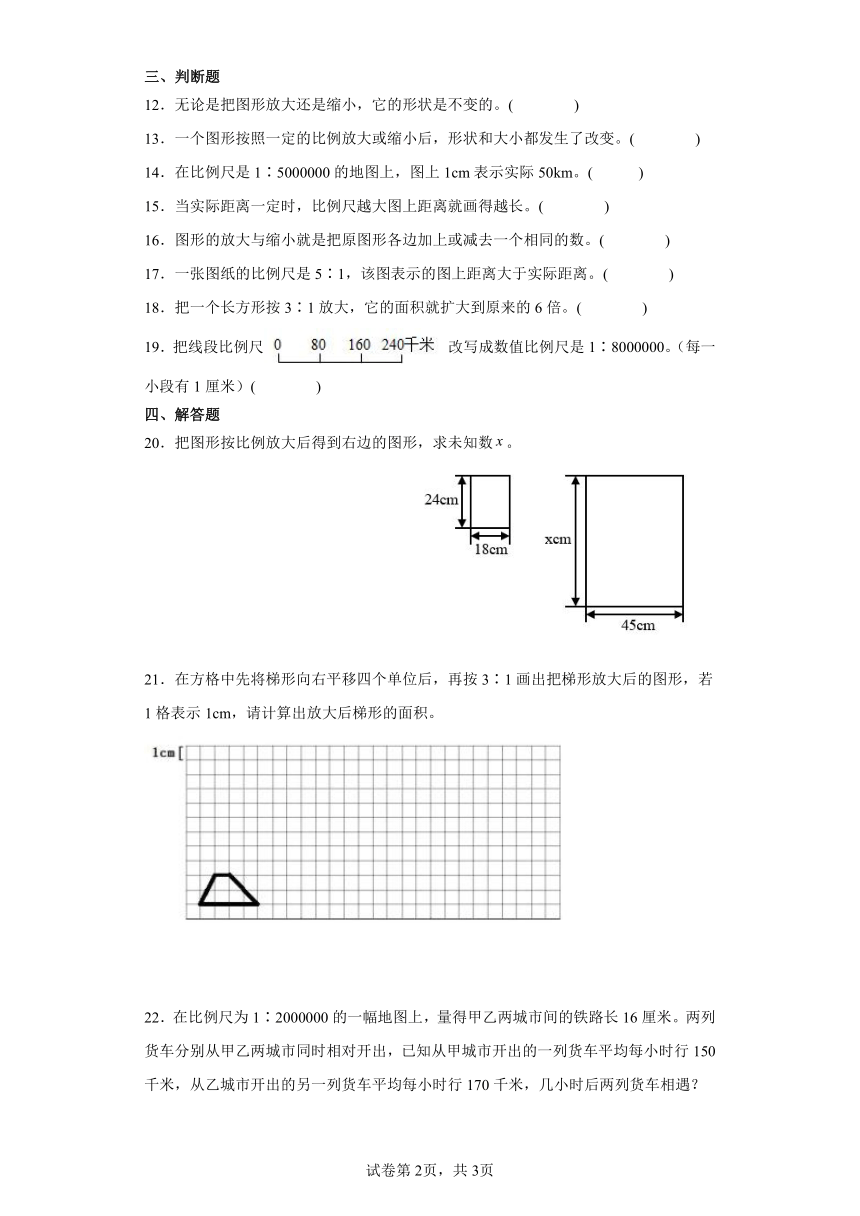
20.把图形按比例放大后得到右边的图形,求未知数。
21.在方格中先将梯形向右平移四个单位后,再按3∶1画出把梯形放大后的图形,若1格表示1cm,请计算出放大后梯形的面积。
22.在比例尺为1∶2000000的一幅地图上,量得甲乙两城市间的铁路长16厘米。两列货车分别从甲乙两城市同时相对开出,已知从甲城市开出的一列货车平均每小时行150千米,从乙城市开出的另一列货车平均每小时行170千米,几小时后两列货车相遇?
23.在比例尺是1∶40000000的地图上,量得兰州到乌鲁木齐的铁路线的距离为4.8cm,兰州到乌鲁木齐两地间的实际距离约是多少千米?
24.自来水厂要建一个圆柱形过滤塔,在比例尺是1∶100的图纸上,标注塔底周长是18.84厘米,高是4厘米。这个过滤塔建成后最多可容纳多少立方米的水?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.30:1
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求出这幅图的比例尺。
【详解】7mm=0.7cm
21cm:0.7cm=30:1
所以这幅图的比例尺是30:1
2.170
【分析】根据实际距离=图上距离÷比例尺,据此进行计算即可。
【详解】3.4÷
=3.4×5000000
=17000000(cm)
=170(km)
则杭州到上海的实际距离是170km。
3. 1∶3000000 12
【分析】观察线段比例尺可知,图上1cm表示实际距离为30km,根据图上距离∶实际距离=比例尺,据此计算即可;再根据图上距离=实际距离×比例尺,据此解答即可。
【详解】1cm∶30km
=1cm∶3000000cm
=1∶3000000
360km=36000000cm
36000000×=12(cm)
则把它改写成数值比例尺的形式是1∶3000000;如果两地之间的距离为360km,那么在这幅地图上的图上距离是12cm。
4.8∶1
【分析】图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,将后项化成1即可。
【详解】4cm∶5mm=40mm∶5mm=8∶1
一个精密零件长5mm,画在图纸上是4cm,这张图纸的比例尺是8∶1。
5.东偏北30° 180
【分析】根据图上确定方向的方法:上北下南、左西右东,以甲城为观测点,即可确定乙城的方向,量得甲城到乙城的图上距离是3厘米,然后根据图上1厘米表示实际60千米,求出甲城到乙城的实际距离。
【详解】3×60=180(千米)
乙城在甲城的东偏北30°方向;实际距离是180千米。
6. 1∶6000000 11
【分析】图上距离和实际距离已知,依据“比例尺=图上距离∶实际距离”即可求得这幅图的比例尺;再据“图上距离=实际距离×比例尺”即可求得两地的图上距离。
【详解】因为120千米=12000000厘米
则2厘米∶12000000厘米∶6000000
又因660千米=66000000厘米,
所以(厘米)
这幅地图的比例尺是1∶6000000;甲、乙两地相距660千米,在这幅地图上的距离是11厘米。
7.A
【分析】根据“实际距离=图上距离÷比例尺”,求出长方形公园的实际长和实际宽,再根据长方形的面积=长×宽,求出这个公园的实际面积。注意单位的换算:1m=100cm。
【详解】实际长:
2÷
=2×5000
=10000(cm)
10000cm=100m
实际宽:
1÷
=1×5000
=5000(cm)
5000cm=50m
实际面积:
100×50=5000(m2)
这个公园的实际面积是5000m2。
故答案为:A
8.C
【分析】先依据“实际距离=图上距离÷比例尺”求出10厘米的实际距离,进而依据图上距离=实际距离×比例尺”即可求出在新地图中的图上距离。
【详解】10÷
=10×50000
=500000(厘米)
500000×
=25(厘米)
即现在应画25厘米。
故答案为:C
9.B
【分析】题干选项中成正比例关系是:两个量的比值一定,则这两个量成正比例关系;比例尺=图上距离∶实际距离,根据相关知识点解答。
【详解】A.故事书的页数一定,已看页数+未看页数=书本总页数,不成正比例关系;
B.出米率=大米质量÷稻谷质量×100%,出米率一定,即两者比值一定,故大米的质量与稻谷的质量成正比例关系;
C.比例尺=图上距离∶实际距离,表示的是把实际距离缩小10倍;
故答案为:B
10.C
【分析】根据圆的半径=周长÷π÷2,求出半径,再根据实际距离×比例尺=图上距离,求出图上圆的半径,最后根据圆的面积=πr2,求出图上面积即可。
【详解】314÷3.14÷2=50(米)
50×=0.05(米)=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
图纸上的面积是78.5平方厘米。
故答案为:C
11.A
【分析】比例尺=图上距离∶实际距离,把题中数据代入公式计算,据此解答。
【详解】18cm∶0.6cm=180∶6=(180÷6)∶(6÷6)=30∶1
故答案为:A
12.√
【详解】根据图形放大与缩小的意义,一个图形放大或缩小,其对应边就放大或缩小,但放大或缩小后的形状不变,即放大或缩小后的图形大小发生变化,形状不变。
例如长方形按1∶2缩小,缩小后形状不变。
故答案为:√
13.×
【分析】保持图形原来的形状而使图形变小,叫做图形的缩小;保持图形原来的形状而使图形变大,叫做图形的放大。据此进行判断即可。
【详解】把一个图形放大或缩小后得到的图形与原来的图形相比,形状相同,大小不同。所以原题说法错误。
故答案为:×
14.√
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【详解】比例尺是1∶5000000的地图上,图上1cm表示实际距离5000000cm,
5000000cm=50km
即图上1cm表示实际距离50km,本题说法正确。
故答案为:√
15.√
【分析】根据比例尺的定义:,可推导出:
由此可知图上距离与比例尺成正比例,比例尺越大,则图上距离也越大。据此判断。
【详解】因为:
所以:
图上距离与比例尺成正比例,比例尺越大,则图上距离也越大,画得也越长。
故原题答案:√
16.×
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1;把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【详解】图形放大或缩小的倍数是指对应边放大或缩小的倍数。
故答案为:×
17.√
【分析】比例尺=图上距离∶实际距离,据此分析这张图纸的比例尺5∶1的意义即可。
【详解】比例尺是5∶1表示图上距离5厘米,代表实际距离1厘米,图上距离是实际距离的5倍,则该图表示的图上距离大于实际距离。
故答案为: √
18.×
【分析】把一个长方形按3∶1放大,面积按照32∶12放大,据此确定面积扩大到原来的倍数。
【详解】32∶12=9∶1,把一个长方形按3∶1放大,它的面积就扩大到原来的9倍,所以原题说法错误。
故答案为:×
19.√
【分析】根据比例尺的意义可知,题目中的线段比例尺表示图上1厘米代表实际距离80千米,根据比例尺=图上距离∶实际距离,单位换算后代入数据即可求出数值比例尺。
【详解】1厘米∶80千米
=1厘米∶8000000厘米
=1∶8000000
改写成数值比例尺是1∶8000000。
故答案为:√
20.
【分析】根据可知:,据此关系式列出比例,再根据比例的基本性质解比例求出未知数x的值。
【详解】
解:
21.图见详解;45cm2
【分析】根据平移的特征,把梯形的四个顶点分别向右平移4格,依次连结各点即可画出将梯形向右平移四个单位后的图形;按3∶1的比例画出梯形放大后的图形,就是把原梯形的上底、下底和高分别扩大到原来的3倍,原梯形的上底、下底和高分别是1格、4格和2格,扩大后的梯形的上底、下底和高分别是3格、12格和6格,最后根据梯形的面积=(上底+下底)×高÷2代入数据进行解答即可。
【详解】作图如下:
放大后梯形的面积:
(3+12)×6÷2
=15×6÷2
=90÷2
=45(cm2)
22.1小时
【分析】根据实际距离=图上距离÷比例尺,据此求出甲乙两城市之间的距离,再根据相遇问题中,路程÷速度和=相遇时间,据此解答即可。
【详解】16÷=32000000(厘米)=320(千米)
320÷(150+170)
=320÷320
=1(小时)
答:1小时后两列货车相遇。
23.1920
【分析】已知兰州到乌鲁木齐的铁路距离、比例尺,根据“实际距离=图上距离÷比例尺”即可解答。
【详解】4.8÷=192000000(厘米)
192000000厘米=1920千米
答:兰州到乌鲁木齐的实际距离是1920千米。
24.113.04立方米
【分析】根据实际距离=图上距离÷比例尺,代入数据求出水塔的底面直径和高;再将数据代入圆柱的容积公式求出容积即可。
【详解】18.84×100÷100
=1884÷100
=18.84(米)
4×100÷100
=400÷100
=4(米)
3.14×(18.84÷3.14÷2)2×4
=3.14×(6÷2)2×4
=3.14×32×4
=3.14×9×4
=28.26×4
=113.04(立方米)
答:这个过滤塔建成后最多可容纳113.04立方米的水。
答案第1页,共2页
答案第1页,共2页
一、填空题
1.一个圆柱形零件的高是7mm,在图纸上的高是21cm。这幅图纸的比例尺是( )。
2.在一幅比例尺为1∶5000000的地图上,量得杭州到上海的距离是3.4cm,杭州到上海的实际距离是( )km。
3.在一幅地图上标出的线段比例尺为:,把它改写成数值比例尺的形式是( );如果两地之间的距离为360km,那么在这幅地图上的图上距离是( )cm。
4.一个精密零件长5mm,画在图纸上是4cm,这张图纸的比例尺是( )。
5.下图是甲乙两城在地图上的位置,从图上可知,乙城在甲城的( )方向,实际距离是( )千米。
6.在一幅地图上,2厘米表示实际距离120千米,这幅地图的比例尺是( ),甲、乙两地相距660千米,在这幅地图上的距离是( )厘米。
二、选择题
7.在一幅地图上量得一块长方形公园长2cm,宽1cm,已知这幅地图的比例尺是1∶5000,这个公园的实际面积是( )m2。
A.5000 B.500 C.300
8.在一幅地图上的比例尺为1∶50000,现在如果改为1∶20000的比例尺,则原来图上10厘米的距离,现在应画( )厘米。
A.2.5 B.5 C.25
9.下面说法正确的是( )。
A.故事书的总页数一定,已看的页数和未看的页数成正比例关系
B.出米率一定,大米的质量与稻谷的质量成正比例关系
C.一幅地图上的比例尺是1∶10,表示把实际距离在图上放大10倍
10.一个圆形广场的周长是314米,把它画在1∶1000的图纸上,图纸上的面积是( )。
A.7.85平方米 B.7.85平方厘米 C.78.5平方厘米
11.一个零件长0.6cm,画在一幅图上长18cm。这幅图的比例尺是( )。
A. B. C.
三、判断题
12.无论是把图形放大还是缩小,它的形状是不变的。( )
13.一个图形按照一定的比例放大或缩小后,形状和大小都发生了改变。( )
14.在比例尺是1∶5000000的地图上,图上1cm表示实际50km。( )
15.当实际距离一定时,比例尺越大图上距离就画得越长。( )
16.图形的放大与缩小就是把原图形各边加上或减去一个相同的数。( )
17.一张图纸的比例尺是5∶1,该图表示的图上距离大于实际距离。( )
18.把一个长方形按3∶1放大,它的面积就扩大到原来的6倍。( )
19.把线段比例尺改写成数值比例尺是1∶8000000。(每一小段有1厘米)( )
四、解答题
20.把图形按比例放大后得到右边的图形,求未知数。
21.在方格中先将梯形向右平移四个单位后,再按3∶1画出把梯形放大后的图形,若1格表示1cm,请计算出放大后梯形的面积。
22.在比例尺为1∶2000000的一幅地图上,量得甲乙两城市间的铁路长16厘米。两列货车分别从甲乙两城市同时相对开出,已知从甲城市开出的一列货车平均每小时行150千米,从乙城市开出的另一列货车平均每小时行170千米,几小时后两列货车相遇?
23.在比例尺是1∶40000000的地图上,量得兰州到乌鲁木齐的铁路线的距离为4.8cm,兰州到乌鲁木齐两地间的实际距离约是多少千米?
24.自来水厂要建一个圆柱形过滤塔,在比例尺是1∶100的图纸上,标注塔底周长是18.84厘米,高是4厘米。这个过滤塔建成后最多可容纳多少立方米的水?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.30:1
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求出这幅图的比例尺。
【详解】7mm=0.7cm
21cm:0.7cm=30:1
所以这幅图的比例尺是30:1
2.170
【分析】根据实际距离=图上距离÷比例尺,据此进行计算即可。
【详解】3.4÷
=3.4×5000000
=17000000(cm)
=170(km)
则杭州到上海的实际距离是170km。
3. 1∶3000000 12
【分析】观察线段比例尺可知,图上1cm表示实际距离为30km,根据图上距离∶实际距离=比例尺,据此计算即可;再根据图上距离=实际距离×比例尺,据此解答即可。
【详解】1cm∶30km
=1cm∶3000000cm
=1∶3000000
360km=36000000cm
36000000×=12(cm)
则把它改写成数值比例尺的形式是1∶3000000;如果两地之间的距离为360km,那么在这幅地图上的图上距离是12cm。
4.8∶1
【分析】图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,将后项化成1即可。
【详解】4cm∶5mm=40mm∶5mm=8∶1
一个精密零件长5mm,画在图纸上是4cm,这张图纸的比例尺是8∶1。
5.东偏北30° 180
【分析】根据图上确定方向的方法:上北下南、左西右东,以甲城为观测点,即可确定乙城的方向,量得甲城到乙城的图上距离是3厘米,然后根据图上1厘米表示实际60千米,求出甲城到乙城的实际距离。
【详解】3×60=180(千米)
乙城在甲城的东偏北30°方向;实际距离是180千米。
6. 1∶6000000 11
【分析】图上距离和实际距离已知,依据“比例尺=图上距离∶实际距离”即可求得这幅图的比例尺;再据“图上距离=实际距离×比例尺”即可求得两地的图上距离。
【详解】因为120千米=12000000厘米
则2厘米∶12000000厘米∶6000000
又因660千米=66000000厘米,
所以(厘米)
这幅地图的比例尺是1∶6000000;甲、乙两地相距660千米,在这幅地图上的距离是11厘米。
7.A
【分析】根据“实际距离=图上距离÷比例尺”,求出长方形公园的实际长和实际宽,再根据长方形的面积=长×宽,求出这个公园的实际面积。注意单位的换算:1m=100cm。
【详解】实际长:
2÷
=2×5000
=10000(cm)
10000cm=100m
实际宽:
1÷
=1×5000
=5000(cm)
5000cm=50m
实际面积:
100×50=5000(m2)
这个公园的实际面积是5000m2。
故答案为:A
8.C
【分析】先依据“实际距离=图上距离÷比例尺”求出10厘米的实际距离,进而依据图上距离=实际距离×比例尺”即可求出在新地图中的图上距离。
【详解】10÷
=10×50000
=500000(厘米)
500000×
=25(厘米)
即现在应画25厘米。
故答案为:C
9.B
【分析】题干选项中成正比例关系是:两个量的比值一定,则这两个量成正比例关系;比例尺=图上距离∶实际距离,根据相关知识点解答。
【详解】A.故事书的页数一定,已看页数+未看页数=书本总页数,不成正比例关系;
B.出米率=大米质量÷稻谷质量×100%,出米率一定,即两者比值一定,故大米的质量与稻谷的质量成正比例关系;
C.比例尺=图上距离∶实际距离,表示的是把实际距离缩小10倍;
故答案为:B
10.C
【分析】根据圆的半径=周长÷π÷2,求出半径,再根据实际距离×比例尺=图上距离,求出图上圆的半径,最后根据圆的面积=πr2,求出图上面积即可。
【详解】314÷3.14÷2=50(米)
50×=0.05(米)=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
图纸上的面积是78.5平方厘米。
故答案为:C
11.A
【分析】比例尺=图上距离∶实际距离,把题中数据代入公式计算,据此解答。
【详解】18cm∶0.6cm=180∶6=(180÷6)∶(6÷6)=30∶1
故答案为:A
12.√
【详解】根据图形放大与缩小的意义,一个图形放大或缩小,其对应边就放大或缩小,但放大或缩小后的形状不变,即放大或缩小后的图形大小发生变化,形状不变。
例如长方形按1∶2缩小,缩小后形状不变。
故答案为:√
13.×
【分析】保持图形原来的形状而使图形变小,叫做图形的缩小;保持图形原来的形状而使图形变大,叫做图形的放大。据此进行判断即可。
【详解】把一个图形放大或缩小后得到的图形与原来的图形相比,形状相同,大小不同。所以原题说法错误。
故答案为:×
14.√
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【详解】比例尺是1∶5000000的地图上,图上1cm表示实际距离5000000cm,
5000000cm=50km
即图上1cm表示实际距离50km,本题说法正确。
故答案为:√
15.√
【分析】根据比例尺的定义:,可推导出:
由此可知图上距离与比例尺成正比例,比例尺越大,则图上距离也越大。据此判断。
【详解】因为:
所以:
图上距离与比例尺成正比例,比例尺越大,则图上距离也越大,画得也越长。
故原题答案:√
16.×
【分析】把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1;把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【详解】图形放大或缩小的倍数是指对应边放大或缩小的倍数。
故答案为:×
17.√
【分析】比例尺=图上距离∶实际距离,据此分析这张图纸的比例尺5∶1的意义即可。
【详解】比例尺是5∶1表示图上距离5厘米,代表实际距离1厘米,图上距离是实际距离的5倍,则该图表示的图上距离大于实际距离。
故答案为: √
18.×
【分析】把一个长方形按3∶1放大,面积按照32∶12放大,据此确定面积扩大到原来的倍数。
【详解】32∶12=9∶1,把一个长方形按3∶1放大,它的面积就扩大到原来的9倍,所以原题说法错误。
故答案为:×
19.√
【分析】根据比例尺的意义可知,题目中的线段比例尺表示图上1厘米代表实际距离80千米,根据比例尺=图上距离∶实际距离,单位换算后代入数据即可求出数值比例尺。
【详解】1厘米∶80千米
=1厘米∶8000000厘米
=1∶8000000
改写成数值比例尺是1∶8000000。
故答案为:√
20.
【分析】根据可知:,据此关系式列出比例,再根据比例的基本性质解比例求出未知数x的值。
【详解】
解:
21.图见详解;45cm2
【分析】根据平移的特征,把梯形的四个顶点分别向右平移4格,依次连结各点即可画出将梯形向右平移四个单位后的图形;按3∶1的比例画出梯形放大后的图形,就是把原梯形的上底、下底和高分别扩大到原来的3倍,原梯形的上底、下底和高分别是1格、4格和2格,扩大后的梯形的上底、下底和高分别是3格、12格和6格,最后根据梯形的面积=(上底+下底)×高÷2代入数据进行解答即可。
【详解】作图如下:
放大后梯形的面积:
(3+12)×6÷2
=15×6÷2
=90÷2
=45(cm2)
22.1小时
【分析】根据实际距离=图上距离÷比例尺,据此求出甲乙两城市之间的距离,再根据相遇问题中,路程÷速度和=相遇时间,据此解答即可。
【详解】16÷=32000000(厘米)=320(千米)
320÷(150+170)
=320÷320
=1(小时)
答:1小时后两列货车相遇。
23.1920
【分析】已知兰州到乌鲁木齐的铁路距离、比例尺,根据“实际距离=图上距离÷比例尺”即可解答。
【详解】4.8÷=192000000(厘米)
192000000厘米=1920千米
答:兰州到乌鲁木齐的实际距离是1920千米。
24.113.04立方米
【分析】根据实际距离=图上距离÷比例尺,代入数据求出水塔的底面直径和高;再将数据代入圆柱的容积公式求出容积即可。
【详解】18.84×100÷100
=1884÷100
=18.84(米)
4×100÷100
=400÷100
=4(米)
3.14×(18.84÷3.14÷2)2×4
=3.14×(6÷2)2×4
=3.14×32×4
=3.14×9×4
=28.26×4
=113.04(立方米)
答:这个过滤塔建成后最多可容纳113.04立方米的水。
答案第1页,共2页
答案第1页,共2页
