湖南省湖南师大附高2022-2023学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 湖南省湖南师大附高2022-2023学年高二下学期期中考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 948.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-01 11:50:53 | ||
图片预览




文档简介
湖南师大附高2022-2023学年高二下学期期中考试
数学
时量:120分钟 满分:150分
得分:___________
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合,则( )
A. B. C. D.
2.设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
3.若函数的值域为,则函数的大致图象是( )
A. B. C. D.
4.一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员先将的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.你认为顾客购得的黄金
附:依据力矩平衡原理,天平平衡时有,其中分别为左右盘中物体质量,分别为左右横梁臂长.( )
A.等于 B.小于 C.大于 D.不确定
5.天文学中常用“星等”来衡量天空中星体的明亮程度,一个望远镜能看到的最暗的天体星等称为这个望远镜的“极限星等”.在一定条件下,望远镜的极限星等M与其口径D(即物镜的直径,单位:)近似满足关系式,例如:口径的望远镜的极限星等约为10.3.则口径的望远镜的极限星等约为( )
A.12.8 B.13.3 C.13.8 D.14.3
6.2023年3月,某校A,B,C,D,E,F六名同学参加了中学生地球科学奥林匹克竞赛,均在比赛中取得优异成绩,现这6名同学和他们的主教练共7人站成一排合影留念,则主教练和A站在两端,B、C相邻,B、D不相邻的排法种数为( )
A.36 B.48 C.56 D.72
7.已知,则( )
A. B. C. D.
8.记设函数,若函数恰有三个零点,则实数m的取值范围的是( )
A. B.
C. D.
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对的得2分,有选错的得0分.)
9.若,则下列不等式正确的是( )
A. B. C. D.
10.某计算机程序每运行一次都随机出现一个n位二进制数,其中,若在A的各数位上出现0和1的概率均为且相互独立,记,则当程序运行一次时( )
A.
B.
C.X的数学期望
D.X的方差
11.红黄蓝被称为三原色,选取任意几种颜色调配,可以调配出其他颜色.已知同一种颜色混合颜色不变,等量的红色加黄色调配出橙色;等量的红色加蓝色调配出紫色;等量的黄色加蓝色调配出绿色.现有红黄蓝彩色颜料各两瓶,甲从六瓶中任取两瓶颜料,乙再从余下四瓶中任取两瓶颜料,两人分别进行等量调配,A表示事件“甲调配出红色”;B表示事件“甲调配出绿色”;C表示事件“乙调配出紫色”,则下列说法正确的是( )
A.事件A与事件C是独立事件 B.事件A与事件B是互斥事件
C. D.
12.对于定义在区间D上的函数,若满足:且,都有,则称函数为区间D上的“非减函数”.若为区间上的“非减函数”,且,,又当时,恒成立,下列命题中正确的有( )
A. B.
C. D.
三、填空题(本大题共4小题,每小题5分,共20分.)
13.已知,则的最小值为_____________.
14.已知函数的值域为,则k的取值范围是____________.
15.已知,则___________.(用数字作答)
16.若对于任意实数x及,均有,则实数a的取值范围是_____________.
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.)
17.(本小题满分10分)
已知关于x的函数,其中.
(1)当时,求的值域;
(2)若当时,函数的图象总在直线的上方,为整数,求的值.
18.(本小题满分12分)
已知函数.
(1)若不等式对于一切实数x恒成立,求实数a的取值范围;
(2)若,解关于x的不等式.
19.(本小题满分12分)
如图,在直三棱柱中,E,F分别是棱的中点,.
(1)证明:;
(2)若,平面与平面所成锐二面角的余弦值为,求直线与平面所成角的正弦值.
20.(本小题满分12分)
云计算是信息技术发展的集中体现,近年来,我国云计算市场规模持续增长.从中国信息通信研究院发布的《云计算白皮书(2022年)》可知,我国2017年至2021年云计算市场规模数据统计表如下:
年份 2017年 2018年 2019年 2020年 2021年
年份代码x 1 2 3 4 5
云计算市场规模y/亿元 692 962 1334 2091 3229
经计算得:.
(1)根据以上数据,建立y关于x的回归方程(e为自然对数的底数);
(2)云计算为企业降低生产成本、提升产品质量提供了强大助推力.某企业未引入云计算前,单件产品尺寸与标准品尺寸的误差,其中m为单件产品的成本(单位:元),且;引入云计算后,单件产品尺寸与标准品尺寸的误差,若保持单件产品的成本不变,则将会变成多少?若保持产品质量不变(即误差的概率分布不变),则单件产品的成本将会下降多少?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为.
若,则.
21.(本小题满分12分)
2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市.为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会
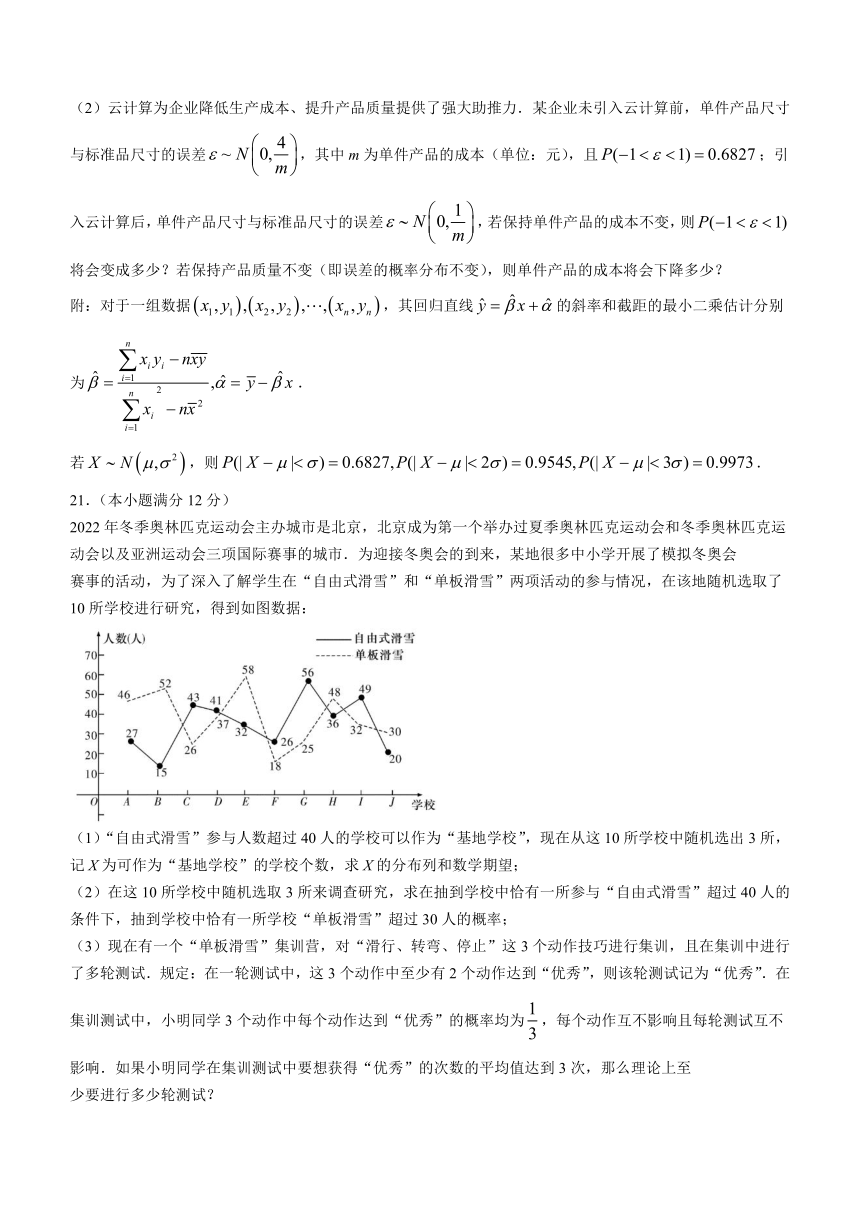
赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如图数据:
(1)“自由式滑雪”参与人数超过40人的学校可以作为“基地学校”,现在从这10所学校中随机选出3所,记X为可作为“基地学校”的学校个数,求X的分布列和数学期望;
(2)在这10所学校中随机选取3所来调查研究,求在抽到学校中恰有一所参与“自由式滑雪”超过40人的条件下,抽到学校中恰有一所学校“单板滑雪”超过30人的概率;
(3)现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到“优秀”,则该轮测试记为“优秀”.在集训测试中,小明同学3个动作中每个动作达到“优秀”的概率均为,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到3次,那么理论上至
少要进行多少轮测试?
22.(本小题满分12分)
已知函数,函数.函数.
(1)求不等式的解集;
(2)若存在,使得成立,求实数a的取值范围;
(3)定义在I上的函数,如果满足:对任意,存在常数,都有成立,则称函数是I上的有界函数,其中M称为函数在I的上界.讨论函数在上是否存在上界?若存在,求出M的取值范围;若不存在,请说明理由.
数学参考答案
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
题号 1 2 3 4 5 6 7 8
答案 C B A C B D A B
1.C 【解析】由得:,而,
所以.
故选:C.
2.B 【解析】由可得,即,可等价变形为:,即或,显然“或”是“”的必要不充分条件.
故选:B.
3.A 【解析】∵,且的值域为,∴,
当时,在上是增函数.
又函数的图象关于y轴对称,
所以的大致图象应为选项A.
故选:A.
4.C 【解析】设天平左臂长,右臂长,且,
设天平右盘有克黄金,天平左盘有克黄金,
所以
所以.
故选:C.
5.B 【解析】由题意,∴,∴.
∴.
故选:B.
6.D 【解析】分2步进行分析:
①主教练和A站在两端,有种情况;
②中间5人分2种情况讨论:
若B、C相邻且与D相邻,有种安排方法;
若B、C相邻且不与D相邻,有种安排方法,
则中间5人有种安排方法,则共有种不同的安排方法.故选:D.
7.A 【解析】;
设,因为函数在上递增,,,即,由零点存在定理可知;
设函数,易知在上递减,,即,由零点存在定理可知.即.故选:A.
8.B 【解析】设,
则函数在上递增,且,且函数至多有两个零点,
当时,,
若函数在上有零点,则在上有零点,不妨设零,点为,则,
此时,则,与题意矛盾,
故函数在上无零点.
二次函数图象对称销为直线,函数在上有两个零点,所以
解得故选:B.
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对的得2分,有选错的得0分.)
题号 9 10 11 12
答案 AC ABC BD ACD
9.AC 【解析】由,可知.
A中,因为.所以.则,故A正确;
B中,因为,所以.故,即,故B错误;
C中,因为,又,则,所以,故C正确;
D中,因为,根据在上单调递减,可得,而在定义域上单调递增,所以,故D错误.故选:AC.
10.ABC 【解析】由题意可得,每一个数位上的数字只能填0,1,每位数出现0,1是独立的,
因此,故A正确;
由于,故B正确;
∵,∴,故C正确,D错误.
故选:ABC.
11.BD 【解析】根据题意,A事件两瓶均为红色颜料,C事件为一瓶红色一瓶蓝色颜料,则事件A发生事件C必定不发生,
∴,故A,C不是独立事件,是互斥事件,故,故A,C错误;
若调出红色,需要两瓶颜料均为红色,若调出绿色,则需1瓶黄色和1瓶蓝色,此时调出红色和调出绿色不同时发生,故A,B为互斥事件,故B正确;
若B事件发生,,
若C事件发生,则甲有三种情况,分别为甲取两瓶黄色,甲取1瓶黄色和1瓶红色或蓝色,甲取1瓶红色1瓶蓝色,
则,故D正确.
故选:BD.
12.ACD 【解析】A.因为,所以令得,所以,A符合题意;
B.由当恒成立,令,则,由为区间上的“非减函数”,则,所以,则,B不符合题意;
C.,而,所以,
由,又,则,则,C符合题意;
当时,,
令,则,
则,即,D符合题意.
故选:ACD.
三、填空题(本大题共4小题,每小题5分,共20分.)
13.6 【解析】由已知得,当且仅当,即时取等号.
即,
令,则且,
得,即的最小值为6.
14. 【解析】因为函数的值域为,
所以,
解不等式得或.
15.34 【解析】令,得;
令,得;
二项式的通项公式为,
则,
所以.
16. 【解析】由本不等式,,故只需要即可,
即对于任意的恒成立,
等价于对任意的,或.
当时,由于,原式可变形为,记,
求导可知函数在上递减,在上递增.
于是在上递增,此时;
当时,由于,原式可变形为,记,
根据对勾函数性质在上递减,在上递增,
于是在上递减在上递增,
当,,注意到,故当时,,故.
综上,.
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.)
17.【解析】(1)当时,,
令,则在上单调觉增,
所以的值域为.
(2)由题可知,在上恒成立.
,
又在上单调递增.
所以,因此,
解得,
又为整数,所以或1.
18.【解析】(1)恒成立等价于,
当时,,对一切实数x不恒成立,则,当时,开口向下,对不恒成立.
所以此时必有解得,
所以实数a的取值范围是.
(2)依题意,因为,则,
当时,,解得;
当时,,解得或;
当时,,解得或,
所以,当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为.
19.【解析】(1)取的中点D,连接,
因为D,E分别为的中点,所以,
又因为,所以,
因为D,F分别为的中点,所以,
又因为为直三棱柱,所以,
所以,
因为平面平面,
所以平面,因为平面,所以.
(2)设,以C为原点,分别为x,y,z轴建立如图空间直角坐标系,
因为,则,
,
设平面的一个法向量,
则即取,
为平面的一个法向量,平面与平面所成锐二面角的余弦值为,
所以,解得,
由(1)知即直线与平面所成的角,,
,所以直线与平面所成的角的正弦值为.
20.【解析】(1)由,得,令,即,
最小三东法公式得:,
∵,
∴,
∴,
则,
故y关于x的回归方程为.
(2)∵,所以,
∴,解得,
引入云计算后,,所以,
若保持单件产品的成本不变,则,
∴,
若保持产品质量不变(即误差的概率分布不变),
则,∴,即单件产品降价元.
21.【解析】(1)“自由式滑雪”参与人数超过40人的学校有4所,则X的可能取值为0,1,2,3.
.
所以X的分布列为:
X 0 1 2 3
P
所以.
(2)由题可知,
参与“自由式滑雪”的人数超过40人的学校,且参加“单板滑雪”的人数不超过30人的学校为C、G,
参与“自由式滑雪”的人数超过40人,且参加“单板滑雪”的人数超过30人的学校为D、I,
参与“自由式滑雪”的人数不超过40人,且参加“单板滑雪”的人数超过30人的学校为A、B、E、H,
参与“自由式滑雪”的人数不超过40人,且参加“单板滑雪”的人数不超过30人的学校为F、J,
设事件A为“从这10所学校中抽3所学校恰有一个参与‘自由式滑雪?的人数超过40人”.
事件B为“从这10所学校中抽3所学校恰有一个参与‘单板滑雪’的人数超过30人”.
则.
若“自由式滑雪”的人数超过40人和“单板滑雪”人数超过30人为同一个学校,则有种情况,
若“自由式滑雪”的人数超过40人和“单板滑雪”人数超过30人非同一个学校,则有种情况,,
所以.
(3)由题意可得小明同学在一轮测试中为“优秀”的概率为:.
所以小明在n轮测试中获得“优秀”的次数Y满足,由,得.
所以理论上至少要进行12轮测试.
22.【解析】函数,由,可得,
.即为奇函数,
且时递减,可得在递减,且的值域为,
不等式,即为,则,
即,即为,解得,则原不等式的解集为.
(2)函数,
若存在,使得成立,
当的值域为,
当时,在递减,可得的值域为,
由题意可得和的值域需要存在交集,即有,即;
若,则在递增,可得的值域为,
可得和的值域不存在交集,故不符合题意.
综上可得a的范围是.
(3),
(ⅰ)当,
则在上单调递减,
∴,
①若,即时,存在上界,
②若,即时,存在上界;
(ⅱ)当时,
①若时,在上单调递增,,存在上界;
②若时,在上单调递增,,故不存在上界;
③若时,在上单调递增,在上单调递增,,故不存在上界;
④若,在上单调递增,,故不存在上界;
⑤若在上单调递增,,而,故存在上界.
综上所述,当时,存在上界,
当时,不存在上界,
当时,存在上界,
当时,存在上界,
当时,存在上界.
数学
时量:120分钟 满分:150分
得分:___________
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合,则( )
A. B. C. D.
2.设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件
3.若函数的值域为,则函数的大致图象是( )
A. B. C. D.
4.一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员先将的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.你认为顾客购得的黄金
附:依据力矩平衡原理,天平平衡时有,其中分别为左右盘中物体质量,分别为左右横梁臂长.( )
A.等于 B.小于 C.大于 D.不确定
5.天文学中常用“星等”来衡量天空中星体的明亮程度,一个望远镜能看到的最暗的天体星等称为这个望远镜的“极限星等”.在一定条件下,望远镜的极限星等M与其口径D(即物镜的直径,单位:)近似满足关系式,例如:口径的望远镜的极限星等约为10.3.则口径的望远镜的极限星等约为( )
A.12.8 B.13.3 C.13.8 D.14.3
6.2023年3月,某校A,B,C,D,E,F六名同学参加了中学生地球科学奥林匹克竞赛,均在比赛中取得优异成绩,现这6名同学和他们的主教练共7人站成一排合影留念,则主教练和A站在两端,B、C相邻,B、D不相邻的排法种数为( )
A.36 B.48 C.56 D.72
7.已知,则( )
A. B. C. D.
8.记设函数,若函数恰有三个零点,则实数m的取值范围的是( )
A. B.
C. D.
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对的得2分,有选错的得0分.)
9.若,则下列不等式正确的是( )
A. B. C. D.
10.某计算机程序每运行一次都随机出现一个n位二进制数,其中,若在A的各数位上出现0和1的概率均为且相互独立,记,则当程序运行一次时( )
A.
B.
C.X的数学期望
D.X的方差
11.红黄蓝被称为三原色,选取任意几种颜色调配,可以调配出其他颜色.已知同一种颜色混合颜色不变,等量的红色加黄色调配出橙色;等量的红色加蓝色调配出紫色;等量的黄色加蓝色调配出绿色.现有红黄蓝彩色颜料各两瓶,甲从六瓶中任取两瓶颜料,乙再从余下四瓶中任取两瓶颜料,两人分别进行等量调配,A表示事件“甲调配出红色”;B表示事件“甲调配出绿色”;C表示事件“乙调配出紫色”,则下列说法正确的是( )
A.事件A与事件C是独立事件 B.事件A与事件B是互斥事件
C. D.
12.对于定义在区间D上的函数,若满足:且,都有,则称函数为区间D上的“非减函数”.若为区间上的“非减函数”,且,,又当时,恒成立,下列命题中正确的有( )
A. B.
C. D.
三、填空题(本大题共4小题,每小题5分,共20分.)
13.已知,则的最小值为_____________.
14.已知函数的值域为,则k的取值范围是____________.
15.已知,则___________.(用数字作答)
16.若对于任意实数x及,均有,则实数a的取值范围是_____________.
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.)
17.(本小题满分10分)
已知关于x的函数,其中.
(1)当时,求的值域;
(2)若当时,函数的图象总在直线的上方,为整数,求的值.
18.(本小题满分12分)
已知函数.
(1)若不等式对于一切实数x恒成立,求实数a的取值范围;
(2)若,解关于x的不等式.
19.(本小题满分12分)
如图,在直三棱柱中,E,F分别是棱的中点,.
(1)证明:;
(2)若,平面与平面所成锐二面角的余弦值为,求直线与平面所成角的正弦值.
20.(本小题满分12分)
云计算是信息技术发展的集中体现,近年来,我国云计算市场规模持续增长.从中国信息通信研究院发布的《云计算白皮书(2022年)》可知,我国2017年至2021年云计算市场规模数据统计表如下:
年份 2017年 2018年 2019年 2020年 2021年
年份代码x 1 2 3 4 5
云计算市场规模y/亿元 692 962 1334 2091 3229
经计算得:.
(1)根据以上数据,建立y关于x的回归方程(e为自然对数的底数);
(2)云计算为企业降低生产成本、提升产品质量提供了强大助推力.某企业未引入云计算前,单件产品尺寸与标准品尺寸的误差,其中m为单件产品的成本(单位:元),且;引入云计算后,单件产品尺寸与标准品尺寸的误差,若保持单件产品的成本不变,则将会变成多少?若保持产品质量不变(即误差的概率分布不变),则单件产品的成本将会下降多少?
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为.
若,则.
21.(本小题满分12分)
2022年冬季奥林匹克运动会主办城市是北京,北京成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市.为迎接冬奥会的到来,某地很多中小学开展了模拟冬奥会
赛事的活动,为了深入了解学生在“自由式滑雪”和“单板滑雪”两项活动的参与情况,在该地随机选取了10所学校进行研究,得到如图数据:
(1)“自由式滑雪”参与人数超过40人的学校可以作为“基地学校”,现在从这10所学校中随机选出3所,记X为可作为“基地学校”的学校个数,求X的分布列和数学期望;
(2)在这10所学校中随机选取3所来调查研究,求在抽到学校中恰有一所参与“自由式滑雪”超过40人的条件下,抽到学校中恰有一所学校“单板滑雪”超过30人的概率;
(3)现在有一个“单板滑雪”集训营,对“滑行、转弯、停止”这3个动作技巧进行集训,且在集训中进行了多轮测试.规定:在一轮测试中,这3个动作中至少有2个动作达到“优秀”,则该轮测试记为“优秀”.在集训测试中,小明同学3个动作中每个动作达到“优秀”的概率均为,每个动作互不影响且每轮测试互不影响.如果小明同学在集训测试中要想获得“优秀”的次数的平均值达到3次,那么理论上至
少要进行多少轮测试?
22.(本小题满分12分)
已知函数,函数.函数.
(1)求不等式的解集;
(2)若存在,使得成立,求实数a的取值范围;
(3)定义在I上的函数,如果满足:对任意,存在常数,都有成立,则称函数是I上的有界函数,其中M称为函数在I的上界.讨论函数在上是否存在上界?若存在,求出M的取值范围;若不存在,请说明理由.
数学参考答案
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
题号 1 2 3 4 5 6 7 8
答案 C B A C B D A B
1.C 【解析】由得:,而,
所以.
故选:C.
2.B 【解析】由可得,即,可等价变形为:,即或,显然“或”是“”的必要不充分条件.
故选:B.
3.A 【解析】∵,且的值域为,∴,
当时,在上是增函数.
又函数的图象关于y轴对称,
所以的大致图象应为选项A.
故选:A.
4.C 【解析】设天平左臂长,右臂长,且,
设天平右盘有克黄金,天平左盘有克黄金,
所以
所以.
故选:C.
5.B 【解析】由题意,∴,∴.
∴.
故选:B.
6.D 【解析】分2步进行分析:
①主教练和A站在两端,有种情况;
②中间5人分2种情况讨论:
若B、C相邻且与D相邻,有种安排方法;
若B、C相邻且不与D相邻,有种安排方法,
则中间5人有种安排方法,则共有种不同的安排方法.故选:D.
7.A 【解析】;
设,因为函数在上递增,,,即,由零点存在定理可知;
设函数,易知在上递减,,即,由零点存在定理可知.即.故选:A.
8.B 【解析】设,
则函数在上递增,且,且函数至多有两个零点,
当时,,
若函数在上有零点,则在上有零点,不妨设零,点为,则,
此时,则,与题意矛盾,
故函数在上无零点.
二次函数图象对称销为直线,函数在上有两个零点,所以
解得故选:B.
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对的得2分,有选错的得0分.)
题号 9 10 11 12
答案 AC ABC BD ACD
9.AC 【解析】由,可知.
A中,因为.所以.则,故A正确;
B中,因为,所以.故,即,故B错误;
C中,因为,又,则,所以,故C正确;
D中,因为,根据在上单调递减,可得,而在定义域上单调递增,所以,故D错误.故选:AC.
10.ABC 【解析】由题意可得,每一个数位上的数字只能填0,1,每位数出现0,1是独立的,
因此,故A正确;
由于,故B正确;
∵,∴,故C正确,D错误.
故选:ABC.
11.BD 【解析】根据题意,A事件两瓶均为红色颜料,C事件为一瓶红色一瓶蓝色颜料,则事件A发生事件C必定不发生,
∴,故A,C不是独立事件,是互斥事件,故,故A,C错误;
若调出红色,需要两瓶颜料均为红色,若调出绿色,则需1瓶黄色和1瓶蓝色,此时调出红色和调出绿色不同时发生,故A,B为互斥事件,故B正确;
若B事件发生,,
若C事件发生,则甲有三种情况,分别为甲取两瓶黄色,甲取1瓶黄色和1瓶红色或蓝色,甲取1瓶红色1瓶蓝色,
则,故D正确.
故选:BD.
12.ACD 【解析】A.因为,所以令得,所以,A符合题意;
B.由当恒成立,令,则,由为区间上的“非减函数”,则,所以,则,B不符合题意;
C.,而,所以,
由,又,则,则,C符合题意;
当时,,
令,则,
则,即,D符合题意.
故选:ACD.
三、填空题(本大题共4小题,每小题5分,共20分.)
13.6 【解析】由已知得,当且仅当,即时取等号.
即,
令,则且,
得,即的最小值为6.
14. 【解析】因为函数的值域为,
所以,
解不等式得或.
15.34 【解析】令,得;
令,得;
二项式的通项公式为,
则,
所以.
16. 【解析】由本不等式,,故只需要即可,
即对于任意的恒成立,
等价于对任意的,或.
当时,由于,原式可变形为,记,
求导可知函数在上递减,在上递增.
于是在上递增,此时;
当时,由于,原式可变形为,记,
根据对勾函数性质在上递减,在上递增,
于是在上递减在上递增,
当,,注意到,故当时,,故.
综上,.
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.)
17.【解析】(1)当时,,
令,则在上单调觉增,
所以的值域为.
(2)由题可知,在上恒成立.
,
又在上单调递增.
所以,因此,
解得,
又为整数,所以或1.
18.【解析】(1)恒成立等价于,
当时,,对一切实数x不恒成立,则,当时,开口向下,对不恒成立.
所以此时必有解得,
所以实数a的取值范围是.
(2)依题意,因为,则,
当时,,解得;
当时,,解得或;
当时,,解得或,
所以,当时,原不等式的解集为;当时,原不等式的解集为;
当时,原不等式的解集为.
19.【解析】(1)取的中点D,连接,
因为D,E分别为的中点,所以,
又因为,所以,
因为D,F分别为的中点,所以,
又因为为直三棱柱,所以,
所以,
因为平面平面,
所以平面,因为平面,所以.
(2)设,以C为原点,分别为x,y,z轴建立如图空间直角坐标系,
因为,则,
,
设平面的一个法向量,
则即取,
为平面的一个法向量,平面与平面所成锐二面角的余弦值为,
所以,解得,
由(1)知即直线与平面所成的角,,
,所以直线与平面所成的角的正弦值为.
20.【解析】(1)由,得,令,即,
最小三东法公式得:,
∵,
∴,
∴,
则,
故y关于x的回归方程为.
(2)∵,所以,
∴,解得,
引入云计算后,,所以,
若保持单件产品的成本不变,则,
∴,
若保持产品质量不变(即误差的概率分布不变),
则,∴,即单件产品降价元.
21.【解析】(1)“自由式滑雪”参与人数超过40人的学校有4所,则X的可能取值为0,1,2,3.
.
所以X的分布列为:
X 0 1 2 3
P
所以.
(2)由题可知,
参与“自由式滑雪”的人数超过40人的学校,且参加“单板滑雪”的人数不超过30人的学校为C、G,
参与“自由式滑雪”的人数超过40人,且参加“单板滑雪”的人数超过30人的学校为D、I,
参与“自由式滑雪”的人数不超过40人,且参加“单板滑雪”的人数超过30人的学校为A、B、E、H,
参与“自由式滑雪”的人数不超过40人,且参加“单板滑雪”的人数不超过30人的学校为F、J,
设事件A为“从这10所学校中抽3所学校恰有一个参与‘自由式滑雪?的人数超过40人”.
事件B为“从这10所学校中抽3所学校恰有一个参与‘单板滑雪’的人数超过30人”.
则.
若“自由式滑雪”的人数超过40人和“单板滑雪”人数超过30人为同一个学校,则有种情况,
若“自由式滑雪”的人数超过40人和“单板滑雪”人数超过30人非同一个学校,则有种情况,,
所以.
(3)由题意可得小明同学在一轮测试中为“优秀”的概率为:.
所以小明在n轮测试中获得“优秀”的次数Y满足,由,得.
所以理论上至少要进行12轮测试.
22.【解析】函数,由,可得,
.即为奇函数,
且时递减,可得在递减,且的值域为,
不等式,即为,则,
即,即为,解得,则原不等式的解集为.
(2)函数,
若存在,使得成立,
当的值域为,
当时,在递减,可得的值域为,
由题意可得和的值域需要存在交集,即有,即;
若,则在递增,可得的值域为,
可得和的值域不存在交集,故不符合题意.
综上可得a的范围是.
(3),
(ⅰ)当,
则在上单调递减,
∴,
①若,即时,存在上界,
②若,即时,存在上界;
(ⅱ)当时,
①若时,在上单调递增,,存在上界;
②若时,在上单调递增,,故不存在上界;
③若时,在上单调递增,在上单调递增,,故不存在上界;
④若,在上单调递增,,故不存在上界;
⑤若在上单调递增,,而,故存在上界.
综上所述,当时,存在上界,
当时,不存在上界,
当时,存在上界,
当时,存在上界,
当时,存在上界.
同课章节目录
