3.2圆锥同步练习六年级数学下册(人教版)(含解析)
文档属性
| 名称 | 3.2圆锥同步练习六年级数学下册(人教版)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 303.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-23 00:00:00 | ||
图片预览




文档简介
3.2圆锥 同步练习 六年级数学下册(人教版)含答案
一、填空题
1.圆柱有( )条高,圆锥有( )条高。
2.一般情况下,圆柱的侧面展开后是一个( )形,圆锥侧面展开是一个( )形。
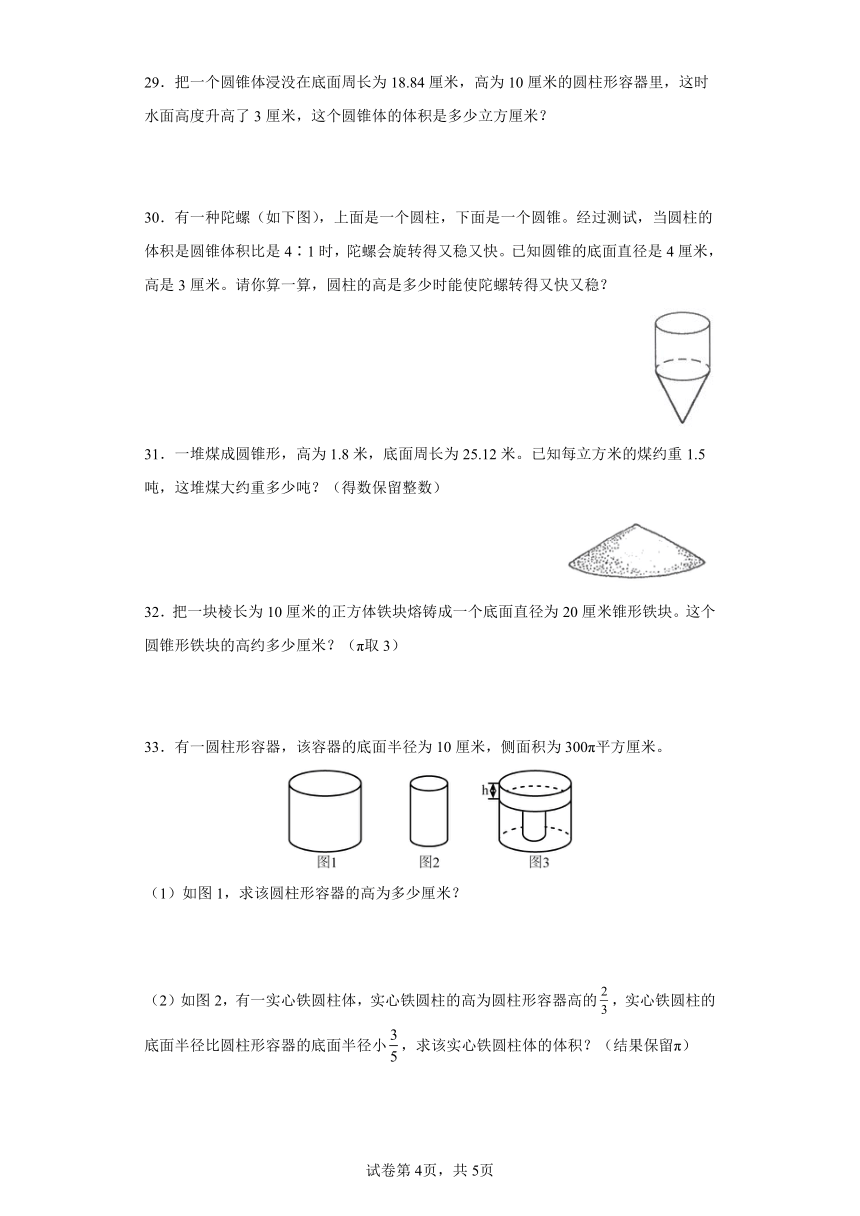
3.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
(第3题) (第4题)
4.如图,将下面这个圆柱形木桩切削成一个最大的圆锥,削成后的圆锥的体积是( )立方分米。
5.一个圆锥的体积是36立方分米,它的底面积是18平方分米,它的高是( )分米。
6.一个圆柱和一个圆锥的体积相等,底面积也相等,如果圆锥的高是12cm,则圆柱的高是( )cm。
7.一个圆锥形沙堆,底面积是12.56m2,高是4.5m。用这堆沙在10m宽的公路上铺4cm厚的路面,能铺( )m。
8.一个圆柱的底面半径是6dm,高是3dm,它的侧面积是( )dm2,表面积是( )dm2,体积是( )dm3,与它等底等高的圆锥的体积是( )dm3。
9.如图,将一张三角形纸按照1∶3缩小。
(1)求缩放前后两张三角形纸的面积比:S①∶S②=( )∶( )。
(2)将两张三角形纸(阴影部分)分别绕AC、A1C1旋转后会得到两个圆锥,求它们的体积比:V①∶V②=( )∶( )。
二、选择题
10.将直角三角形沿一条直角边旋转,得到的立体图形是( )。
A. B. C.
11.在如图中,旋转后可以得到的是图( )。
A. B. C.
12.把一个底面直径6cm,高9cm的圆锥形木块,沿底面直径切成完全相同的两块后,表面积比原来增加了( )cm2。
A.54 B.108 C.27
13.将一个圆锥沿着它的高平均切成两块,切面一定是一个( )。
A.长方形 B.圆形 C.等腰三角形
14.一个圆柱和一个圆锥等底等高,它们的体积差是24dm3,圆锥的体积是( )。
A.36dm3 B.12dm3 C.24dm3
15.一种容器(如图),将容器倒过来后,水面的高度是( )cm。
A.5
B.7
C.9
16.一个圆锥的底面周长是18.84厘米,高是5厘米。它的体积是( )立方厘米。
A.141.3 B.47.1 C.70.65
17.下列说法:①一个圆的周长总是直径的3.14倍;②甲数除以乙数(不等于0)等于甲数乘乙数的倒数:③如果圆柱的体积是圆锥的体积的3倍,那么圆柱与圆锥的高一定相等:④比的前项和比的后项同时乘以一个相同的数,比值不变。其中正确的有( )。
A.1个 B.2个 C.3个
18.一个圆柱的体积是141.3立方米,与它等底等高的圆锥的体积是( )。
A.47.1立方米 B.141.3立方米 C.282.6立方米
三、判断题
19.圆锥的高不变,底面直径扩大到原来的2倍,它的体积就扩大到原来的4倍。( )
20.底面半径越大的圆锥,底面积就越大,体积也就越大。( )
21.如果圆柱的体积等于圆锥体积的3倍,那么它们一定等底等高。( )
22.等底等高的圆柱和圆锥,圆锥的体积比圆柱小。( )
23.等腰三角形,绕任意一边旋转一周都不能形成圆锥。( )
24.不论沿着直角三角形的哪一条边旋转一周,都可以得到圆锥。( )
四、计算
25.计算出下面图形围绕虚线旋转一周后形成的立体图形的体积。(单位:厘米)
26.计算下面圆锥的体积。
五、解答题
27.小丽想准确量出圆锥的高,请你结合自己的经验说说自己的测量方法。(可以写出来,也可以画出来)
28.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5米,高是2.4米。这种圆锥形帐篷占地面积是多少?
29.把一个圆锥体浸没在底面周长为18.84厘米,高为10厘米的圆柱形容器里,这时水面高度升高了3厘米,这个圆锥体的体积是多少立方厘米?
30.有一种陀螺(如下图),上面是一个圆柱,下面是一个圆锥。经过测试,当圆柱的体积是圆锥体积比是4∶1时,陀螺会旋转得又稳又快。已知圆锥的底面直径是4厘米,高是3厘米。请你算一算,圆柱的高是多少时能使陀螺转得又快又稳?
31.一堆煤成圆锥形,高为1.8米,底面周长为25.12米。已知每立方米的煤约重1.5吨,这堆煤大约重多少吨?(得数保留整数)
32.把一块棱长为10厘米的正方体铁块熔铸成一个底面直径为20厘米锥形铁块。这个圆锥形铁块的高约多少厘米?(π取3)
33.有一圆柱形容器,该容器的底面半径为10厘米,侧面积为300π平方厘米。
(1)如图1,求该圆柱形容器的高为多少厘米?
(2)如图2,有一实心铁圆柱体,实心铁圆柱的高为圆柱形容器高的,实心铁圆柱的底面半径比圆柱形容器的底面半径小,求该实心铁圆柱体的体积?(结果保留π)
(3)在(2)的条件下,现有底面半径为5厘米,高为12厘米的实心冰圆锥若干,水变成冰体积会增加,现将实心铁圆柱体放入圆柱形容器,如图3,将冰圆锥化成的水注入圆柱形容器内,注入的水将实心铁圆柱体全部浸没。求至少需要多少个冰圆锥(整数个)?并求此时水面与容器口的距离h为多少厘米?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 无数 1
【分析】圆柱的两个底面之间的距离叫做高;圆柱的高有无数条。
从圆锥的顶点到底面圆心的距离是圆锥的高。
【详解】如图:
圆柱有无数条高,圆锥有1条高。
2. 长方 扇
【分析】根据圆柱的特征,它的上、下是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;如果圆柱体的底面周长和高相等时,侧面展开是正方形,据此解答。
【详解】由分析可得:一般情况下,圆柱的侧面展开后是一个长方形,圆锥侧面展开是一个扇形。
3. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
4.3.14
【分析】如果将圆柱形木桩切削成一个最大的圆锥,则圆锥相当于圆柱的,圆锥的高相当于圆柱的高,圆锥的底面相当于圆柱的底面,根据圆锥的体积公式:V=πr2h,用3.14×(2÷2)2×3×即可求出圆锥的体积。
【详解】3.14×(2÷2)2×3×
=3.14×12×3×
=3.14×1×3×
=3.14(立方分米)
削成后的圆锥的体积是3.14立方分米。
5.6
【分析】根据圆锥的体积公式:V=Sh,那么h=V÷÷S,据出解答。
【详解】36÷÷18
=36×3÷18
=108÷18
=6(分米)
它的高是6分米。
6.4
【分析】根据等底等高圆锥的体积是圆柱体积的,已知圆锥和圆柱等底等体积,圆锥的高是12cm,那么圆柱的高是圆锥高的,由此解答。
【详解】12×=4(cm)
圆柱的高是4cm。
7.47.1
【分析】这堆沙的体积不变,根据圆锥的体积公式求出这堆沙的体积,再除以10,除以0.04,就是可铺的长,据此解答。
【详解】4cm=0.04m
×12.56×4.5÷10÷0.04
=×56.52÷10÷0.04
=18.84÷10÷0.04
=1.884÷0.04
=47.1(m)
能铺47.1m。
8. 113.04 339.12 339.12 113.04
【分析】根据圆柱的侧面积公式:S=2πrh,圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【详解】圆柱的侧面积:2×3.14×6×3
=6.28×6×3
=37.68×3
=113.04(dm2)
圆柱的表面积:113.04+3.14×62×2
=113.04+113.04×2
=113.04+226.08
=339.12(dm2)
圆柱的体积:3.14×62×3
=113.04×3
=339.12(dm3)
圆锥的体积:339.12×=113.04(dm3)
9.(1) 9 1 (2) 27 1
【分析】(1)根据三角形的面积=底×高÷2,计算出两个图形的面积,根据比的意义写出比,化简比即可;
(2)根据题意,图①旋转得到的圆锥的底面半径是30cm,高是40cm;图②旋转得到的圆锥的底面半径是(30÷3)cm,高是(40÷3)cm,根据公式:圆锥的体积=底面积×高×计算出结果,根据比的意义写出比,化简比即可。
【详解】(1)图①的面积:
30×40÷2
=1200÷2
=600(cm2)
图②的面积:
(30÷3)×(40÷3)÷2
=10××
=(cm2)
所以,S①∶S②=600∶=9∶1
(2)V①:
30×30×π×40×
=900××π×40
=300×40×π
=12000π(cm3)
V②:
(30÷3)×(30÷3)×π×(40÷3)×
=10×10×π××
=100π×
=π(cm3)
12000π∶π=27∶1
所以V①∶V②=27∶1
10.C
【分析】根据对圆柱和圆锥的认识,长方形旋转一周得到一个圆柱,直角三角形旋转一周得到一个圆锥。据此解题。
【详解】将直角三角形ABC,绕直角边AC旋转一周,便形成了圆锥。其中AC是圆锥的高;CB是圆锥底面的半径。
如图:
故答案为:C
11.C
【分析】根据面动成体判断出各选项中旋转得到立体图形即可得解。
【详解】A.以直角三角形的一条直角边为轴旋转,可以得到一个圆锥;
B.以长方形的一条边为轴旋转,可以得到一个圆柱;
C.以直角梯形的下底为轴旋转,可以得到一个圆柱和一个圆锥的组合图形。
故答案为:C
12.A
【分析】根据题意,把圆锥形木块沿底面直径切成完全相同的两块后,表面积比原来增加两个切面的面积,切面是一个底等于圆锥的底面直径,高等于圆锥的高的三角形;根据三角形的面积=底×高÷2,求出一个切面的面积,再乘2,即是增加的表面积。
【详解】6×9÷2×2
=54÷2×2
=54(cm2)
表面积比原来增加了54cm2。
故答案为:A
13.C
【分析】以直角三角形的一条直角边所在的直线为轴旋转一周,就可以得到一个圆锥,把圆锥沿着高平均切成两块之后,切面是一个以圆锥的高为高的等腰三角形,据此解答。
【详解】
如图所示,将一个圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
故答案为:C
14.B
【分析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积等于圆锥体积的3倍,即把圆锥的体积看作l份,圆柱的体积是3份,份数相差(3-1)份;用等底等高的圆柱和圆锥的体积之差除以份数差,求出一份数,即是圆锥的体积。
【详解】24÷(3-1)
=24÷2
=12(dm3)
圆锥的体积是12dm3。
故答案为:B
15.C
【分析】圆柱和圆锥的底面积相等,圆锥的高度为15cm,圆柱的高度为(19-15)cm,容器倒置后,圆锥里面的水在圆柱里面的高度为圆锥高度的,最后加上原来圆柱里面水的高度就是倒置后的水面高度,据此解答。
【详解】15×+(19-15)
=5+4
=9(cm)
水面的高度是9cm。
故答案为:C
16.B
【分析】已知圆锥的底面周长是18.84厘米,根据圆周长公式:C=2πr,用18.84÷3.14÷2即可求出圆锥的底面半径,再根据圆锥的体积公式:V=πr2h求出圆锥的体积。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×5×
=3.14×9×5×
=47.1(立方厘米)
圆锥的体积是47.1立方厘米。
故答案为:B
17.A
【分析】利用圆的周长公式、比的定义及性质、圆的性质分别判断后即可确定正确的选项。
【详解】①一个圆的周长总是它的直径的π倍,故①错误;
②甲数除以乙数(不等于0)等于甲数乘乙数的倒数,说法正确,故②正确;
③圆锥以及圆柱的体积还与底面积有关,说法错误,故③错误;
④比的前项和比的后项同时乘或除以一个相同的数(不为0),比值不变,原说法错误,故④错误;
正确的有1个。
故答案为:A
18.A
【分析】等底等高的圆柱的体积是圆锥的体积的3倍,所以用圆柱的体积除以3即可求出圆锥的体积,由此即可解答。
【详解】141.3÷3=47.1(立方米)
一个圆柱的体积是141.3立方米,与它等底等高的圆锥的体积是47.1立方米。
故答案为:A
19.√
【分析】根据:圆锥的体积=底面积×高×,底面积=π×r2,若底面直径扩大到原来的a倍,高不变,那么底面半径也扩大到原来的a倍,则圆锥的体积会扩大到原来的a2倍,据此判断即可。
【详解】根据分析,2×2=4
圆锥的高不变,底面直径扩大到原来的2倍,它的体积就扩大到原来的4倍,说法正确;
故答案为:√
20.×
【分析】根据圆锥的体积计算公式“V=”得出:圆锥的体积不但与圆锥的底面半径有关,还跟圆锥的高有关;只有在高相同的情况下,圆锥的底面半径越大,它的体积就越大;不能只凭一种情况,就下结论。
【详解】根据分析得,当高一定的情况下,底面半径越大的圆锥,底面积就越大,体积也就越大。所以原题的说法是错误的。
故答案为:×
21.×
【分析】圆柱的体积等于圆锥体积的3倍,根据圆柱的体积公式:V柱=πr2h,圆锥的体积公式:V锥=πr2h,圆柱的体积和圆锥的体积由底面半径和高确定,所以两个条件都未知,无法判断它们是否等底等高。
【详解】根据题意可知,如果圆柱的体积等于圆锥体积的3倍,那么它们不一定等底等高,原题干说法错误。
故答案为:×
22.×
【分析】因为等底等高的圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,根据求一个数比另一个少几分之几,用除法解答。
【详解】把圆柱的体积看作单位“1”,
(1-)÷1
=÷1
=
即圆锥的体积比圆柱小。
故答案为:×
23.×
【分析】以直角三角形的一条直角边为轴旋转一周可得到一个圆锥,据此判断。
【详解】等腰三角形也是直角三角形时,以直角三角形的一条直角边为轴旋转一周可形成一个圆锥。
原题说法错误。
故答案为:×
24.×
【分析】根据旋转的特点,以直角三角形任意一条直角边旋转一周,都可以得到一个圆锥体。据此解答。
【详解】任何一个直角三角形以任意一条直角边为轴旋转一周,都可以得到一个圆锥,而不是任意一边,当它以斜边旋转一周时得到的就不是圆锥体了,本题结论是错误的。
故答案为:×
25.37.68立方厘米
【分析】根据题意,图形围绕虚线旋转一周后形成的立体图形是底面半径为3厘米,高为4厘米的圆锥,根据公式:圆锥的体积=底面积×高×,底面积=πr2,将数据代入计算即可。
【详解】3.14×32×4×
=28.25×4×
=113.04×
=37.68(立方厘米)
26.(1)47.1立方厘米;(2)37.68立方分米
【分析】圆锥的体积= ×底面积×高= πr h,半径=直径÷2,代入公式计算即可。
【详解】(1)6÷2=3(厘米)
×3.14×3 ×5
=9.42×5
=47.1(立方厘米)
(2)3.14×2 ×9×
=12.56×9×
=37.68(立方分米)
27.【分析】根据测量圆锥高的方法进行解答即可。
【详解】测量圆锥高的方法:
①先把圆锥的底面放平
②用一块平板水平地放在圆锥的顶点上面
③竖直地量出平板和底面之间的距离
28.19.625平方米
【分析】求圆锥的占地面积,就是求直径是5米的圆的面积,根据圆的面积=πr2,代入数据,即可解答。
【详解】3.14×(5÷2)2
=3.14×2.52
=19.625(平方米)
这种圆锥形帐篷占地面积是19.625平方米。
29.84.78立方厘米
【分析】根据圆柱的底面半径r=C÷π÷2,先求出圆柱形容器的底面半径;把圆锥体浸没在装有水的圆柱形容器里,水面升了3厘米,那么水面升高部分的体积等于这个圆锥的体积;根据圆柱的体积公式V=πr2h,代入数据计算即可。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×3
=3.14×9×3
=3.14×27
=84.78(立方厘米)
答:这个圆锥体的体积是84.78立方厘米。
30.4厘米
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥的体积,圆柱的体积是圆锥体积的4倍,把数据代入公式求出圆柱的体积,再根据圆柱的体积公式:V=πr2h,那么h=V÷πr2,把数据代入公式解答。
【详解】×3.14×(4÷2)2×3×4÷[3.14×(4÷2)2]
=×3.14×(4÷2)2×3×4÷[3.14×4]
=×3.14×4×3×4÷[3.14×4]
=×12.56×3×4÷12.56
=×37.68×4÷12.56
=12.56×4÷12.56
=50.24÷12.56
=4(厘米)
答:圆柱的高是4厘米时能使陀螺转得又快又稳。
31.45吨
【分析】此题需要先利用圆的周长公式求出这堆煤的底面半径,再利用圆锥的体积V=Sh,求出这堆煤的体积,进而用这堆煤的体积乘每立方米的煤的重量,就是这堆煤的总重量。
【详解】底面半径:25.12÷(2×3.14)
=25.12÷6.28
=4(米)
这堆煤的体积:
×3.14×42×1.8
=×3.14×16×1.8
=×50.24×1.8
=×90.432
=30.144(立方米)
这堆煤的重量:30.144×1.5≈45(吨)
答:这堆煤共重45吨。
32.10厘米
【分析】先求出正方体的体积,正方体的体积=棱长×棱长×棱长,因为将正方体铁块熔铸成圆锥形铁块,所以体积相等;圆锥的体积=×底面积×高,则圆锥的高=圆锥的体积÷底面积÷,圆锥的底面是一个圆,圆的面积=πr2,代入公式计算即可。
【详解】10×10×10=1000(立方厘米)
3×(20÷2)2
=3×100
=300(平方厘米)
1000÷300÷
=1000÷300×3
=10(厘米)
答:圆锥形铁块的高约是10厘米。
33.(1)15厘米
(2)160π立方厘米
(3)10个;4.4厘米
【分析】(1)先根据圆的底面周长公式C=2πr,求出圆柱的底面周长;再根据圆柱的侧面积公式S侧=Ch可知,圆柱的高h=S侧÷C,代入数据计算即可求出圆柱形容器的高。
(2)根据“实心铁圆柱的高为圆柱形容器高的”,把圆柱形容器的高看作单位“1”,单位“1”已知,用乘法求出实心铁圆柱的高;
根据“实心铁圆柱的底面半径比圆柱形容器的底面半径小”,把圆柱形容器的底面半径看作单位“1”,单位“1”已知,用乘法求出实心铁圆柱的底面半径;
然后根据圆柱的体积公式V=πr2h,求出这个实心铁圆柱的体积。
(3)已知实心冰圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,求出一个实心冰圆锥的体积;
已知水变成冰体积会增加,即冰的体积比水的体积增加,把水的体积看作单位“1”,冰的体积是水体积的(1+),单位“1”未知,用除法计算,求出一个实心冰圆锥化成水后的体积;
现将实心铁圆柱体放入圆柱形容器,水要浸没实心铁圆柱体,水的高度至少等于实心铁圆柱体的高10厘米,根据圆柱的体积公式V=πr2h,求出水和实心铁圆柱体的总体积;再减去实心铁圆柱体的体积,就是至少需要水的体积;用水的体积除以一个实心冰圆锥的体积,即可求出至少需要实心冰圆锥的个数,得数用进一法取整数。
用实心铁圆柱体的体积加上10个实心冰圆锥的体积,除以圆柱形容器的底面积,求出此时水面的高度,再用圆柱形容器的高减去水面的高度,即可求出此时水面与容器口的距离。
【详解】(1)圆柱的底面周长:2×π×10=20π(厘米)
圆柱的高:300π÷20π=15(厘米)
答:该圆柱形容器的高为15厘米。
(2)实心铁圆柱的高:15×=10(厘米)
实心铁圆柱的底面半径:
10×(1-)
=10×
=4(厘米)
实心铁圆柱体的体积:
π×42×10
=π×16×10
=160π(立方厘米)
答:该实心铁圆柱体的体积是160π立方厘米。
(3)一个实心冰圆锥的体积:
×π×52×12
=×π×25×12
=100π(立方厘米)
一个实心冰圆锥化成水的体积:
100π÷(1+)
=100π÷
=100π×
=90π(立方厘米)
与实心铁圆柱体高相等的水的体积:
π×102×10
=π×100×10
=1000π(立方厘米)
恰好浸没实心铁圆柱体需要水:
1000π-160π=840π(立方厘米)
需要实心冰圆锥:
840π÷90π≈10(个)
水面的高度:
(160π+90π×10)÷(π×102)
=1060π÷100π
=10.6(厘米)
水面与容器口的距离:
15-10.6=4.4(厘米)
答:此时水面与容器口的距离h为4.4厘米。
答案第1页,共2页
答案第1页,共2页
一、填空题
1.圆柱有( )条高,圆锥有( )条高。
2.一般情况下,圆柱的侧面展开后是一个( )形,圆锥侧面展开是一个( )形。
3.如下图,将直角三角形ABC的直角边AB所在直线为轴旋转一周,所得到立体图形是( ),底面积为( )cm2。
(第3题) (第4题)
4.如图,将下面这个圆柱形木桩切削成一个最大的圆锥,削成后的圆锥的体积是( )立方分米。
5.一个圆锥的体积是36立方分米,它的底面积是18平方分米,它的高是( )分米。
6.一个圆柱和一个圆锥的体积相等,底面积也相等,如果圆锥的高是12cm,则圆柱的高是( )cm。
7.一个圆锥形沙堆,底面积是12.56m2,高是4.5m。用这堆沙在10m宽的公路上铺4cm厚的路面,能铺( )m。
8.一个圆柱的底面半径是6dm,高是3dm,它的侧面积是( )dm2,表面积是( )dm2,体积是( )dm3,与它等底等高的圆锥的体积是( )dm3。
9.如图,将一张三角形纸按照1∶3缩小。
(1)求缩放前后两张三角形纸的面积比:S①∶S②=( )∶( )。
(2)将两张三角形纸(阴影部分)分别绕AC、A1C1旋转后会得到两个圆锥,求它们的体积比:V①∶V②=( )∶( )。
二、选择题
10.将直角三角形沿一条直角边旋转,得到的立体图形是( )。
A. B. C.
11.在如图中,旋转后可以得到的是图( )。
A. B. C.
12.把一个底面直径6cm,高9cm的圆锥形木块,沿底面直径切成完全相同的两块后,表面积比原来增加了( )cm2。
A.54 B.108 C.27
13.将一个圆锥沿着它的高平均切成两块,切面一定是一个( )。
A.长方形 B.圆形 C.等腰三角形
14.一个圆柱和一个圆锥等底等高,它们的体积差是24dm3,圆锥的体积是( )。
A.36dm3 B.12dm3 C.24dm3
15.一种容器(如图),将容器倒过来后,水面的高度是( )cm。
A.5
B.7
C.9
16.一个圆锥的底面周长是18.84厘米,高是5厘米。它的体积是( )立方厘米。
A.141.3 B.47.1 C.70.65
17.下列说法:①一个圆的周长总是直径的3.14倍;②甲数除以乙数(不等于0)等于甲数乘乙数的倒数:③如果圆柱的体积是圆锥的体积的3倍,那么圆柱与圆锥的高一定相等:④比的前项和比的后项同时乘以一个相同的数,比值不变。其中正确的有( )。
A.1个 B.2个 C.3个
18.一个圆柱的体积是141.3立方米,与它等底等高的圆锥的体积是( )。
A.47.1立方米 B.141.3立方米 C.282.6立方米
三、判断题
19.圆锥的高不变,底面直径扩大到原来的2倍,它的体积就扩大到原来的4倍。( )
20.底面半径越大的圆锥,底面积就越大,体积也就越大。( )
21.如果圆柱的体积等于圆锥体积的3倍,那么它们一定等底等高。( )
22.等底等高的圆柱和圆锥,圆锥的体积比圆柱小。( )
23.等腰三角形,绕任意一边旋转一周都不能形成圆锥。( )
24.不论沿着直角三角形的哪一条边旋转一周,都可以得到圆锥。( )
四、计算
25.计算出下面图形围绕虚线旋转一周后形成的立体图形的体积。(单位:厘米)
26.计算下面圆锥的体积。
五、解答题
27.小丽想准确量出圆锥的高,请你结合自己的经验说说自己的测量方法。(可以写出来,也可以画出来)
28.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5米,高是2.4米。这种圆锥形帐篷占地面积是多少?
29.把一个圆锥体浸没在底面周长为18.84厘米,高为10厘米的圆柱形容器里,这时水面高度升高了3厘米,这个圆锥体的体积是多少立方厘米?
30.有一种陀螺(如下图),上面是一个圆柱,下面是一个圆锥。经过测试,当圆柱的体积是圆锥体积比是4∶1时,陀螺会旋转得又稳又快。已知圆锥的底面直径是4厘米,高是3厘米。请你算一算,圆柱的高是多少时能使陀螺转得又快又稳?
31.一堆煤成圆锥形,高为1.8米,底面周长为25.12米。已知每立方米的煤约重1.5吨,这堆煤大约重多少吨?(得数保留整数)
32.把一块棱长为10厘米的正方体铁块熔铸成一个底面直径为20厘米锥形铁块。这个圆锥形铁块的高约多少厘米?(π取3)
33.有一圆柱形容器,该容器的底面半径为10厘米,侧面积为300π平方厘米。
(1)如图1,求该圆柱形容器的高为多少厘米?
(2)如图2,有一实心铁圆柱体,实心铁圆柱的高为圆柱形容器高的,实心铁圆柱的底面半径比圆柱形容器的底面半径小,求该实心铁圆柱体的体积?(结果保留π)
(3)在(2)的条件下,现有底面半径为5厘米,高为12厘米的实心冰圆锥若干,水变成冰体积会增加,现将实心铁圆柱体放入圆柱形容器,如图3,将冰圆锥化成的水注入圆柱形容器内,注入的水将实心铁圆柱体全部浸没。求至少需要多少个冰圆锥(整数个)?并求此时水面与容器口的距离h为多少厘米?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 无数 1
【分析】圆柱的两个底面之间的距离叫做高;圆柱的高有无数条。
从圆锥的顶点到底面圆心的距离是圆锥的高。
【详解】如图:
圆柱有无数条高,圆锥有1条高。
2. 长方 扇
【分析】根据圆柱的特征,它的上、下是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高;如果圆柱体的底面周长和高相等时,侧面展开是正方形,据此解答。
【详解】由分析可得:一般情况下,圆柱的侧面展开后是一个长方形,圆锥侧面展开是一个扇形。
3. 圆锥 28.26
【分析】如果以三角形直角边AB所在直线为轴旋转一周,其旋转所形成图形是一个圆锥体,圆锥体底面半径为3cm的圆,根据圆的面积公式:S=πr2,代入数据进行解答即可。
【详解】3.14×32
=3.14×9
=28.26(cm2)
所得到立体图形是圆锥,底面积为28.26cm2。
4.3.14
【分析】如果将圆柱形木桩切削成一个最大的圆锥,则圆锥相当于圆柱的,圆锥的高相当于圆柱的高,圆锥的底面相当于圆柱的底面,根据圆锥的体积公式:V=πr2h,用3.14×(2÷2)2×3×即可求出圆锥的体积。
【详解】3.14×(2÷2)2×3×
=3.14×12×3×
=3.14×1×3×
=3.14(立方分米)
削成后的圆锥的体积是3.14立方分米。
5.6
【分析】根据圆锥的体积公式:V=Sh,那么h=V÷÷S,据出解答。
【详解】36÷÷18
=36×3÷18
=108÷18
=6(分米)
它的高是6分米。
6.4
【分析】根据等底等高圆锥的体积是圆柱体积的,已知圆锥和圆柱等底等体积,圆锥的高是12cm,那么圆柱的高是圆锥高的,由此解答。
【详解】12×=4(cm)
圆柱的高是4cm。
7.47.1
【分析】这堆沙的体积不变,根据圆锥的体积公式求出这堆沙的体积,再除以10,除以0.04,就是可铺的长,据此解答。
【详解】4cm=0.04m
×12.56×4.5÷10÷0.04
=×56.52÷10÷0.04
=18.84÷10÷0.04
=1.884÷0.04
=47.1(m)
能铺47.1m。
8. 113.04 339.12 339.12 113.04
【分析】根据圆柱的侧面积公式:S=2πrh,圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【详解】圆柱的侧面积:2×3.14×6×3
=6.28×6×3
=37.68×3
=113.04(dm2)
圆柱的表面积:113.04+3.14×62×2
=113.04+113.04×2
=113.04+226.08
=339.12(dm2)
圆柱的体积:3.14×62×3
=113.04×3
=339.12(dm3)
圆锥的体积:339.12×=113.04(dm3)
9.(1) 9 1 (2) 27 1
【分析】(1)根据三角形的面积=底×高÷2,计算出两个图形的面积,根据比的意义写出比,化简比即可;
(2)根据题意,图①旋转得到的圆锥的底面半径是30cm,高是40cm;图②旋转得到的圆锥的底面半径是(30÷3)cm,高是(40÷3)cm,根据公式:圆锥的体积=底面积×高×计算出结果,根据比的意义写出比,化简比即可。
【详解】(1)图①的面积:
30×40÷2
=1200÷2
=600(cm2)
图②的面积:
(30÷3)×(40÷3)÷2
=10××
=(cm2)
所以,S①∶S②=600∶=9∶1
(2)V①:
30×30×π×40×
=900××π×40
=300×40×π
=12000π(cm3)
V②:
(30÷3)×(30÷3)×π×(40÷3)×
=10×10×π××
=100π×
=π(cm3)
12000π∶π=27∶1
所以V①∶V②=27∶1
10.C
【分析】根据对圆柱和圆锥的认识,长方形旋转一周得到一个圆柱,直角三角形旋转一周得到一个圆锥。据此解题。
【详解】将直角三角形ABC,绕直角边AC旋转一周,便形成了圆锥。其中AC是圆锥的高;CB是圆锥底面的半径。
如图:
故答案为:C
11.C
【分析】根据面动成体判断出各选项中旋转得到立体图形即可得解。
【详解】A.以直角三角形的一条直角边为轴旋转,可以得到一个圆锥;
B.以长方形的一条边为轴旋转,可以得到一个圆柱;
C.以直角梯形的下底为轴旋转,可以得到一个圆柱和一个圆锥的组合图形。
故答案为:C
12.A
【分析】根据题意,把圆锥形木块沿底面直径切成完全相同的两块后,表面积比原来增加两个切面的面积,切面是一个底等于圆锥的底面直径,高等于圆锥的高的三角形;根据三角形的面积=底×高÷2,求出一个切面的面积,再乘2,即是增加的表面积。
【详解】6×9÷2×2
=54÷2×2
=54(cm2)
表面积比原来增加了54cm2。
故答案为:A
13.C
【分析】以直角三角形的一条直角边所在的直线为轴旋转一周,就可以得到一个圆锥,把圆锥沿着高平均切成两块之后,切面是一个以圆锥的高为高的等腰三角形,据此解答。
【详解】
如图所示,将一个圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
故答案为:C
14.B
【分析】根据V柱=Sh,V锥=Sh可知,当圆柱和圆锥等底等高时,圆柱的体积等于圆锥体积的3倍,即把圆锥的体积看作l份,圆柱的体积是3份,份数相差(3-1)份;用等底等高的圆柱和圆锥的体积之差除以份数差,求出一份数,即是圆锥的体积。
【详解】24÷(3-1)
=24÷2
=12(dm3)
圆锥的体积是12dm3。
故答案为:B
15.C
【分析】圆柱和圆锥的底面积相等,圆锥的高度为15cm,圆柱的高度为(19-15)cm,容器倒置后,圆锥里面的水在圆柱里面的高度为圆锥高度的,最后加上原来圆柱里面水的高度就是倒置后的水面高度,据此解答。
【详解】15×+(19-15)
=5+4
=9(cm)
水面的高度是9cm。
故答案为:C
16.B
【分析】已知圆锥的底面周长是18.84厘米,根据圆周长公式:C=2πr,用18.84÷3.14÷2即可求出圆锥的底面半径,再根据圆锥的体积公式:V=πr2h求出圆锥的体积。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×5×
=3.14×9×5×
=47.1(立方厘米)
圆锥的体积是47.1立方厘米。
故答案为:B
17.A
【分析】利用圆的周长公式、比的定义及性质、圆的性质分别判断后即可确定正确的选项。
【详解】①一个圆的周长总是它的直径的π倍,故①错误;
②甲数除以乙数(不等于0)等于甲数乘乙数的倒数,说法正确,故②正确;
③圆锥以及圆柱的体积还与底面积有关,说法错误,故③错误;
④比的前项和比的后项同时乘或除以一个相同的数(不为0),比值不变,原说法错误,故④错误;
正确的有1个。
故答案为:A
18.A
【分析】等底等高的圆柱的体积是圆锥的体积的3倍,所以用圆柱的体积除以3即可求出圆锥的体积,由此即可解答。
【详解】141.3÷3=47.1(立方米)
一个圆柱的体积是141.3立方米,与它等底等高的圆锥的体积是47.1立方米。
故答案为:A
19.√
【分析】根据:圆锥的体积=底面积×高×,底面积=π×r2,若底面直径扩大到原来的a倍,高不变,那么底面半径也扩大到原来的a倍,则圆锥的体积会扩大到原来的a2倍,据此判断即可。
【详解】根据分析,2×2=4
圆锥的高不变,底面直径扩大到原来的2倍,它的体积就扩大到原来的4倍,说法正确;
故答案为:√
20.×
【分析】根据圆锥的体积计算公式“V=”得出:圆锥的体积不但与圆锥的底面半径有关,还跟圆锥的高有关;只有在高相同的情况下,圆锥的底面半径越大,它的体积就越大;不能只凭一种情况,就下结论。
【详解】根据分析得,当高一定的情况下,底面半径越大的圆锥,底面积就越大,体积也就越大。所以原题的说法是错误的。
故答案为:×
21.×
【分析】圆柱的体积等于圆锥体积的3倍,根据圆柱的体积公式:V柱=πr2h,圆锥的体积公式:V锥=πr2h,圆柱的体积和圆锥的体积由底面半径和高确定,所以两个条件都未知,无法判断它们是否等底等高。
【详解】根据题意可知,如果圆柱的体积等于圆锥体积的3倍,那么它们不一定等底等高,原题干说法错误。
故答案为:×
22.×
【分析】因为等底等高的圆锥的体积是圆柱体积的,把圆柱的体积看作单位“1”,根据求一个数比另一个少几分之几,用除法解答。
【详解】把圆柱的体积看作单位“1”,
(1-)÷1
=÷1
=
即圆锥的体积比圆柱小。
故答案为:×
23.×
【分析】以直角三角形的一条直角边为轴旋转一周可得到一个圆锥,据此判断。
【详解】等腰三角形也是直角三角形时,以直角三角形的一条直角边为轴旋转一周可形成一个圆锥。
原题说法错误。
故答案为:×
24.×
【分析】根据旋转的特点,以直角三角形任意一条直角边旋转一周,都可以得到一个圆锥体。据此解答。
【详解】任何一个直角三角形以任意一条直角边为轴旋转一周,都可以得到一个圆锥,而不是任意一边,当它以斜边旋转一周时得到的就不是圆锥体了,本题结论是错误的。
故答案为:×
25.37.68立方厘米
【分析】根据题意,图形围绕虚线旋转一周后形成的立体图形是底面半径为3厘米,高为4厘米的圆锥,根据公式:圆锥的体积=底面积×高×,底面积=πr2,将数据代入计算即可。
【详解】3.14×32×4×
=28.25×4×
=113.04×
=37.68(立方厘米)
26.(1)47.1立方厘米;(2)37.68立方分米
【分析】圆锥的体积= ×底面积×高= πr h,半径=直径÷2,代入公式计算即可。
【详解】(1)6÷2=3(厘米)
×3.14×3 ×5
=9.42×5
=47.1(立方厘米)
(2)3.14×2 ×9×
=12.56×9×
=37.68(立方分米)
27.【分析】根据测量圆锥高的方法进行解答即可。
【详解】测量圆锥高的方法:
①先把圆锥的底面放平
②用一块平板水平地放在圆锥的顶点上面
③竖直地量出平板和底面之间的距离
28.19.625平方米
【分析】求圆锥的占地面积,就是求直径是5米的圆的面积,根据圆的面积=πr2,代入数据,即可解答。
【详解】3.14×(5÷2)2
=3.14×2.52
=19.625(平方米)
这种圆锥形帐篷占地面积是19.625平方米。
29.84.78立方厘米
【分析】根据圆柱的底面半径r=C÷π÷2,先求出圆柱形容器的底面半径;把圆锥体浸没在装有水的圆柱形容器里,水面升了3厘米,那么水面升高部分的体积等于这个圆锥的体积;根据圆柱的体积公式V=πr2h,代入数据计算即可。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×3
=3.14×9×3
=3.14×27
=84.78(立方厘米)
答:这个圆锥体的体积是84.78立方厘米。
30.4厘米
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥的体积,圆柱的体积是圆锥体积的4倍,把数据代入公式求出圆柱的体积,再根据圆柱的体积公式:V=πr2h,那么h=V÷πr2,把数据代入公式解答。
【详解】×3.14×(4÷2)2×3×4÷[3.14×(4÷2)2]
=×3.14×(4÷2)2×3×4÷[3.14×4]
=×3.14×4×3×4÷[3.14×4]
=×12.56×3×4÷12.56
=×37.68×4÷12.56
=12.56×4÷12.56
=50.24÷12.56
=4(厘米)
答:圆柱的高是4厘米时能使陀螺转得又快又稳。
31.45吨
【分析】此题需要先利用圆的周长公式求出这堆煤的底面半径,再利用圆锥的体积V=Sh,求出这堆煤的体积,进而用这堆煤的体积乘每立方米的煤的重量,就是这堆煤的总重量。
【详解】底面半径:25.12÷(2×3.14)
=25.12÷6.28
=4(米)
这堆煤的体积:
×3.14×42×1.8
=×3.14×16×1.8
=×50.24×1.8
=×90.432
=30.144(立方米)
这堆煤的重量:30.144×1.5≈45(吨)
答:这堆煤共重45吨。
32.10厘米
【分析】先求出正方体的体积,正方体的体积=棱长×棱长×棱长,因为将正方体铁块熔铸成圆锥形铁块,所以体积相等;圆锥的体积=×底面积×高,则圆锥的高=圆锥的体积÷底面积÷,圆锥的底面是一个圆,圆的面积=πr2,代入公式计算即可。
【详解】10×10×10=1000(立方厘米)
3×(20÷2)2
=3×100
=300(平方厘米)
1000÷300÷
=1000÷300×3
=10(厘米)
答:圆锥形铁块的高约是10厘米。
33.(1)15厘米
(2)160π立方厘米
(3)10个;4.4厘米
【分析】(1)先根据圆的底面周长公式C=2πr,求出圆柱的底面周长;再根据圆柱的侧面积公式S侧=Ch可知,圆柱的高h=S侧÷C,代入数据计算即可求出圆柱形容器的高。
(2)根据“实心铁圆柱的高为圆柱形容器高的”,把圆柱形容器的高看作单位“1”,单位“1”已知,用乘法求出实心铁圆柱的高;
根据“实心铁圆柱的底面半径比圆柱形容器的底面半径小”,把圆柱形容器的底面半径看作单位“1”,单位“1”已知,用乘法求出实心铁圆柱的底面半径;
然后根据圆柱的体积公式V=πr2h,求出这个实心铁圆柱的体积。
(3)已知实心冰圆锥的底面半径和高,根据圆锥的体积公式V=πr2h,求出一个实心冰圆锥的体积;
已知水变成冰体积会增加,即冰的体积比水的体积增加,把水的体积看作单位“1”,冰的体积是水体积的(1+),单位“1”未知,用除法计算,求出一个实心冰圆锥化成水后的体积;
现将实心铁圆柱体放入圆柱形容器,水要浸没实心铁圆柱体,水的高度至少等于实心铁圆柱体的高10厘米,根据圆柱的体积公式V=πr2h,求出水和实心铁圆柱体的总体积;再减去实心铁圆柱体的体积,就是至少需要水的体积;用水的体积除以一个实心冰圆锥的体积,即可求出至少需要实心冰圆锥的个数,得数用进一法取整数。
用实心铁圆柱体的体积加上10个实心冰圆锥的体积,除以圆柱形容器的底面积,求出此时水面的高度,再用圆柱形容器的高减去水面的高度,即可求出此时水面与容器口的距离。
【详解】(1)圆柱的底面周长:2×π×10=20π(厘米)
圆柱的高:300π÷20π=15(厘米)
答:该圆柱形容器的高为15厘米。
(2)实心铁圆柱的高:15×=10(厘米)
实心铁圆柱的底面半径:
10×(1-)
=10×
=4(厘米)
实心铁圆柱体的体积:
π×42×10
=π×16×10
=160π(立方厘米)
答:该实心铁圆柱体的体积是160π立方厘米。
(3)一个实心冰圆锥的体积:
×π×52×12
=×π×25×12
=100π(立方厘米)
一个实心冰圆锥化成水的体积:
100π÷(1+)
=100π÷
=100π×
=90π(立方厘米)
与实心铁圆柱体高相等的水的体积:
π×102×10
=π×100×10
=1000π(立方厘米)
恰好浸没实心铁圆柱体需要水:
1000π-160π=840π(立方厘米)
需要实心冰圆锥:
840π÷90π≈10(个)
水面的高度:
(160π+90π×10)÷(π×102)
=1060π÷100π
=10.6(厘米)
水面与容器口的距离:
15-10.6=4.4(厘米)
答:此时水面与容器口的距离h为4.4厘米。
答案第1页,共2页
答案第1页,共2页
