有理数的乘法[上学期]

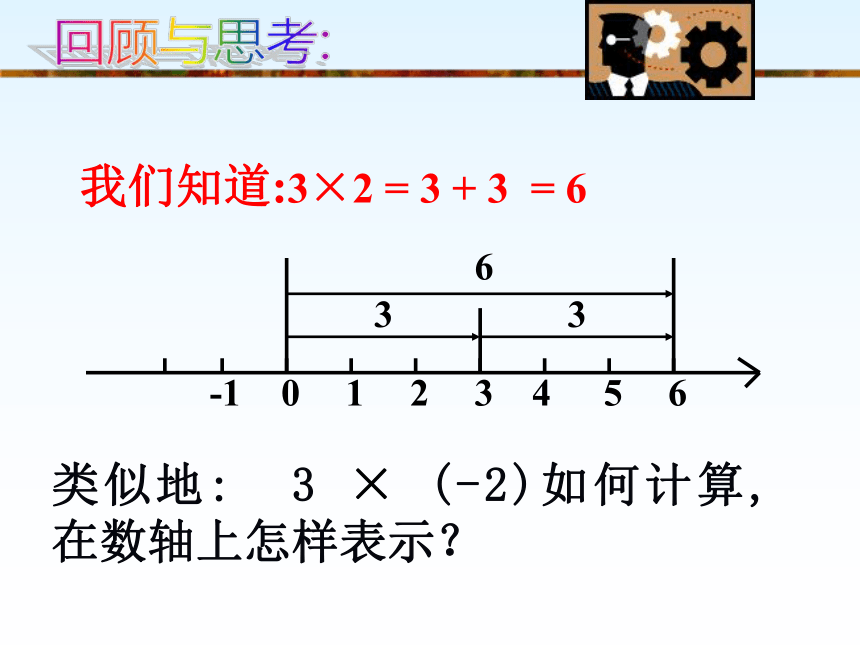
课件23张PPT。有理数的乘法（１）２００６.９.２２我们知道:3×2 = 3 + 3 = 60123456-1633类似地: 3 × (-2)如何计算, 在数轴上怎样表示？回顾与思考:水库水位的变化
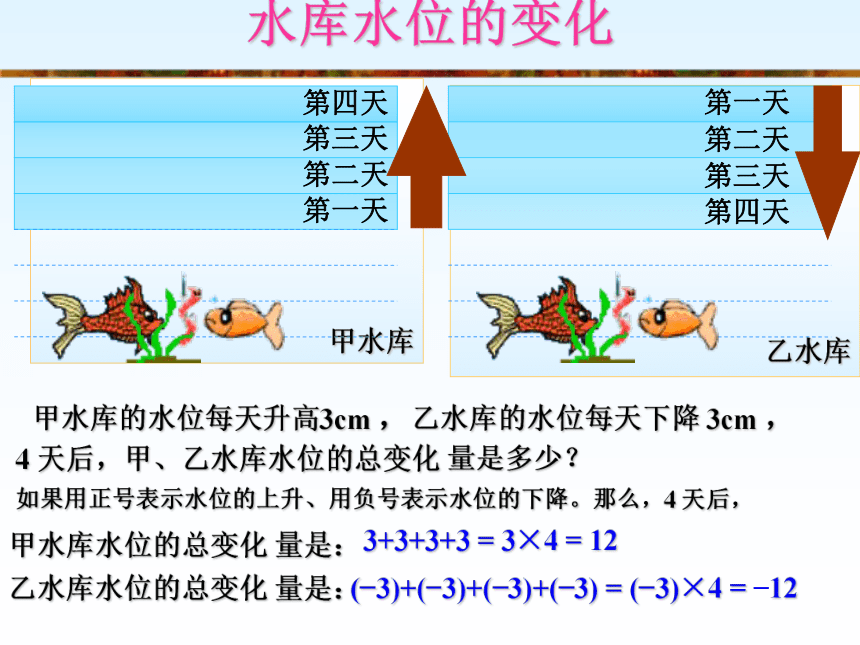
甲水库第一天甲水库的水位每天升高3cm ，第二天第三天第四天4 天后，甲水库水位的总变化 量是多少？ 如果用正号表示水位的上升、用负号表示水位的下降。那么，4 天后，甲水库水位的总变化 量是：
3+3+3+3 = 3×4 = 12水库水位的变化
甲水库第一天
乙水库甲水库的水位每天升高3cm ，第二天第三天第四天乙水库的水位每天下降 3cm ， 第一天 第二天 第三天 第四天4 天后，甲、乙水库水位的总变化 量是多少？如果用正号表示水位的上升、用负号表示水位的下降。那么，4 天后，甲水库水位的总变化 量是：
3+3+3+3 = 3×4 = 12(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12
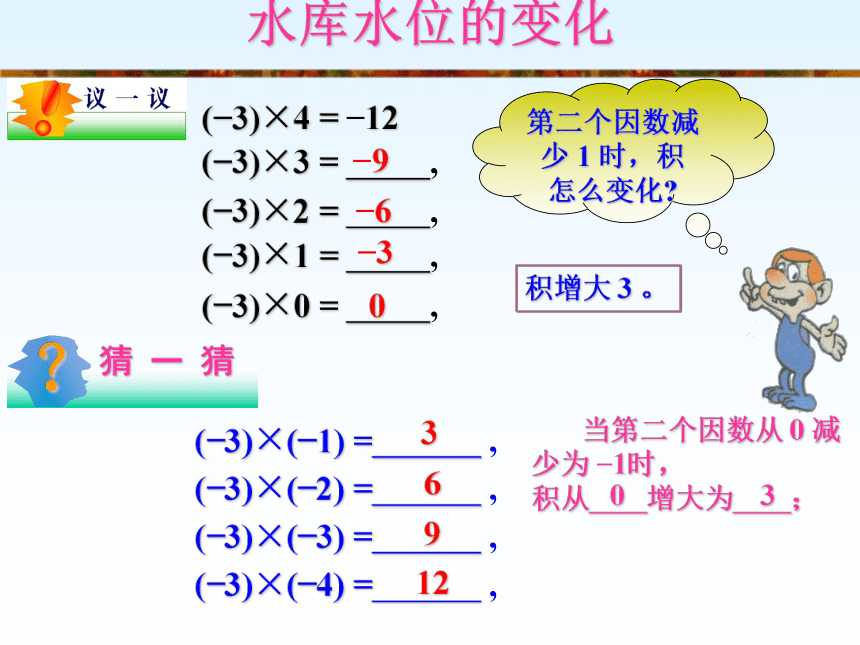
乙水库水位的总变化 量是：水库水位的变化(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时，积 怎么变化?36912 当第二个因数从 0 减少为 ?1时，
积从 增大为 ；积增大 3 。03探 究(?3)×4 = ?12 (?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,36912由上述所列各式 , 你能看出两有理数相乘,因数与它们的积之间的规律吗? 负数乘正数积为负，绝对值相乘； 负数乘 0 得0 ； 负数乘负数积为正，绝对值相乘；试一试，你也很棒哦！说出下列各个算式的结果：３ × 7 , (-3) ×(-7) , (-3) × 7 , 7 ×(-3) ,0 ×(-3)由此你认为两个有理数相乘有哪些规律？+２１+２１－２１－２１０有理数的乘法法则两数相乘，同号得 ，异号得 ，并把绝对值相乘；任何数与零相乘得 。正负零口答：
(1)6×(-9)； (2)(-6)×(-9)； (3)(-6)×9； (4)(-6)×1； (5)(-6)×(-1)； (6)6×(-1)； (7)(-6)×0； (8)0×(-6)； (9)(-6)×0×25
(10)(-0.5)×(-8)；
看谁做得又快又准.例 题 解 析例1 计算：
(1) (?4)×5 ； (2) (?4)×(?7) ；
(3) (4)解：(1) (?4)×5 (2) (?4)×(?7)
= ?(4×5) =+(4×7)
=?20 ; =28;(3) (4)=1 ;=1 ;求解中的第一步是 ；确定积的符号 第二步
是 ；绝对值相乘倒 数 的 定 义 由例 1 的 (3) 、(4)的求解:? 解题后的反思 ? (3) (4)=1 ;=1 ;可知 我们把乘积为 1 的两个有理数称作互为倒数.我来说一说：请说出下列各数的倒数：( 1 )（ 3 ）－２（ 2 ）（４）（５）－２.５( 7 )( 8 )( 6 ) 1( 9 ) 0－1例 题 解 析例2 计算：
(1) (?4)×5×(?0.25)；
解： (?4)×5 ×(?0.25)
= [?(4×5)]×(?0.25) =+(20×0.25)=5.=(?20)×(?0.25) 三个有理数相乘时，先把前两个相乘，再把所得结果与另一个数相乘．例 题 解 析例2 计算：
(1) (?4)×5×(?0.25)； (2)
解：(1) (?4)×5 ×(?0.25)
＝ [?(4×5)]×(?0.25) ＝＋(20×0.25)＝5.＝(?20)×(?0.25)(2) ＝?1 .+?例2 计算：
(1) (?4)×5×(?0.25)； (2)
解：(1) (?4)×5 ×(?0.25)
(2) +? 有一因数为 0 时，积是多少？ 几个有理数相乘，因数都不为 0 时，
积的符号怎样确定？乘积 的符号 的确定乘积 的符号 的确定 几个有理数相乘，因数都不为 0 时
积的符号由 确定：负因数的个数负因数个数为奇数个时, 积为负，负因数个数为偶数个时, 积为正。 有一个因数为 0 时，积是0 。观察下列各式，它们的积是正的还是负的？
（1）（-1） ×2 ×3 ×4
（2） （-1） ×（-2 ）×3 ×4
（3） （-1） ×（-2 ）×（-3 ）×4
（4） （-1） ×（-2 ）×（-3 ）×（-4）
（5） （-1） ×（-2 ）×（-3 ）×（-4）×0
可要看清楚哦温馨提示:计算下列各式：①
②
③
④
⑤
认真算算,这些重点是不是真的都掌握了?和以前学过的乘法相比有什么区别和联系?填空(用“＞”或“＜”号连接)：
(1)如果a＜0，b＜0，那么ab 0；
(2)如果a＜0，b ＞ 0，那么ab 0；
(3)如果 a ＞ 0，b ＞ 0，那么ab 0；
(4)如果ab＜0，那么a 0,b 0;
(5) 如果 ab ＞ 0, 那么a 0,b 0.
＞＜＞做做看,你的能耐是不是真的有长进了?把－６表示成两个整数的积，有多少种可能性？你能把他们全部写出来吗？挑战自己，其实我很棒的！！1、本节课你学到了什么？小结与思考2、本节课你印象最深的是什么？3、本节课后你还有什么疑问？重点知识回顾1、两数相乘，同号得 ，异号得 ，
绝对值相乘；0 乘 任何数得 。正负0 2、几个有理数相乘，因数都不为 0 时，
积的符号由 确定：负因数的个数奇数个为负，偶数个为正。 有一因数为 0 时，积是0 。0没有倒数,倒数等于本身的数是+1,-1.3、恳请各位老师多提宝贵建议
谢 谢