北京市密云县2014年中考数学模拟试卷(二模)(附答案及评分标准)
文档属性
| 名称 | 北京市密云县2014年中考数学模拟试卷(二模)(附答案及评分标准) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-10 10:59:04 | ||
图片预览



文档简介
密云县2014年初三质量检测(二)
数学试卷
考生须知 1. 本试卷共6页,共五道大题,25道小题,满分120分。考试时间120分钟。2. 在试卷和答题卡上准确填写学校名称、姓名、班级和考号。3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效。4. 在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。5. 考试结束,将本试卷、答题卡和草稿纸一并交回。
选择题(本题共32分,每小题4分)
下面各题均有四个选项,其中只有一个是符合题意的.
1. 的相反数是
A. B. C. D.9
2.十八大开幕当天,网站关于此信息的总浏览量达550000000次.将550000000用科学记数法表示为
A. B. C. D.
3.一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其它区别,现
从这个盒子中随机摸出一个球,摸到红球的概率为
A. B. C. D.
4.如图,直线、相交于点,, ,
则∠AOC等于
A.54° B.46°
C.36° D.26°
5.如图是某几何体的三视图,则这个几何体是
A. 圆柱 B. 正方体
C. 球 D. 圆锥
6. 2013年5月某日我国部分城市的最高气温统计如下表所示:
城市 武汉 成都 北京 上海 海南 南京 拉萨 深圳
气温(℃) 27 27 24 25 28 28 23 26
请问这组数据的平均数是
A. 25 B.26 C.27 D.28
7.一个多边形的外角和是内角和的一半,则这个多边形的边数为
A. 8 B.7 C. 6 D. 5
8.如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C
的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本题共16分,每小题4分)
9.分解因式:
10.若 是关于x、y的二元一次方程 的解,则a的值为
11.如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球
从N点击到了对方场内的点B,已知网高OA=1.52米,OB=4米,
OM=5米,则林丹起跳后击球点N离地面的距离MN= 米.
12.如图,设四边形是边长为1的正方形,以正方形的对角
线为边作第二个正方形,再以第二个正方形的对角线
为边作第三个正方形,如此下去.
(1)记正方形的边长为,按上述方法所作的
正方形的边长依次为,,,,,求出= ;
(2) 根据以上规律写出第个正方形的边长的表达式 .(n>=1)(是自然数)
三、解答题(本题共30分,每小题5分)
13. 计算:
14. 已知:如图,
求证:
15.(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;
16.先化简,再计算:
已知: 求代数式 的值.
17.如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
18.列方程或方程组解应用题:
)李明到离家2.1千米的学校参加初三联欢会 ( http: / / www.21cnjy.com ),到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.求李明步行的速度(单位:米/分)是多少?
四、解答题(本题共20分,每小题5分)
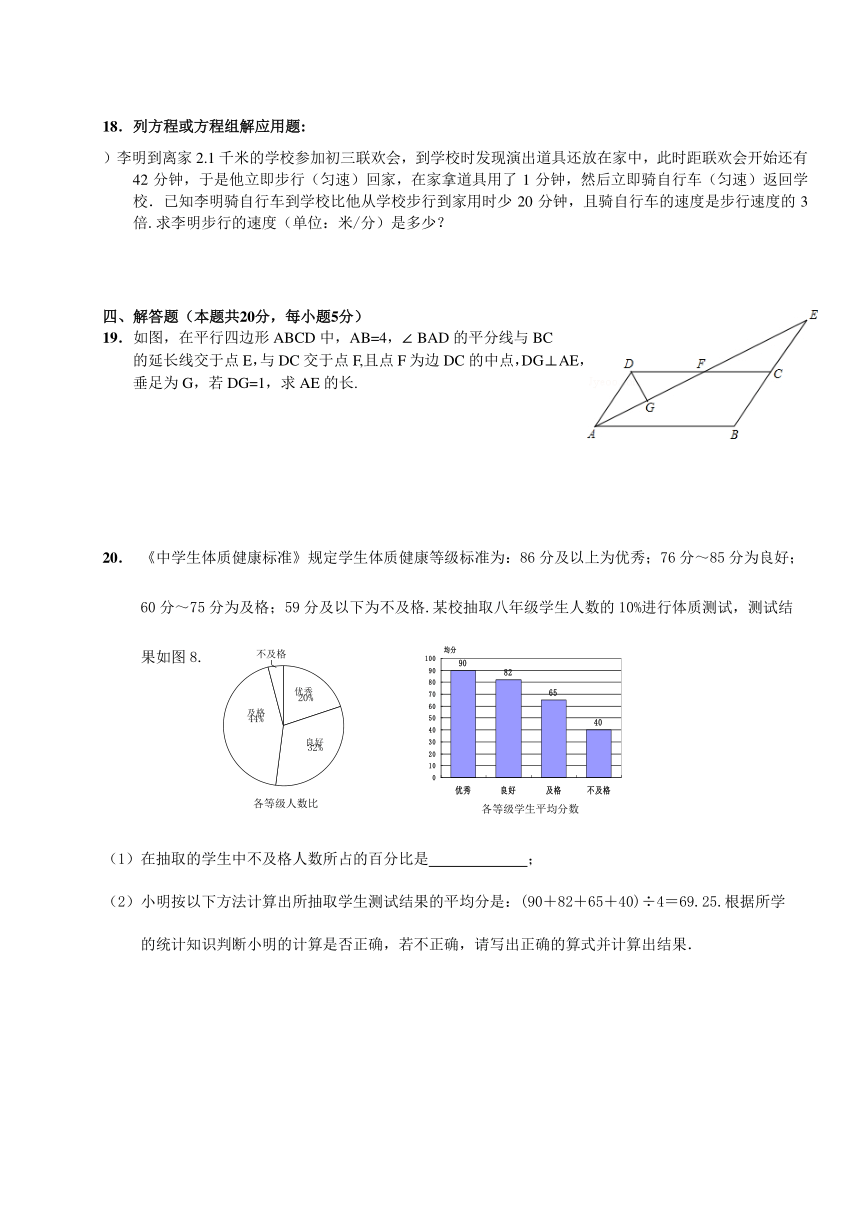
19.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC
的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,
垂足为G,若DG=1,求AE的长.
20. 《中学生体质健康标准》规定学生体质健康等级标准为:86分及以上为优秀;76分~85分为良好;
60分~75分为及格;59分及以下为不及格.某校抽取八年级学生人数的10%进行体质测试,测试结
果如图8.
(1)在抽取的学生中不及格人数所占的百分比是 ;
(2)小明按以下方法计算出所抽取学生测试结果的平均分是:(90+82+65+40)÷4=69.25.根据所学
的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式并计算出结果.
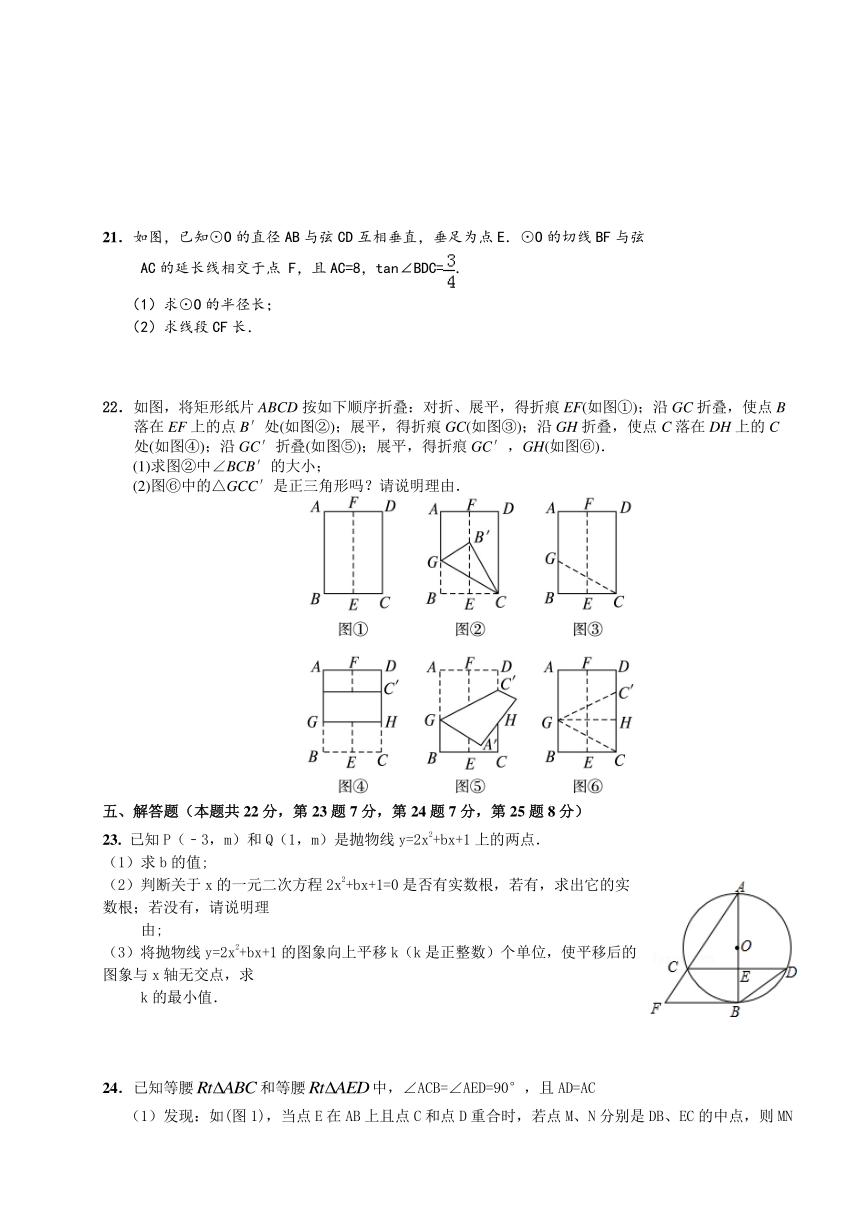
21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦
AC的延长线相交于点 F,且AC=8,tan∠BDC=.
(1)求⊙O的半径长;
(2)求线段CF长.
22.如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B
落在EF上的点B′处(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的C
处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′的大小;
(2)图⑥中的△GCC′是正三角形吗?请说明理由.
( http: / / www.21cnjy.com )
五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)
23. 已知P(﹣3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)判断关于x的一元二次方程2x2+bx+1=0是否有实数根,若有,求出它的实数根;若没有,请说明理
由;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位,使平移后的图象与x轴无交点,求
k的最小值.
24.已知等腰和等腰中,∠ACB=∠AED=90°,且AD=AC
(1)发现:如(图1),当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN
与EC的位置关系是 ,MN与EC的数量关系是
(2)探究:若把(1)小题中的△AED绕点A旋转一定角度,如(图2)所示,连接BD和EC,并连接DB、
EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,以顺时针旋转45°
得到的图形(图3)为例给予证明数量关系成立,若不成立,请说明理由;请以逆时针旋转45°
得到的图形(图4)为例给予证明位置关系成立,
25.按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,
这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含
20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(一)新数据都在60~100(含60和100)之间;
(二)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对
应的新数据也较大.
若y与x的关系是y=x+p(100-x),请说明:当p=时,这种变换满足上述两个要求;
若按关系式y=a(x-h) ( http: / / www.21cnjy.com )2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式.(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
三120Wcm1.52、T/2 D、 ( http: / / www.21cnjy.com ) 密云县2014年初中毕业考试(二)
数学试卷答案及评分标准
一、选择题(本题共32分,每小题4分)
1.D 2.A 3.B 4.C 5.D 6.B 7.C
8.B解:∵等边三角形ABC的边长为3,N为AC的三等分点,
∴AN=1.
∴当点M位于点A处时,x=0,y=1.
动点M从A点出发到AM=1的过程中,y随x的增大而减小,故排除D;
当动点M到达C点时,x=6,y=3﹣1=2,即此时y的值与点M在点A处时的值不
相等.故排除A、C,故选B.
二、填空题(本题共16分,每小题4分)
9. 10.5 11. 3.42
12. ,
(是自然数)
三、解答题(本题共30分,每小题5分)
13.
14.证明:∥,
∴ ………………………1分
在△和△中,
∴△≌△.………………………3分
∴ ………………………4分
15. 10x-10+8<6x-6+7…………………1分
10x-6x<10-8-6+7………………2分
4x<3………………4分
………………5分
HYPERLINK "http://www.21cnjy.com"
17. (1) ∵OA=OB=OD=1,
∴点A、B、D的坐标分别为A(﹣1,0),B(0,1),D(1,0);………………….3分
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴,解得,
∴一次函数的解析式为y=x+1.……………………………………………………………4分
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2),
又∵点C在反比例函数 的图象上,
∴m=2;
∴反比例函数的解析式为y=.………………………………………………………5分
18. 设步行速度为米/分,则自行车的速度为米/分.
根据题意得:
得
经检验是原方程的解,
答:李明步行的速度是70米/分. 5分
四、解答题(本题共20分,每小题5分)
19.∵AE为∠ADB的平分线,
∴∠DAE=∠BAE,………………………………………………….1分
∵DC∥AB,
∴∠BAE=∠DFA,………………………………………………….2分
∴∠DAE=∠DFA,
∴AD=FD,
又F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB=2,
在Rt△ADG中,根据勾股定理得:AG=,……….3分
则AF=2AG=2,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4.……………………………………………………….5分
20. (1)4% …………………………………2分
(2)不正确
正确的算法:90×20%+82×32%+65×44%+40×4%=74.44………………5分
21. (1)作OH⊥AC于H,则AH=AC=4,…………………………1分
在Rt△AOH中,AH=4,tanA=tan∠BDC=,
∴OH=3,
∴半径OA==5;………………………2分
(2)∵AB⊥CD,
∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA=,
设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=,
则CE=DE=,AE=,
∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴=,即=,
解得:AF=,
则CF=AF﹣AC=.…………………………………5分
22. (1)连接BB′,由折叠知,EF是线段BC的对称轴,
∴BB′=B′C.
又∵BC=B′C,
∴△B′BC是等边三角形,
∴∠BCB′=60°. ……………2分
(2)由折叠知,GH是线段CC′的对称轴,
∴G′C=GC.
根据题意,GC平分∠BCB′,
∴∠GCB=∠GCB′=∠BCB′=30°.
∴∠GCC′=∠BCD-∠BCG=60°.
∴△GCC′是等边三角形.……………5分
、解答题(本题共22分,第23题7分,第24题7分,第25题8分)
23. (1)∵点P、Q在抛物线上且纵坐标相同,
∴P、Q关于抛物线对称轴对称并且到对称轴距离相等.
∴抛物线对称轴,
∴b=4.
(2)由(1)可知,关于x的一元二次方程为2x2+4x+1=0.
∵△=b2﹣4ac=16﹣8=8>0,
∴方程有实根,
∴x===﹣1±;
(3)由题意将抛物线y=2x2+bx+1的图象向上平移k(k 是正整数)个单位,使平移后的图象与x
轴无交点,
∴设为y=2x2+4x+1+k,∴方程2x2+4x+1+k=0没根,
∴△<0,
∴16﹣8(1+k)<0,
∴k>1,
∵k是正整数,
∴k的最小值为2.
24.(1).------------1分
(2)连接EF并延长交BC于F,
∵∠AED=∠ACB=90°
∴DE∥BC
∴∠DEM=∠AFM,∠EDM=∠MBF
又BM=MD
∴△EDM≌△FBM
∴BF=DE=AE,EM=FM
∴--------------4分
延长ED到F,连接AF、MF,则AF为矩形ACFE对角线,所以比经过EC的中点N且AN=NF=EN=NC.
在Rt△BDF中,M是BD的中点,∠B=45°
∴FD=FB
∴FM⊥AB,
∴MN=NA=NF=NC
∴点A、C、F、M都在以N为圆心的圆上
∴∠MNC=2∠DAC
由四边形MACF中,∠MFC=135°
∠FMA=∠ACB=90°
∴∠DAC=45°
∴∠MNC=90°即MN⊥FC-------------------7分
25. (1)又当x=20时,.而原数据都在20~100之间,所以新数据都在60~100
之间, 即满足条件(一),……1分
当 时, ,即y= .∴y随着x的增大而增大,即
时,满足条件(二)
综上可知,当 时,这种变换满足要求;……2分
(2)本题是开放性问题,答案不唯一。若所给出的关系式满足:(a)h≤20;(b)若x=20,100时,
y的对应值m,n能落在60~100之间,则这样的关系式都符合要求。
如取h=20, ,……8分
∵a>0,∴当20≤x≤100时,y随着x的增大…10分
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×802+k=100 ②
由①②解得 , ∴ ……8分
A
O
D
B
E
C
J
I
E
C
B
A
H
G
F
D
优秀
良好
及格
各等级人数比
各等级学生平均分数
(图4)
(图3)
(图2)
(图1)
数学试卷
考生须知 1. 本试卷共6页,共五道大题,25道小题,满分120分。考试时间120分钟。2. 在试卷和答题卡上准确填写学校名称、姓名、班级和考号。3. 试题答案一律填涂或书写在答题卡上,在试卷上作答无效。4. 在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。5. 考试结束,将本试卷、答题卡和草稿纸一并交回。
选择题(本题共32分,每小题4分)
下面各题均有四个选项,其中只有一个是符合题意的.
1. 的相反数是
A. B. C. D.9
2.十八大开幕当天,网站关于此信息的总浏览量达550000000次.将550000000用科学记数法表示为
A. B. C. D.
3.一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其它区别,现
从这个盒子中随机摸出一个球,摸到红球的概率为
A. B. C. D.
4.如图,直线、相交于点,, ,
则∠AOC等于
A.54° B.46°
C.36° D.26°
5.如图是某几何体的三视图,则这个几何体是
A. 圆柱 B. 正方体
C. 球 D. 圆锥
6. 2013年5月某日我国部分城市的最高气温统计如下表所示:
城市 武汉 成都 北京 上海 海南 南京 拉萨 深圳
气温(℃) 27 27 24 25 28 28 23 26
请问这组数据的平均数是
A. 25 B.26 C.27 D.28
7.一个多边形的外角和是内角和的一半,则这个多边形的边数为
A. 8 B.7 C. 6 D. 5
8.如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C
的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )
( http: / / www.21cnjy.com )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本题共16分,每小题4分)
9.分解因式:
10.若 是关于x、y的二元一次方程 的解,则a的值为
11.如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球
从N点击到了对方场内的点B,已知网高OA=1.52米,OB=4米,
OM=5米,则林丹起跳后击球点N离地面的距离MN= 米.
12.如图,设四边形是边长为1的正方形,以正方形的对角
线为边作第二个正方形,再以第二个正方形的对角线
为边作第三个正方形,如此下去.
(1)记正方形的边长为,按上述方法所作的
正方形的边长依次为,,,,,求出= ;
(2) 根据以上规律写出第个正方形的边长的表达式 .(n>=1)(是自然数)
三、解答题(本题共30分,每小题5分)
13. 计算:
14. 已知:如图,
求证:
15.(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;
16.先化简,再计算:
已知: 求代数式 的值.
17.如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
18.列方程或方程组解应用题:
)李明到离家2.1千米的学校参加初三联欢会 ( http: / / www.21cnjy.com ),到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.求李明步行的速度(单位:米/分)是多少?
四、解答题(本题共20分,每小题5分)
19.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC
的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,
垂足为G,若DG=1,求AE的长.
20. 《中学生体质健康标准》规定学生体质健康等级标准为:86分及以上为优秀;76分~85分为良好;
60分~75分为及格;59分及以下为不及格.某校抽取八年级学生人数的10%进行体质测试,测试结
果如图8.
(1)在抽取的学生中不及格人数所占的百分比是 ;
(2)小明按以下方法计算出所抽取学生测试结果的平均分是:(90+82+65+40)÷4=69.25.根据所学
的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式并计算出结果.
21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦
AC的延长线相交于点 F,且AC=8,tan∠BDC=.
(1)求⊙O的半径长;
(2)求线段CF长.
22.如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B
落在EF上的点B′处(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的C
处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′的大小;
(2)图⑥中的△GCC′是正三角形吗?请说明理由.
( http: / / www.21cnjy.com )
五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)
23. 已知P(﹣3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.
(1)求b的值;
(2)判断关于x的一元二次方程2x2+bx+1=0是否有实数根,若有,求出它的实数根;若没有,请说明理
由;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位,使平移后的图象与x轴无交点,求
k的最小值.
24.已知等腰和等腰中,∠ACB=∠AED=90°,且AD=AC
(1)发现:如(图1),当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN
与EC的位置关系是 ,MN与EC的数量关系是
(2)探究:若把(1)小题中的△AED绕点A旋转一定角度,如(图2)所示,连接BD和EC,并连接DB、
EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,以顺时针旋转45°
得到的图形(图3)为例给予证明数量关系成立,若不成立,请说明理由;请以逆时针旋转45°
得到的图形(图4)为例给予证明位置关系成立,
25.按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,
这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含
20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(一)新数据都在60~100(含60和100)之间;
(二)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对
应的新数据也较大.
若y与x的关系是y=x+p(100-x),请说明:当p=时,这种变换满足上述两个要求;
若按关系式y=a(x-h) ( http: / / www.21cnjy.com )2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式.(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
三120Wcm1.52、T/2 D、 ( http: / / www.21cnjy.com ) 密云县2014年初中毕业考试(二)
数学试卷答案及评分标准
一、选择题(本题共32分,每小题4分)
1.D 2.A 3.B 4.C 5.D 6.B 7.C
8.B解:∵等边三角形ABC的边长为3,N为AC的三等分点,
∴AN=1.
∴当点M位于点A处时,x=0,y=1.
动点M从A点出发到AM=1的过程中,y随x的增大而减小,故排除D;
当动点M到达C点时,x=6,y=3﹣1=2,即此时y的值与点M在点A处时的值不
相等.故排除A、C,故选B.
二、填空题(本题共16分,每小题4分)
9. 10.5 11. 3.42
12. ,
(是自然数)
三、解答题(本题共30分,每小题5分)
13.
14.证明:∥,
∴ ………………………1分
在△和△中,
∴△≌△.………………………3分
∴ ………………………4分
15. 10x-10+8<6x-6+7…………………1分
10x-6x<10-8-6+7………………2分
4x<3………………4分
………………5分
HYPERLINK "http://www.21cnjy.com"
17. (1) ∵OA=OB=OD=1,
∴点A、B、D的坐标分别为A(﹣1,0),B(0,1),D(1,0);………………….3分
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴,解得,
∴一次函数的解析式为y=x+1.……………………………………………………………4分
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2),
又∵点C在反比例函数 的图象上,
∴m=2;
∴反比例函数的解析式为y=.………………………………………………………5分
18. 设步行速度为米/分,则自行车的速度为米/分.
根据题意得:
得
经检验是原方程的解,
答:李明步行的速度是70米/分. 5分
四、解答题(本题共20分,每小题5分)
19.∵AE为∠ADB的平分线,
∴∠DAE=∠BAE,………………………………………………….1分
∵DC∥AB,
∴∠BAE=∠DFA,………………………………………………….2分
∴∠DAE=∠DFA,
∴AD=FD,
又F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB=2,
在Rt△ADG中,根据勾股定理得:AG=,……….3分
则AF=2AG=2,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4.……………………………………………………….5分
20. (1)4% …………………………………2分
(2)不正确
正确的算法:90×20%+82×32%+65×44%+40×4%=74.44………………5分
21. (1)作OH⊥AC于H,则AH=AC=4,…………………………1分
在Rt△AOH中,AH=4,tanA=tan∠BDC=,
∴OH=3,
∴半径OA==5;………………………2分
(2)∵AB⊥CD,
∴E为CD的中点,即CE=DE,
在Rt△AEC中,AC=8,tanA=,
设CE=3k,则AE=4k,
根据勾股定理得:AC2=CE2+AE2,即9k2+16k2=64,
解得:k=,
则CE=DE=,AE=,
∵BF为圆O的切线,
∴FB⊥AB,
又∵AE⊥CD,
∴CE∥FB,
∴=,即=,
解得:AF=,
则CF=AF﹣AC=.…………………………………5分
22. (1)连接BB′,由折叠知,EF是线段BC的对称轴,
∴BB′=B′C.
又∵BC=B′C,
∴△B′BC是等边三角形,
∴∠BCB′=60°. ……………2分
(2)由折叠知,GH是线段CC′的对称轴,
∴G′C=GC.
根据题意,GC平分∠BCB′,
∴∠GCB=∠GCB′=∠BCB′=30°.
∴∠GCC′=∠BCD-∠BCG=60°.
∴△GCC′是等边三角形.……………5分
、解答题(本题共22分,第23题7分,第24题7分,第25题8分)
23. (1)∵点P、Q在抛物线上且纵坐标相同,
∴P、Q关于抛物线对称轴对称并且到对称轴距离相等.
∴抛物线对称轴,
∴b=4.
(2)由(1)可知,关于x的一元二次方程为2x2+4x+1=0.
∵△=b2﹣4ac=16﹣8=8>0,
∴方程有实根,
∴x===﹣1±;
(3)由题意将抛物线y=2x2+bx+1的图象向上平移k(k 是正整数)个单位,使平移后的图象与x
轴无交点,
∴设为y=2x2+4x+1+k,∴方程2x2+4x+1+k=0没根,
∴△<0,
∴16﹣8(1+k)<0,
∴k>1,
∵k是正整数,
∴k的最小值为2.
24.(1).------------1分
(2)连接EF并延长交BC于F,
∵∠AED=∠ACB=90°
∴DE∥BC
∴∠DEM=∠AFM,∠EDM=∠MBF
又BM=MD
∴△EDM≌△FBM
∴BF=DE=AE,EM=FM
∴--------------4分
延长ED到F,连接AF、MF,则AF为矩形ACFE对角线,所以比经过EC的中点N且AN=NF=EN=NC.
在Rt△BDF中,M是BD的中点,∠B=45°
∴FD=FB
∴FM⊥AB,
∴MN=NA=NF=NC
∴点A、C、F、M都在以N为圆心的圆上
∴∠MNC=2∠DAC
由四边形MACF中,∠MFC=135°
∠FMA=∠ACB=90°
∴∠DAC=45°
∴∠MNC=90°即MN⊥FC-------------------7分
25. (1)又当x=20时,.而原数据都在20~100之间,所以新数据都在60~100
之间, 即满足条件(一),……1分
当 时, ,即y= .∴y随着x的增大而增大,即
时,满足条件(二)
综上可知,当 时,这种变换满足要求;……2分
(2)本题是开放性问题,答案不唯一。若所给出的关系式满足:(a)h≤20;(b)若x=20,100时,
y的对应值m,n能落在60~100之间,则这样的关系式都符合要求。
如取h=20, ,……8分
∵a>0,∴当20≤x≤100时,y随着x的增大…10分
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×802+k=100 ②
由①②解得 , ∴ ……8分
A
O
D
B
E
C
J
I
E
C
B
A
H
G
F
D
优秀
良好
及格
各等级人数比
各等级学生平均分数
(图4)
(图3)
(图2)
(图1)
同课章节目录
