苏教版高二下学期数学期末试题(三)含答案
文档属性
| 名称 | 苏教版高二下学期数学期末试题(三)含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 192.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-12 00:00:00 | ||
图片预览




文档简介
苏教版高二下学期数学期末试题(三)
一、填空题
1..若
2.在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的,且样本容量为160,则中间一组的频数为 ▲ .
3.已知是的外心,,若 HYPERLINK "http://www." ,则的值为 ▲ .
4.(满分6分)已知函数对任意的实数,满足且,则 ,此函数为 函数(填奇偶性).
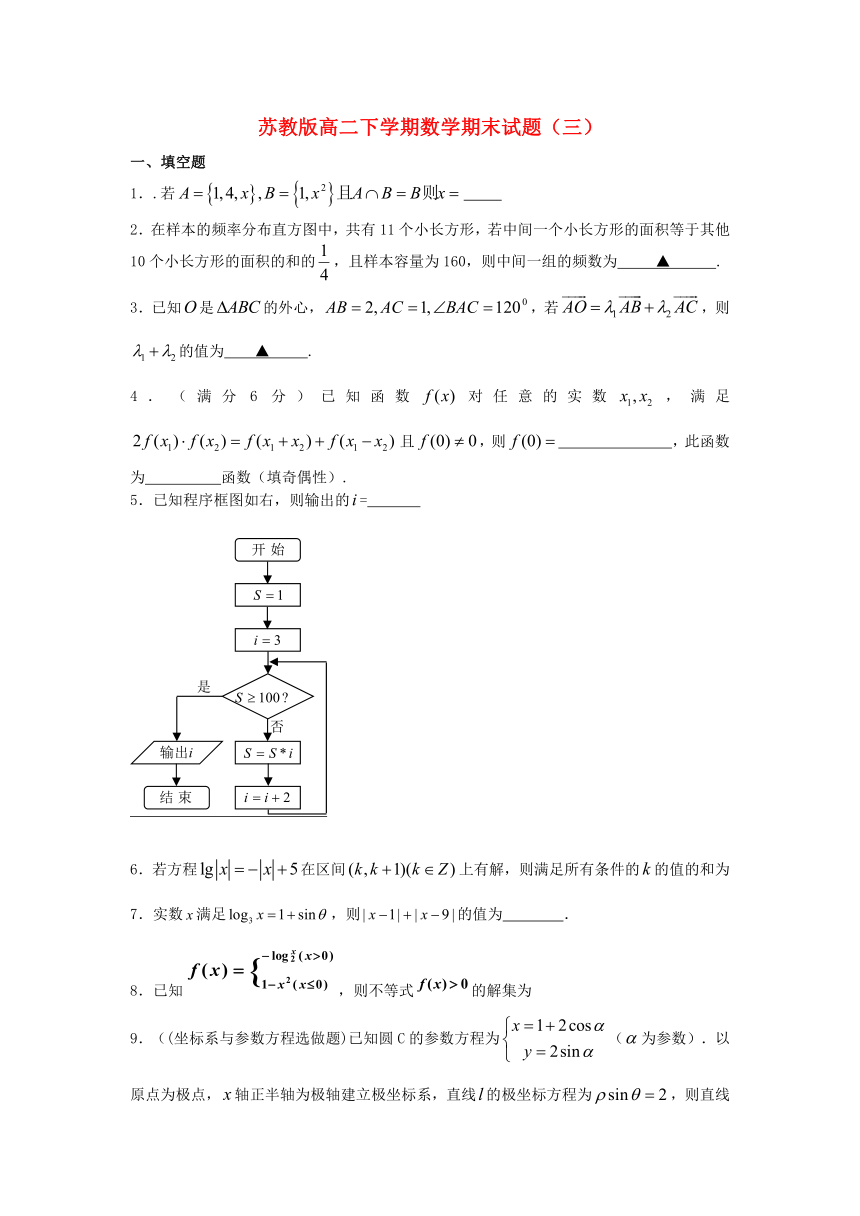
5.已知程序框图如右,则输出的=
6.若方程在区间上有解,则满足所有条件的的值的和为
7.实数满足,则的值为 .
8.已知,则不等式的解集为
9.((坐标系与参数方程选做题)已知圆C的参数方程为(为参数).以原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为,则直线与圆C的公共点的直角坐标为 .
10.已知实数满足 ( http: / / www.21cnjy.com ),若在处取得最小值,则此时__________.
11.在R上定义运算⊙:⊙,则满足⊙的实数的取值范围是__________.
12.在△ABC中,∠BAC=90°,AB=6,D为斜边BC的中点,则的值为__________.
13.已知函数,则该函数的值域为__________.
14. 把数列的所有项按照从大到小,左大右小的原则写成如图所示的数表,第行有个数,第行的第个数(从左数起)记为,则可记为_________.
( http: / / www.21cnjy.com )
二、解答题
15.袋中装有大小相同标号不同的白球4个,黑球5个,从中任取3个球.
(1)共有多少种不同结果?
(2)取出的3球中有2个白球,1个黑球的结果有几个?
(3)取出的3球中至少有2个白球的结果有几个?
(4)计算第(2)、(3)小题表示的事件的概率
16.求证:
17.如图,P是边长为1的正六边形ABCDEF所在平面外一点,,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明⊥;
(Ⅱ)求面与面所成二面角的大小。
18.若数列,其中T为正整数,则称数列为周期数列,其中T为数列的周期。
(I)设是周期为7的数列,其中;
(II)设是周期为7的数列,其中,对(I)中的数列的最小值。
19.已知函数.
(Ⅰ)当时,求函数在,上的最大值、最小值;
(Ⅱ)令,若在上单调递增,求实数的取值范围.
20.中华人民共和国《道路交通安全法》中 ( http: / / www.21cnjy.com )将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).
( http: / / www.21cnjy.com )
(1) 求此次拦查中醉酒驾车的人数;
(2) 从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,
再从抽取的8人中任取3人,求3人中含有醉酒驾车人数x的分布列和期望.
参考答案
1.0 ,-2 ,2
2. 32
3.
4.1;偶函数
5.9
6.
7.8.
8.(-1,1)
9.
10.(-1,0)
11.(-2,1)
12.18
13.
14.(10,495)
15.(1)设从4个白球,5个黑球中任取3个的所有结果组成的集合为I.
∴card(I)=C.
∴共有C=84个不同结果.
(2)设事件:“取出3球中有2个白球,1个黑球”的所有结果组成的集合为A.
∴card(A)=CC.
∴共有CC=30种不同的结果.
(3)设事件:“取出3球中至少有2个白球”的所有结果组成集合为B.
∴card(B)=C+CC.
∴共有C+CC=34种不同的结果.
(4)∵从4个白球,5个黑球中,任取3个球的所有结果的出现可能性都相同,
∴第(2)小题的事件发生的概率为=,
第(3)小题的事件发生的概率为=.
16.证明:
∵∴展开式至少有4项,
∴.
17.解(Ⅰ)在正六边形ABCDEF中,为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;
∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,
∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;
又∵正六边形ABCDEF的边长为1,
∴,,。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,
所以为所求二面角平面角。
在中,OH=,=。
在中,;
而
18.(Ⅰ),,.
……………………3分
(Ⅱ),,.
当时, ①
②
①—②
得
由知,,
,所以满足的的最小值为.
( http: / / www.21cnjy.com )
考察的对称轴为
当,即时,应有
解得:,所以时成立…………9分
当,即时,应有即:
解得…………11分
综上:实数的取值范围是
20.解:(1) (0.032+0.043+0.050)×20=0.25,0.25×60=15,
所以此次拦查中醉酒驾车的人数为15人.…………………………………………………4分
(2) 易知利用分层抽样抽取8人中含有醉酒驾车者为2人;所以x的所有可能取值为0,1,2;
P(x=0)==,P(X=1)==,P(x=2)==
X的分布列为
0 1 2
…………………………………………………………………………………………………10分
.……………………………………………………12分.
A
B
C
D
E
F
O
P
第19题图
H
一、填空题
1..若
2.在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的,且样本容量为160,则中间一组的频数为 ▲ .
3.已知是的外心,,若 HYPERLINK "http://www." ,则的值为 ▲ .
4.(满分6分)已知函数对任意的实数,满足且,则 ,此函数为 函数(填奇偶性).
5.已知程序框图如右,则输出的=
6.若方程在区间上有解,则满足所有条件的的值的和为
7.实数满足,则的值为 .
8.已知,则不等式的解集为
9.((坐标系与参数方程选做题)已知圆C的参数方程为(为参数).以原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为,则直线与圆C的公共点的直角坐标为 .
10.已知实数满足 ( http: / / www.21cnjy.com ),若在处取得最小值,则此时__________.
11.在R上定义运算⊙:⊙,则满足⊙的实数的取值范围是__________.
12.在△ABC中,∠BAC=90°,AB=6,D为斜边BC的中点,则的值为__________.
13.已知函数,则该函数的值域为__________.
14. 把数列的所有项按照从大到小,左大右小的原则写成如图所示的数表,第行有个数,第行的第个数(从左数起)记为,则可记为_________.
( http: / / www.21cnjy.com )
二、解答题
15.袋中装有大小相同标号不同的白球4个,黑球5个,从中任取3个球.
(1)共有多少种不同结果?
(2)取出的3球中有2个白球,1个黑球的结果有几个?
(3)取出的3球中至少有2个白球的结果有几个?
(4)计算第(2)、(3)小题表示的事件的概率
16.求证:
17.如图,P是边长为1的正六边形ABCDEF所在平面外一点,,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明⊥;
(Ⅱ)求面与面所成二面角的大小。
18.若数列,其中T为正整数,则称数列为周期数列,其中T为数列的周期。
(I)设是周期为7的数列,其中;
(II)设是周期为7的数列,其中,对(I)中的数列的最小值。
19.已知函数.
(Ⅰ)当时,求函数在,上的最大值、最小值;
(Ⅱ)令,若在上单调递增,求实数的取值范围.
20.中华人民共和国《道路交通安全法》中 ( http: / / www.21cnjy.com )将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).
( http: / / www.21cnjy.com )
(1) 求此次拦查中醉酒驾车的人数;
(2) 从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,
再从抽取的8人中任取3人,求3人中含有醉酒驾车人数x的分布列和期望.
参考答案
1.0 ,-2 ,2
2. 32
3.
4.1;偶函数
5.9
6.
7.8.
8.(-1,1)
9.
10.(-1,0)
11.(-2,1)
12.18
13.
14.(10,495)
15.(1)设从4个白球,5个黑球中任取3个的所有结果组成的集合为I.
∴card(I)=C.
∴共有C=84个不同结果.
(2)设事件:“取出3球中有2个白球,1个黑球”的所有结果组成的集合为A.
∴card(A)=CC.
∴共有CC=30种不同的结果.
(3)设事件:“取出3球中至少有2个白球”的所有结果组成集合为B.
∴card(B)=C+CC.
∴共有C+CC=34种不同的结果.
(4)∵从4个白球,5个黑球中,任取3个球的所有结果的出现可能性都相同,
∴第(2)小题的事件发生的概率为=,
第(3)小题的事件发生的概率为=.
16.证明:
∵∴展开式至少有4项,
∴.
17.解(Ⅰ)在正六边形ABCDEF中,为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;
∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,
∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;
又∵正六边形ABCDEF的边长为1,
∴,,。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,
所以为所求二面角平面角。
在中,OH=,=。
在中,;
而
18.(Ⅰ),,.
……………………3分
(Ⅱ),,.
当时, ①
②
①—②
得
由知,,
,所以满足的的最小值为.
( http: / / www.21cnjy.com )
考察的对称轴为
当,即时,应有
解得:,所以时成立…………9分
当,即时,应有即:
解得…………11分
综上:实数的取值范围是
20.解:(1) (0.032+0.043+0.050)×20=0.25,0.25×60=15,
所以此次拦查中醉酒驾车的人数为15人.…………………………………………………4分
(2) 易知利用分层抽样抽取8人中含有醉酒驾车者为2人;所以x的所有可能取值为0,1,2;
P(x=0)==,P(X=1)==,P(x=2)==
X的分布列为
0 1 2
…………………………………………………………………………………………………10分
.……………………………………………………12分.
A
B
C
D
E
F
O
P
第19题图
H
同课章节目录
