《数轴与相反数》的自学内容(浙江省台州市路桥区)
文档属性
| 名称 | 《数轴与相反数》的自学内容(浙江省台州市路桥区) |

|
|
| 格式 | rar | ||
| 文件大小 | 43.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-12 00:00:00 | ||
图片预览



文档简介
一. 本周教学内容:
数轴、相反数
[教学目的]
1. 使学生掌握数轴的定义、画法及作用,会利用数轴比较有理数的大小。
2. 使学生掌握相反数的概念、特性及表示方法。
二. 重点、难点:
1. 数轴的概念及三要素,有理数与数轴上的点的对应关系。
2. 相反数的概念及意义,会求一个数的相反数。
三. 教学过程:
(一)本周知识考点分析
1. 数轴的定义:规定了原点、正方向和单位长度的直线叫做数轴。其中原点、单位长度、正方向是数轴三要素,缺一不可。
2. 数轴的画法及作用:
(1)画一条水平直线,在直线上取一点O(叫做原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,得到了数轴。
(2)学习数轴以后,任何一个有理数都可以用数轴上的一个点来表示。原点表示数0,正数在原点的右方,负数在原点的左方。
这里有理数与它对应的数轴上的点体现了数与形的结合。
3. 利用数轴比较有理数的大小:
(1)在数轴上表示的两个数中,右边的数总比左边的数大,正数都大于0,负数都小于0,正数大于一切负数,借助数轴可以比较有理数的大小。
(2)因为正数都大于0,反过来,大于0的数都是正数。
所以可用字母,表示a是正数。反之,a是正数,用表示。
同理:表示a是负数,反之,a是负数,则;
表示a是非负数,反之,a是非负数,则。
4. 相反数的概念:
(1)相反数的几何定义:在数轴上原点的两旁,离开原点的距离相等的两个点表示的数,叫做互为相反数。
例如:如下图所示:与,与
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
(2)相反数的代数定义:
只有符号不同的两个数叫做互为相反数。
特别地:0的相反数是0,也只有0的相反数是它本身。
(3)相反数的特性及表示方法:
①若a、b互为相反数,则。
反之若,则a、b互为相反数。
②一般地,数a的相反数是,这里a表示任意一个数,可以是正数、负数或零,a还可以表示一个任意代数式。
例:若,则,5与互为相反数。
若,则,0的相反数是0。
若,则与38互为相反数。
若,则,与互为相反数。
实际上:求一个数的相反数只需在它前面添上一个负号即可。
(4)多重符号的化简:
①在一个数的前面添加一个“+”号,仍然与原数相同。
如:+8=8
②在一个数的前面添加一个“-”号,就成为原来的相反数,如就是求的相反数。
所以
【典型例题】
例1. 下列各图中,是数轴的是( )
分析:A. 缺少方向,B. 缺少单位,C. 单位不统一。
对照数轴的定义,三个要素缺一不可,故选D。
例2. 在数轴上表示下列各数,并用“<”把它们连接起来。
分析:要想在数轴上准确地描出各点,首先要正确画出数轴,然后注意数的符号,表示负数的点描在原点的左侧,表示正数的点描在原点的右侧,再根据各数值定出的位置,表示0的点就是原点,再根据“在数轴上的点表示的两个数右边的总比左边的大”写出不等式。
解:
注意:画出一个数所对应的点时,把点画成一个黑圆点,以免与刻度线相混淆。
例3. 的相反数是__________,的倒数是__________。
分析:解决的关键是明确相反数,倒数的定义。
解:的相反数是,倒数是。
例4. 化简下列各数的符号。
(1) (2)
分析:利用多重符号化简的方法。
解:
例5. 若与互为相反数,求x的值。
分析:任何一个有理数都有相反数,且只有一个相反数,可以用或来表示。
与互为相反数,则为5或来解决。
解:
或
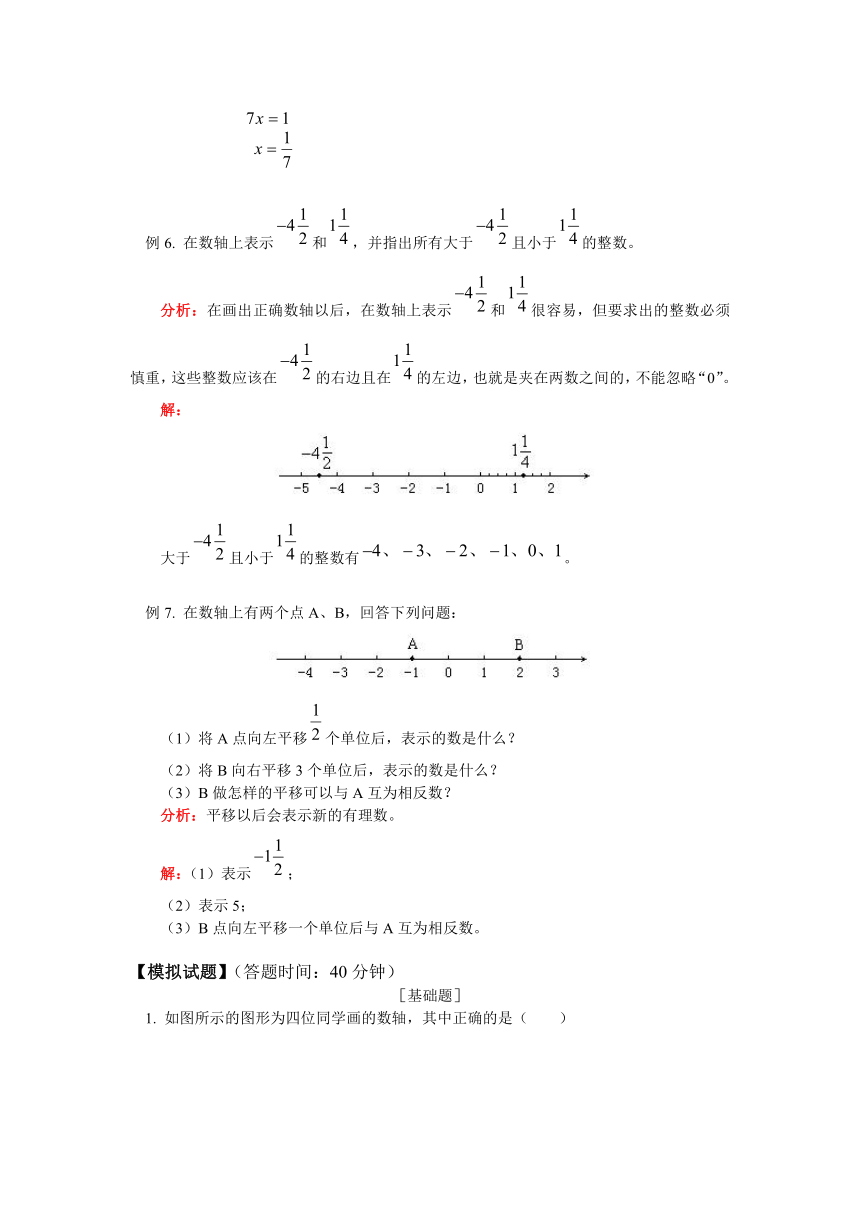
例6. 在数轴上表示和,并指出所有大于且小于的整数。
分析:在画出正确数轴以后,在数轴上表示和很容易,但要求出的整数必须慎重,这些整数应该在的右边且在的左边,也就是夹在两数之间的,不能忽略“0”。
解:
大于且小于的整数有。
例7. 在数轴上有两个点A、B,回答下列问题:
(1)将A点向左平移个单位后,表示的数是什么?
(2)将B向右平移3个单位后,表示的数是什么?
(3)B做怎样的平移可以与A互为相反数?
分析:平移以后会表示新的有理数。
解:(1)表示;
(2)表示5;
(3)B点向左平移一个单位后与A互为相反数。
【模拟试题】(答题时间:40分钟)
[基础题]
1. 如图所示的图形为四位同学画的数轴,其中正确的是( )
2. 如图所示,点M表示的数是( )
A. 2.5 B. C. D. 1.5
3. 下列说法正确的是( )
A. 有原点、正方向的直线是数轴
B. 数轴上两个不同的点可以表示同一个有理数
C. 有些有理数不能在数轴上表示出来
D. 任何一个有理数都可以用数轴上的点表示
4. 下列各组数中,大小关系正确的是( )
A. B.
C. D.
5. 数轴上原点及原点右边的点表示的数是( )
A. 正数 B. 负数 C. 非负数 D. 非正数
6. 数轴上点M到原点的距离是5,则点M表示的数是( )
A. 5 B. C. 5或 D. 不能确定
7. 在数轴上表示的点中,在原点右边的点有( )
A. 0个 B. 1个 C. 2个 D. 3个
8. 最大的负整数是___________;小于3的非负整数有______________________。
9. 若,则x的整数值有___________个。
10. 从数轴上表示的点开始,向右移动6个单位长度,再向左移动5个单位长度,最后到达的终点所表示的数是___________。
11. 在数轴上表示下列各数,并用“<”连接起来。
12. 数轴上与原点的距离是6的点有___________个,这些点表示的数是___________;与原点的距离是9的点有___________个,这些点表示的数是___________。
13. 12的相反数是___________;___________的相反数是。
14. 如果一个数的相反数是负数,那么这个数一定是( )
A. 正数 B. 负数 C. 零 D. 正数、负数或零
15. __________的相反数是它本身。
16. 一个数的相反数是非负数,这个数一定是( )
A. 正数或零 B. 非零的数
C. 负数或零 D. 零
17. 下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 与2.75都是的相反数
D. 0没有相反数
18. 在数轴上点A、B分别表示和,则数轴上与A、B两点的距离相等的点表示的数是___________。
19. 的意义是___________,的意义是___________。
20. 在数轴上表示出各数及它们的相反数。
21. 化简下列各数:
[探究应用题]
22. (应用题)
小明在A地东15米,他走了15米,结果离A地还有30米,这是怎么回事?
23. (创新题)
数轴上表示整数的点称为整点。某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2004厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2002或2003 B. 2003或2004
C. 2004或2005 D. 2005或2006
24. (易错题)
与的大小关系有三种:①>;②=;③<。请举例说明。
25. (综合题)
已知与互为相反数,求m的值。
26. 若向东走8米,记作米,如果一个人从A地出发向东走12米,再走米,又走了米,你能判断此人这时在何处吗?
【试题答案】
[基础题]
1. D 2. C 3. D 4. A 5. C 6. C 7. C
8.
9. 6。分别为-2,-1,0,1,2,3
10. 0
11. 图略,
12. 两个,6和;两个,9或
13.
14. A 15. 0 16. C
17. C 18. 0
19. 的相反数;本身
20. 图略
21.
[探究应用题]
22. 小明向东走了15米
23. C
若线段AB的端点与整点重合,则线段AB盖住2005个点;若端点不与整点重合,则AB盖住2004个点。
24. 时,;
;
时,
25. 或,
26. 此人这时在A地东13米处
【励志故事】
用进废退
意大利小男孩托蒂有一只十分奇怪的眼睛。说“十分奇怪”,主要是因为眼科大夫多次会诊得出的结论都相同:从生理上看,这是一只完全正常的眼睛。但是这只眼睛却是失明的。一只完全正常的眼睛何以失明了呢?原来,当小托蒂呱呱坠地时,由于这只眼睛轻度感染,曾被绷带缠了两个星期,正是这种对常人来说几乎没有任何副作用的治疗,对刚刚出生、大脑正处于构建发育关键期的婴儿托蒂造成了极大的伤害。他的大脑由于长时间无法从这只眼睛接受任何外界信息,就认为它瞎了,于是原先该为它工作的大脑神经组织也随之“战略转移”了。
小托蒂遭遇的不幸并非偶然性的特殊个案。后来,研究人员在动物身上做了很多类似的实验,发现结果都是一样的,都严格执行着“用进废退”的规则。
数轴、相反数
[教学目的]
1. 使学生掌握数轴的定义、画法及作用,会利用数轴比较有理数的大小。
2. 使学生掌握相反数的概念、特性及表示方法。
二. 重点、难点:
1. 数轴的概念及三要素,有理数与数轴上的点的对应关系。
2. 相反数的概念及意义,会求一个数的相反数。
三. 教学过程:
(一)本周知识考点分析
1. 数轴的定义:规定了原点、正方向和单位长度的直线叫做数轴。其中原点、单位长度、正方向是数轴三要素,缺一不可。
2. 数轴的画法及作用:
(1)画一条水平直线,在直线上取一点O(叫做原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,得到了数轴。
(2)学习数轴以后,任何一个有理数都可以用数轴上的一个点来表示。原点表示数0,正数在原点的右方,负数在原点的左方。
这里有理数与它对应的数轴上的点体现了数与形的结合。
3. 利用数轴比较有理数的大小:
(1)在数轴上表示的两个数中,右边的数总比左边的数大,正数都大于0,负数都小于0,正数大于一切负数,借助数轴可以比较有理数的大小。
(2)因为正数都大于0,反过来,大于0的数都是正数。
所以可用字母,表示a是正数。反之,a是正数,用表示。
同理:表示a是负数,反之,a是负数,则;
表示a是非负数,反之,a是非负数,则。
4. 相反数的概念:
(1)相反数的几何定义:在数轴上原点的两旁,离开原点的距离相等的两个点表示的数,叫做互为相反数。
例如:如下图所示:与,与
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
(2)相反数的代数定义:
只有符号不同的两个数叫做互为相反数。
特别地:0的相反数是0,也只有0的相反数是它本身。
(3)相反数的特性及表示方法:
①若a、b互为相反数,则。
反之若,则a、b互为相反数。
②一般地,数a的相反数是,这里a表示任意一个数,可以是正数、负数或零,a还可以表示一个任意代数式。
例:若,则,5与互为相反数。
若,则,0的相反数是0。
若,则与38互为相反数。
若,则,与互为相反数。
实际上:求一个数的相反数只需在它前面添上一个负号即可。
(4)多重符号的化简:
①在一个数的前面添加一个“+”号,仍然与原数相同。
如:+8=8
②在一个数的前面添加一个“-”号,就成为原来的相反数,如就是求的相反数。
所以
【典型例题】
例1. 下列各图中,是数轴的是( )
分析:A. 缺少方向,B. 缺少单位,C. 单位不统一。
对照数轴的定义,三个要素缺一不可,故选D。
例2. 在数轴上表示下列各数,并用“<”把它们连接起来。
分析:要想在数轴上准确地描出各点,首先要正确画出数轴,然后注意数的符号,表示负数的点描在原点的左侧,表示正数的点描在原点的右侧,再根据各数值定出的位置,表示0的点就是原点,再根据“在数轴上的点表示的两个数右边的总比左边的大”写出不等式。
解:
注意:画出一个数所对应的点时,把点画成一个黑圆点,以免与刻度线相混淆。
例3. 的相反数是__________,的倒数是__________。
分析:解决的关键是明确相反数,倒数的定义。
解:的相反数是,倒数是。
例4. 化简下列各数的符号。
(1) (2)
分析:利用多重符号化简的方法。
解:
例5. 若与互为相反数,求x的值。
分析:任何一个有理数都有相反数,且只有一个相反数,可以用或来表示。
与互为相反数,则为5或来解决。
解:
或
例6. 在数轴上表示和,并指出所有大于且小于的整数。
分析:在画出正确数轴以后,在数轴上表示和很容易,但要求出的整数必须慎重,这些整数应该在的右边且在的左边,也就是夹在两数之间的,不能忽略“0”。
解:
大于且小于的整数有。
例7. 在数轴上有两个点A、B,回答下列问题:
(1)将A点向左平移个单位后,表示的数是什么?
(2)将B向右平移3个单位后,表示的数是什么?
(3)B做怎样的平移可以与A互为相反数?
分析:平移以后会表示新的有理数。
解:(1)表示;
(2)表示5;
(3)B点向左平移一个单位后与A互为相反数。
【模拟试题】(答题时间:40分钟)
[基础题]
1. 如图所示的图形为四位同学画的数轴,其中正确的是( )
2. 如图所示,点M表示的数是( )
A. 2.5 B. C. D. 1.5
3. 下列说法正确的是( )
A. 有原点、正方向的直线是数轴
B. 数轴上两个不同的点可以表示同一个有理数
C. 有些有理数不能在数轴上表示出来
D. 任何一个有理数都可以用数轴上的点表示
4. 下列各组数中,大小关系正确的是( )
A. B.
C. D.
5. 数轴上原点及原点右边的点表示的数是( )
A. 正数 B. 负数 C. 非负数 D. 非正数
6. 数轴上点M到原点的距离是5,则点M表示的数是( )
A. 5 B. C. 5或 D. 不能确定
7. 在数轴上表示的点中,在原点右边的点有( )
A. 0个 B. 1个 C. 2个 D. 3个
8. 最大的负整数是___________;小于3的非负整数有______________________。
9. 若,则x的整数值有___________个。
10. 从数轴上表示的点开始,向右移动6个单位长度,再向左移动5个单位长度,最后到达的终点所表示的数是___________。
11. 在数轴上表示下列各数,并用“<”连接起来。
12. 数轴上与原点的距离是6的点有___________个,这些点表示的数是___________;与原点的距离是9的点有___________个,这些点表示的数是___________。
13. 12的相反数是___________;___________的相反数是。
14. 如果一个数的相反数是负数,那么这个数一定是( )
A. 正数 B. 负数 C. 零 D. 正数、负数或零
15. __________的相反数是它本身。
16. 一个数的相反数是非负数,这个数一定是( )
A. 正数或零 B. 非零的数
C. 负数或零 D. 零
17. 下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 与2.75都是的相反数
D. 0没有相反数
18. 在数轴上点A、B分别表示和,则数轴上与A、B两点的距离相等的点表示的数是___________。
19. 的意义是___________,的意义是___________。
20. 在数轴上表示出各数及它们的相反数。
21. 化简下列各数:
[探究应用题]
22. (应用题)
小明在A地东15米,他走了15米,结果离A地还有30米,这是怎么回事?
23. (创新题)
数轴上表示整数的点称为整点。某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2004厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2002或2003 B. 2003或2004
C. 2004或2005 D. 2005或2006
24. (易错题)
与的大小关系有三种:①>;②=;③<。请举例说明。
25. (综合题)
已知与互为相反数,求m的值。
26. 若向东走8米,记作米,如果一个人从A地出发向东走12米,再走米,又走了米,你能判断此人这时在何处吗?
【试题答案】
[基础题]
1. D 2. C 3. D 4. A 5. C 6. C 7. C
8.
9. 6。分别为-2,-1,0,1,2,3
10. 0
11. 图略,
12. 两个,6和;两个,9或
13.
14. A 15. 0 16. C
17. C 18. 0
19. 的相反数;本身
20. 图略
21.
[探究应用题]
22. 小明向东走了15米
23. C
若线段AB的端点与整点重合,则线段AB盖住2005个点;若端点不与整点重合,则AB盖住2004个点。
24. 时,;
;
时,
25. 或,
26. 此人这时在A地东13米处
【励志故事】
用进废退
意大利小男孩托蒂有一只十分奇怪的眼睛。说“十分奇怪”,主要是因为眼科大夫多次会诊得出的结论都相同:从生理上看,这是一只完全正常的眼睛。但是这只眼睛却是失明的。一只完全正常的眼睛何以失明了呢?原来,当小托蒂呱呱坠地时,由于这只眼睛轻度感染,曾被绷带缠了两个星期,正是这种对常人来说几乎没有任何副作用的治疗,对刚刚出生、大脑正处于构建发育关键期的婴儿托蒂造成了极大的伤害。他的大脑由于长时间无法从这只眼睛接受任何外界信息,就认为它瞎了,于是原先该为它工作的大脑神经组织也随之“战略转移”了。
小托蒂遭遇的不幸并非偶然性的特殊个案。后来,研究人员在动物身上做了很多类似的实验,发现结果都是一样的,都严格执行着“用进废退”的规则。
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
